Конспект урока о геометрии "Введение в стереометрию" 10 класс.

Конспект урока

Геометрия, 10 класс

Урок №3. Введение в стереометрию

Перечень вопросов, рассматриваемых в теме

1.     определение стереометрии;

2.     понятие пространства;

3.     аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве, а также следствия из них.

Глоссарий по теме

Геометрия- это наука о свойствах геометрических фигур.

Планиметрия- это раздел геометрии, в котором изучаются свойства фигур на плоскости.

Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.

Обязательная литература:

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии. 10 кл. Москва.: Просвещение, 2013 г. С. 1-4

Дополнительная литература:

Зив Б. Г. Геометрия. 10 класс. Дидактические материалы.: Москва, Просвещение, 2013 г. С.4, 14, 24

Открытый электронный ресурс:

Решу ЕГЭ. Открытый образовательный портал. https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Мы закончили изучать и повторять раздел геометрии, который называется планиметрией.

В планиметрии все фигуры, которые рассматривались при доказательстве каждой теоремы или при решении задач, располагались на плоскости. Таким образом, мы имели дело только с одной плоскостью.

Сегодня мы начинаем изучать новый раздел геометрии, который называется стереометрией.

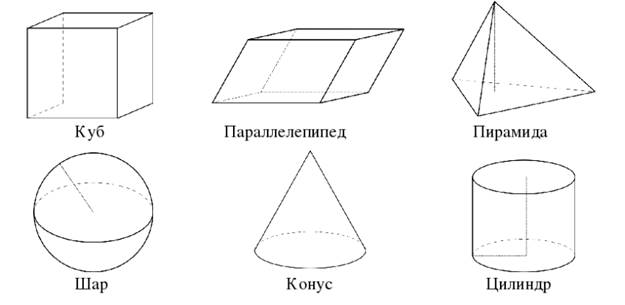
Обратите внимание на данные фигуры. Как вы заметили- они объемные.

И их все объединяет раздел геометрии Стереометрия.

Что же такое стереометрия?

По аналогии с планиметрией мы можем вывести следующее определение:

Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.

Вместе с этими фигурами рассматриваются геометрические тела и их поверхности. Представления о геометрических телах дают нам: кристаллы (составлен из многоугольников) – многогранники; куб; капли жидкости в невесомости – шар; футбольный мяч (шар); консервная банка (цилиндр).

Многогранники:

Куб:

Шар:

Цилиндр:

Изучая свойства геометрических фигур, мы получаем представления о геометрических свойствах реальных предметов. В этом и состоит практическое значение геометрии, в частности стереометрия, широко используется в строительстве, архитектуре, машиностроении, геодезии, в науке и технике.

В планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается ещё одна основная фигура – плоскость.

Представление плоскости нам дает любая гладкая поверхность. Она безгранична.

В стереометрии:

1.     точки обозначаются прописными латинскими буквами: А, В, С и т. д.

2.     прямые – строчными латинскими буквами: а, b, с и т. д. или двумя большими латинскими буквами: АВ, ВС и т. д.

3.     плоскости – греческими буквами: α, β, γ и т. д.

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.

А1: Через 3 точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

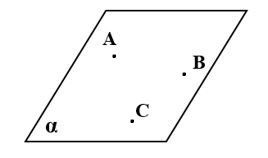
Точки А  α, В  α, С  α.

Если взять четыре произвольные точки, то через них может не проходить ни одна плоскость.

А2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.

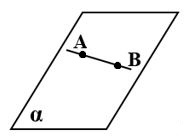
Это свойство используется при проверке “ровности” линейки.

Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.

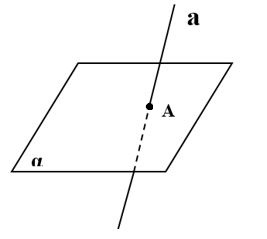
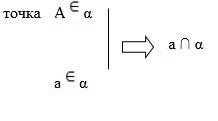
А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае говорят, что плоскости пересекаются по прямой.

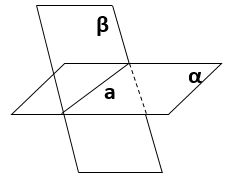
Пример: пересечение пола и стены

В пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии.

Некоторые следствия из аксиом.

Теорема 1: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Дано: а – прямая, точка М ∉ а.

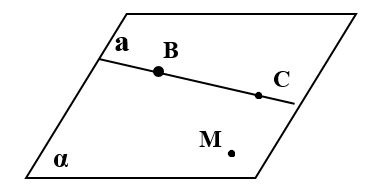
Доказать: 1) существует α: а  α.

2) α – единственная.

Доказательство:

1) Дополнительные построения: т. В  а, т. С а.

2) В, С, М не лежат на одной прямой, следовательно, по первой аксиоме существует плоскость α.

3) т. к.

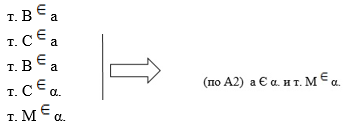
4) Единственность α. следует из того, что любая плоскость, проходящая через прямую а и т. М, проходит через М, В, С. Значит, она совпадает с α (по Аксиоме 1). Теорема доказана.

Теорема 2: Через две пересекающиеся прямые проходит плоскость, и, причём только одна.

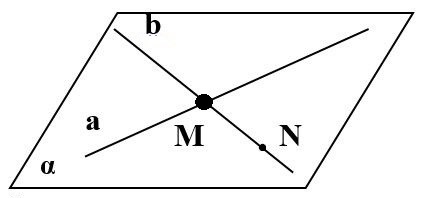
Дано: а ∩ b в точке М

Доказать: существование плоскости α, а α, b  α.

Доказательство:

1) Дополнительные построения: N Є b, N∉ a.

2) Существует α : N  α, a  α.

3) 

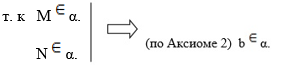
4) Из 2) и 3) следует α. проходит через прямые а и b.

5) Единственность α следует из того, что любая плоскость, проходящая через прямые а и b, проходит через точку N, значит она совпадает с α (по Теореме 1). Теорема доказана.

Разбор решения заданий тренировочного модуля

№1.

Тип задания: выделение цветом

Прямая MN пересекает плоскость:

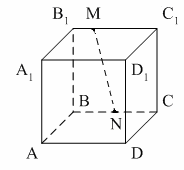
1) (АА₁В₁);

2) (ABC);

3) (AA₁D₁).

Разбор решения:

Внимательно рассмотрите рисунок, как вы видите прямая MN пересекает плоскости ABC и A₁B₁С_1, рассмотрим варианты ответов, среди них есть вариант 2) (ABC), он и является верным.

Ответ: 2) (ABC);

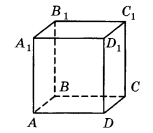
№2.

Тип задания: смежный граф

Пользуясь данным рисунком

назовите три плоскости, содержащие прямую DС₁ (нижний индекс записываете цифрой после буквы, без пробела)

Решение: Внимательно рассмотрите прилагающийся рисунок, определите, где на нем располагается прямая DС₁, как вы видите из рисунка он располагается в плоскостях:

1)DD₁С₁С

2)D₁С₁С

3) DСС₁

Их и запишем в ответ.

Ответ: 1)DD₁С₁С; 2)D₁С₁С; 3) DСС₁

Скачано с www.znanio.ru