Конспект урока "Освобождение от иррациональности в знаменателе" 8 класс

Урок № 40                     8.12                 8 кл

Тема урока : «Освобождение от иррациональности в знаменателе »

Учителя Шимек Н.В.

Цели урока :

- Повторить преобразование выражений, содержащих квадратный корень, с

использованием формул сокращенного умножения.

-  Выработать алгоритм освобождения от иррациональности в знаменателе

дроби.

-  Сформировать у учащихся навыки применения этого алгоритма при

преобразовании выражений, содержащих иррациональность в знаменателе

дроби.

Результаты:

Предметные: формировать умение преобразовывать выражения, содержащие арифметические квадратные корни, освобождать дробь от иррациональности в знаменателе.

Личностные: формировать устойчивый познавательный интерес; умение ясно, точно, грамотно излагать и обосновывать свои мысли в устной речи.

Метапредметные: формировать умение корректировать свои действия при решении упражнений.

Планируемые результаты: учащиеся научатся преобразовывать выражения, содержащие арифметические квадратные корни, освобождать дробь от иррациональности в знаменателе.

Тип урока: комбинированный

Оборудование: тетрадь, раздаточный материал, мультимедийная доска

 

                                     

Ход урока

1. Орг.момент 

Приветствие, записать число, кл работа, отметить отсутствующих

 Добрый день, ребята!

- Проверьте все ли у вас готово  к уроку.
- Готовы к уроку? Итак, начинаем.

 

2. Постановка темы, цели, задачи

 

3. Актуализация опорных знаний

n  Что называют арифметическим квадратным корнем из числа а?

 

n  Как найти квадратный корень из произведения, дроби?

 

n  При каком а выражение       имеет смысл?

 

n  Чему равен      ?

 

n  Чему равно ?

 

Вычисли:

 

 

 

 

 

 

 

 

Какие алгебраические формулы вы применяли? (формула разности квадратов)

 

 

Задания в группах: Подбери недостающий множитель так , чтобы результат не содержал знака квадратного корня

 

 

4. Изучение нового материала

 

 

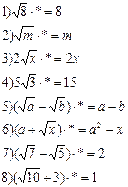
Что проще вычислить?

 

 

Почему верно равенство?

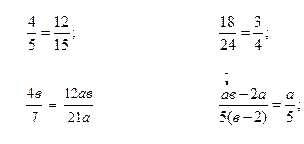
Задача. Преобразовать алгебраическое выражение к такому виду, чтобы знаменатель дроби не содержал знаков квадратных корней

Решение.

Используем основное свойство дроби, то есть подбираем такой множитель, чтобы при умножении на него в знаменателе дроби не оказалось квадратных корней.

Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют освобождением от иррациональности в знаменателе. (слайд 8)

Алгоритм освобождения от иррациональности в знаменателе дроби:

1. Разложить знаменатель дроби на множители.
2. Если знаменатель имеет вид или содержит множитель , то числитель и знаменатель следует умножить на . Если знаменатель имеет вид  , то числитель и знаменатель дроби надо умножить на выражение, сопряженное знаменателю.
3. преобразовать числитель и знаменатель дроби , если возможно, то сократить полученную дробь.

Выражения вида и  называются сопряженными.

 

5.     Самостоятельная работа

Задание 1. Освободите выражение от иррациональности в знаменателе.

Умение освобождаться от иррациональности в знаменателе во многих случаях облегчает тождественные преобразования выражений.

6.Творческое задание

n  Мартышка – апельсинов продавщица,

n  Приехав как – то раз к себе на дачу,

n  Нашла там с радикалами задачу.

n  Но сосчитать не в силах стройный ряд,

n  Разбрасывать их стала все подряд.

n  И молвила: « Что толку в той задаче

n  Коль из нее не слепишь новой дачи!»

n  Мы верим все же, что мартышки мненье –

n  Не истинно для тех, кто знает толк ученье

n  И просим вас, девчонки и мальчишки,

n  Решить задачу на хвосте мартышки.

 

 

7. Итог урока. Рефлексия

- Каким алгоритмом мы можем для этого воспользоваться?

- С какими трудностями столкнулись на уроке?

- Какие оценки вы поставите друг другу за урок?

8.Домашнее задание

 №504

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вычисли:

 

 

 

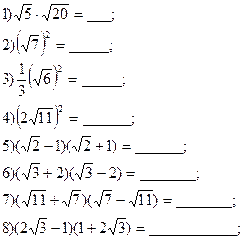
Подбери недостающий множитель

 

 

 

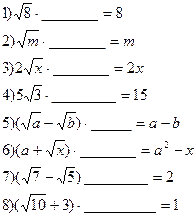
Самостоятельная работа.

Используя алгоритм освобождения от иррациональности в знаменателе дроби решить следующие задания.

Задание 1. Освободите выражение от иррациональности в знаменателе.

 

 

Опорные правила

 

Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют освобождением от иррациональности в знаменателе

 

Алгоритм освобождения от иррациональности в знаменателе дроби:

1Разложить знаменатель дроби на множители.

2  Если знаменатель имеет вид или содержит множитель , то числитель и знаменатель следует умножить на . Если знаменатель имеет вид  , то числитель и знаменатель дроби надо умножить на выражение, сопряженное знаменателю.

a.      преобразовать числитель и знаменатель дроби , если возможно, то сократить полученную дробь.

Выражения вида и  называются сопряженными.