Конспект урока "Перевод чисел из одной системы счисления в другую систему счисления"

 «Перевод чисел из одной системы       счисления в другую»

Тема урока:  «Перевод чисел из одной системы счисления в другую»

(урок закрепления знаний)

Цели урока:

ü Закрепить у учащихся навыки и умения перевода чисел из одной системы счисления в другую систему счисления;

ü Развитие внимания, памяти учащихся; привить навыки самостоятельности в работе, воспитание аккуратности и дисциплинированности.

Учебник: Семакин И.Г. Информатика и ИКТ: учебник для 8 класса / И.Г.Семакин, Л.А.Залогова, С.В.Русаков, Л.В.Шестакова. – М.: БИНОМ. Лаборатория знаний, 2010

Ход урока

I.                  Организационный момент

II.               Проверка домашнего задания (фронтальный опрос)

Учитель задает следующие вопросы учащимся (слайд №1):

1.     Что такое система счисления?

Дети: система счисления – это совокупность правил для обозначения и наименования чисел.

2.     Какие виды систем счисления вы знаете?

Дети: различают два типа систем: позиционные и непозиционные

3.     Чем отличаются позиционные системы от непозиционных?

Дети: в непозиционных системах счисления значение любой цифры не зависит от занимаемой позиции. В позиционных системах счисления значение любой цифры в числе зависит от ее положения в ряду цифр, изображающих это число.

4.     Что называется основанием системы счисления?

основанием системы счисления называется количество знаков используемых для изображения числа в данной системе счисления.

5.     Какое основание имеют двоичная, восьмеричная, десятичная, шестнадцатеричная системы счисления?

2; 8; 10; 16.

6.     Алгоритм перевода чисел из любой системы счисления в десятичную

Алгоритм перевода чисел из любой системы счисления в десятичную:

- Представьте число в развернутой форме. При этом основание системы счисления должно быть представлено в десятичной системе счисления

- Найдите сумму ряда. Полученное число является значением числа в десятичной системе счисления

7.     Алгоритм перевода чисел из десятичной системы счисления в любую другую

Алгоритм перевода целых чисел из десятичной системы счисления в любую другую

- Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.

- Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

- Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

8.     Алгоритм перевода чисел из двоичной системы счисления в системы счисления с основанием 2ⁿ и обратно

Алгоритм перевода целых двоичных чисел в систему счисления с основанием q=2n

Двоичное число разбить справа налево на группы по n в каждой

Если в левой последней группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.

Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2_n

III.           Закрепление изученного материала

Задание №1:

Соедините числа, имеющие равное значение

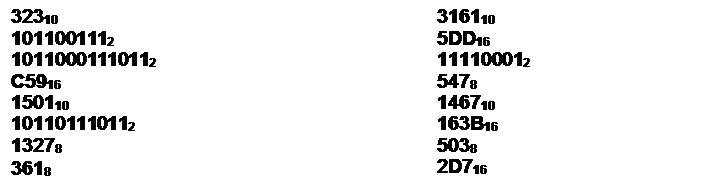
Ответ:  представлен в презентации к конспекту (слайд №2)

Задание № 2:

Разгадайте кроссворд (слайд №3)

Перевести числа из данной системы счисления в указанную систему счисления

По горизонтали:

1.  117₁₀         Х₂

2.  2004₁₀        Х₁₆

5.  3652₈         Х₁₀

6.  6733₁₀        Х₁₆

7.  1101100111₂        Х₈

8.  961₁₆         Х₁₀

9.  23F₁₆         Х₈

10. 11611₈     Х₁₀

11. 4273₁₀       Х₁₆

13. 7049₁₆        Х₈

16. 1111000111000₂       Х₁₆

17. 11101101111₂       Х₁₀

По вертикали:

1. 731₈        Х₁₆

2. 390B1₁₆        Х₈

3. 635D9₁₆        Х₁₀

4. 111101100₂        Х₁₆

5. 263₈        Х₂

8. 4E0149₁₆        Х₈

10. 101000011001₂        Х₈

12. 9E₁₆        Х₂

14. 143₁₀        Х₂

15. FD₁₆        Х₂

18. 22D1₁₆        Х₁₀

Ответы: По горизонтали: 1. 1110101; 2. 7D4; 5. 1962; 6. 1A4D; 7. 1547; 8. 2401; 9. 1077; 10. 5001; 11. 10B1; 13. 70111; 16. 1E38; 17. 1903

               По вертикали: 1. 1D9; 2. 710261; 3. 407001; 4. 1EC; 5. 10110011; 8. 23400511; 10. 5031; 12. 10011110; 14. 10001111; 15. 11111101; 18. 8913

      IV. Итоги урока.

Оцениваю работу класса и называю учащихся, отличившихся на уроке.

Домашнее задание (слайд №4)

1.     Заполните следующую таблицу

Ответы: 1строка: 65; 53; 35

2 строка: 10001111; 143; 8F

3 строка: 100000101; 405; 105

4 строка: 10010101100; 2254; 1196

Список использованной литературы:

1.     Шелепаева А.Х. Поурочные разработки по информатике: 8-9 классы. – М.: ВАКО, 2008. – 272 с. – (В помощь школьному учителю)

2.     Соколова О.Л. Универсальные поурочные разработки по информатике: 10 класс. – М.: ВАКО, 2008. – 400 с. – (В помощь школьному учителю)

3.     Увлекательная информатика. 5-11 классы: логические задачи, кроссворды, ребусы, игры / авт.-сост. Н.А.Владимирова. – Волгоград: Учитель, 2011 – 141 с.