Конспект урока по алгебре 8 класс на тему "Десятичные приближения иррациональных чисел"

Класс__________Дата__________

Урок № ____

ДЕСЯТИЧНЫЕ ПРИБЛИЖЕНИЯ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ

Цели: закрепить знания о понятии иррациональные числа; научиться различать множества иррациональных чисел по отношению к другим числам; находить десятичные приближения рациональных и иррациональных чисел.

Тип урока:  комбинированный

Ход урока:

1. Организационный момент

2. Актуализация знаний

Повторение темы прошлого урока.

Задание: решите уравнения:

3. Изучение нового материала

Мы знаем, что легко найти корень из чисел 4, 9, 25, 64 и так далее. Но тяжело сказать сразу чему равен корень из чисел 2, 3, 5, 7, 13 и т.д. В таких случаях мы используем приближенные значения квадратного корня. Проще всего воспользоваться помощью калькулятора. Чтобы извлечь корень из некоторого числа нужно ввести это число в калькулятор со знаком радикала. На экране высветиться приближенное значение корня. Давайте попробуем извлечь корень из нескольких чисел с помощью калькулятора.

Но бывают случаи, когда калькулятора под рукой нет, тогда мы приходим к самостоятельным расчетам. Рассмотрим следующий случай.

Найдем приближенное значение √3 с двумя знаками после запятой.

Оценим подкоренное выражение 3 сначала в целых числах. Так как 1 < 3 < 4, то √1 < √3 < √4 или 1 < √3 < 2. Поэтому десятичная запись числа √З начинается с цифры 1, т. е. √3 ≈ 1,… (рис. а).

Найдем теперь цифру десятых. Для этого будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3… до тех пор, пока вновь не оценим такими числами подкоренное выражение 3. Имеем 1,1² = 1,21; 1,2² = 1,44; 1,3² = 1,69; 1,4² = 1,96; 1,5² = 2,25; 1,6² = 2,56; 1,7² = 2,89; 1,8² = 3,24. Так как 2,89 < 3 < 3,24 или 1,7² < 3 < 1,8², то 1,7 < √З < 1,8. Значит, √3 ≈ 1,7… (рис. б).

Чтобы найти цифру сотых, будем последовательно возводить в квадрат десятичные дроби 1,71; 1,72; 1,73…, вновь оценивая подкоренное выражение 3. Имеем: 1,71² = 2,9241; 1,72² = 2,9584; 1,73² = 2,9929; 1,74² = 3,0276. Так как 1,73² < 3 < 1,74², то 1,73 < √3 < 1,74 (рис. в). Поэтому √3 ≈ 1,73.

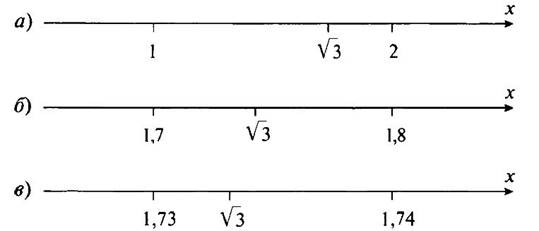
Аналогичным образом можно найти приближенное значение арифметического квадратного корня с любой заданной точностью.

При практических расчетах для нахождения приближенных значений квадратных корней используют специальные таблицы или вычислительную технику.

4. Физкультминутка

5. Формирование умений и навыков

 № 339 (а); 340 (б); 344 (а, б); 345 (а); 348 (б, г).

6. Итоги урока

Домашнее задание: п. 14 изучить, № 345 (б); 348 (а, в).