Конспект урока по алгебре с использованием ИКТ-технологий Тема: "Решение тригонометрических уравнений и неравенств"

Приложение

Конспект  урока по алгебре с использованием ИКТ-технологий

(10 класс)

Тема: "Решение тригонометрических уравнений и неравенств"

Цель: показать возможность применения программных средств к решению тригонометрических уравнений и неравенств; развивать интерес к обучению  и навыки работы за компьютером;  воспитывать культуру математических приемов, вычислительных навыков.

Тип урока: комбинированный

Межпредметные связи: математика – информатика

Оборудование: таблицы, компьютер, учебник.

Ход урока

I.                   Организационный этап

II.                Проверка домашнего задания.

III. Актуализация опорных знаний

1. Решите уравнение: 2sin x=1.

(x=).

2. Установите закономерность и замените знак вопроса выражением:

3. Решите уравнение   с помощью программы «Mathematica 5.0».

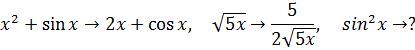
IV. Решение упражнений.

(Класс объединен в группы по 3 учащихся. В каждой группе по 2 аналитика (учащиеся, которые решают задания с помощью математических алгоритмов) и 1 учащийся – практик, который решает задания с использованием компьютером.)

1. Решите уравнение:

Решение:

,

,

,

;

,

;

,

.

Итак, .

(Вместе с учащимися обозначим на единичной окружности множество решений данного уравнения).

2. Решите уравнение   с помощью программы «Mathematica 5.0».

(После решения уравнения на компьютере учащиеся сравнивают полученные решения с множеством, обозначенным на единичной окружности, и убеждаются в том, что уравнение решено верно).

3. Решите неравенство: .

Решение:

Упростим левую часть неравенства и используем метод интервалов.

Итак, .

Найдем нули левой части неравенства: ,

,

;

,

Для решения неравенства достаточно определить знак функции

на промежутке . Из нулей функции данному промежутку принадлежат точки:

0; .

Изобразим решения неравенства на единичной окружности.

Итак,

.

4. Решите неравенство   с помощью программы «GRANI»

 Решение:

Необходимо создать объект с помощью пункта меню Объект→ Создать. Построим график с помощью пункта меню График→ Построить и решаем неравенство с помощью пунктов Операции→ Неравенства→ Система неравенств .

(Анализируем решения, сравнивая их с полученными аналитическим путем)

I.                   Итоги урока

VI. Домашнее задание.

Исследовать и построить график функции . Сравнить его с графиком, полученным при использовании компьютера.