Конспект урока по математике на тему Вычисление площади треугольника(4 класс)

Вычисление площади треугольника

Цели: дать представление о вычислении площади треугольника; учить строить чертеж; формировать умение формулировать правило вычисления площади треугольника; закреплять умения проводить необходимые разбиения и измерения для того, чтобы вычислить площадь каждого закрашенного треугольника.

Ход урока

I. Устный счет.

1. Математический диктант.

а) Представьте в виде суммы произведение 127 ∙  3.

б) Представьте в виде произведения сумму 36 + 36 + 36.

в) Разложите на два равных множителя числа 16 и 81.

г) Найдите значение выражения 18 ∙  х, если х = 0.

д) При каком значении у верно равенство 14 ∙  у = 14?

е) Запишите равенство, выражающее переместительный закон умножения.

ж) Произведение чисел 25 и 248 равно 6200. Чему равно произведение чисел 248 и 25?

2. По столбу высотой 10 м взбирается улитка. За день она поднимается по столбу на 5 метров, за ночь опускается на 4 м. Сколько дней ей потребуется, чтобы подняться на вершину столба?

Решение. За первый день улитка поднимается на 5 м, а за ночь опустится на 4 м. Следовательно, за первые сутки она окажется на высоте 1 м; 5 м пройдет за 5 суток. На шестой день улитка достигнет высоты.

3. Решите задачу. В саду посадили 4 ярда яблонь по 12 яблонь в каждом ряду и 2 ряда слив по 18 слив в каждом ряду. Сколько всего деревьев посадили?

Измените вопрос задачи, чтобы она решалась так: 12 ∙  4 – 18 ∙  2.

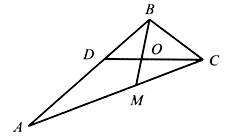
4. Назовите треугольники, у которых одной из вершин является точка А; точка О. Сколько всего треугольников на чертеже?

II. Работа по учебнику.

Задание 389. Начертите равнобедренный  треугольник с основанием 6 см и высотой 4 см. Разбейте этот треугольник на два прямоугольных треугольника. Будут ли эти треугольники равны? (Будут.) Какую  длину  имеют  катеты  этих  треугольников? (4 см и 3 см.) Вычислите площадь такого прямоугольного треугольника. 4 · 3 : 2 = 6 (кв. см). Вычислите площадь исходного равнобедренного треугольника. 6 · 2 = 12 (кв. см). Сравните вычисленную площадь равнобедренного треугольника с площадью прямоугольника со сторонами 6 см и 4 см.

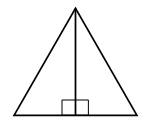
6 · 4 = 24 (кв. см) – площадь прямоугольника со сторонами 6 см и 4 см.

24 : 12 = 2 (раза) – больше площадь прямоугольника, чем площадь равнобедренного треугольника.

Задание 390. Рассмотрите чертеж в учебнике. Проведите в каждом из двух прямоугольников диагонали так, чтобы они имели общую вершину.

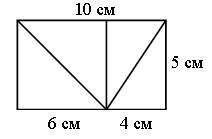
– Сравните площади исходного прямоугольника и треугольника, сторонами которого являются эти диагонали. Проведите необходимые измерения и вычислите площадь данного прямоугольника.  S_□ = 10 · 5 = 50 (кв. см). Вычислите площадь каждого из построенных прямоугольных треугольников.

S_1Δ = 6 · 5 : 2 = 15 (кв. см) S_2Δ = 64 · 5 : 2 = 150 (кв. см)

– Вычислите площадь треугольника, составленного из этих прямоугольных треугольников. S = 15 + 10 = 25 (кв. см).

– Во сколько раз больше площадь прямоугольника, чем площадь треугольника? 50 : 25 = 2 (раза)

Задание 391. Прочитайте высказывания в учебнике. Какие из них можно применить для вычисления площади треугольника, у которого известны длина основания и длина высоты, проведенной к этому основанию?

• Длину основания нужно умножить на половину длины высоты.

• Половину длины основания нужно умножить на длину высоты.

• Длину основания умножить на длину высоты, а полученный результат разделить пополам.

– Вычислите площадь треугольника, у которого длина основания 8 см, а длина соответствующей высоты 5 см.

8 · 5 : 2 = 20 (кв. см).

Задание 392. Проведите необходимые разбиения и измерения для того, чтобы вычислить площадь каждого закрашенного треугольника.

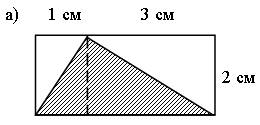
Решение:

I способ.

1) 2 · 1 : 2 = 1 (кв. см).

2) 3 · 2 : 2 = 3 (кв. см).

3) 1 + 3 = 4 (кв. см).

II способ.

4 · 2 : 2 = 4 (кв. см).

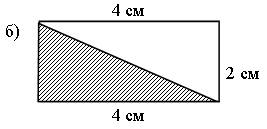
Решение:

4 · 2 : 2 = 4 (кв. см).

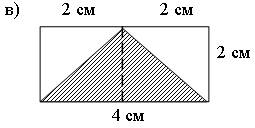
Решение:

4 · 2 : 2 = 4 (кв. см).

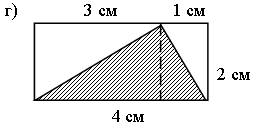
Решение:

I способ.

1) 3 · 2 : 2 = 3 (кв. см).

2) 2 · 1 : 2 = 1 (кв. см).

3) 1 + 3 = 4 (кв. см).

II способ.

4 · 2 : 2 = 4 (кв. см).

III. Итог урока.

– Как вычислить площадь треугольника?

Скачано с www.znanio.ru