Конспект урока по математике на тему"Разбиение многоугольника на треугольники"4класс

Разбиение многоугольника
на треугольники

Цели: учить выполнять чертеж; формировать умение делить отрезками многоугольник на данное количество треугольников; закреплять умение определять количество сторон и количество диагоналей в многоугольнике.

Ход урока

I. Устный счет.

1. Математический диктант.

а) Как называется результат сложения двух чисел?

б) Как называются числа, которые складывают?

в) Чему равна сумма 3456 + 0?

г) Запишите равенство 245 – 181 = 63. С помощью сложения проверьте, правильно ли выполнено вычитание.

д) Найдите значение выражения 981 – х, если х = 0.

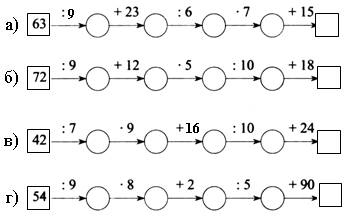
2. Какое число нужно вписать в последнюю клетку цепочки?

3. Как-то раз Пятачок зашёл в гости к Винни-Пуху. Тот в глубокой задумчивости смотрел на лист бумаги, где были нарисованы квадрат и уголок.

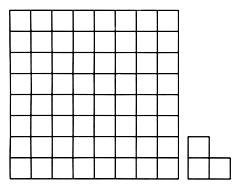
Винни-Пух объяснил, что хочет разрезать квадрат на уголки.

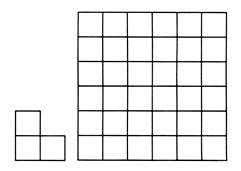
Пятачок внимательно посмотрел на эти фигуры и сказал, что такой квадрат разрезать на такие уголки нельзя. Почему? А вот такой квадрат можно разрезать на уголки. Покажите, как это сделать.

II. Работа по учебнику.

Задание 376. Начертите шестиугольник и проведите все возможные диагонали из одной его вершины.

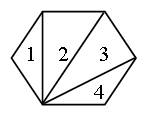
– На какие фигуры эти диагонали разбивают шестиугольник? (На треугольники.) Сколько треугольников получилось? (4 треугольника.)

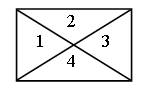
Задание 377. Начертите прямоугольник и разбейте его на 4 треугольника.

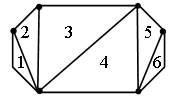
Задание 378. Как называется данный многоугольник? (Восьмиугольник.) Разбейте этот восьмиугольник на 6 треугольников.

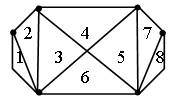
– Разбейте этот же восьмиугольник на 8 треугольников.

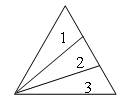
Задание 379. Начертите остроугольный треугольник и разбейте его на 3 треугольника.

Задание 380. Начертите остроугольный треугольник и разбейте его на 2 треугольника так, чтобы один из них был остроугольным, а другой – тупоугольным.

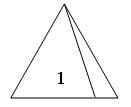
1-й треугольник – остроугольный;

2-й треугольник – тупоугольный.

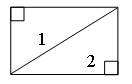
Задание 381. Разбейте прямоугольник на два прямоугольных треугольника. Используя модель прямоугольника, сделанную из бумаги, убедитесь, что полученные прямоугольные треугольники равны.

Задание 382. Начертите остроугольный, прямоугольный и тупоугольный треугольники. Разбейте каждый из них на два прямоугольных треугольника.

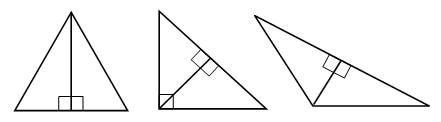
– Как называется отрезок, с помощью которого такое разбиение можно выполнить? (Высота треугольника.)

Задание 383. Как называются данные многоугольники? (Семиугольник, шестиугольник, пятиугольник, четырехугольник, треугольник.)

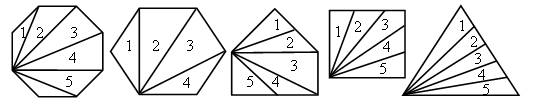
– Каждый многоугольник разбейте на 5 треугольников.

III. Итог урока.

– Как можно разбить многоугольник на треугольники?

Скачано с www.znanio.ru