Конспект урока "Взаимное расположение прямых и плоскостей в пространстве"

Тема 3.1. Начальные понятия стереометрии. Взаимное расположение прямых и плоскостей в пространстве

Занятие № 21 (теоретическое)

Взаимное расположение двух прямых в пространстве.

Параллельность прямой и плоскости.

Параллельность плоскостей.

Цели урока:

ü обучающие: 

·        познакомить с разделом геометрии: стереометрия;

·        изучить аксиомы стереометрии и следствия из них;

·        рассмотреть различные виды расположения прямых в пространстве; расположения прямой и плоскости;

·        ввести определение параллельных и скрещивающихся  прямых в пространстве;

·        определение прямой, параллельной плоскости;

·        изучить теоремы о параллельности прямых и параллельности трёх прямых;

·        сформировать навыки нахождения параллельных и скрещивающихся прямых;

·        прямой, параллельной плоскости на моделях пространственных тел и в окружающих нас объектах;

ü развивающие:

·        развивать у обучающихся пространственное представление, умение переносить пространственные ситуации на плоскость;

·        развивать навыки исследовательской деятельности;

ü воспитывающие:

·        воспитание у студентов аккуратности в построении чертежа,

·        способствовать созданию атмосферы активного творческого труда.

Тип урока: урок изучения нового материала

Время: 1 час 30 мин.                    

Методы проведения: Проблемно-поисковый, деятельностный, метод беседы, методы организации и осуществления учебно-познавательной деятельности, методы контроля и самоконтроля за эффективностью учебно-познавательной деятельности. 

Ход урока

1.          Организационный момент: проверить  готовность группы к уроку, сформулировать тему и цели урока.

2.          Активизация познавательной деятельности учащихся

Преподаватель знакомит с понятием стереометрия:

Геометрия – наука о свойствах геометрических фигур. «Геометрия» - в переводе с греческого – «землемерие» - связано с применением геометрии для измерений на местности. Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма.

3. Новый материал.

Геометрия делится на 2 раздела. В 7-9 классах изучают планиметрию – свойства фигур на плоскости.                    

Сегодня мы начинаем изучать второй раздел геометрии – стереометрию.

Раздел геометрии, изучающий свойства фигур в пространстве, называется стереометрия.

Изучение этого раздела очень важно, поскольку мы живем в пространственном мире и нас окружают пространственные тела. Сложные пространственные тела можно «разбить» на более простые пространственные фигуры. Изучением свойств этих фигур и занимается стереометрия 10-11 классов.

В стереометрии присутствуют три основных понятия: точка, прямая, плоскость. Представление плоскости даёт гладкая поверхность стола, стены. Плоскость следует представлять себе простирающейся во все стороны, не ограниченной. Как можно изобразить плоскость? Наиболее удачный вариант – в виде параллелограмма.

Рассмотрим:

Ø точки А и В, плоскость a, причем точка А лежит в плоскости a, а точка В не лежит в плоскости a.

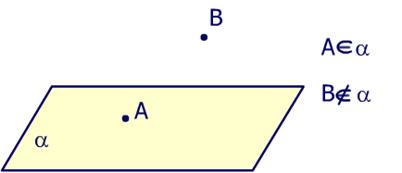
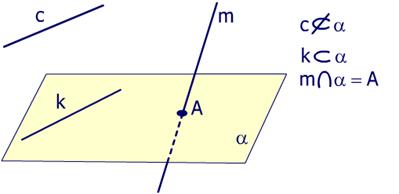
Ø Прямые c, k, m расположены по отношению к плоскости a следующим образом:

·        прямая c не лежит в плоскости a

·        прямая k лежит в плоскости a;

·        прямая m пересекает плоскость a  в точке А.

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах стереометрии: А₁, А₂, А₃

Аксиомы стереометрии

•      А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

•      А2: Если две точки прямой лежат  в плоскости, то все точки прямой лежат в этой плоскости, т.е. прямая лежит в плоскости или плоскость проходит через прямую.

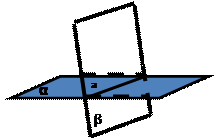•      А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом

Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

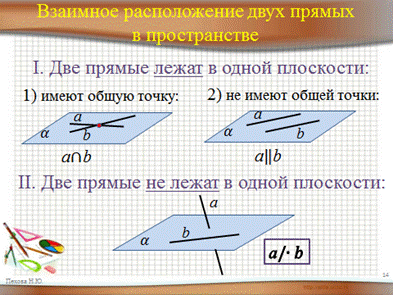
Взаимное расположение прямых в пространстве

Взаимное расположение плоскостей в пространстве

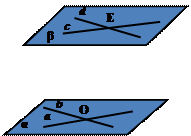
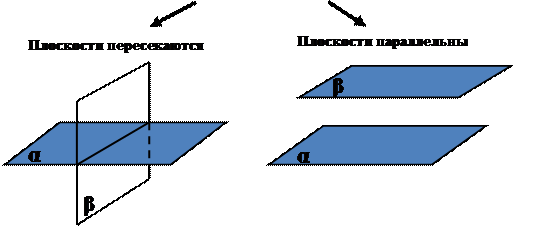
Признак параллельности плоскостей

Теорема. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Если a II c, b II d, то α II β

Свойства параллельных плоскостей

1.     Если две различные плоскости параллельны третьей, то они параллельны между собой.

2.     Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

3.     Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

ВОПРОСЫ:

верно ли утверждение:

·        если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости? (Нет)

·        если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости? (Да)

·        если прямая пересекает две стороны треугольника, то она лежит в плоскости данного треугольника? (Да)

·        если прямая проходит через одну из вершин треугольника, то она лежит в плоскости данного треугольника? (Нет)

·        если две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости, то и две другие вершины тоже лежат в этой плоскости? (Да)

·        если две противоположные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости, то и две другие вершины тоже лежат в этой плоскости? (Нет)

могут ли две плоскости иметь:

·        только одну общую точку? (Нет)

·        только две общие точки? (Нет)

·        только одну общую прямую? (Да)

·        могут ли две пересекающиеся плоскости иметь общую точку, не принадлежащую линии пересечения этих плоскостей? (Нет)

Скачано с www.znanio.ru