
Тема: ПРОИЗВОДНАЯ
№ 1.
Дифференцирование – это …
1. нахождение предела заданной функции
2. нахождение производной заданной функции
3. нахождение функции по ее заданной производной
4. нахождение функции по ее заданному пределу
№ 2.
Выбери обозначение производной II-го порядка:
1.
![]() или
или ![]()
2.
![]() или
или ![]()
3.
![]() или
или ![]()
4.
![]() или
или ![]()
№ 3.
Физический смысл производной I-го порядка заключается в нахождении …
1.
скорости по
правилу ![]()
2.
скорости по
правилу ![]()
3.
ускорения по
правилу ![]()
4.
ускорения по
правилу ![]()
№ 4.
Физический смысл производной II-го порядка заключается в нахождении …
1.
скорости по
правилу ![]()
2.
скорости по
правилу ![]()
3.
ускорения по
правилу ![]()
4.
ускорения по
правилу ![]()
№ 5.
Геометрический смысл производной I-го порядка заключается в нахождении углового коэффициента касательной по правилу …
1.
![]()
2.
![]()
3. ![]()
4. ![]()
№ 6.
Общий вид уравнения касательной к графику функции:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
№ 7.
Точка графика функции, разделяющая промежутки выпуклости и вогнутости называется …
1. точкой максимума
2. точкой минимума
3. точкой перегиба
4. точкой экстремума
№ 8.
Выберите неверное утверждение …
1. В точке перегиба производная II-го порядка может быть равна нулю.
2. В точке перегиба производная II-го порядка может не существовать.
3. В точке перегиба производная II-го порядка всегда равна нулю.
4. В точке перегиба производная II-го порядка либо равна нулю, либо не существует.
№ 9.
Функция вогнута на промежутке, если производная II-го порядка на данном промежутке …
1. положительна.
2. отрицательна.
3. равна нулю.
4. не существует.
№ 10.
Функция выпукла на промежутке, если производная II-го порядка на данном промежутке …
1. положительна.
2. отрицательна.
3. равна нулю.
4. не существует.
№ 11.
Продолжите формулу: ![]() …
…
1.
![]()
2.
![]()
3.
![]()
4.
![]()
№ 12.
Продолжите формулу: ![]() …
…
1.
![]()
2.
![]()
3.
![]()
4.
![]()
№ 13.
Продолжите формулу: ![]() …
…
1.
![]()
2.
![]()
3.
![]()
4.
![]()
№ 14.
Продолжите формулу: ![]() …
…
1.
![]()
2.
![]()
3.
![]()
4.
![]()
№ 15.
Продолжите формулу: ![]() …
…
1.
![]()
2.
![]()
3.
![]()
4.
![]()
№ 16.
Продолжите формулу: 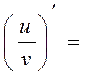 …
…
1.
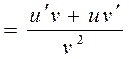
2.
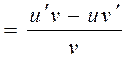
3.
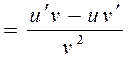
4.
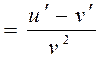
№ 17.
Продолжите формулу: ![]() …
…
1.
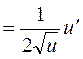
2.
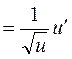
3.
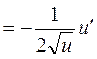
4.
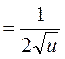
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.