КОНТРОЛЬНАЯ РАБОТА № 3

Контрольная работа № 3

В а р и а н т  1

1. Вычислите:

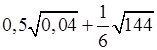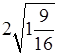а) ;         б)  – 1;         в) .

2. Найдите значение выражения:

а) ;         б) ;         в) ;         г) .

3. Решите уравнение: а) х² = 0,49;         б) х² = 10.

4. Упростите выражение:

а) , где х ≥ 0;         б) 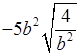, где b < 0.

5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число .

6. При  каких  значениях  переменной  а  имеет  смысл  выражение ?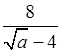

В а р и а н т  2

1. Вычислите:

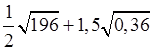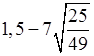а) ;         б) ;         в) .

2. Найдите значение выражения:

а) ;         б) ;         в) ;         г) .

3. Решите уравнение: а) х² = 0,64;         б) х² = 17.

4. Упростите выражение:

а) , где у ≥ 0;         б) 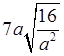, где а < 0.

5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число .

6. При  каких  значениях  переменной  х  имеет  смысл  выражение ?

В а р и а н т  3

1. Вычислите:

а) ;         б) ;         в) .

2. Найдите значение выражения:

а) ;         б) ;         в) ;         г) .

3. Решите уравнение: а) х² = 0,81;         б) х² = 46.

4. Упростите выражение:

а) , где b ≤ 0;         б) , где х > 0.

5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число .

6. При  каких  значениях  переменной  х  имеет  смысл  выражение ?

В а р и а н т  4

1. Вычислите:

а) ;         б) ;         в) .

2. Найдите значение выражения:

а) ;         б) ;         в) ;         г) .

3. Решите уравнение: а) х² = 0,09;         б) х² = 92.

4. Упростите выражение:

а) , где х ≥ 0;         б) , где у < 0.

5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число .

6. При  каких  значениях  переменной  у  имеет  смысл  выражение ?

Решение вариантов контрольной работы

В а р и а н т  1

1. а)  = 0,1 + 2 = 2,1;

    б)  – 1 = 1,5;

    в)  = 2.

2. а)  = 4;

    б)  = 28;

    в)  = 2;

    г)  = 72.

4. а) .

Так как х ≥ 0, то | x | = x. Получим:

.

б) .

Так как b < 0, то | b | = –b. Получим:

.

5. 4,1 <  < 4,2.

6. Чтобы выражение  имело смысл, должны выполняться два условия:

О т в е т: а ≥ 0 и a ≠ 16.

В а р и а н т  2

1. а)  = 7 + 0,9 = 7,9;

    б)  = 1,5 – 5 = –3,5;

    в)  = 6.

2. а)  = 3;

    б)  = 12;

    в)  = 3;

    г)  = 20.

4. а) .

Так как у ≥ 0, то | y | = y. Получим:

.

б) .

Так как а < 0, то | a | = –a. Получим:

 = –28.

5. 6,1 <  < 6,2.

6. Чтобы выражение  имело смысл, должны выполняться два условия:

О т в е т: х ≥ 0 и х ≠ 25.

В а р и а н т  3

1. а)  = 12 – 0,55 = 11,45;

    б)  = –0,5;

    в)  = 5.

2. а)  = 3,6;

    б)  = 60;

    в)  = 5;

    г)  = 54.

4. а) .

Так как b ≤ 0, то | b | = –b. Получим:

.

б) .

Так как х > 0, то | x | = x. Получим:

 = 14x.

5. 5,2 <  < 5,3.

6. Чтобы выражение  имело смысл, должны выполняться два условия:

О т в е т: х ≥ 0 и х ≠ 4.

В а р и а н т  4

1. а)  = 2 + 0,3 = 2,3;

    б)  = 2,1 + 0,9 = 3;

    в)  = 0,8.

2. а)  = 3;

    б)  = 42;

    в)  = 4;

    г)  = 56.

4. а) .

Так как х ≥ 0, то . Получим:

.

б) .

Так как у < 0, то . Получим:

.

5. 7,4 <  < 7,5.

6. Чтобы выражение  имело смысл, должны выполняться два условия:

О т в е т: у ≥ 0.