КОНТРОЛЬНАЯ РАБОТА № 5 «СУММА И РАЗНОСТЬ МНОГОЧЛЕНОВ. ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ»

Контрольная работа № 5 «Сумма и разность многочленов. произведение многочленов»

 

Вариант 1

1. Выполните действия.

а) (3a – 4ax + 2) – (11a – 14ax);

б) 3y² (y³ + 1).

2. Вынесите общий множитель за скобки.

а) 10ab – 15b²;                        б) 18а³ + 6а².

3. Решите уравнение  9х – 6 (х – 1) = 5 (х + 2).

4. Пассажирский поезд за 4 ч прошёл такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.

5. Решите уравнение  .

6. Упростите выражение  2a (a + b – c) – 2b (a – b – c) + 2c (a – b + c).

Вариант 2

1. Выполните действия.

а) (2a² – 3a + 1) – (7a² – 5a);

б) 3х (4х² – х).

2. Вынесите общий множитель за скобки.

а) 2ху – 3ху²;                            б) 8b⁴ + 2b³.

3. Решите уравнение  7 – 4 (3х – 1) = 5 (1–2х).

4. В трех шестых классах 91 ученик. В 6 «А» на 2 ученика меньше, чем в 6 «Б», а в 6 «В» на 3 ученика больше, чем в 6 «Б». Сколько учащихся в каждом классе?

5. Решите уравнение  .

6. Упростите выражение  3x (x + y + c) – 3y (x – y – c) – 3c (x + y – c).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант 3

1. Выполните действия.

а) (12ab – 5a) – (ab + 6a);

б) 5х (3х² – 2х – 4).

2. Вынесите общий множитель за скобки.

а) 3х² + 9ху;                              б) 10х⁵ – 5х.

3. Решите уравнение  4 (х + 1) = 15х – 7 (2х + 5).

4. Ученик за 8 ч работы сделал столько же деталей, сколько мастер за 5 ч. Сколько деталей в час изготовил ученик, если известно, что мастер изготовлял в час на 6 деталей больше, чем ученик?

5. Решите уравнение  .

6. Упростите выражение  4х (a + х + y) + 4a (a – х – y) – 4y (х – a – y).

Вариант 4

1. Выполните действия.

а) (4y³ + 15y) – (17y – y³);

б) 2a (3a – b + 4).

2. Вынесите общий множитель за скобки.

а) 2ab – ab²;                             б) 2х² + 4х⁶.

3. Решите уравнение  5 (х – 3) = 14 – 2 (7 – 2х).

4. В трёх корзинах 56 кг яблок. Во второй корзине на 12 кг яблок больше, чем в первой, а в третьей – в 2 раза больше, чем в первой. Сколько килограммов яблок в каждой корзине?

5. Решите уравнение  .

6. Упростите выражение  6a (a – х + c) + 6х (a + х – c) – 6c (a – х – c).

Решение заданий контрольной работы

Вариант 1

1. а) (3a – 4ax + 2) – (11a – 14ax) = 3a – 4ax + 2 – 11a + 14ax =

= 10ax – 8a + 2;

    б) 3y² (y³ + 1) = 3y⁵ + 3y².

2. а) 10ab – 15b² = 5b (2a – 3b);

    б) 18а³ + 6а² = 6а² (3а + 1).

3. 9х – 6 (х – 1) = 5 (х + 2);

    9х – 6х + 6 = 5х + 10;

    3х – 5х = 10 – 6;

    –2х = 4;

    х = –2.

Ответ: –2.

4. Составим таблицу:

Известно,  что  поезда  прошли  одинаковое  расстояние.  Получим уравнение:

4х = 6 (х – 20);

4х = 6х – 120;

–2х = –120;

х = 60.

Ответ: 60 км/ч.

5. .

Умножим обе части уравнения на 18:

;

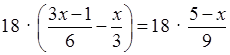3 (3х – 1) – 6х = 2 (5 – х);

9х – 3 – 6х = 10 – 2х;

3х + 2х = 10 + 3;

5х = 13;

х = ;

х = 2,6.

Ответ: 2,6.

6.
–2ac – 2ab + 2b² + 2bc + 2ac – 2bc + 2c² = 2a² + 2b² + 2c².

Вариант 2

1. а) (2a² – 3a + 1) – (7a² – 5a) = 2a² – 3a + 1 – 7a² + 5a = –5a² + 2a + 1;

    б) 3х (4х² – х) = 12х³ – 3х².

2. а) 2ху – 3ху² = ху (2 – 3у);

    б) 8b⁴ + 2b³ = 2b³ (4b + 1).

3. 7 – 4 (3х – 1) = 5 (1–2х);

    7 – 12х + 4 = 5 – 10х;

    – 12х + 10х = 5 – 11;

    –2х = –6;

    х = 3.

Ответ: 3.

4. Пусть в 6 «Б» классе всего х учеников. Тогда в 6 «А» (х – 2) ученика, а в 6 «В» (х + 3) ученика.

По  условию  всего  в  трех  классах  91  ученик.  Составим  и  решим уравнение.

х + (х – 2) + (х + 3) = 91;

х + х – 2 + х + 3 = 91;

3х = 90;

х = 30.

Значит, в 6 «Б» классе 30 учеников. Тогда в 6 «А» 28 учеников, а в 6 «В» 33 ученика.

Ответ: 28, 30 и 33 ученика.

5. .

Умножим обе части уравнения на 20.

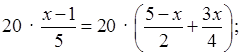
4 (х – 1) = 10 (5 – х) + 15х;

4х – 4 = 50 – 10х + 15х;

4х – 5х = 50 + 4;

–х = 54;

х = –54.

Ответ: –54.

6.
+ 3хc – 3хy + 3y² + 3yc – 3хc – 3yc + 3c² = 3х² + 3y² + 3c².

Вариант 3

1. а) (12ab – 5a) – (ab + 6a) = 12ab – 5a – ab – 6a = 11ab – 11a;

    б) 5х (3х² – 2х – 4) = 15х³ – 10х² – 20х.

2. а) 3х² + 9ху = 3х (х + 3у);

    б) 10х⁵ – 5х = 5х (2х⁴ – 1).

3. 4 (х + 1) = 15х – 7 (2х + 5);

    4х + 4 = 15х – 14х – 35;

    4х – х = –35 – 4;

    3х = –39;

    х = –13.

Ответ: –13.

4. Составим таблицу:

По условию мастер и ученик изготовили одинаковое количество деталей. Получим уравнение:

8х = 5 (х + 6);

8х = 5х + 30;

3х = 30;

х = 10.

Ответ: 10 деталей.

5. .

Умножим обе части уравнения на 12:

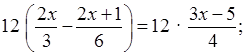
8х – 2 (2х + 1) = 3 (3х – 5);

8х – 4х – 2 = 9х – 15;

4х – 9х = – 15 + 2;

–5х = –13;

х = .

х = 2,6

Ответ: 2,6.

6.

+ 4хy + 4a² – 4aх – 4ay – 4хy + 4ay + 4y² = 4х² + 4a² + 4y².

Вариант 4

1. а) (4y³ + 15y) – (17y – y³) = 4y³ + 15y – 17y + y³ = 5y³ – 2y;

    б) 2a (3a – b + 4) = 6a² – 2ab + 8a.

2. а) 2ab – ab² = ab (2 – b);

    б) 2х² + 4х⁶ = 2х² (1 + 2х⁴).

3. 5 (х – 3) = 14 – 2 (7 – 2х);

    5х – 15 = 14 – 14 + 4х;

    5х – 4х = 15;

    х = 15.

Ответ: 15.

4. Пусть в первой корзине х кг яблок. Тогда во второй корзине (х + 12) кг яблок, а в третьей 2х кг яблок.

По условию всего в трёх корзинах 56 кг яблок. Составим и решим уравнение:

х + х + 12 + 2х = 56;

4х = 44;

х = 11.

Значит, в первой корзине 11 кг яблок. Тогда во второй корзине 23 кг яблок, а в третьей – 22 кг яблок.

Ответ: 11, 23 и 22 кг яблок.

5. .

Умножим обе части уравнения на 12:

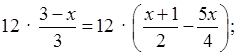
4 (3 – х) = 6 (х + 1) – 15х;

12 – 4х = 6х + 6 – 15х;

–4х + 9х = 6 – 12;

5х = –6;

х = ;

х = –1,2.

Ответ: –1,2.

6.

+ 6ac + 6ax + 6x² – 6cx – 6ac + 6cx + 6c² = 6a² + 6x² + 6c².