КОНТРОЛЬНАЯ РАБОТА № 9

Контрольная работа № 9

Вариант 1

1. Решите систему уравнений: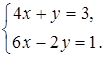

2. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р. и 3000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19000 р.?

3. Решите систему уравнений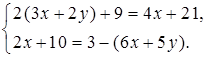

4. Прямая y = kx + b проходит через точки А (3; 8) и В (–4; 1). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько: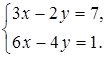

Вариант 2

1. Решите систему уравнений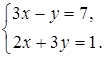

2. Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе и с какой скоростью по лесной дороге?

3. Решите систему уравнений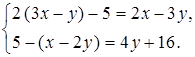

4. Прямая y = kx + b проходит через точки А (5; 0) и В (–2; 21). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько: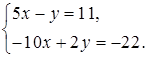

Вариант 3

1. Решите систему уравнений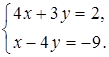

2. На турбазе имеются палатки и домики, вместе их 25. В каждом домике живут 4 человека, а в палатке – 2 человека. Сколько на турбазе палаток и сколько домиков, если турбаза рассчитана на 70 человек?

3. Решите систему уравнений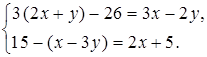

4. Прямая y = kx + b проходит через точки А (10; –9) и В (–6; 7). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько: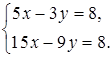

Вариант 4

1. Решите систему уравнений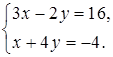

2. За 15 акций компании «Трансгаз» и 10 акций компании «Суперсталь» заплатили 35000 р. Сколько стоит одна акция каждой компании, если акция «Трансгаза» на 1000 р. дешевле акции «Суперстали»?

3. Решите систему уравнений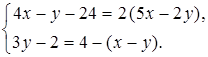

4. Прямая y = kx + b проходит через точки А (–2; 11) и В (12; 4). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько: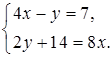

Вариант 1

1. Решите систему уравнений:

2. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р. и 3000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19000 р.?

3. Решите систему уравнений

4. Прямая y = kx + b проходит через точки А (3; 8) и В (–4; 1). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько:

Вариант 2

1. Решите систему уравнений

2. За 15 акций компании «Трансгаз» и 10 акций компании «Суперсталь» заплатили 35000 р. Сколько стоит одна акция каждой компании, если акция «Трансгаза» на 1000 р. дешевле акции «Суперстали»?

3. Решите систему уравнений

4. Прямая y = kx + b проходит через точки А (–2; 11) и В (12; 4). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько:

Вариант 1

1. Решите систему уравнений:

2. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р. и 3000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19000 р.?

3. Решите систему уравнений

4. Прямая y = kx + b проходит через точки А (3; 8) и В (–4; 1). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько:

Вариант 2

1. Решите систему уравнений

2. За 15 акций компании «Трансгаз» и 10 акций компании «Суперсталь» заплатили 35000 р. Сколько стоит одна акция каждой компании, если акция «Трансгаза» на 1000 р. дешевле акции «Суперстали»?

3. Решите систему уравнений

4. Прямая y = kx + b проходит через точки А (–2; 11) и В (12; 4). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько:

Вариант 1

1. Решите систему уравнений:

2. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р. и 3000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19000 р.?

3. Решите систему уравнений

4. Прямая y = kx + b проходит через точки А (3; 8) и В (–4; 1). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько:

Вариант 2

1. Решите систему уравнений

2. За 15 акций компании «Трансгаз» и 10 акций компании «Суперсталь» заплатили 35000 р. Сколько стоит одна акция каждой компании, если акция «Трансгаза» на 1000 р. дешевле акции «Суперстали»?

3. Решите систему уравнений

4. Прямая y = kx + b проходит через точки А (–2; 11) и В (12; 4). Напишите уравнение этой прямой.

5. Выясните, имеет ли решение система и сколько:

Решение заданий контрольной работы

Вариант 1

1.

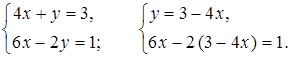
6х – 2(3 – 4х) = 1;

6х – 6 + 8х = 1;

14х = 7;

х = 0,5;

у = 3 – 4 · 0,5;

у = 1.

Ответ: (0,5; 1).

2. Пусть  г-н  Разин  купил  х  облигаций  по  2000  р.  и  у  облигаций по 3000 р.

По  условию  всего  он  купил  8  облигаций,  то  есть  получим  уравнение: х + у = 8.

За облигации номинала 2000 р. предприниматель заплатил 2000 х р., а за облигации номинала 3000 р. заплатил 3000у р. Всего за облигации было заплачено 19000 р., то есть получим уравнение: 2000х + 3000у = 19000.

Составим и решим систему уравнений:

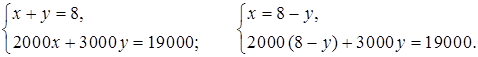
2000 (8 – у) + 3000у = 19000;

16000 – 2000у + 3000у = 19000;

1000у = 3000;

у = 3;

х = 8 – 3;

х = 5.

Ответ: 5 облигаций по 2000 р. и 3 облигации по 3000 р.

3.

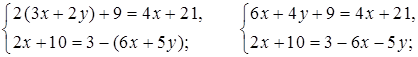
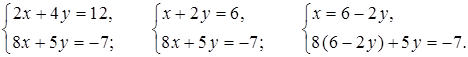
8 (6 – 2у) + 5у = –7;

48 – 16у + 5у = –7;

–11у = –55;

у = 5;

х = 6 – 2 · 5;

х = –4.

Ответ: (–4; 5).

4. Подставляя координаты точек А и В в уравнение y = kx + b, получим систему уравнений:

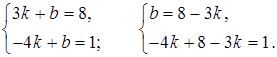
–4k + 8 – 3k = 1;

–7k = –7;

k = 1;

b = 8 – 3;

b = 5;

у = х + 5.

Ответ: у = х + 5.

5. Выразим в каждом уравнении системы у через х и сравним коэффициенты k и b:

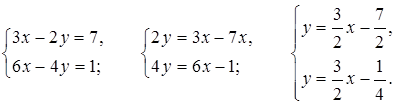
Так как коэффициенты k равны, а b не равны, то прямые параллельны. Значит, система не имеет решений.

Ответ: не имеет.

Вариант 2

1.

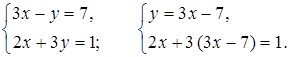
2х + 3 (3х – 7) = 1;

2х + 9х – 21 = 1;

11х = 22;

х = 2;

у = 3 · 2 – 7;

у = –1.

Ответ: (2; –1).

2. Пусть по лесной дороге велосипедист ехал со скоростью х км/ч, а по шоссейной – со скоростью у км/ч.

На шоссе его скорость была на 4 км/ч больше, поэтому получим уравнение: у – х = 4.

За 2 ч по лесной дороге и 1 ч по шоссе велосипедист проехал (2х + у) км, по условию всего он проехал 40 км. Получим уравнение: 2х + у = 40.

Составим и решим систему уравнений:

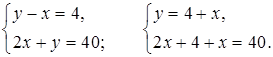
3х + 4 = 40;

3х = 36;

х = 12;

у = 4 + 12;

у = 16.

Ответ: 16 км/ч и 12 км/ч.

3.

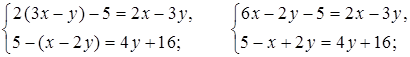
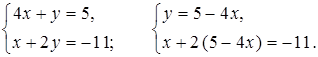
2 (5 – 4х) + х = –11;

10 – 8х + х = –11;

–7х = –21;

х = 3;

у = 5 – 4 · 3;

у = –7.

Ответ: (3; –7).

4. Подставляя координаты точек А и В в уравнение y = kx + b, получим систему уравнений:

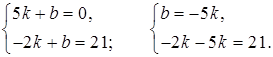
–7k = 21;

k = –3;

b = –5 · (–3);

b = 15.

Ответ: у = –3х + 15.

5. Выразим в каждом уравнении системы у через х и сравним коэффициенты k и b:

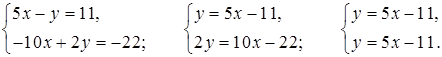
Получили два одинаковых уравнения, значит, система имеет бесконечное множество решений.

Ответ: имеет бесконечное множество решений.

Вариант 3

1.

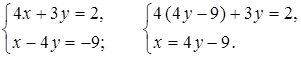
4 (4у – 9) + 3у = 2;

16у – 36 + 3у = 2;

19у = 38;

у = 2;

х = 4 · 2 – 9;

х = –1.

Ответ: (–1; 2).

2. Пусть на турбазе х палаток и у домиков.

По условию их всего 25, то есть получаем уравнение: х + у = 25.

В домиках живут 4у человек, а в палатках 2х человек. Всего на турбазе находится 70 человек. Получим уравнение: 2х + 4у = 70.

Составим и решим систему уравнений:

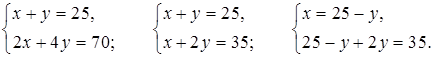
25 + у = 35;

у = 10;

х = 25 – 10;

х = 15.

Ответ: 15 палаток и 10 домиков.

3.

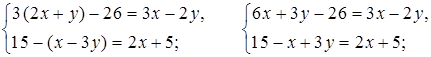
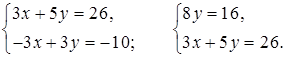
8у = 16;

у = 2;

3х + 10 = 26;

3х = 16;

х = 5.

Ответ: .

4. Подставляя координаты точек А и В в уравнение y = kx + b, получим систему уравнений:

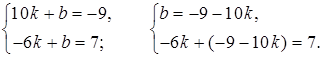
–6k – 9 – 10k = 7;

–16k = 16;

k = –1;

b = –9 – 10 · (–1);

b = 1.

Ответ: у = –х + 1.

5. Выразим в каждом уравнении системы у через х и сравним коэффициенты k и b:

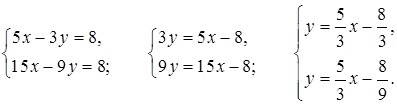
Так как коэффициенты k равны, а b не равны, то прямые параллельны. Значит, система не имеет решений.

Ответ: не имеет.

Вариант 4

1.

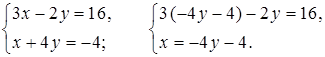
3 (–4у – 4) – 2у = 16;

–12у – 12 – 2у = 16;

–14у = 28;

у = –2;

х = –4 · (–2) – 4;

х = 4.

Ответ: (4; –2).

2. Пусть одна акция «Трансгаза» стоит х р., а одна акция «Суперстали» стоит у р.

Известно, что акция «Трансгаза» на 1000 р. дешевле, поэтому получим уравнение: у – х = 1000.

За  15  акций  «Трансгаза»  было  заплачено  15х р., а за 10 акций «Суперстали» – 10у р. Известно, что всего заплатили 35000. Получим уравнение: 15х + 10у = 35000.

Составим и решим систему уравнений:

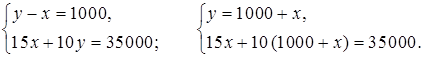
15х + 10 (1000 + х) = 35000;

15х + 10000 + 10х = 35000;

25х = 25000;

х = 1000;

у = 1000 + 1000;

у = 2000.

Ответ: 1000 р. и 2000 р.

3.

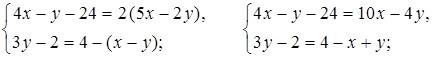
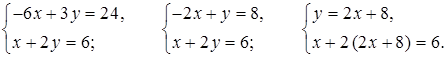
х + 2 (2х + 8) = 6;

х + 4х + 16 = 6;

5х = –10;

х = –2;

у = 2 · (–2) + 8;

у = 4.

Ответ: (–2; 4).

4. Подставляя координаты точек А и В в уравнение y = kx + b, получим систему уравнений:

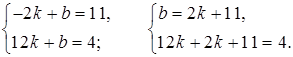
14k + 11 = 4;

14k = –7;

k = –0,5;

b = 2 · (–0,5) + 11;

b = 10.

Ответ: у = –0,5х + 10.

5. Выразим в каждом уравнении системы у через х и сравним коэффициенты k и b:

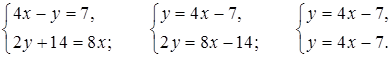
Получили два одинаковых уравнения, значит, система имеет бесконечное множество решений.

Ответ: имеет бесконечное множество решений.