Контрольная работа "Исследование функций с помощью производной", 11 класс

А-11        Контрольная работа «Исследование функций с помощью производной»

Вариант 1

1.Материальная точка движется прямолинейно по закону x(t) =  t³ – 3t² – 5t + 3, (где x — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?         

2. Материальная точка движется прямолинейно по закону х(t)  = - t⁴ + 6t³ + 5t + 23, (где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения). Найдите ее ускорение в (м/с²) в момент времени t = 3 c.

3.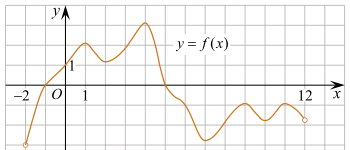На ри­сун­ке изоб­ра­жен гра­фик функ­ции y  =  f(x), опре­де­лен­ной на ин­тер­ва­ле (−2; 12). Най­ди­те сумму точек экс­тре­му­ма функ­ции f(x).

4.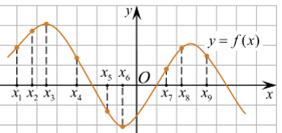На ри­сун­ке изоб­ражён гра­фик диф­фе­рен­ци­ру­е­мой функ­ции y  =  f(x). На оси абс­цисс от­ме­че­ны де­вять точек: x₁, x₂, x₃, ..., x₉. Среди этих точек най­ди­те все точки, в ко­то­рых про­из­вод­ная функ­ции f(x) от­ри­ца­тель­на. В от­ве­те ука­жи­те ко­ли­че­ство най­ден­ных точек

5.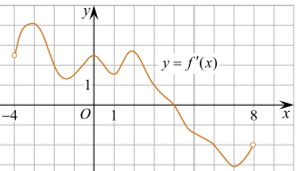На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−4; 8). Най­ди­те точку экс­тре­му­ма функ­ции f(x) на от­рез­ке [−2; 6].

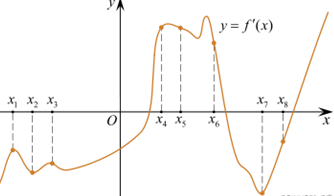
6. На ри­сун­ке изоб­ражён гра­фик   — про­из­вод­ной функ­ции f(x). На оси абс­цисс от­ме­че­ны во­семь точек: x₁, x₂, x₃, ..., x₈. Сколь­ко из этих точек лежит на про­ме­жут­ках воз­рас­та­ния функ­ции f(x)?

7. Най­ди­те точку мак­си­му­ма функ­ции  y = ln(x + 5) – 2x + 9.

8. Най­ди­те наи­мень­шее зна­че­ние функ­ции y  =  15 + 12x + x³ на от­рез­ке [−2; 2].