Контрольная работа по алгебре для 8 класса по теме "Квадратные корни"

Контрольная работа по теме «Квадратные корни»

Вариант 1

1. Найдите значение арифметического квадратного корня:   а) ; б) .

2. Вынести множитель за знак корня:   

3. Вычислите: а) ; б) ; в) , 

4. Упростить выражение: а) а) 

5. Исключите иррациональность из знаменателя:   а) ; б) .

6. Упростите выражение: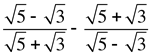 

______________________________________________________________

Контрольная работа  по теме «Квадратные корни»

Вариант 2

1. Найдите значение арифметического квадратного корня:    а) ; б) .

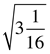2. Вынести множитель за знак корня:   

3. Вычислите: а) ; б) ; в) .

4. Упростить выражение: а) 

5. Исключите иррациональность из знаменателя:     а) ; б) .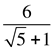

6. Упростите выражение: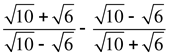 

Вариант 1

1. Дана ариф­ме­ти­че­ская про­грес­сия   Най­ди­те  .

2. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна 2,5, a₁ = 8,7. Най­ди­те a₉.

3. Дана арифметическая прогрессия   Найдите сумму первых десяти её членов.

4. В гео­мет­ри­че­ской про­грес­сии  известно, что . Найти пятый член этой прогрессии.

5. Дана гео­мет­ри­че­ская про­грес­сия (b_n), зна­ме­на­тель ко­то­рой равен 2, а . Най­ди­те сумму пер­вых шести её членов.

6. Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b₃ = , b₆ = -196. Най­ди­те зна­ме­на­тель прогрессии.

Вариант 2

1. В ариф­ме­ти­че­ской про­грес­сии    известно, что  . Най­ди­те четвёртый член этой прогрессии.

2. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна −8,5, a₁ = −6,8. Най­ди­те a₁₁.

3. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна −2,5, a₁ = −9,1. Най­ди­те сумму пер­вых 15 её членов.

4. Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: 17, 68, 272, ... Най­ди­те её четвёртый член.

5. Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: −1024; −256; −64; … Най­ди­те сумму пер­вых 5 её членов.

6. Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b₅ = −14, b₈ = 112. Най­ди­те зна­ме­на­тель прогрессии.

Вариант 1

1. Дана ариф­ме­ти­че­ская про­грес­сия   Най­ди­те  .

2. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна 2,5, a₁ = 8,7. Най­ди­те a₉.

3. Дана арифметическая прогрессия   Найдите сумму первых десяти её членов.

4. В гео­мет­ри­че­ской про­грес­сии  известно, что . Найти пятый член этой прогрессии.

5. Дана гео­мет­ри­че­ская про­грес­сия (b_n), зна­ме­на­тель ко­то­рой равен 2, а . Най­ди­те сумму пер­вых шести её членов.

6. Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b₃ = , b₆ = -196. Най­ди­те зна­ме­на­тель прогрессии.

Вариант 1

1. Дана ариф­ме­ти­че­ская про­грес­сия   Най­ди­те  .

2. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна 2,5, a₁ = 8,7. Най­ди­те a₉.

3. Дана арифметическая прогрессия   Найдите сумму первых десяти её членов.

4. В гео­мет­ри­че­ской про­грес­сии  известно, что . Найти пятый член этой прогрессии.

5. Дана гео­мет­ри­че­ская про­грес­сия (b_n), зна­ме­на­тель ко­то­рой равен 2, а . Най­ди­те сумму пер­вых шести её членов.

6. Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b₃ = , b₆ = -196. Най­ди­те зна­ме­на­тель прогрессии.

Вариант 2

1. В ариф­ме­ти­че­ской про­грес­сии    известно, что  . Най­ди­те четвёртый член этой прогрессии.

2. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна −8,5, a₁ = −6,8. Най­ди­те a₁₁.

3. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна −2,5, a₁ = −9,1. Най­ди­те сумму пер­вых 15 её членов.

4. Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: 17, 68, 272, ... Най­ди­те её четвёртый член.

5. Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: −1024; −256; −64; … Най­ди­те сумму пер­вых 5 её членов.

6. Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b₅ = −14, b₈ = 112. Най­ди­те зна­ме­на­тель прогрессии.

Вариант 2

1. В ариф­ме­ти­че­ской про­грес­сии    известно, что  . Най­ди­те четвёртый член этой прогрессии.

2. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна −8,5, a₁ = −6,8. Най­ди­те a₁₁.

3. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна −2,5, a₁ = −9,1. Най­ди­те сумму пер­вых 15 её членов.

4. Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: 17, 68, 272, ... Най­ди­те её четвёртый член.

5. Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: −1024; −256; −64; … Най­ди­те сумму пер­вых 5 её членов.

6. Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b₅ = −14, b₈ = 112. Най­ди­те зна­ме­на­тель прогрессии.