Контрольная работа по геометрии "Объёмы многогранников"

Г-11           Контрольная работа  «Объёмы многогранников»

Вариант 1                       

1.    Диа­го­наль куба равна.  Най­ди­те его объем.

2.        Аквариум имеет форму прямоугольного параллелепипеда с размерами 60 см × 20 см × 50 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.    

3.        Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 16. У второй пирамиды высота в 2 раза больше, а сторона основания в 1,5 раза больше, чем у первой. Найди объём второй пирамиды. 

4.        В сосуд, имеющий форму прав.треугольной призмы,налили2300см³ воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки25см до отметки27см. Найди объем детали. Ответ в см³.

5. 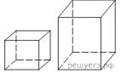        Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй коробки больше объёма первой?

6.        В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC ме­ди­а­ны ос­но­ва­ния ABC пе­ре­се­ка­ют­ся в точке О. Пло­щадь тре­уголь­ни­ка ABC равна 9, a объем пи­ра­ми­ды равен 6. Най­ди­те длину от­рез­ка OS.

7.        В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ заданы длины ребер AD  =  12, AB  =  5, AA₁  =  8.

 а)  Докажите, что плоскость  ВDA₁ делит объем параллелепипеда в отношении 1:5.

 б)  Найдите объем пирамиды MB₁C₁D, если M  — точка на ребре AA₁, причем AM  =  5.

8.  В правильной треугольной призме ABCA₁B₁C₁ все рёбра равны 6. На рёбрах AA₁ и CC₁ отмечены точки   M и N соответственно, причём AM  =  2, CN  =  1.

      а)  Докажите, что плоскость MNB₁ разбивает призму на два многогранника, объёмы которых равны.

      б)  Найдите объём тетраэдра MNBB₁.

Контрольная работа по геометрии 11 класс по теме

«Объёмы многогранников», составлена в соответствии с требованиями ФГОС СОО.

Контрольная работа представлена в двух вариантах и содержит 8заданий:

                      Часть 1  - 6 заданий базового уровня,

                      Часть 2  - 2 задания с подробным решением.

Критерии оценивания работы

За любое верно выполненное задание Части 1 обучающийся получает 1 балл.

За верно каждое выполненное задание Части 2 обучающийся получает 2 балла. Максимальное количество баллов – 10.

Критерии выставления оценок

Ответы к контрольной работе по геометрии 11 класс по теме «Объёмы многогранников»

Ответы: 1) 8           2) 60            3) 72           4) 184           5) 6

6) Решение. Отрезок OS является высотой треугольной пирамиды SABC, ее объем выражается

формулойТаким образом,

7) Решение. 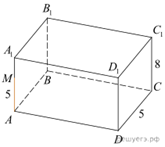а)  Одна из полученных частей это треугольная пирамида    Её высота равна высоте параллелепипеда, а площадь её основания равна половине площади основания параллелепипеда. Тогда в силу формулы объема пирамиды, получаем, что объем пирамиды относится к объему параллелепипеда как 1:6. А это эквивалентно тому, что требуется доказать.

б)  Заметим, что   Площадь прямоугольного треугольника, лежащего в основании, равна половине произведения катетов:

Основание пирамиды лежит в плоскости поэтому высотой пирамиды будет являться перпендикуляр, опущенный из точки M на эту плоскость. Опустим перпендикуляр ME на прямую Поскольку и в силу того, что отрезок ME является высотой пирамиды:

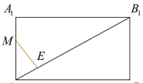Треугольник AME подобен треугольнику значит,

                                                                  Ответ: 50.

8) В правильной треугольной призме ABCA₁B₁C₁ все рёбра равны 6. На рёбрах AA₁ и CC₁ отмечены точки M и N соответственно, причём AM  =  2, CN  =  1.

а)  Докажите, что плоскость MNB₁ разбивает призму на два многогранника, объёмы которых равны.

б)  Найдите объём тетраэдра MNBB₁.

Решение. 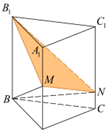Площадь основания призмы равна 9, а объём призмы равен 54.

В четырёхугольной пирамиде B₁A₁C₁NM высота совпадает с высотой основания призмы A₁B₁C₁, опущенной на сторону A₁C₁, и равна 3. Основание A₁C₁NM пирамиды B₁A₁C₁NM является трапецией, площадь которой равна 27. Значит, объём пирамиды B₁A₁C₁NM равен 27, то есть составляет половину объёма призмы. Поэтому объёмы многогранников B₁A₁C₁NM и ABCMB₁N равны.

б)  В четырёхугольной пирамиде BACNM высота совпадает с высотой основания призмы ABC, опущенной на сторону AC, и равна 3. Основание пирамиды BACNM является трапецией, площадь которой равна 9. Объём пирамиды BACNM равен 9

Многогранник ABCMB₁Nсостоит из двух частей: BACNM и MNBB₁.Т.е, объём тетраэдра MNBB₁ равен 18