Контрольная работа по теме "Пирамида".

Контрольная работа по теме «Пирамида».

Вариант 1.

1.

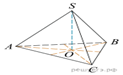
В правильной треугольной пирамиде SABC с вершиной S биссектрисы треугольника ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 6. Найдите длину отрезка OS.

2.

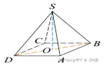В правильной четырехугольной пирамиде SABCD точка O − центр основания, S − вершина, Найдите:  а) боковое ребро  ;  б) объем пирамиды.

Ответ: 17.

3.

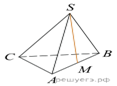
В правильной треугольной пирамиде SABC точка M − середина ребра AB, S − вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.

4.

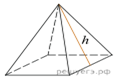
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

5.

Во сколько раз увеличится а) объем правильного тетраэдра, если все его ребра увеличить в три раза?  б) поверхность правильного тетраэдра, если все его ребра увеличить в три раза?

6. 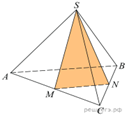От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

7.

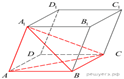
Объем параллелепипеда равен 90. Найдите объем треугольной пирамиды

8.

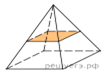
В правильной четырёхугольной пирамиде объем равен 128. Найдите объем малой пирамиды, полученной сечением  плоскостью, проходящей через середины боковых рёбер.

9.  

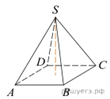В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

 10.

Ребра тетраэдра равны 6. Найдите а) площадь сечения, проходящего через середины четырех его ребер.

 11.

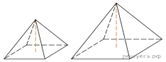Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 18. У второй пирамиды высота в 2 раза больше, а сторона основания в 1,5 раза меньще, чем у первой. Найдите объём второй пирамиды.

12. Плоскость, проходящая через точки A, B и C (см. рис.), разбивает тетраэдр на два многогранника. Сколько  граней  у получившегося многогранника с бо́льшим числом вершин?

13. 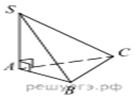В основании пирамиды SABC лежит правильный треугольник ABC со стороной 10, а боковое ребро SA перпендикулярно основанию и равно Найдите объём пирамиды SABC.

14.

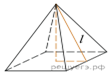
Найдите площадь  поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.

Вариант 2.

1.

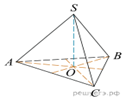
В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке Площадь треугольника ABC равна 9; объем пирамиды равен 6. Найдите а) длину отрезка

 2.

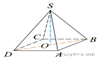
В правильной четырехугольной пирамиде SABCD точка O − центр основания, S − вершина, Найдите а) длину отрезка     б) объем пирамиды.

3.

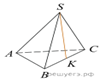
В правильной треугольной пирамиде SABC точка K − середина ребра BC, S − вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.

 4.

Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

5.

Во сколько раз увеличится а) площадь поверхности октаэдра, если все его ребра увеличить в 4 раза?  б)  объем октаэдра, если все его ребра увеличить в 4 раза?  

6.

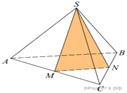От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем оставшейся части пирамиды.

7.

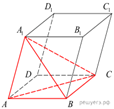
Объем параллелепипеда равен 24. Найдите объем треугольной пирамиды

8.

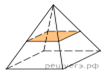
В правильной четырёхугольной пирамиде объем равен 256. Найдите объем малой  пирамиды, полученной сечением  плоскостью, проходящей через середины боковых рёбер.

9.

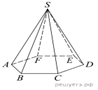Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.    

10.

Ребра тетраэдра равны 18. Найдите а) площадь сечения, проходящего через середины четырех его ребер.

11.

Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 20. У второй пирамиды высота в 2,5 раза  меньше, а сторона основания в 1,5 раза больше, чем у первой. Найдите объём второй пирамиды.

12.

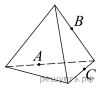Плоскость, проходящая через точки A, B и C (см. рис.), разбивает тетраэдр на два многогранника. Сколько  рёбер у получившегося многогранника с бо́льшим числом вершин?

13.

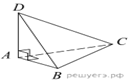В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB = 6, AC = 18 и AD = 8.

14.

Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 12 и высота равна 8.