Поделиться
kontrolnye_raboty 8 КЛАСС.docx
Контрольная работа №1 по теме «Простейшие функции»
I вариант
1. Изобразите на координатной оси числовой промежуток:
[-3;2]; (-5; - 2]; (-2; 5), (2; 8) (-∞; 6] (-6; 1] (2; +∞)
2. Дана функция у = 1/х.
а)Принадлежат ли точки А(- 0,1; 10), В(-0,2; - 5), С(2; 0,5) графику этой функции?
б) Какому числовому промежутку принадлежат значения у, если х Î [1; 2]?
3. Постройте график функции у = х2.
Возрастает или убывает эта функция на промежутке: а) (- ∞; 0]; б) [0; + ∞)?
4.
.
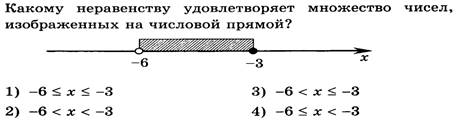
5. 4 Какие целые числа принадлежат
промежутку
-5<Х<6
5 Укажите наименьшее число
-8≤Х<3
5. Какие целые числа принадлежат промежутку -5<Х<6?
Укажите наименьшее число из промежутка -8≤Х<3.
II вариант
1. Изобразите на координатной оси числовой промежуток:
[- 2; 3]; (-6; - 3]; (-5; 3) [-8;9); 3) [-2; 2]; 5) (11;+ ∞);
2. Дана функция у = х2.
а) Принадлежат ли точки А(-10; -100), B(8; 64), С(- 6; 36) графику этой функции?
б) Какому числовому промежутку принадлежат значения у, если х Î [1; 5]?
3. Постройте график функции y
= 
Возрастает
или убывает эта функция на промежутке:
а) (- ∞; 0); б) (0; + ∞)?
4.
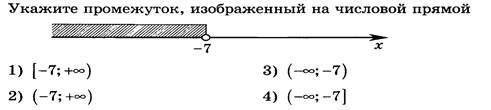
5. Какие целые числа принадлежат промежутку [-3;5]? Укажите наименьшее число [-12;-9]
Контрольная работа по теме: "Четырехугольники".
I вариант.
1. Диагонали прямоугольника MNKP пересекаются в точке О,∠MON = 64°.
Найдите угол ОМР.
2. Один из углов ромба равен 48 градусов. Найти все углы ромба.
3. Биссектриса угла прямоугольника делит его большую сторону на две части, каждая из которых равна 8 см. Найдите периметр прямоугольника.
4. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма.
5. Периметр параллелограмма равен 16 см. Чему равны стороны параллелограмма, если известно, что одна его сторона в 3 раза больше другой?
II вариант.
2. Диагонали прямоугольника ABCD пересекается в точке О,∠ABO = 36°.
Найдите угол AOD.
2. Один из углов параллелограмма равен 55 градусов. Найти все углы параллелограмма.
3.Биссектриса угла прямоугольника делит его большую сторону пополам, меньшая сторона равна 7 см. Найдите периметр прямоугольника.
4. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма.
5. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В на 40 градусов.
III вариант
3. Даны числовые промежутки А = [- 5; 7) и В = (- 4; 8]. Запишите числовые промежутки
A U В и А ∩ В, изобразите их на координатной оси.
4. Дана
функция
y = 
а) Принадлежат ли точки А(- 10; 0,1), B(- 0,5; - 2), С(- 4; - 0,25) графику этой функции?
б) Какому числовому промежутку принадлежат значения у, если x Î [- 3; - 1]?
5. Постройте график функции у = х2.
а) Докажите, что эта функция является убывающей на промежутке (-∞; 0].
б) Какому числовому промежутку принадлежат значения у, если х Î [- 5; 7]?
4*. Какому числовому промежутку принадлежат значения
выражения А =
• 
+ 
,
если а
Î 
,
если
5*.Первая, вторая и третья бригады, работая отдельно, выполнят задание за a, b и с дней соответственно, а при совместной работе они выполнят то же задание за t дней. Какому числовому промежутку наименьшей длины принадлежат значения t, если 3⩽а⩽5, 8⩽b⩽10 и 24 ⩽ с ⩽ 30?
IV вариант
1. Даны числовые промежутки А = [-6; 3) и В = (- 5; 7]. Запишите числовые промежутки A U В и А ∩ В, изобразите их на координатной оси.
2. Дана функция у = х2.
а) Принадлежат ли точки А(-11; -121), В(9; 81), С(- 12; 144) графику этой функции?
б) Какому числовому промежутку принадлежат значения у, если х Î [- 2; 6]?
3. Постройте
график функции
y = 
а) Докажите, что эта функция является убывающей на промежутке (-∞;0).
б) Какому числовому промежутку принадлежат значения у, если х Î [- 7; - 5]?
4*. Какому числовому промежутку принадлежат значения
выражения А = 
• 
,
если а
Î 
5*. Первая, вторая и третья трубы, работая отдельно, наполнят бассейн за а, b и с ч соответственно, а при совместной работе они наполнят бассейн за t ч. Какому числовому промежутку наименьшей длины принадлежат значения t, если 8 ⩽ а ⩽9, 12 ⩽ b ⩽ 18 и
24 ⩽ с ⩽ 30?
К-2
Контрольная работа № 2 по теме «Квадратные корни»
I вариант
1. Вычислите:
а)
5
+ 5(
)2
;
б) 4
- 3 
в)(
-
)2.
2. Сравните числа:
a)
и 
;
б) 
и 
.
3. Упростите:
a)
5 
+
; б)
(4 
- 
)
• 
- 4
.
4. Сократите дробь:
a)
; б) 
; в)
5*. Освободитесь от иррациональности в знаменателе дроби:
1.
; б) 
; в)
6*. На фабрике имеется два сорта чая — по 30 и по 50 р. за 1 кг. По скольку килограммов чая каждого сорта нужно взять для получения 500 кг смеси по 35 р. за 1 кг?
II вариант
1. Вычислите:
а)
6
+ 2(
)2
;
б) 8
- 3 
в)(
- 
)2.
2. Сравните числа:
a)
и 
;
б) 
и 
.
3. Упростите:
a)
3 
+ 
; б)
(2 
-
)
• 
- 2 
.
4. Сократите дробь:
; б) 
; в)
5*. Освободитесь от иррациональности в знаменателе дроби:
а)
; б) 
; в)
6*. На фабрике имеется два сорта чая — по 40 и по 60 р. за 1 кг. По скольку килограммов чая каждого сорта нужно взять для получения 400 кг смеси по 55 р. за 1 кг?
К—2
III вариант
1. Вычислите: 
– 
2. Сравните
числа: 
+ 
и 
+
.
3. Упростите выражение:
a) 3x
+
при
х≤0 и
у>0;
б)
.
4. Освободитесь от иррациональности в знаменателе дроби:
; б) 
.
5*.Докажите равенство:
+ 
= 1
6*.Имеется два сплава, содержащие по 20 и по 60% олова. По скольку килограммов каждого сплава нужно взять для получения 100 кг нового сплава, содержащего 36% олова?
IV вариант
1. Вычислите: 
– 
2. Сравните
числа: 
+ 
и 
+
.
3. Упростите выражение:
a) 5x
+
при
х
0 и
у<0;
б)
.
4. Освободитесь от иррациональности в знаменателе дроби:
; б) 
.
5*.Докажите равенство:
+ 
= 1
6*. Имеется два сплава, содержащие по 30 и по 70% олова. По скольку килограммов каждого сплава нужно взять для получения 100 кг нового сплава, содержащего 46% олова?
К—3
Контрольная работа № 3 по теме «Квадратные уравнения»
I вариант
1. Решите уравнение:
а) х2-4х- 140 = 0; б) 5х2 – 11x + 2 = 0; в) х2 – 2006x + 2005 = 0.
2. Разложите на линейные множители квадратный трехчлен 3x2-2х-1.
3. Уравнение х2+рх - 6 = 0 имеет корень 2. Найдите его второй корень и число р.
4. Пусть
хх и х2 -
корни квадратного уравнения х2 + 2х -
5
= 0. Составьте квадратное уравнение, корнями которого являются числа 
и 
.
5*. Несколько одноклассников организовали турнир по шахматам. Каждый участник турнира сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью - 1 очко, за проигрыш - 0 очков. Победитель турнира набрал 15 очков - в 5 раз меньше, чем остальные участники вместе взятые. Сколько было участников турнира?
II вариант
1. Решите уравнение:
а) х2 + 2х - 195 = 0; б) 3х2 - 7х + 2 = 0; в) х2 + 2005x - 2006 = 0.
2. Разложите на линейные множители квадратный трехчлен 2х2 + х - 3.
3. Уравнение x2-5x + q = 0 имеет корень 3. Найдите его второй корень и число q.
4. Пусть
х1 и х2 -
корни квадратного уравнения х2 -
3х
-7 = 0. Составьте квадратное
уравнение, корнями которого являются числа 
и 
.
5*. Несколько одноклассников организовали турнир по шашкам. Каждый участник турнира сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью -1 очко, за проигрыш - 0 очков. Три лучших игрока набрали вместе 44 очка - в 2 раза меньше, чем остальные участники, вместе взятые. Сколько было участников турнира?
К—3
III вариант
1. Решите уравнение:
а) х2 - 8х - 209 = 0; б) 35х2 – 12x + 1 = 0; в) 2005x2 + 2006x + 1 = 0.
2.
Для
каких значений х верно равенство 
= 
3. Уравнение х2 + рх - 8 = 0 имеет корень - 2. Найдите его второй корень и число р.
4. Пусть
х1 и х2 -
корни квадратного уравнения 3x2 –
5x+ 1 = 0. Составьте
квадратное уравнение, корнями которого являются числа 
и 
.
5*. Несколько одноклассников организовали турнир но шашкам. Каждый участник турнира сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью - 1 очко, за проигрыш - 0 очков. Пять самых слабых игроков набрали вместе 22 очка - в 4 раза меньше, чем остальные участники, вместе взятые. Сколько было участников турнира?
К—3
IV вариант
1. Решите уравнение:
а) х2 + 6х- 187 = 0; б) 32 x 2 -12 x + 1 = 0; в) 2006x2 + 2005 x -1 = 0.
2. Для каких значении х верно
равенство 
=
3. Уравнение х2 -7x + q = 0 имеет корень -3. Найдите его второй корень и число q.
4. Пусть
хх и х2 -
корни квадратного уравнения 3x2 -
4x -2
= 0. Составьте квадратное уравнение, корнями которого являются числа 
и 
.
5*. Несколько одноклассников организовали турнир по шашкам. Каждый участник турнира сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью - 1 очко, за проигрыш - 0 очков. Пять самых слабых игроков набрали вместе 26 очков - в 5 раз меньше, чем остальные участники, вместе взятые. Сколько было участников турнира?
К—4
Контрольная работа № 4 по теме «Рациональные уравнения»
I вариант
Решите уравнение (1-2):
1. а) (2 x 2- 5 x -7)(x-1) = 0; б) x 3- 9x = 0; в) x 4-7 x 2 + 6 = 0.
2.
а) 
=0; б)
= 
+ 
3. Два велосипедиста выезжают одновременно из пункта А и направляются в пункт В, удаленный от А на 90 км. Скорость первого велосипедиста на 1 км/ч больше скорости второго, поэтому первый велосипедист прибыл в B на 1 ч раньше второго. Какова скорость каждого велосипедиста?
4*.Решите уравнение (x2 – 5x)2 + 10x2 - 50x + 24 = 0.
5*. Решите уравнение х3 + ах2 - 5х + 6 = 0, если известно, что один из его корней равен 3.
II вариант
Решите уравнение (1—2):
1. а) (3x2 – 2х – 5)(х + 2) = 0; б)х3–4х = 0; в) х4–6х2+5=0.
2.
а) 
=0; б)
= 
+ 
3. Первый токарь вытачивает в час на 2 детали больше, чем второй. Поэтому он выточит 60 деталей на 1 ч раньше, чем второй токарь. Сколько деталей в час вытачивает каждый токарь?
4*. Решите уравнение (х2 + 3 x)2 – 14х2 – 42 x + 40 = 0.
5*. Решите уравнение х3 + ах2 – 5х – 6 = 0, если известно, что один из его корней равен 2.
III вариант
Решите уравнение (1—2):
1.
a) x
3-81 x
= 0; б) x 3
- 2x2
- 8
x + 16 = 0; в)
х4 -
х2 + 
= 0.
2
а)
-
=
б) 
-
= 
-
.
3. На двух станках отштамповали 1300 деталей за 13 ч. Известно, что 120 деталей на первом станке штампуют на 1 ч быстрее, чем на втором. Сколько деталей в час штампуют на первом станке?
4*. Решите уравнение x 2
–
6 x + 7 + 
=
0.
5*. Решите уравнение х3 + х2 + bх - 24 = 0, если известно, что один из его корней равен - 2.
IV вариант
Решите уравнение (1-2):
1. а)
x3 
64x=
0; б) x3
3x2
3x
+ 9 = 0; в) x4-3x2
+ 
=
0.
2
а)
-
=
б) 
-
= 
-
.
3. На двух станках отштамповали 1800 деталей за 12 ч. Известно, что 180 деталей на первом станке штампуют на 1 ч быстрее, чем на втором. Сколько деталей в час штампуют на первом станке?
4*. Решите уравнение x2
–
3x 
1
+ 
= 0.
5*.
Решите уравнение х3 
х2
+ bх
+ 24 = 0, если известно, что один из его корней равен
К—5
Контрольная работа № 5 по теме «Линейная, квадратичная и дробно-линейная функции»
I вариант
1.
Постройте
график функции: а) у =
3х;
б)
у = 2х
1.
Является ли функция возрастающей (убывающей) на множестве R?
2. Постройте график функции:
а) у = -2х2; б)
у = (х + 2)2
1.
Найдите промежутки возрастания (убывания) функции. Укажите значение х, при котором функция достигает наибольшего (наименьшего) значения.
3. График функции у = kx + l проходит через точки А(0; - 3) и В(2; 1). Найдите k и l.
4. Постройте график функции у = х2 - 6х + 5. Определите по графику, на каком числовом промежутке функция принимает отрицательные значения.
5*. Выпуская в день на 2 станка больше, чем намечено по плану, завод выпустил 80 станков за 2 дня до срока. Сколько станков в день выпускал завод?
II вариант
1. Постройте график функции: а) у = 2х; б) у =-3х + 2.
Является ли функция возрастающей (убывающей) на множестве R?
2. Постройте график функции:
а) у = - 3х2; б) у = (х1)214.
Найдите промежутки возрастания (убывания) функции. Укажите значение х, при котором функция достигает наибольшего (наименьшего) значения.
3. График функции y = kx + l проходит через точки А(0; 5) и В(2; 1). Найдите k и l.
4. Постройте график функции у = - х2+4х-3. Определите по графику, на каком числовом промежутке функция принимает положительные значения.
5*. Поезд был задержан на станции на 12 мин. Чтобы пройти участок пути в 60 км без опоздания, машинист увеличил скорость поезда на 10 км/ч. С какой скоростью шел поезд?
III вариант
1. Постройте график функции:
а) у = 
х - 2; б) у = | х2| ; в)
у = |х| 2.
С помощью определения докажите, что
функция
у =
х -
2
является
возрастающей на множестве R.
2. Постройте график функции:
а) у = - х2 + 2х + 3;
б) у = |х2
+ 2х +3|; в)
у = | -х2 + 2|х|+3|. При
каких значениях
х
значения функции
у = - х2 + 2х + 3 положительны?
3. Материальная точка движется по оси Os по закону: s = 20 t - 5t2, где s — координата точки, t — время движения (в секундах). Укажите момент времени, когда координата s точки будет наибольшей.
4*. Бригада трактористов должна была вспахать 168 га к определенному сроку. Но ежедневно бригада вспахивала на 2 га больше, чем намечено по плану, поэтому за 1 день до срока она перевыполнила задание на 14 га. Сколько гектаров в день вспахивала бригада?
5*. Постройте график функции
у = 
IV вариант
1. Постройте график функции:
а) у = х +3; б)
у = | х +3|
; в)
у = |х| +3.
С помощью определения докажите, что
функция
у =
х -
2
является
возрастающей на множестве R.
2. Постройте график функции:
а)
у = х2 4х
+ 3;
б)
у = |х2 4х
+3|;
в)
у = | х2 4|х|+3|.
При каких значениях х значения функции у = - х2 + 2х +
3 отрицательны?
3.
Материальная
точка движется по оси Os
по закону: s = 
30 t +5t2,
где
s 
координата точки,
t 
время движения (в секундах). Укажите момент времени, когда координата s
точки будет наименьшей.
4*. На середине перегона длиной 224 км поезд был задержан на 13 мин. Хотя машинист увеличил скорость поезда на 10 км/ч, в пункт назначения поезд прибыл с опозданием на 1 мин. С какой скоростью шел поезд после остановки?
5*. Постройте график функции
у = 
Контрольная работа №6 по теме «системы уравнений»
К—6
I вариант
1.
Решите систему
уравнений 
2. Решите графическим способом систему уравнений:
а)
б) 
3. При каких значениях b, с, k и l графики функций y = kx + l и у = х2 + bх + с пересекаются в точках А(6; 4) и В( 4; 10)?
4. Диагональ прямоугольника равна 10 см, а его периметр равен 28 см. Найдите стороны прямоугольника.
5*. Решите систему уравнений 
II вариант
1.
Решите систему
уравнений 
2. Решите графическим способом систему уравнений:
а)
б) 
3. При каких значениях b, с, k и l графики функций у = kx + l и у = х2 + bх + с пересекаются в точках А(- 4; 4) и В(- 6; 10)?
4. Диагональ прямоугольника равна 13 см, а его периметр равен 34 см. Найдите стороны прямоугольника.
5*. Решите систему уравнений 
III вариант
1. Решите систему уравнений 
2. Решите графическим способом систему уравнений:
а) 
б) 
3.
При
каких значениях а система уравнений 
а) имеет бесконечное множество решений;
б) имеет единственное решение?
4. Площадь прямоугольника 270 см2. Если одну его сторону увеличить на б см, а другую уменьшить на 1,5 см, то получится равновеликий ему прямоугольник. Найдите стороны первого прямоугольника.
5*. Решите систему уравнений
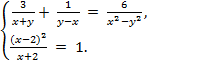
IV вариант
1. Решите систему уравнений 
2. Решите графическим способом систему уравнений:
а) 
б) 
3. При каких значениях b система уравнений
а) имеет бесконечное множество решений;
б) имеет единственное решение?
4. Площадь прямоугольника 360 см2. Если одну его сторону увеличить на 3 см, а другую уменьшить на 6 см, то получится равновеликий ему прямоугольник. Найдите стороны первого прямоугольника.
5*. Решите систему уравнений
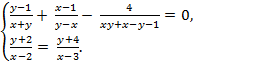
Итоговая контрольная работа №7 по теме «Повторение курса математики 8 класса»
К—7 Данная контрольная работа рассчитана на 2 ч.
I вариант
1.
Докажите,
что число 
является
рациональным.
2.
Найдите
наибольшее значение квадратного трехчлена 
-
х2 
6х 
8.
2х у = 1,
3. Решите систему уравнений 
4. Решите
графическим способом уравнение 
= х+1.
5. Катер, скорость которого в стоячей воде 15 км/ч, отправился от речного причала вниз по течению и, пройдя 36 км, догнал плот, отправленный от того же причала за 10 ч до отправления катера. Найдите скорость течения.
6*. Найдите наименьшее значение функции
у = 6 
.
II вариант
1.
Докажите,
что число 
является
рациональным.
2.
Найдите
наибольшее значение квадратного трехчлена х2 
4х +2.
3. Решите систему уравнений 
4. Решите
графическим способом уравнение 
= х+2.
5. Турист, проплыв по течению реки на плоту 12 км, возвратился обратно на лодке, скорость которой в стоячей воде 6 км/ч. Найдите скорость течения реки, если известно, что на все путешествие турист затратил 8 ч.
6*. Найдите наименьшее значение функции
у = 5 + 
.
III вариант
1.
Докажите,
что число 
является рациональным.
2.
Найдите
наибольшее значение квадратного трехчлена х2 
4х +2.
3. Решите систему уравнений 
4. Решите
графическим способом уравнение 
= |х
1|.
5. Турист, проплыв по течению реки на плоту 16 км, возвратился обратно на лодке, скорость которой в стоячей воде 6 км/ч. Найдите скорость течения реки, если известно, что на все путешествие турист затратил 12 ч.
IV вариант
1.
Докажите,
что число 
является рациональным.
2.
Найдите
наибольшее целое значение квадратного трехчлена 
2х2 + 3х
+ 7.
3.
Решите
систему уравнений 
4. Решите
графическим способом уравнение 
= |х
2|.Турист,
проплыв по течению реки на плоту 12 км, возвратился обратно на лодке, скорость
которой в стоячей воде 5 км/ч. Найдите скорость течения реки, если известно,
что на все путешествие турист затратил 10 ч.
1. Арифметический квадратный корень
Теория:
Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен данному числу a.
Обозначается: a−−√.
Читается: квадратный корень из a.
Число a называется подкоренным числом.
16−−√=4,т. к.42=16.
Обрати внимание!
Квадратный корень из отрицательных чисел не существует.
Например, −16−−−−√ не имеет смысла, т. к. нет такого действительного числа a, которое в квадрате равно отрицательному числу: a2≠−16.
Чтобы найти квадратный корень из числа, необходимо хорошо знать квадраты чисел.
Часто используемые квадраты целых чисел:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
25 |
|
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
400 |
625 |
Значит, 81−−√=9;121−−−√=11;361−−−√=19и т. д.
Обрати внимание!
1–√=1;0–√=0.
Если подкоренное число — десятичная дробь, то необходимо обращать внимание на количество цифр после запятой:
0,09¯¯¯¯−−−−√=0,3¯,т.к.0,32=0,3⋅0,3=0,09;0,0016¯¯¯¯¯¯¯−−−−−−√=0,04¯¯¯¯;0,009−−−−√=?
Устно вычислить невозможно, т. к. результатом является бесконечная десятичная дробь.
Если подкоренное число заканчивается нулями, то необходимо обращать внимание на их количество:
400¯¯¯¯−−−√=20¯;1210000¯¯¯¯¯¯¯−−−−−−−√=1100¯¯¯¯;9000¯¯¯¯¯−−−−√=?
Устно вычислить невозможно, т. к. результатом является бесконечная десятичная дробь (проверь с помощью калькулятора).
Если выражение a−−√ имеет смысл, то a−−√≥0и(a−−√)2=a.
(8–√)2=8;(16−−√)2=16, нерационально сначала извлекать корень из 16, а затем результат возводить в квадрат.
СТИХИ О ГЕРМАНИИ 2001-2002
Берусь за перо с опаской:
а ждёт ли меня успех?
Германия - это сказка,
любимейшая из всех.
Пьянят, как бокал глинтвейна,
как взоры прекрасных дам,
и синие воды Рейна,
и замки по берегам.
Согрет под баварским солнцем,
не знающий про мороз,
там терпкой струею льётся
дар виноградных лоз.
А лик городов так чуден,
дома так сказочны тут,
что кажется, в них не люди -
волшебные гномы живут.
Твоих крепостей и башен,
твоих черепичных крыш
не кажутся даже краше
ни Рим, ни Мадрид, ни Париж.
Сладка, как любовная ласка,
влюбиться в тебя не грех -
Германия - это сказка,
любимейшая из всех.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
