Контрольная работа по "Вероятности и статистике" для 10 класса

ВиС - 10         Контрольная работа №2

Вариант 1

1. Семён гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что таким образом он выйдет к памятнику или к пруду.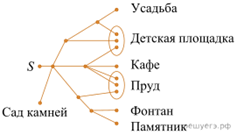

2. 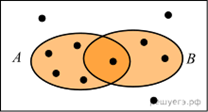 На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите — условную вероятность события B при условии A.

3. 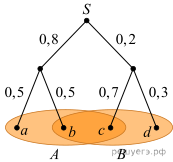На рис. показано дерево некоторого случайного эксперимента. Событию A благоприятствуют элементарные события a, b и c, а событию B благоприятствуют элементарные события b, c и d. Найди  — условную вероятность события A при условии B.

4.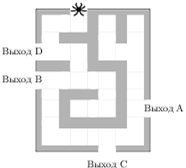 На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу D.

5. В го­ро­де 42 % взрос­ло­го на­се­ле­ния  — муж­чи­ны. Пен­си­о­не­ры со­став­ля­ют 9,2 % взрос­ло­го на­се­ле­ния, причём доля пен­си­о­не­ров среди жен­щин равна 5 %. Для со­цио­ло­ги­че­ско­го опро­са вы­бран слу­чай­ным об­ра­зом муж­чи­на, про­жи­ва­ю­щий в этом го­ро­де. Най­ди­те ве­ро­ят­ность со­бы­тия «вы­бран­ный муж­чи­на яв­ля­ет­ся пен­си­о­не­ром».(0,15)

6. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810 г, равна 0,97. Вероятность того, что масса окажется больше, чем 790 г, равна 0,91. Найдите вероятность того, что масса буханки больше, чем 790 г, но меньше, чем 810 г.

7. Прибор может работать в двух режимах: нормальном и ненормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора, а ненормальный - в 20% случаев. Вероятность выхода прибора из строя за определённое время t равна 0,1; в ненормальном 0,7. Найти полную вероятность выхода прибора из строя за время t.

Решение 5. Пусть х  — доля мужчин-пенсионеров среди всех мужчин. Построим дерево вероятностей (см. рис.).

Пенсионеры составляют 0,092 взрослого населения города, откуда получаем:

Т.о., вероятность того, что случайно выбранный мужчина окажется пенсионером, равна 0,15.

Решение 6. Пусть событие А состоит в том, что масса буханки меньше, чем 810 г, а событие B состоит в том, что масса буханки больше, чем 790 г. Необходимо вычислить вероятность произведения этих событий. Сумма этих событий является событием достоверным, его вероятность равна 1. В то же время Р(А+В)=Р(А) + Р(В) – Р(АВ) поскольку события A и B совместные. Подставляя известные значения, находим искомую вероятность:

Р(А+В)=Р(А) + Р(В) – Р(АВ) = 0,97 + 0,91 - 1 = 0,88    Ответ: 0,88.

Решение 7. Вновь обозначаем вероятность выхода прибора из строя через A. Итак, относительно работы прибора в каждом режиме (события В₁, В₂) по условию известны вероятности: для нормального режима это 80% (Р(В₁) = 0,8), для ненормального - 20% (Р(В₂) = 0,2). Вероятность события A (то есть, выхода прибора из строя) в зависимости от первого события (нормального режима) равна 0,1 (Р(В₁|А) = 0,1); в зависимости от второго события (ненормального режима) - 0,7 (Р(В₂|А) = 0,7). Подставляем эти значения в формулу полной вероятности (то есть, сумму произведений вероятности каждого из событий системы на условную вероятность события A относительно каждого из событий системы) и перед нами - требуемый результат: Р(А) = 0,8·0,1 + 0,2·0,7 = 0,22  .