Конвективний теплообмін

3.4. Конвективний теплообмін

     3.4.1. Загальні положення.

     Конвективний теплообмін має винятково важливе значення в хімічній технології, оскільки від того, як здійснюється підведення або відведення теплоти, часто залежить і сама можливість проведення хіміко-технологічних процесів. У реальних умовах конвекція завжди супроводжується теплопровідністю (а іноді й тепловим випромінюванням). Під конвективним теплообміном розуміють процес поширення тепла в рідині (газі) від поверхні твердого тіла або до його поверхні одночасно конвекцією й теплопровідністю. Такий випадок поширення тепла називають також конвективною тепловіддачею. При тепловіддачі тепло поширюється від поверхні твердого тіла до рідини через пограничний шар за рахунок теплопровідності й від пограничного шару в масу (ядро) рідини переважно конвекцією. Очевидно, що на тепловіддачу істотний вплив має характер руху рідини.

     Вільний рух рідини (вільна або природна конвекція) виникає внаслідок різниці густини нагрітих і холодних часток рідини й визначається фізичними властивостями рідини, її об’ємом і різницями температур нагрітих і холодних часток.

     Вимушений (примусовий) рух рідини (вимушена конвекція) виникає під дією якого-небудь зовнішнього впливу (насоса, вентилятора, мішалки і т.ін.) і визначається фізичними властивостями рідини, її швидкістю, формою й розмірами каналу, у якому здійснюється рух.

     Тепловіддачу, як і конвекцію, підрозділяють на вільну (природну) і вимушену (примусову).

     3.4.2. Основне рівняння й коефіцієнт тепловіддачі.

     Конвективний перенос тепла має місце тільки в рухливих середовищах. На відміну від теплопровідності перенос теплової енергії в просторі в цьому випадку здійснюється не тільки за допомогою мікроструктурних елементів (молекул, атомів), а головним чином макроскопічними об’ємами речовини (рідини, газу), що рухаються.

     Процес конвективного теплообміну, його кількісні показники залежать від режиму руху теплоносія, його фізичних властивостей, геометрії апарату й стану поверхні теплообміну.

     При розгляді гідродинамічної структури потоку було встановлено, що при обтіканні твердого тіла рідиною (газом) уздовж його поверхні утворюється особливий пограничний шар рідини. Якщо потік рідини, що омиває стінку, постійний і має ламінарний характер, то структура пограничного шару залишається незмінною на всьому протязі стінки. При цьому тепло від стінки в ядро потоку(або навпаки), у нормальному до стінки напрямку, передається в основному теплопровідністю. Конвективний перенос тепла тут має місце лише в напрямку потоку.

     У більшості випадків у промислових теплових апаратах режим руху рідини має турбулентний характер, оскільки при турбулентному русі рідини теплообмін проходить значно інтенсивніше, ніж при ламінарному. При такому русі основної частини потоку ламінарний пограничний шар на деякій відстані від краю стінки також починає відчувати імпульси, що приводить до турбулентного руху значної товщини пограничного шару. Ступінь турбулізації пограничного шару буде тим більше, чим більше величина Rе потоку. Однак вважається, що навіть при добре розвиненому турбулентному русі рідини, в безпосередній близькості від стінки все-таки залишається тонкий ламінарний підшар, через який перенос тепла по нормалі до стінки здійснюється теплопровідністю, а за його межами - конвекцією.

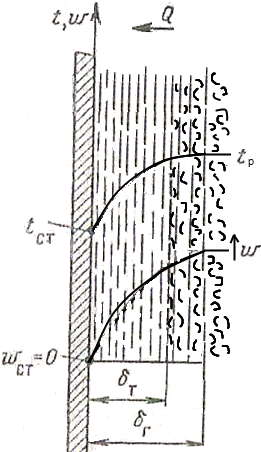
     Наявність гідродинамічного пограничного шару  δ_г поблизу поверхні стінки приводить до виникнення в ньому великого перепаду температур при теплоперенесенні  (рис 3.6), тобто утворення теплового пограничного шару δ_т, значення якого звичайно не збігається з товщиною гідродинамічного пограничного шару δ_г. Очевидно, що високі швидкості теплоносія, інтенсивне перемішування викликають руйнування пограничних шарів, поліпшуючи тим самим умови тепловіддачі.

    Теоретично товщину пограничного теплового шару можна розрахувати тільки для найпростіших випадків теплоперенесення. Тому використання рівняння

теплопровідності Фур'є (3.7) для опису процесу є досить складним, оскільки невідомий закон розподілу температури  у пограничному шарі.

Рис. 3.6. Гідродинамічний і тепловий пограничні шари в

турбулентному потоці

     Звичайно розрахунок швидкості процесу конвекційної тепловіддачі здійснюють за допомогою емпіричного закону  Ньютона-Ріхмана, який  у подальшому будемо називати рівнянням тепловіддачі:

                        (3.18)

     Відповідно, густина теплового потоку

                            (3.18a)

У цих рівняннях α - коефіцієнт пропорційності (кінетичний коефіцієнт) або коефіцієнт тепловіддачі, ,  - температура відповідно в ядрі потоку рідини (теплоносія) і на поверхні стінки.

     При сталому процесі для всієї поверхні тепловіддачі F рівняння (3.18) приймає вид:

                                       (3.19)                                                     

     Знайдемо розмірність коефіцієнта тепловіддачі:

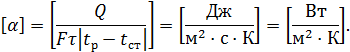
     Таким чином, коефіцієнт тепловіддачі показує, яка кількість теплоти передається від теплоносія до 1 м² поверхні стінки (або від стінки поверхнею 1 м² до теплоносія) в одиницю часу при різниці температур між теплоносієм і стінкою 1 град. На відміну від коефіцієнта К коефіцієнт тепловіддачі α характеризує швидкість переносу теплоти в теплоносії.

     Порівнюючи рівняння (3.7) і (3.18), одержимо вираження для коефіцієнта тепловіддачі

                                            (3.20)

     Метою рішення завдань конвекційного теплообміну є визначення для кожного конкретного випадку величини коефіцієнта тепловіддачі α, що є функцією фізичних параметрів рідини, швидкості й характеру її течії, форми й розмірів теплообмінної поверхні, температурного напору й ін.

     Багатофакторна залежність коефіцієнта тепловіддачі утруднює його теоретичне визначення. Навіть для однакових умов процесу тепловіддачі, коливання значень α досить значні й становлять (Вт/(м²К)):

     У практиці для визначення коефіцієнта тепловіддачі звичайно використовують експериментальний метод. Дослідне визначення коефіцієнта тепловіддачі в основному проводять не на теплових установках безпосередньо, а на їхніх спрощених моделях. Отримані на моделях експериментальні результати узагальнюються за допомогою теорії подібності. Переваги цієї теорії полягають у тому, що вона виключає необхідність визначати залежність α від кожного фактора, що впливає на нього. Для вирішення задачі досить знайти залежність між певними комплексами величин, характерними для розглянутих умов процесу тепловіддачі. Ці комплекси називаються критеріями, або числами теплової подібності. Одержують критерії теплової подібності з диференціальних рівнянь теплообміну, які встановлюють залежності між параметрами процесу в диференціальній формі.

     3.4.3. Диференціальні рівняння конвективного теплообміну.

     Процес переносу тепла на границі рідини з поверхнею твердого тіла може бути виражений законами Фур'є (3.7) і Ньютона-Ріхмана (3.20). Дорівнявши праві частини цих рівнянь, одержимо диференціальне рівняння тепловіддачі, що характеризує умови теплообміну на границі (граничні умови)

                                            (3.21)

     У потоці за межами пограничного шару тепло передається одночасно як теплопровідністю, так і конвекцією. Поширення тепла теплопровідністю в елементарному об’ємі середовища описується диференціальним рівнянням теплопровідності

                                       (3.22)

     Це рівняння характеризує місцеву (локальну) зміну температури елемента середовища й не враховує зміни температури в ньому при конвективному переносі елемента з однієї точки об’єму в іншу з більшою або меншою температурою.

      Якщо швидкість конвективного переміщення елемента середовища щодо осей х, у, z, позначити w_x, w_y, w_z, а зміну його температури при русі щодо осей відповідно , , , то конвективна зміна температури розглянутого елемента буде виражатися сумою

.

     Отже, повна зміна температури елементарного об’єму середовища Dt/Dτ буде складатися з локального ∂t/∂τ й конвективного:

     Замінивши в рівнянні (3.22) локальну зміну температури повною, одержимо диференціальне рівняння конвективного теплообміну (рівняння Фур’є – Кірхгофа)

                             (3.23)

або      

                                   (3.23a)

     Це рівняння є математичним описом процесу розповсюдження тепла в рухомому середовищі одночасно теплопровідністю і конвекцією. Для повного математичного опису процесу конвективного теплообміну воно повинно бути доповнене рівнянням (3.21), яке характеризує умови на границі розділу рухомого середовища і твердого тіла.

     Рішення кожної конкретної задачі конвективного теплообміну полягає в інтегруванні диференціальних рівнянь із урахуванням певних заданих умов. Такі аналітичні рішення здійсненні лише для порівняно простих задач. Для більшості ж випадків цей метод не можна застосувати через математичні труднощі аналітичного рішення.

     3.4.4. Подібність процесів тепловіддачі

       Для повного опису конвективного перенесення теплоти необхідно приєднати до рівняння Фур’є-Кірхгофа рівняння руху рідини Нав’є-Стокса, рівняння нерозривності потоку й алгебраїчні рівняння, що описують залежність фізичних властивостей рідини від температури. Аналітичні рішення основних задач тепловіддачі розроблені для ламінарних потоків рідини різної форми. Для турбулентних потоків одержати аналітичні рішення значно складніше у  зв'язку з незавершеністю теорії турбулентності.

     Тому в загальному випадку залежності для розрахунку швидкості процесу тепловіддачі одержують перетворенням диференціальних рівнянь, що описують цей процес, за методом теорії подібності.

     Розглянемо спочатку подібність граничних умов. Як вказувалося раніше, при турбулентному русі рідини тепло біля границі потоку, тобто в безпосередній близькості до твердої стінки, передається теплопровідністю через пограничний шар у напрямку, перпендикулярному напрямку руху потоку. Отже, за законом Фур'є [рівняння(3.7)] кількість тепла, що проходить у пограничному шарі товщиною δ через площу перерізу dF за час dτ, становить  

                                                                      (А)

Кількість тепла, що проходить від стінки в ядро потоку, визначається за рівнянням тепловіддачі (3.18):

                                               (Б)

     При сталому процесі теплообміну кількості тепла, що проходять через пограничний шар і ядро потоку, рівні. Тому, дорівнюючи вираження (А) і (Б) й скорочуючи подібні члени, одержимо

     =                                       (3.24)

     Для подібного перетворення цього рівняння розділимо (див. п. 1.4.1) його праву частину на ліву й відкинемо знаки математичних операторів. При цьому величину δ замінимо деяким визначальним геометричним розміром l . Тоді одержимо безрозмірний комплекс величин

                                                        (3.25)

який називається критерієм Нуссельта. Критерій Нуссельта є основним критерієм конвективного теплообміну і характеризує подібність процесів теплопереносу на границі між стінкою й потоком рідини. На основі спільного розгляду рівнянь (А) і (Б) можна показати, що Nu є мірою співвідношення товщини пограничного шару δ і визначального геометричного  розміру l (для труби - її діаметр d).

      Тепер розглянемо умови подібності в  ядрі потоку, використовуючи подібне перетворення рівняння (3.23). У лівій частині рівняння Фур’є-Кірхгофа сума членів, що визначають вплив швидкості потоку на теплообмін, може бути замінена пропорційною їй величиною:

де l - визначальний лінійний розмір.

     Праву частину того ж рівняння, що характеризує перенос тепла шляхом теплопровідності, також замінимо відповідною пропорційною величиною:

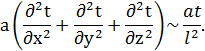
     Член , що характеризує несталість режиму теплообміну, може бути замінений відношенням t/τ.

     Виразимо всі члени рівняння (3.23) у відносних одиницях, прийнявши за масштаб кількість тепла, що передається шляхом теплопровідності. Розділивши член t/τ на at/l², одержимо безрозмірний комплекс величин l²/aτ. Цей комплекс звичайно заміняють на зворотну величину для того, щоб у розрахунках не оперувати із дробовими числами. Останній комплекс зветься критерієм Фур'є:

                                                 (3.26)

Рівність критеріїв Фур'є в подібних точках теплових потоків - необхідна умова подібності несталих процесів теплообміну. Критерій Фур'є є аналогом критерію гомохронності Ho при гідродинамічній подібності.

     Розділивши конвективний член  на  й зробивши необхідні скорочення, одержимо

                                                (3.27)

     Цей безрозмірний комплекс величин називається критерієм Пеклє. Він, як випливає з проведеного подібного перетворення, є мірою співвідношення між теплом, що переноситься шляхом конвекції й шляхом теплопровідності при конвективному теплообміні.

     Необхідними умовами подібності процесів переносу тепла є, крім того, дотримання гідродинамічної й геометричної подібності. Перше характеризується  рівністю критеріїв Но, Rе й Fr у подібних точках подібних потоків, а друге — сталістю відношень основних геометричних розмірів стінки l₁, l₂, …, l_п до деякого характерного розміру l₀.

      Для труб характерним розміром звичайно є їхній діаметр (l₀ = d). Крім того, в деяких випадках за l₀  можуть бути прийняті також довжина труби, радіус кривизни вигнутої труби й т.д.

     Таким чином, узагальнене (критеріальне) рівняння конвективного теплообміну виражається функцією виду

                     (3.28)

або з урахуванням того, що критерій Нуссельта є визначуваним, оскільки в нього входить шукана величина коефіцієнта тепловіддачі α:

                       (3.29)

     Критерій Пеклє може бути представлений як добуток двох безрозмірних комплексів:

     Безрозмірний комплекс

                                         (3.30)

називається критерієм Прандтля. Він цілком складений з величин, що виражають фізичні властивості рідини, і характеризує подібність фізичних властивостей теплоносіїв у процесах конвективного теплообміну. Критерій Рr є мірою подібності полів температур і швидкостей.

     Значення критерію Прандтля для краплинних рідин знаходиться в межах 3÷300 і значно зменшуються зі зростанням температури, а для газів постійні (Рr≈0,7÷1) й залежать від атомності газу. Тому для рідин тепловий підшар тонший за гідродинамічний.

     Із введенням критерію Рr узагальнене рівняння конвективного теплообміну приймає вид

                    (3.31)

     При сталому процесі теплообміну з узагальненого рівняння виключаються критерії Fо й Но. При вимушеному русі, коли вплив сил ваги на гідродинаміку потоку, який віддає або сприймає тепло, є незначним, впливом критерію Fr на тепловіддачу можна знехтувати. Тоді

                               (3.32)

     Вид функцій (3.31), (3.32) визначається дослідним шляхом, причому звичайно їм надають степеневу форму. Так, наприклад, рівняння (3.32) при русі потоку в трубі діаметром d і довжиною l може бути представлене у вигляді

                                (3.33)

де С, m, n, p - величини, що визначаються з дослідів.

     При тепловіддачі в умовах природної конвекції в число визначальних критеріїв повинен увійти критерій Фруда, що характеризує дію сил ваги в подібних потоках (Fr = w²/gl). Однак, через труднощі визначення швидкості при природній конвекції, критерій Фруда доцільно замінити для даних умов на похідні критерії. Наприклад, швидкість можна виключити шляхом сполучення критеріїв Re і Fr:

–критерій Галілея.

      Шляхом множення цього критерію на відносну різницю густини в різних точках об’єму рідини одержують критерій Архімеда

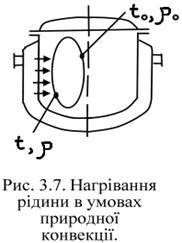
     Якщо процес теплообміну протікає в умовах природної конвекції, тобто вільного руху, обумовленого різницею густини нагрітих і холодних елементарних об’ємів рідини, їхня різниця густини Δρ і підйомна сила, що виникає при русі часток, визначаються температурним напором Δt. Тому величину Δρ можна замінити пропорційною величиною Δt.

     Якщо нерухома рідина нагрівається в апараті без примусового перемішування (рис. 3.7), то для будь-яких двох часток, що перебувають на різній відстані від стінки, через яку передається тепло, t>t₀ й ρ<ρ₀. Залежність між рушійною силою природної конвекції, обумовленою різницею густини Δρ, і її вираженням через різницю температур має вигляд

Δρ = ρ₀ – ρ = ρ₀ - ρ₀(1-βΔt) = ρ₀βΔt.

     Підставляючи в критерій Аr значення Δρ = ρ₀βΔt і скорочуючи ρ₀, одержуємо вираження нового критерію - критерію Грасгофа:

                                              (3.34)

де β - коефіцієнт об'ємного розширення рідини, 1/град; Δt - різниця температур між стінкою й рідиною (або навпаки), якою визначається різниця густин  рідини, град; l - визначальний геометричний розмір (для труби - її діаметр, для вертикальної плоскої стінки - її висота).

     Таким чином, критерій Gr є, подібно критеріям Галілея (Gа) і Архімеда (Аr), аналогом критерію Фруда. Критерій Gr являє собою визначальний критерій теплової подібності при природній конвекції, коли рух рідини цілком обумовлений самим процесом теплообміну. Критерій Грасгофа можна розглядати як міру відношення сил тертя до підйомної сили, обумовленої різницею густин у різних точках неізотермічного потоку.

     Отже, для процесів тепловіддачі при природній конвекції, або вільному русі рідини, узагальнене рівняння тепловіддачі може бути представлене у вигляді

                                        (3.35)

     Для газів Pr≈1=const  і тому критерій Рr можна виключити з узагальнених рівнянь для визначення α.

     Усі члени критеріальних рівнянь містять фізичні константи рідин, які залежать від температури, що змінюється по ходу процесу. Для спрощення інженерних розрахунків введено поняття так званої визначальної температури  t_визн, за якою знаходять всі фізичні константи. Величина t_визн не має універсального значення, а вибирається при побудові розрахункових рівнянь виходячи з кращого їх узгодження з дослідними даними. Найчастіше за визначальну приймають або середньоарифметичну температуру потоку рідини t_р, або середню температуру поверхні стінки, що омивається рідиною, t_ст, або середньоарифметичну температуру між  t_р та t_ст. В критерії  Nu, Re, Fr, Ar, Gr та ін. входить також визначальний розмір потоку l_визн – лінійний розмір, який найбільш повно характеризує систему, в якій протікає процес. Таким розміром при русі рідини в трубах круглого перерізу є внутрішній діаметр труби, а при поперечному їх обтіканню – зовнішній діаметр, при русі в каналах любих інших перерізів – еквівалентний діаметр d_е (збільшена учетверо площа поперечного перерізу, поділена на змочений периметр), при обтіканні плити – її довжина по напрямку потоку. Визначальні температура і розмір обов’язково вказуються в розрахункових рівняннях.

      Крім того, слід зазначити, що формули для розрахунку коефіцієнтів конвекційної тепловіддачі базуються на дослідах, проведених у визначених діапазонах робочих умов, тому границі їх надійного застосування обмежені цими діапазонами, які також обов’язково вказуються.      

      Розрахункові рівняння для абсолютної більшості розповсюджених в хімічній технології випадків тепловіддачі, отримані шляхом узагальнення дослідних даних, наводяться в спеціальній літературі і класифікуються приблизно наступним чином:

     Узагальнюючи вищевикладене, можна відзначити, що на коефіцієнт тепловіддачі впливають наступні визначальні фактори:

1.     Характер руху теплоносія і його швидкість. При турбулентному режимі із збільшенням швидкості теплоносія товщина пограничного шару зменшується і відповідно α збільшується.

2.     Фізичні властивості теплоносія (в’язкість, теплопровідність, теплоємність, густина і т.ін.). Коефіцієнт тепловіддачі збільшується із зменшенням в’язкості і збільшенням λ, ρ, с. Оскільки фізичні властивості рідин і газів змінюються при зміні температури, то, відповідно, значення α залежить і від температури.

3.     Розміри і форма поверхні теплообміну, її оброблення (гладка, шорстка і т.ін.).

     Методика розв’язання задач конвективного теплообміну на основі теорії подібності полягає в наступному:

1.    Визначають умови протікання процесу (тепловіддача супроводжується зміною агрегатного стану чи ні, наявність теплового випромінювання, конвекція вільна чи вимушена, геометрія та режим течії і т. ін.).

2.    Розраховують значення основних визначальних критеріїв і, відповідно до умов протікання процесу, визначають критеріальне рівняння процесу та розраховують критерій Nu.

3.    Розраховують коефіцієнт тепловіддачі:

4.    Використовуючи рівняння Ньютона-Ріхмана визначають кількість переданого тепла або іншу невідому величину.