Корни натуральной степени из числа и их свойства. Действия с корнями. Арифметический корень.

Лекция № 4

Тема: Корни натуральной степени из числа и их свойства. Действия с корнями. Арифметический корень.

Количество часов: 2 часа

Цель: формирование у обучающихся целостного представления о корне n- ой степени, навыков сознательного и рационального использования свойств корня при решении различных задач; способствовать развитию алгоритмического, творческого мышления

План:

1.       Корень степени n. Корни четной и нечетной степени.

2.       Действия с корнями.

3.       Арифметический корень.

Вопрос 1. Корень степени n, его свойства.

Первые задачи, связанные с извлечением квадратного корня, обнаружены в трудах вавилонских математиков Среди таких задач:

·            Применение теоремы Пифагора для нахождения стороны прямоугольного треугольника по известным двум другим сторонам.

·            Нахождение стороны квадрата, площадь которого задана.

·            Решение квадратных уравнений.

Определение 1.Корнем n-й степени из неотрицательного числа а (n = 2, 3,4, 5,...) называют такое неотрицательное число, которое при возведении в степень n дает в результате число а.

Это число обозначают, число а при этом называют подкоренным числом, а число n — показателем корня.

Если n=2, то обычно не говорят «корень второй степени», а говорят «корень квадратный». В этом случае не пишут , а пишут . Это тот частный случай, который вы специально изучали в курсе алгебры 8-го класса.

Если n = 3, то вместо «корень третьей степени» часто говорят «корень кубический».

Итак,

если , n = 2, 3, 4, 5, …, то: 1)  ;       2) 

Операцию нахождения корня из неотрицательного числа называют обычно извлечением корня. Эта операция является обратной по отношению к возведению в соответствующую степень.

Например,

Операцию извлечения корня определяют и для отрицательного подкоренного числа, но только в случае нечетного показателя корня.

Определение 2.Корнем нечетной степени n из отрицательного числа а (n = 3,5,...) называют такое отрицательное число, которое, будучи возведено в степень n, дает в результате число а.

Это число, как и в определении 1, обозначают , число а — подкоренное число, число n — показатель корня.

Итак,

если , n = 3, 5, 7, …, то: 1)  ;       2) 

Например,

Таким образом, корень четной степени имеет смысл (т.е. определен) только для неотрицательного подкоренного выражения; корень нечетной степени имеет смысл для любого подкоренного выражения.

Вопрос 2.Действия с корнями.

1. Величина корня не изменится, если его показатель увеличить в n раз и одновременно возвести подкоренное выражение в степень n

2. Величина корня не изменится, если показатель степени уменьшить в n раз и одновременно извлечь корень n – й степени из подкоренного выражения:

3. Корень из произведения нескольких сомножителей равен произведению корней той же степени из этих сомножителей:

Обратно, произведение корней одной и тойже степени равно корню той же степени из произведения подкоренных выражений:

4. Корень из частного равен частному от деления корня из делимого на корень из делителя (показатели корней подразумеваются одинаковыми):

Обратно:

5. Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное выражение:

Обратно, чтобы извлечь корень из степени, достаточно возвести в эту степень корень из основания степени:

Вопрос 3. Арифметический корень.

Корень называется арифметическим, если он извлекается из положительного числа и сам представляет собой положительное число.

Например,

Арифметический корень данной степени из данного числа может быть только один.

Свойства арифметических корней

1)      Чтобы извлечь арифметический корень из произведения, можно извлечь его из каждого сомножителя отдельно

Например,

2)Чтобы извлечь корень из дроби, можно извлечь его из числителя и знаменателя отдельно

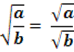
Например,

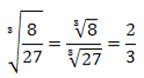
3)Чтобы извлечькорень из степени,  можно разделить показатель степени на показатель корня

Например,

Вопросы для самопроверки:

1.     Дайте определение корню степени n.

2.     Перечислите действия с корнями.

3.     Дайте определение арифметическому корню.

4.     Какими свойствами обладает арифметический корень?

Список литературы и ссылки на Интернет-ресурсы, содержащие информацию по теме:

1.       Башмаков М.И., Математика: учебник для студ. учреждений сред. проф. образования / М.И. Башмаков. – 7-е изд., стер. - М: Издательский центр «Академия», 2020. - 256с.

2.       Григорьев С.Г. Математика: учебник для студ. учреждений сред. проф. организация/ С.Г.Григорьев, С.В.Иволгина; под ред. В.А.Гусева. – 14-е изд., стер. – М.: Издательский центр «Академия», 2019. – 416 с.

3.       Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни – 5-е изд. -  М.: Просвещение, 2018. – 431 с.: ил.

Скачано с www.znanio.ru