Корреляционно- регрессионный анализ

Корреляционно- регрессионный анализ

В экономических исследованиях чаще встречаются стохастические зависимости, ко­торые отличаются приблизительностью, не­определенностью.  Каждой ве­личине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функции).

            Установить наличие связи между такими показателями, оценить ее тесноту, установить вид зависимости позволяет корреляционно-регрессионный анализ.

Отличают парную и множественную корреляцию.   

Парная корреляция - это связь между двумя показателями, один из которых является факторным, а другой - результативным. Множественная корреляция возникает от взаимодействия не­скольких факторов с результативным показателем.

Парная корреляция.

Анализ состоит из следующих этапов:

1.     Построение поля корреляции.

2.  Построение эмпирической линии регрессии.

3.  Установление  вида зависимости и построение теоретической линии регрессии.

           В общем виде зависимость результирующего показателя от факторного показателя может быть представлена как:    Y = f (x)

Если предположить, что имеет место линейный вид зависимости:

Y = abx,

       где  a, b - коэффициенты регрессии, то для построения теоретической линии регрессии необходимо рассчитать эти коэффициенты по следующим формулам.

;                             .

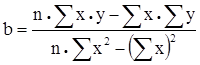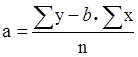4. Установление тесноты связи (по коэффициенту корреляции).

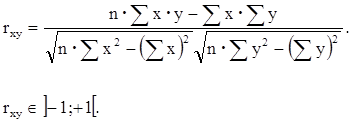
            Чем ближе значение r_xy к границам, тем связь теснее.

 Знак при коэффициенте корреляции:

       ’’-’’   - свидетельствует об обратной связи между показателями, т.е. при увеличении значения X уменьшается значение Y;

       ’’+’’- свидетельствует о прямой связи между показателями, т.е. при увеличении значения X увеличивается значение Y.

5. Количественная оценка влияния факторов.

            Коэффициент регрессии при X показывает на сколько изменится Y при изменении X на единицу измерения.

Множественная корреляция.

Результирующий показатель зависит от ряда факторных показателей:

Y = f (x₁,x₂, ... , x_n),

где Y – результативный показатель; x₁, x₂, ..., x_n - признаки-факторы.

Уравнение множественной регрессии:

У = a₀ + a₁x₁ + a₂x₂ + a _ix _i +a _nx _n,

            где a₁ ... a_n - коэффициенты множественной регрессии.

            Коэффициенты регрессии при х₁ ... х_n   показывают как изменится результирующий показатель, если соответствующий фактор изменится на единицу измерения.

Свободный член а₀  характеризует влияние неучтенных факторов на результирующий показатель.

Совокупный коэффициент корреляции учитывает влияние одновременно нескольких факторов-аргументов и характеризует тесноту связи между функциональным и факторными признаками.

Коэффициент множественной детерминации (R²) - показывает какая часть вариации результирующего признака осуществляется за счет вариации линейной комбинации факторов-аргументов.

            Например: R = 0,968,           R² = 0,937.

            Это означает, что на 93,7 % вариация результирующего признака зависит от вариации выбранных факторов-признаков.