Курсовая работа "Операции над графами"

Государственное автономное профессиональное образовательное учреждение

Владимирской области

«Гусь-Хрустальный технологический колледж» им. Г.Ф. Чехлова

(ГАПОУ ВО «ГХТК»)

 

Специальность 09.02.02 Компьютерные сети

 

Курсовая работа

по МДК 01.02.  «Математический аппарат для построения компьютерных сетей»

На тему: Операции над графами

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Гусь-Хрустальный, 2019

 

 

Содержание

 

 

 

ВВЕДЕНИЕ

 

 

Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г. Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики и особенно её приложений дало сильный толчок развитию теории графов. Уже в XIX столетии графы использовались при построении схем.

Актуальность заключается в том, что теория графов находит многочисленное применение в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сети нефтепроводов, в программировании и теории игр, теории передачи сообщений. Теория графов теперь применяется и в таких областях, как экономика, психология и биология.

Цель курсовой работы: дать подробную характеристику операций над графами.

Объект: графы.

Предмет: операции над графами.

Для достижения поставленной цели ставятся следующие задачи:

- дать определение понятию граф;

- изучить основные понятия теории графов;

- рассмотреть способы представления графов;

- рассмотреть классификацию операций над графами;

- описать бинарные операции;

- описать унарные операции.

Методологической базой для написания работы послужили общенаучные методы исследования: обобщения, анализа и синтеза, систематизации, а также изучение научной и учебной литературы, технических справочников, самоучителей, материалы различных Интернет-ресурсов.

Курсовая работа состоит из введения, трех разделов, заключения и списка используемых источников. Первый раздел посвящен основным понятиям теории графа, тут же рассмотрены основные виды графов. Во втором разделе рассмотрены способы представления графов. В третьем разделе приведена классификация операций над графами, в частности бинарные и унарные операции.

Глава 1. Основные понятия теории графов

 

 

Несколько примеров дадут немного поверхностного представления о графе. Так типичным графом является схема метро или какой-либо другой маршрут. В частности, программисту знакома компьютерная сеть, также являющаяся графом. Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точки – это отдельные серверы, а линии – различные виды электрических сигналов. В метрополитене точки – станции, линии – туннели, проложенные между ними. В теории графов точки именуется вершинами, а линии – ребрами (дугами). Таким образом, граф – это совокупность вершин, соединённых ребрами.

Математика оперирует не содержанием вещей, а их структурой, абстрагируя ее из всего того, что дано как целое. Пользуясь именно этим приемом, мы можем заключать о каких-либо объектах как о графах. А поскольку теория графов — это часть математики, то для нее нет абсолютно никакого значения, что в принципе представляет собой объект; важно лишь то, является ли он графом, т. е. обладает ли обязательными для графов свойствами. Поэтому, прежде чем привести примеры, мы выделяем в рассматриваемом объекте лишь то, что как нам кажется, позволит показать аналогию, отыскиваем общее.

Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. В качестве примера показана полносвязная топология (Рисунок 1).

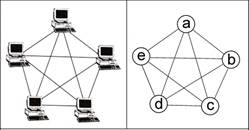
Рисунок 1 – Полносвязная топология предоставленная в виде графа

 

Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Стоит отметить, что в данном примере не используется ни одной петли, то есть такого ребра, которое выходит из вершины и сразу же входит в нее, но петли могут встречаться в задачах.

Вот некоторые важные обозначения, используемые в теории графов:

·                     G= (V, E), здесь G – граф, V – его вершины, а E – ребра;

·                     |V| – порядок (число вершин);

·                     |E| – размер графа (число рёбер).

В нашем случае (рисунок 1) |V|=5, |E|=10;

Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (Рисунок 1). Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом (Рисунок 2).

В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.

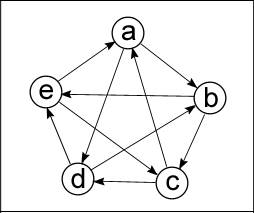
Рисунок 2 – Ориентированный граф

 

В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда, когда ребро выходит из h и входит в s, но не наоборот.

Ориентированные графы имеют следующую форму записи:

G= (V, A), где V – вершины, A – направленные ребра.

Третий тип графов – смешанные графы (Рисунок 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G= (V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.

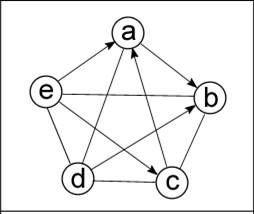
Рисунок 3 - Ориентированный граф

 

В графе на рисунке 3 одни дуги, направленные [(e, a), (e, c), (a, b), (c, a), (d, b)], другие – ненаправленные [(e, d), (e, b), (d, c), (a, d), (b, c)].

Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает вследствие различного их изображения. Но это не всегда так. Возьмем два графа (Рисунок 4, Рисунок 5).

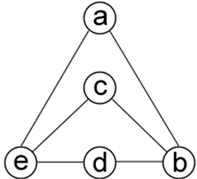
Рисунок 4 – граф (a)

 

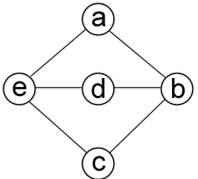
Рисунок 5 – граф (b)

 

Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие графы называются изоморфными, т. е. обладающими тем свойством, что какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На рисунке 4 и рисунке 5 изображены два изоморфных графа.

Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра, тогда такой граф взвешенный. В разных задачах в качестве веса могут выступать различные виды измерений, например, длины, цены маршруты и т. п. В графическом представлении графа весовые значения указываются, как правило, рядом с ребрами.

В любом из рассмотренных нами графов имеется возможность выделить путь и, причем не один. Путь – это последовательность вершин, каждая из которых соединена с последующей посредством ребра. Если первая и последняя вершины совпадают, то такой путь называется циклом. Длина пути определяется количеством составляющих его ребер. Например, на рисунке 4 путем служит последовательность [(e), (a), (b), (c)]. Этот путь является подграфом, так как к нему применимо определение последнего, а именно: граф G’= (V’, E’) является подграфом графа G= (V, E), только тогда, когда V’ и E’ принадлежат V, E.

 

 

Глава 2. Способы предоставления графов

 

 

Граф, как и большинство других математических объектов, может быть представлен с помощью перечисления множеств, с помощью графического изображения, так же может изображаться матричным способом.

Способ перечисления множеств – это способ перечисления множеств V и E составляющих множество G:

·                     G= (V, E), здесь G – граф, V – его вершины, а E – ребра;

·                     |V| – порядок (число вершин);

·                     |E| – размер графа (число рёбер).

Графический способ – способ графического отображения взаимодействий между множествами V и E в графе G.

Матричный способ разберём конкретней, потому что с помощью матриц выполняются операции над графами, которых они описывают.

Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов задает размер матрицы.

Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1. Прежде чем отобразить граф через матрицу смежности, рассмотрим простой пример такой матрицы (Рисунок 6).

Это двоичная квадратная матрица, т. к. число строк в ней равно числу столбцов, и любой из ее элементов имеет значение либо 1, либо 0. Первая строка и первый столбец (не входят в состав матрицы, а показаны здесь для легкости ее восприятия) содержат номера, на пересечении которых находится каждый из элементов, и они определяют индексное значение последних. Имея в наличии лишь матрицу такого типа, несложно построить соответствующий ей граф, обратим внимание на рисунок 7.

 

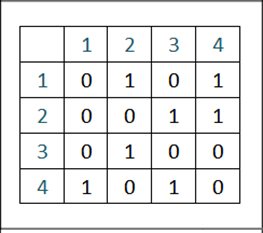
Рисунок 6 – Матрица смежности

 

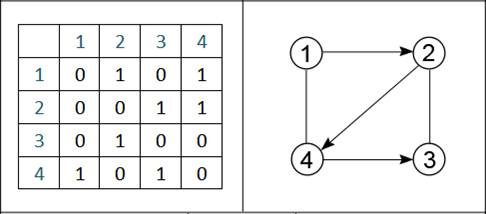
Рисунок 7 – Матрица смежности и соответствующий граф

 

Слева на рисунке изображена все та же матрица смежности, имеющая размерность 4×4. Числа, выделенные синим, можно рассматривать как вершины смешанного графа, расположенного справа – того, представлением которого является матрица.

Для графа со взвешенными ребрами ячейки матрицы смежности принимают значения веса ребра.

Матрица инцидентности. Говорить о том, что ребро g и каждая из вершин u и y инцидентна g, стоит лишь в том случае, если g соединяет u и y. Уяснив это, перейдем к рассмотрению данного метода. Матрица инцидентности строиться по похожему, но не по тому же принципу, что и матрица смежности. Так если последняя имеет размер n×n, где n – число вершин, то матрица инцидентности – n×m, здесь n – число вершин графа, m – число ребер. То есть теперь чтобы задать значение какой-либо ячейки, нужно сопоставить не вершину с вершиной, а вершину с ребром.

В каждой ячейки матрицы инцидентности неориентированного графа стоит 0 или 1, а в случае ориентированного графа, вносятся 1, 0 или -1. То же самое, но наиболее структурировано:

1) Неориентированный граф

a. 1 – вершина инцидентна ребру

b. 0 – вершина не инцидентна ребру

2) Ориентированный граф

a. 1 – вершина инцидентна ребру, и является его началом

b. 0 – вершина не инцидентна ребру

c. -1 – вершина инцидентна ребру, и является его концом

Построим матрицу инцидентности сначала для неориентированного графа, а затем для орграфа. (смотреть Рисунок 8)

 

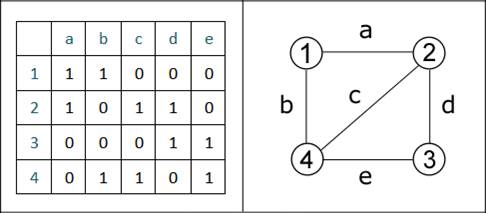
Рисунок 8 – Матрица инцидентности и соответствующий ей неориентированный граф

Ребра обозначены буквами от a до e, вершины – цифрами. Все ребра графа не направленны, поэтому матрица инцидентности заполнена положительными значениями. (Рисунок 9)

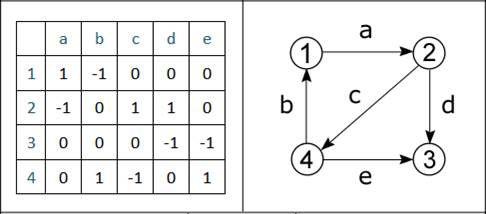
Рисунок 9 - Матрица инцидентности и соответствующий ей ориентированный граф

 

Для орграфа графа матрица имеет немного другой вид. В каждую из ее ячеек внесено одно из трех значений. Обратите внимание, что нули в матрицах, изображенных на рисунке 8 и рисунке 9, занимают одинаковые позиции, ведь в обоих случаях структура графа одна. Но некоторые положительные единицы сменились на отрицательные, например, в неориентированном графе ячейка (1, b) содержит 1, а в орграфе -1. Действительно, это уместно, т. к. в первом случае ребро b не направленное, а во втором – направленное, и, причем вершиной входа для него является вершина «1».

Каждый столбец отвечает за какое-либо одно ребро, поэтому граф, описанный при помощи матрицы инцидентности, всегда будет иметь следующий признак: любой из столбцов матрицы инцидентности содержит две единицы, либо 1 и -1 когда это ориентированное ребро, все остальное в нем – нули.

Для графа со взвешенными ребрами ячейки матрицы инцидентности принимают значения веса ребра, при то что в орграфе значение ячейки может быть отрицательным.

 

Глава 3. Операции над графами

 

 

3.1. Операции над графами

 

Операции над графами образуют новые графы из старых. Операции можно разделить на следующие основные категории.

1.                 Унарные операции — это метод создания нового графа из старого.

a.                  Элементарные унарные операции. Иногда этот класс операций называют «операции редактирования» графов. Они создают новый граф из исходного графа путём простых, локальных изменений, таких как добавление или удаление вершины, или дуги, слияние или расщепление вершин, стягивание графа, и т.д.

b.                 Сложные унарные операции. Это такие операции как: рёберный граф, двойственный граф, дополнение графа, минор графа, возведение в степень, граф Мычельского.

2.                 Бинарные операции - создаёт новый граф из двух исходных графов G1(V1, E1) и G2(V2, E2):

Существуют такие бинарные операции как несвязанное объединение графов или просто объединение, соединением двух графов, произведение графов, прямое произведение графов, лексикографическое произведение графов, строгое произведение графов, тензорное произведение графов, зигзаг-произведение.

Все операции, которые нужно произвести, производятся с помощью матриц смежности, верней путём видоизменения исходной матрицы исходного графа.

 

3.2. Бинарные операции

 

Объединение графов G₁ и G₂, обозначаемое как G₁ v G₂, представляет такой граф G₃ = (X₁ v X₂, A₁ V A₂), что множество его вершин является объединением Х₁ и Х₂, а множество ребер – объединением A₁ и A₂. Граф G₃, полученный операцией объединения графов G₁ и G₂, показан на рисунке 10 (д), а его матрица смежности – на рисунок 10 (е). Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G₁ и G₂.

 

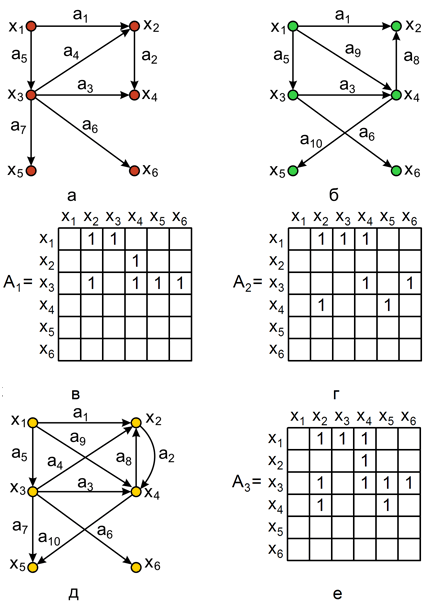
Рисунок 10 – Операция объединения графов

Пересечение графов G₁ и G₂, обозначаемое как G₁^G₂, представляет собой граф G₄ = (X₁ ^ X₂, A₁ ^ A₂). Таким образом, множество вершин графа G₄ состоит из вершин, присутствующих одновременно в G₁ и G₂. Операция пересечения графов G₁ ^ G₂ показана на рисунке 11 (в), а результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов G₁ и G₂. показана на рисунке 11 (г).

 

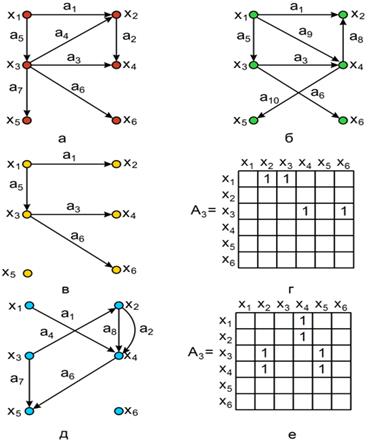
Рисунок 11 – Операция пересечения графов

 

Операция пересечения и кольцевой суммы: (а) – граф G₁; (б) – граф G₂ ; (в) – граф G₁^G₂; (г) – матрица смежности графа G₁^G₂; (д) – граф G₁G₂; (е) – матрица смежности графа G₁G₂

Кольцевая сумма двух графов G₁ и G₂, обозначаемая как G₁G₂, представляет собой граф G₅, порожденный на множестве ребер A₁A₂. Другими словами, граф G₅ не имеет изолированных вершин и состоит только из ребер, присутствующих либо в G₁ , либо в G₂ , но не в обоих одновременно. Кольцевая сумма графов G₁ u G₂ показана на рисунок 11(д), а результирующая матрица смежности получается операцией поэлементного логического сложения по mod 2 матриц смежности исходных графов G₁ u G₂, показана на рисунок 11(е).

Легко убедиться в том, что три рассмотренные операции коммутативны т.е. G₁ ^ G₂ = G₂ ^ G₁ ;  G₁ u G₂ = G₂ u G₁ ; G₁G₂ = G₂G₁, и многоместны, т.е. G₁ u G₂ u G₃ u G₄ u … , G₁ ^ G₂ ^ G₃ ^ G₄ ^ … и так далее.

 

3.3. Унарные операции

 

Удаление вершины. Если х_i -вершина графа G = (X, A), то G–х_i -порожденный подграф графа G на множестве вершин X–х_i, т. е. G–х_i является графом, получившимся после удаления из графа G вершины х_iи всех ребер, инцидентных этой вершине. Удаление вершины х₃ показано на рисунок 12 (б) (для исходного графа, изображенного на рисунке 12(а)). Матрица смежности исходного графа представлена на рисунке 13(а). Результирующая матрица смежности графа после выполнения операции удаления вершины х_i получается путем удаления, соответствующего i -того столбца и i -той строки из исходной матрицы и "сжимания" матрицы по вертикали и горизонтали начиная с (i+1) -того столбца и (i+1) -той строки (Рисунок 13(б)). В дальнейшем элементы графа могут быть пере обозначены.

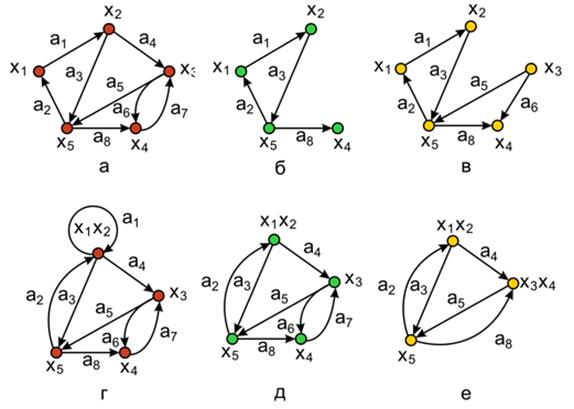
Рисунок 12 – Графы, предоставленные графическим способом

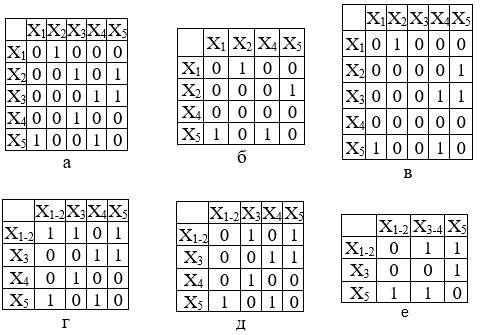
Рисунок 13 – Графы, предоставленные матричным способом

 

Удаление ребра или удаление дуги. Если a_i - дуга графа G = (X, A), то G-a_i – подграф графа G, получающийся после удаления из G дуги a_i. Заметим, что концевые вершины дуги a_i не удаляются. Удаление из графа множества вершин или дуг определяется как последовательное удаление определенных вершин или дуг. Удаление дуг a₄ и a₇ показано на рисунке 12, в. Результирующая матрица смежности графа после выполнения операции удаления дуги a_i получается путем удаления соответствующих элементов из исходной матрицы (Рисунок 13 (в)).

Замыкание или отождествление. Говорят, что пара вершин х_i и x_j в графе G замыкается (или отождествляется), если они заменяются такой новой вершиной, что все дуги в графе G, инцидентные х_i и x_j, становятся инцидентными новой вершине. Например, результат замыкания вершины х₁ и х₂ показан на рисунке 12(г) для графа G (рисунок 12(а)). Матрица смежности графа после выполнения операции замыкания вершин х_i и x_j получается путем поэлементного логического сложения i - го и j - го столбцов и i -ой и j - строк в исходной матрице и "сжимания" матрицы по вертикали и горизонтали (Рисунок 13(г)).

Стягивание. Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин. Граф, изображенный на рисунок 12(д) получен стягиванием дуги a₁, а на рисунок 12(е) – стягиванием дуг a₁, a₆ и a₇. Соответствующие результирующие матрицы смежности показаны в рисунке 13(д) и рисунке 13(е).

 

ЗАКЛЮЧЕНИЕ

 

 

Графы - это замечательные математические объекты, с помощью которых можно решать математические, экономические и логические задачи, различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Многие математические факты удобно формулировать на языке графов. Теория графов является частью многих наук. Теория графов — одна из самых красивых и наглядных математических теорий. В последнее время теория графов находит всё больше применений и в прикладных вопросах.

 В качестве моделей графы удобно использовать в тех случаях, когда рассматриваются системы каких-либо объектов, между которыми существуют определенные связи, а также в тех случаях, когда изучается структура системы, возможности ее функционирования. В информатике графы используются в операционных системах, алгоритмизации, структурных данных, моделирование и др.

Теория графов в настоящее время является интенсивно развивающимся разделом дискретной математики. Графы и связанные с ним методы исследований органически пронизывают на разных уровнях едва ли не всю современную математику. Язык графов прост, понятен и нагляден. Графовые задачи обладают рядом достоинств, позволяющих использовать их для развития соображения, улучшения логического мышления, применения смекалки. Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач.

Типичными графами являются схемы авиалиний, которые часто вывешивается в аэропортах, схемы метро, а на географических картах – изображение железных дорог.

 

Список используемых источников.

 

 

Клауди Альсин. Карты метро и нейронные сети. Теория графов. / Пер. с исп. — М.: Де Агостини, 2014. — 144 с.

Теория графов. Основные понятия и виды графов. [Электронный ресурс]. Режим доступа: http://kvodo.ru. –  заглавие с экрана - (Дата обращения: 03.05.19.)

Граф в математике. [Свободная электронная энциклопедия]. – Режим доступа: https://ru.wikipedia.org. – заглавие с экрана – (Дата обращения: 03.05.19)

Граф. [электронный ресурс] – режим доступа: https://prog-cpp.ru – заглавие с экрана – (Дата обращения: 03.05.19)

Теория графов. [электронный источник] – режим доступа: https://studfiles.net – заглавие с экрана – (Дата обращения: 03.05.19)

Графы – Математика [электронный учебник] – режим доступа: https://foxford.ru – заглавие с экрана – (Дата обращения: 03.05.19)

Операции над графами [электронный ресурс] – режим доступа: https://helpiks.org – заглавие с экрана – (Дата обращения: 03.05.19)

Лекция: операции над графами [электронный сборник лекций] – режим доступа: http://www.intuit.ru – заглавие с экрана   – (Дата обращения: 03.05.19)

Теоретико-множественные операции над графами. [электронный ресурс] – режим доступа: http://neerc.ifmo.ru - заглавие с экрана – (Дата обращения: 03.05.19)

Применение графов в различных областях жизни людей. [Электронный ресурс] – режим доступа: http://obuchonok.ru – заглавие с экрана – (Дата обращения: 03.05.19)

 

Скачано с www.znanio.ru