Лабораторная работа № 10. Изучение гибридных систем и разработка гибридных нейронечетких моделей средствами инструментария нечеткой логики

Лабораторная работа № 10. Изучение гибридных систем и разработка гибридных нейронечетких моделей средствами инструментария нечеткой логики

Цель работы

Изучить структуру и функции гибридной адаптивной системы нейронечеткого вывода ANFIS, научиться разрабатывать простейшие модели гибридных нейронечетких систем в среде MATLAB.

Общие теоретические положения

Гибридная нейронечеткая сеть представляет собой многослойную нейронную сеть специальной структуры, предназначенную для обработки числовой информации. Обработка информации в нейронечеткой сети осуществляется в соответствии с логикой работы нечеткой системы, а настройка параметров – по правилам обучения нейронных сетей. Тем самым в нейронечеткой сети реализована основная идея гибридизации – объединения преимуществ НС по наглядности представления и простоте содержательной интерпретации структуры правил вывода и нейронных сетей – по возможностям построения и обучения правил нечетких продукций.

Наибольшее распространение на практике получили гибридные сети, реализованные в форме так называемых адаптивных систем нейронечеткого вывода ANFIS (Adaptive Neuro-Fuzzy Inference System). ANFIS представляет собой нейронную сеть с несколькими входами, на которые подаются числовые значения входных переменных НС, и одним выходом, с которого снимаются числовые значения выходной переменной.

Отличием гибридных сетей ANFIS от нечетких систем типа Мамдани, реализующих традиционные схемы нечеткого вывода, является то, что заключениями нечетких правил сети ANFIS являются не лингвистические значения нечетких переменных, а обычные вещественные числа. Так, простейшая сеть ANFIS с двумя входными и одной выходной переменной работает с нечеткими правилами вида:

if x is A and  у is В  then   z= k,                             (4.5)

где  А и В – нечеткие множества антецедента; к – четко заданная константа консеквента.

Более сложные сети ANFIS работают с нечеткими правилами, заключениями которых являются линейные зависимости от входных переменных. Такие правила имеют вид выражений:

If x as A and у is В then z= p • х + q • у + k,                   (4.6)

где р, q и k – числовые константы.

Гибридная сеть на основе нечетких правил вида (4.5) называется ANFIS-системой 0-го порядка. Гибридная сеть на основе нечетких правил вида (4.6) называется ANFIS-системой 1-го порядка.

Для простейшей ANFIS-системы 0-го порядка, состоящей из n правил вида (4.5), значение z, полученное на выходе НС при подаче на ее входы значений x и у, определяется в соответствии с формулой:

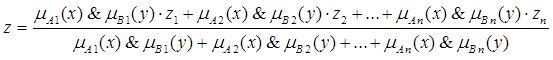,     (4.7)

где  – нечеткие термы, описывающие предусловие i-го правила;  – числовая константа консеквента i-го правила;  – ФП нечетких термов       и, n – число правил.

Описание графического инструментария разработки гибридных  нейронечетких систем в среде MATLAB

В пакете Fuzzy Logic Toolbox системы MATLAB гибридные сети реализованы в форме адаптивных ANFIS-систем нейронечеткого вывода. Разработка и исследование гибридных сетей оказывается возможной как в интерактивном режиме с помощью специального графического редактора адаптивных сетей, получившего название ANFIS-редактора, так и в режиме командной строки с помощью ввода имен соответствующих функций с необходимыми аргументами непосредственно в окно команд системы MATLAB.

ANFIS-редактор позволяет создавать или загружать конкретную модель адап­тивной системы нейронечеткого вывода, выполнять ее обучение, визуализировать ее структуру, изменять и настраивать ее параметры, а также использовать настроенную сеть для получения результатов нечеткого вывода.

Графический интерфейс ANFIS-редактора вызывается функцией anfisedit из командной строки (рис. 10).

Главное меню ANFIS-редактора достаточно простое и предназначено для работы с предварительно созданной системой нечеткого вывода. Основную часть графического интерфейса занимает окно визуализации данных, которое расположено ниже главного меню. Для вновь создаваемой гибридной сети это окно не содержит никаких данных.

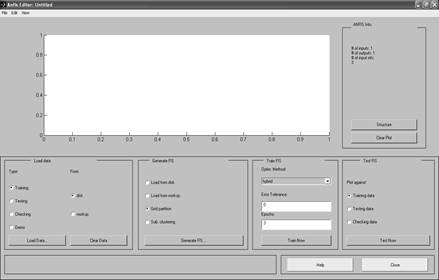
Рис. 10. Графический интерфейс ANFIS-редактора

Для создания структуры гибридной сети необходимо загрузить данные путем нажатия кнопки Load Data в левой нижней части графического интерфейса. При этом данные могут быть загружены из внешнего файла (disk) или из рабочей области (Workspace). В первом случае необходимо предварительно создать файл с исходными данными (файл с расширением .dat), который представляет собой обычный текстовый файл.

Исходные данные представляют собой обычную числовую матрицу размерности  , в которой количество строк т соответствует объему выборки, первые n столбцов – значениям вход­ных переменных модели, а последний столбец – значению выходной перемен­ной. Согласно правилам системы MATLAB отдельные значения матрицы отде­ляются пробелами, а каждая строка матрицы завершается символом «перевод каретки» (клавиша <Enter>).

Загружаемые исходные данные могут быть одного из следующих типов: обучающие данные (Training) – обязательные данные, которые используются для построения гибридной сети; тестовые данные (Testing) – необязательные данные, которые используются для тестирования построенной гибридной сети; проверочные данные (Checking) – необязательные данные, которые исполь­зуются для проверки построенной гибридной сети на предмет ее переобучения.

Генерация структу­ры гибридной сети осуществляется путем нажатия кноп­ки Generate FIS в нижней части рабочего окна ANFIS-редактора. При этом две первые опции относятся к предварительно созданной структуре гибридной сети (Load from disk – загрузка с диска, Load from worksp. – загрузка с рабочей памяти), а две последних – к форме разбиения входных переменных модели (Grid partition – независимое разбиение входных переменных на области их значений, Sub. Clustering – процедура субтрактивной кластеризации для предварительного разбиения значений входных переменных на кластеры близких значений. Здесь же в диалоговом окне ANFIS-редактора осуществляется выбор ФП для отдельных термов входных и выходной переменной.

Визуализация структуры гибридной сети осуществляется путем нажатия кнопки Structure в правой части графического окна. Структура полученной       в результате системы нечеткого вывода FIS отображается в отдельном окне   (рис. 4.12).

Обучение гибридной сети инициализируется кнопкой Train Now, расположенной в нижней части окна ANFIS-редактора. При этом ход процесса обучения иллюстрируется в окне визуализации в форме графика зависимости ошибки от количества циклов обучения.

Этапы разработки нечеткой системы в интерактивном режиме

Процесс создания гибридной НС сводится к следующим этапам.

Этап 1. Подготовка обучающих данных. Обучающие данные подготавливаются с помощью редактора-отладчика m-файлов в виде числовой матрицы размерности  , в которой количество строк т соответствует объему обучающей выборки, первые n столбцов – значениям n вход­ных переменных.

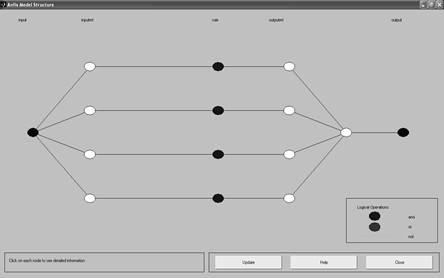
Рис. 11. Пример структуры гибридной сети из 4-х правил

Этап 2. Загрузка файла с  обучающими  данными   в ANFIS-редактор. Эта процедура начинается с вызова ANFIS-редактора путем выполнения команды anfisedit в командной строке  системы MATLAB. После чего осуществляется загрузка обучающих данных в ANFIS-редактор путем нажатия кнопки Load data.  В графическом окне ANFIS-редактора появляется окно ме­неджера файлов, позволяющее выбрать имя файла данных, имеющее текстовый формат и расширение dat. Если загрузка данных прошла успешно, то в рабочем окне редактора появляются обучающие данные, отмеченные кружками на координатной плоскости «Значение выходной переменной – Порядковый номер данного».

Этап 3. Генерация структуры нечеткой системы. Генерация структуры осуществляется автоматически после загрузки данных путем нажатия клавиши Generate FIS. После генерации структуры нечеткой системы в окне ввода Number of MFs задается количество нечетких термов для каждого входа, в окне MFType – тип ФП входных переменных, а в окне OUTPUT – тип ФП выходной переменной. Структуру сгенерированной системы можно просмотреть с помощью клавиши Structure.

Этап 4. Обучение нейронечеткой сети. После того как определено количество входных и выходных перемен­ных и сформирована структура гибридной системы, осуществляется процесс ее обучения. Для этого в меню Train FIS выбирается алгоритм обучения (Hybrid или Васкргор), устанавливаются целевое значение ошибки Error Tolerance и количество циклов обучения Epochs. Нажатие клавиши Train Now запускает процесс обучения.

Этап 5. Отладка нейронечеткой сети. Отладка гибридной сети начинается с проверки результатов обучения нажатием клавиши Test Now. Для выполнения тестирования необхо­димо загрузить тестовые данные в режиме Testing data в окне менеджера файлов. Результат аппроксимации тестовых дан­ных отображается в окне ANFIS-редактора.

Дальнейшая настройка параметров построенной и обученной гибридной сети может быть выполнена с помощью рассмотренных ранее стандартных графиче­ских средств пакета Fuzzy Logic Toolbox. Для этого рекомендуется сохранить созданную систему нечеткого вывода во внешнем файле с расширени­ем fis, после чего следует загрузить этот файл в FIS-редактор. При этом также становятся доступными редактор функций принадлежности сис­темы нечеткого вывода (MF-редактор), редактор правил (Rule Editor), программа просмотра правил (Rule Viewer) и программа просмотра поверхности системы нечеткого вывода (Surface Viewer).

Этап 6. Исследование модели гибридной сети. Для исследования построенной модели гибридной сети можно воспользоваться программой просмотра правил (Rule Viewer). Для получения интересующего зна­чения выходной переменной необходимо задать конкретные значения входных переменных аналогично общим рекомендациям систем нечеткого вывода. При этом на графике функций принадлежности выходной переменной будет указано искомое значение выходной переменной. В дополнение к этому можно выполнить визуальный анализ поверхности вывода для построенной гибридной сети, которая также позволяет оценить значения выходной переменной. Выполнить анализ обученной и настроенной гибридной сети можно посредством визуализации поверхности нечеткого вывода. Для этой цели следует воспользоваться программой просмотра поверхности системы не­четкого вывода.

Пример разработки гибридной системы

Для иллюстрации процесса разработки гибридной сети в системе MATLAB рас­смотрим задачу построения адаптивной системы нейронечеткого вывода для аппроксимации функциональной зависимости , которая, например, может упрощенно описывать процесс разгона отцепа, скатывающегося с горки, на временном интервале Т = [0–2] с. Этот пример позволяет не только уточнить содержание и после­довательность этапов разработки, но и оценить точность полученной нечеткой модели посредством сравнения прогнозируемых модельных значений с известными заранее значениями соответствующей функции.

Общая последовательность процесса разработки модели гибридной сети приводится ниже.

1 Для начала с помощью редактора-отладчика m-файлов подготовим обучаю­щие данные, которые содержат шесть строк пар «Значение входной переменной t – Значение выходной переменной y» следующего вида (рис. 12).

 Сохраним обу­чающие данные во внешнем файле с именем function.dat.

2 Загружаем файл с обучающими данными в ANFIS-редактор (рис. 13). В рабочем окне редактора появляются обучающие данные, отмеченные кружками на координатной плоскости «Значение выходной переменной – Порядковый номер данного».

Рис. 12. Обучающие данные для примера разработки

гибридной сети ANFIS

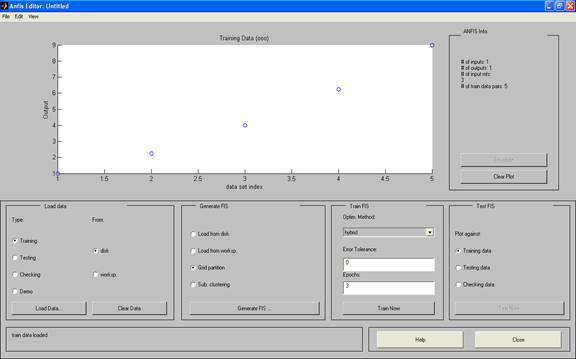
Рис. 13. Графический интерфейс ANFIS-редактора после загрузки

обучающих данных

3 Осуществляем генерацию структуры системы нечеткого вывода. В качестве параметров нечеткой системы принимаем те, которые по умолчанию устанавливаются ANFIS-редактором. Получим структуру FIS, изображенную на рисунке 14.

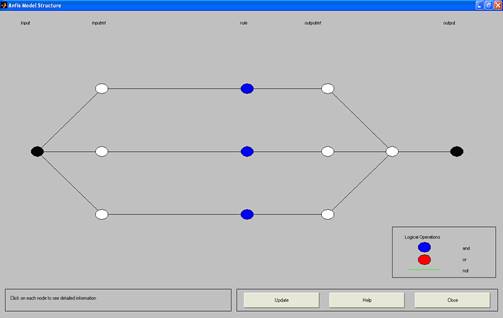
Рис. 14. Структура гибридной сети

4 Производим обучение сгенерированной системы нечеткого вывода. В качестве метода обучения выберем гибридный метод, уровень ошибки установим равным 0, а количество циклов обучения примем равным 40.

После обучения сети в рабочем окне ANFIS-редактора будет изображен график изменения ошибки в ходе выполнения отдельных циклов обучения  (рис. 15).

5 Выполним анализ точности построенной нечеткой модели гибридной сети с помощью программы просмотра поверхности соответствующей системы нечеткого вывода (рис. 16).

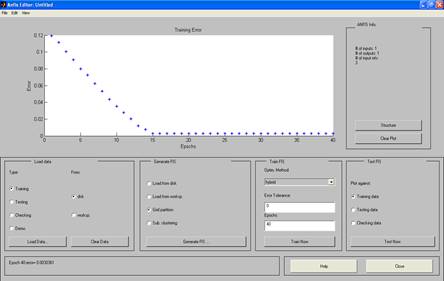
Рис. 15. График зависимости ошибки обучения

от количества циклов обучения

Рис. 16. Графический интерфейс просмотра поверхности

сгенерированной системы нечеткого вывода

Визуальное сравнение графика функции, полученной на выходе нечеткой системы, с точным графиком функции , которую должна воспроизводить эта система, позволяет сделать вывод о том, что, во-первых, имеется совпадение значений полученной функции и воспроизводимой функции во всех контрольных точках, а, во-вторых, характер полученной кривой, в целом соответствует моделируемой зависимости . Это свидетельствует об адекватности построенной нечеткой модели гибридной сети.

Дополнительная настройка модели может быть выполнена другими способами, наиболее приемлемыми из которых являются:

·                   использование обучающих выборок большего объема;

·                   использование дополнительного файла с проверочными данными, отсутствующими в исходной обучающей выборке.

Редактирование типов и параметров ФП нечетких термов входных  и выходной переменных с помощью MF-редактора системы MATLAB.

В заключение следует отметить, что даже простейший рассмотренный пример отражает творческий характер процесса построения и анализа моделей гибрид­ных сетей. При этом выбор того или иного способа настройки параметров нечеткой системы  зависит от специфики решаемой задачи, от объема обучающей выборки и характера проверочных данных. В случае недостаточной информации обучающих данных использование гибридных сетей может оказаться вообще нецелесообразным, поскольку получить адекватную нечеткую модель, а значит, и точный прогноз значений выходной переменной не представляется возможным. Именно по этим причинам необходим предварительный анализ всех возможно­стей применяемых нечетких моделей для решения конкретных задач в той или иной проблемной области. Подобный анализ необходимо выполнять с систем­ной точки зрения и с учетом всех складывающихся на данный момент обстоя­тельств. Только всесторонняя и полная оценка проблемной ситуации позволит разработать адекватную модель решения той или иной конкретной задачи не­четкого управления или принятия решений.

Задание

Лабораторная работа включает три задания, связанные с разработкой гибридных адаптивных систем в программной среде MATLAB.

Задание 1. Требуется разработать гибридную систему ANFIS в программной среде MATLAB, осуществляющую аппроксимацию функциональной зависимости  на интервале изменения входной переменной .

Объем обучающей выборки составляет пятнадцать значений пар «Вход-Выход», равномерно распределенных на интервале изменения входной переменной. В качестве нечетких термов для  входной переменной x использовать   5 термов: «Около нуля», «Малое отрицательное», «Отрицательное», «Малое положительное», «Положительное». Количество нечетких правил базы знаний гибридной модели равно 5.

Задание 2. Требуется разработать гибридную систему ANFIS в программной среде MATLAB, моделирующую динамическую систему, которая задана следующим разностным уравнением:

,

где  – текущее значение выхода динамической системы;  – предыдущие значения выхода динамической системы в моменты времени (t - 1) и (t - 2) соответственно.

Выход нечеткой системы изменяется в интервале значений , шаг моделирования  с, объем обучающей выборки – 15 первых отсчетов, вычисленных по разностному уравнению. Для входных переменных  использовать по три нечетких терма, заданных на единичном интервале [0; 1].

Задание 3. Требуется разработать гибридную систему ANFIS в программной среде MATLAB, реализующую процесс нелинейной авторегрессии временного ряда на основе простейшей одношаговой модели .

Обучающая выборка включает семь первых отсчетов временного ряда, приведенного ниже в таблице, а проверочная выборка – восемь последних значений этого же ряда.

Таблица