Лабораторная работа № 2. Работа с матрицами

            Цель работы

         Изучить основные матричные операции в среде MATLAB.

         Основные теоретические положения

         Все данные MATLAB представляет в виде массивов. Очень важно правильно понять, как использовать массивы. Без этого невозможна эффективная работа в MATLAB, в частности: построение графиков, решение задач линейной алгебры, статистики, обработки данных и многих других.

Напомним, что такое массив. Массив – упорядоченная, пронумерованная совокупность однородных данных. У массива должно быть имя. Массивы различаются по числу размерностей или измерений: одномерные, двумерные, многомерные. Размером массива называют число элементов вдоль каждого из измерений. Доступ к элементам осуществляется при помощи индекса. В MATLAB нумерация элементов массивов начинается с единицы. Это значит, что индексы должны быть больше или равны единице.

Важно понять, что вектор, вектор-строка, матрица или тензор являются математическими объектами, а одномерные, двумерные или многомерные массивы – способы хранения этих объектов в компьютере. Всюду дальше будут использоваться слова вектор и матрица, если больший интерес представляет сам объект, чем способ его хранения. Вектор может быть записан в столбик (вектор-столбец) и в строку (вектор-строка). Вектор-столбцы и вектор-строки часто будут называться просто векторами, различие будет сделано в случаях, когда важен способ хранения вектора в MATLAB.

         Порядок выполнения работы

Пример 1. Ввод матриц, простейшие операции

Вводить небольшие по размеру матрицы удобно прямо из командной строки. Введите матрицу размерностью два на три:

.

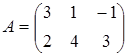Для хранения матрицы используйте двумерный массив с именем A. При вводе учтите, что матрицу А можно рассматривать как вектор-столбец из двух элементов, каждый из которых является вектор-строкой длиной три, следовательно, строки при наборе отделяются точкой с запятой:

>> A = [3 1 -1; 2 4 3]

A =

     3     1    -1

     2     4     3

>> 

Для изучения простейших операций над матрицами нам понадобится еще несколько матриц. Рассмотрим другие способы ввода. Введите квадратную матрицу размера три так, как описано ниже:

.

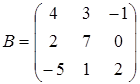Начните набирать в командной строке

>> B = [4 3 -1

        2 7 0

        -5 1 2]

Нажмите клавишу <Enter>. Обратите внимание, что MATLAB ничего не вычислила. Курсор мигает на следующей строке без символа >>. Продолжи­те ввод матрицы построчно, нажимая в конце каждой строки <Enter>. По­следнюю строку завершите закрывающей квадратной скобкой, получается:

B =

     4     3    -1

     2     7     0

    -5     1     2

>> 

Еще один способ ввода матриц состоит в том, что матрицу можно тракто­вать как вектор-строку, каждый элемент которой является вектор-столбцом. Например, матрицу два на три

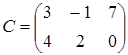
можно ввести при помощи команды:

>> C= [[3; 4] [-1; 2] [7; 0]]

C =

     3    -1     7

     4     2     0

>> 

Итак, в рабочей среде содержится три матрицы, две прямоугольные и одна квадратная.

Пример 2. Обращение к элементам матриц

Доступ к элементам матриц осуществляется при помощи двух индексов – номеров строки и столбца, заключенных в круглые скобки, например:

>> C(2, 3)

ans =

     0

>> 

Элементы матриц могут входить в состав выражений:

>> C(1, 1) + C(2, 2) + C(2, 3)

ans =

     5

>> 

В качестве индексов могут выступать векторы, содержащие номера нужных строк и столбцов. Например, для выделения элементов первой и второй строк второго и третьего столбцов введенной выше матрицы В достаточно ввести команды:

>> i = [1 2];

>> j = [2 3];

>> B1 = B(i, j)

B1 =

     3    -1

     7     0

>> 

Для доступа к элементам матрицы можно использовать один индекс, задающий порядковый номер элемента матрицы в векторе. Напри­мер, элементы матрицы С, определенной в предыдущем примере, записаны в таком порядке:

C(1, 1), C(2, 1), C(1, 2),  C(2, 2), C(1, 3), C(2, 3)

Поэтому обращение к элементам матрицы как к элементам вектора при по­мощи одного индекса (индексация при помощи порядкового номера) при­водит к такому результату:

>> C(5)

ans =

     7

>> 

При этом следует помнить что, если один индекс случайно указан вместо двух – никакого предупреждения не выводится.

Пример 3. Сложение, вычитание, умножение, транспонирование и возведение в степень

При использовании матричных операций следует помнить, что для сложе­ния или вычитания матрицы должны быть одного размера, а при перемно­жении число столбцов первой матрицы обязано равняться числу строк вто­рой матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус. Найдите сумму и раз­ность матриц С и А, определенных в примере 1:

>> S = A + C

S =

     6     0     6

     6     6     3

>> R = C - A

R =

     0    -2     8

     2    -2    -3

>> 

Для умножения матриц предназначена «звездочка»:

>> P = C * B

P =

   -25     9    11

    20    26    -4

>> 

Умножение матрицы на число тоже осуществляется при помощи «звездочки»:

>> P = A * 3

P =

     9     3    -3

     6    12     9

>> 

Транспонирование матрицы, так же как и вектора, производится при помощи  ' :

>> B'

ans =

     4     2    -5

     3     7     1

    -1     0     2

>> 

Возведение квадратной матрицы в целую степень производится с использо­ванием оператора ^ :

>> B2 = B^2

B2 =

    27    32    -6

    22    55    -2

   -28    -6     9

>> 

Убедитесь, что вы освоили простейшие операции с матрицами в MATLAB. Найдите значение следующего выражения

Учтите приоритет операций, сначала выполняется транспонирование, по­том возведение в степень, затем умножение, а сложение и вычитание произ­водятся в последнюю очередь.

>> (A + C)*B^3*(A - C)'

ans =

        1848        1914

       10290        3612

>> 

Контрольные вопросы

1       Что такое массив?

2       Какие способы ввода матриц Вы знаете?

3       Каким образом осуществляется доступ к элементам матрицы?

4       Каким критериям должны отвечать матрицы при сложении, вычитании и перемножении?

5       Какие символы предназначены для умножения, транспонирования и возведения в степень матриц?

Скачано с www.znanio.ru