
ЛАБОРАТОРНАЯ РАБОТА № 3
Разработка алгоритмов и программ циклической структуры
Цель: освоить методы разработки алгоритмов и программирования задач циклической структуры.
Краткие теоретические сведения
Часто при решении задач возникает необходимость многократно вычислять значения по одним и тем же математическим зависимостям для различных исходных данных. Многократно повторяющийся этап вычислений называется циклом, а вычислительный процесс, содержащий такие этапы, - циклическим.
Циклические алгоритмы находят самое широкое применение в программировании, так как при этом пользователь составляет программу, описывая в ней циклическую структуру один раз, а компьютер выполняет ее многократно.
Для организации циклических вычислений необходимо выполнить следующие действия:
- задать перед циклом начальное значение переменной, которая будет изменяться в рабочей области цикла;
- изменять переменную перед каждым новым повторением цикла;
- проверять условие окончания или повторения цикла, то есть переходить к началу цикла, если он не закончен, или выходить из цикла после его окончания.
Переменная, которая изменяется в цикле и от которой зависит условие выхода из цикла, называется параметром цикла.
В зависимости от способа организации циклических структур различают три типа циклов:
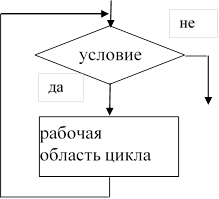
1) цикл с предусловием или цикл «ПОКА»
 |
28
Выполнение цикла начинается с проверки условия. Переход к выполнению рабочей области цикла осуществляется только в том случае, если условие выполняется, в противном случае происходит выход из цикла. В частном случае может оказаться, что рабочая область цикла не выполнится ни разу. Условие цикла необходимо подобрать так, чтобы действия, которые выполняются в рабочей области цикла, привели к нарушению его истинности, иначе произойдет зацикливание. Зацикливание – это бесконечное повторение выполняемых действий.
2) цикл с постусловием или цикл «ПОВТОРЯТЬ ... ДО»
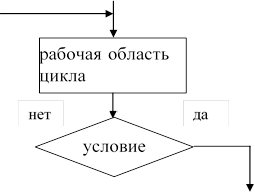 |
Выполнение цикла начинается с выполнения действий, таким образом, рабочая область цикла будет реализована хотя бы один раз. После этого происходит проверка условия. Если условие не выполняется, то происходит возврат к выполнению действий. Если условие истинно, то осуществляется выход из цикла. Для предотвращения зацикливания необходимо предусмотреть действия, приводящие к истинности условия.
3)
 |
Для организации цикла с известным числом повторений используется блок модификации.
29
В этом блоке указывается закон изменения переменной параметра цикла:
i - параметр цикла;
iн - начальное значение параметра; iк - конечное значение параметра;
∆i – шаг изменения параметра цикла.
Прочитать этот алгоритм можно следующим образом: «Изменяя параметр от начального значения до конечного значения, повторять рабочую область цикла».
Для организации циклических вычислительных процессов в программах используются операторы циклов REPEAT, WHILE и FOR.
Оператор цикла с постусловием REPEAT используется для организации цикла с неизвестным числом повторений и имеет вид:
Repeat
оператор 1;
оператор 2;
оператор 3;
……… оператор N
Until логическое выражение;
Оператор цикла выполняется следующим образом: сначала выполняется группа операторов цикла, затем вычисляется значение логического выражения. Если значение выражения имеет истинное значение, то цикл прекращается, иначе вновь выполняется группа операторов цикла.
Оператор цикла с предусловием WHILE используется также для организации цикла с неизвестным числом повторений и имеет вид:
While логическое выражение do оператор;
Оператор цикла выполняется следующим образом: вычисляется значение логического выражения, если значение логического выражения имеет истинное значение, то выполняется оператор, стоящий после ключевого слова do. Затем управление вновь передается на начало оператора While, снова вычисляется логическое выражение и процесс повторяется. Цикл прекращается если нарушается истинность логического выражения.
30
Если в цикле необходимо выполнить несколько операторов, то необходимо использовать составной оператор и оператор цикла While будет иметь следующий вид:
While логическое выражение do begin
оператор 1;
………… оператор n
end;
Оператор цикла FOR используется для организации цикла с известным числом повторений. Существует два вида записи оператора:
- при увеличении значения параметра цикла
For i:= n1 to n2 do оператор;
- при уменьшении значения параметра цикла
For i:= n2 downto n1 do оператор;
где
i - параметр цикла;
n1 - начальное значение параметра цикла; n2 - конечное значение параметра цикла.
Оператор цикла выполняется следующим образом: сначала вычисляется начальное и конечное значение параметра цикла, затем параметру цикла присваивается начальное значение и сравнивается с конечным значением. Пока параметр меньше или равен конечному значению (первый вариант) или более или равен конечному значению (второй вариант) выполняется оператор, иначе происходит выход из цикла. После выполнения оператора цикла параметру цикла присваивается следующее значение.
Если в цикле необходимо выполнить группу операторов, то необходимо использовать составной оператор и оператор цикла For будет иметь следующий вид:
For i := n1 to n2 do begin
оператор 1;
………… оператор n
end;
31
Пример 1. Вычислить значение переменной Y, используя формулы:
ìx + 4,
![]() y = íх 2
,
y = íх 2
,
если если
х ³ 5
x < 5
для
- 2 £ x £ 8
Dx = 1
Для вычисления значений переменной Y организовать цикл с предусловием.
Решение.
Исходные данные: хн, хк, ∆х. Результат вычислений: значения Y.
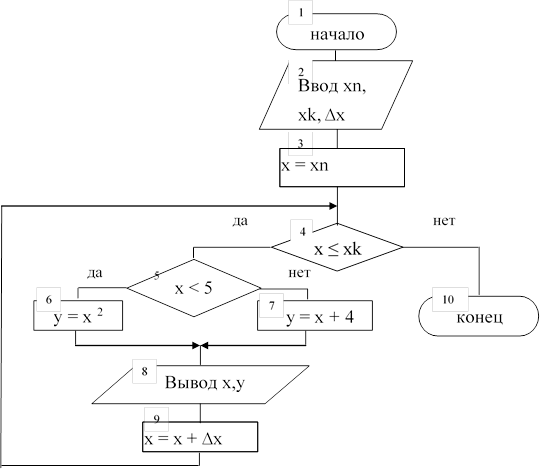 |
Текст программы решения задачи имеет вид: Program pr1;
Var xn,xk,dx,x,y:real; begin
writeln („Ввод xn,xk,dx‟); readln (xn,xk,dx); x := xn;
while x <= xk do begin
32
end.
end;
if x < 5 then y := sqr(x) else y := x + 4; writeln („x =‟, x : 6 : 2, „ y =‟, y : 6 : 2); x := x + dx
Пример 2. Вычислить значение переменной Х, используя формулы:
![]() x = 2,5a - c
x = 2,5a - c
a 2 - 2ac
для
- 3 £ a £ 3;
Da = 1,5
Для вычисления значений переменной Х организовать цикл с постусловием.
Решение.
Исходные данные: ан, ак, ∆а, с. Результат вычислений: значения Х.
Ограничения: для вычисления переменной Х необходимо дополнительно проверить условие а2-2ас¹0, иначе вывести текстовое сообщение «деление на ноль».
Схема алгоритма решения задачи имеет вид:
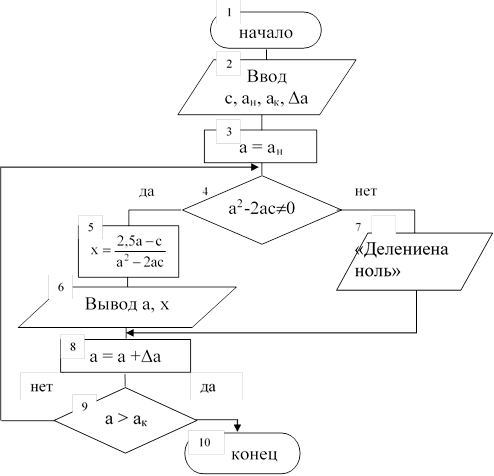 |
33
Текст программы решения задачи имеет вид:
Program pr2; Label 1;
Var аn,аk,dа,а,с,x:real; begin
writeln („Ввод an,ak,da,c‟);
readln (an,ak,da,c); a := an;
repeat
if sqr(a) – 2 * a * c <> 0 then
x := (2.5 * а - с) / (sqr(a) – 2 * a * c) else
begin
writeln („a =‟, a : 6 : 2, „ деление на ноль‟); goto 1
end.
end;
writeln („a =‟, a : 6 : 2, „ x =‟, x : 6 : 2); 1: a := a + da
until a > ak;
Пример 3. Вычислить значение переменной Y, используя формулы:
y = sin(ax)+ 2
1- x
для
- 5 £
x £ 5
Dx = 1
Определить
P = Õ y,
y>0
S = å y и
количество
у < 0.3
Для вычисления значений переменной Y организовать цикл с известным числом повторений.
Решение.
Исходные данные: хн, хк, ∆х, а.
Результат вычислений: значения Y, произведение положительных значений Y, сумма всех значений Y, количество значений Y, которые меньше 0,3.
Ограничения: для вычисления переменной Y необходимо дополнительно проверить условие 1-х¹0, иначе вывести текстовое сообщение «деление на ноль».
34
Схема алгоритма решения задачи имеет вид:
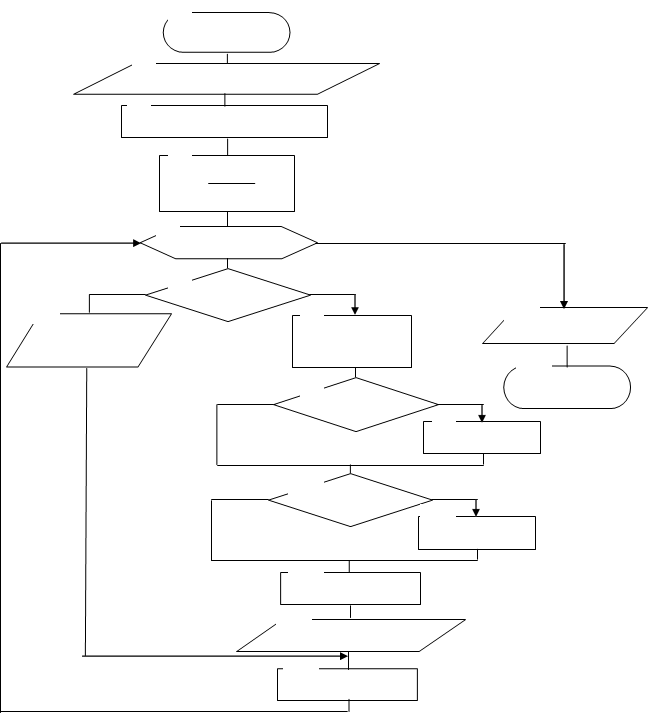 1
1
начало
2
Ввод а, хн, хк, ∆х
нет
14
«Деление
5
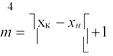 i = 1, m
i = 1, m
6 1-х ≠ 0
да
7
sin(ax)+ 2
16
k, P, S
на ноль»
нет
y = 1- x
8 y < 0.3
да
9
k = k + 1
17
конец
нет
10 y > 0
да
11
P = P · y
![]()
![]()
13
Вывод х, у
15
x = x + ∆x
Пояснения к решению задачи.
На схеме организации цикла с известным числом повторений отображается алгоритм, в котором параметром цикла является переменная i, изменяющаяся от 1 до m, где m - количество повторений цикла, вычисляемое по формуле:
ú Dх ê
35
Для вычисления количества, суммы и произведения используется принцип постепенного накопления. Формула, используемая для накопления суммы, имеет вид: Si = Si-1+y. При первом выполнении цикла вычисляется значение S1=S0+y, которое должно быть равно у. Поэтому начальному значению суммы перед циклом следует присвоить значение ноль.
Аналогично накапливается и произведение, с той лишь разницей, что для его накопления используется формула Pi = Pi-1 ∙ y, а начальное значение произведения должно быть равно единице.
Для накопления количества используется формула: ki = ki-1 +1. При первом выполнении цикла вычисляется значение k1 = k0 + 1, которое должно быть равно 1. Поэтому начальному значению количества перед циклом следует присвоить значение ноль.
В цикле происходит накопление произведения положительных значений Y и подсчет количества значений Y<0.3, а также накопление суммы всех значений Y. Вывод значений k, S, P осуществляется по окончании цикла, то есть значения необходимо вывести только один раз, когда они будут окончательно вычислены.
Текст программы решения задачи имеет вид: Program pr3;
label 1;
var xn,xk,dx,x,a,s,p,y : real; i,m,k : integer; begin
writeln („Ввод xn,xk,dx,a‟); readln (xn,xk,dx,a); k := 0; s := 0; p := 1; x := xn;
m := trunc ((xk-xn) / dx) + 1; for i := 1 to m do begin
if 1 – x < > 0 then y := (sin (a * x) + 2) / (1 - х) else
begin writeln („x =‟, x : 6 : 2, „ деление на 0‟); goto 1 end; if y < 0.3 then k := k + 1; if y > 0 then p := p * y;
s := s + y;
writeln („x =‟, x : 6 : 2, „ y =‟, y : 6 : 2); 1: x := x + dx;
end;
writeln („k =‟, k : 2, „ s =‟, s : 6 : 2, „ p =‟, p : 6 : 2); end.
36
Задание
1. Изучить лекционный материал и методические рекомендации для выполнения задания.
2. Разработать алгоритм для расчета заданных переменных: а) организовать цикл с постусловием;
б) организовать цикл с предусловием;
в) организовать цикл с известным числом повторений.
3. Составить программу на алгоритмическом языке Pascal.
4. Выполнить отладку и тестирование программы на компьютере.
5. Подготовить отчет о выполнении задания. Пример оформления отчета представлен в приложении 2.
6. Подготовить ответы на контрольные вопросы.
![]()
![]()
![]() Варианты заданий
Варианты заданий
|
№ п/п |
Вид задания |
|
1 |
а) Вычислить ì3 ax + 1 + b , если x < 5 z = ï Sin(bx + 2), если x = 5 y = z + b × cos z í ln(zx) ïb × cos(cx + 3), если x > 5 î Исходные данные: a, b, c; -2≤x≤4 ∆x=1
б) Вычислить ìeSinx, если a2 x < b3 у = ï b2 - a) / sin x, если a2x = b3 F = 5,37 y + ln(x3 + x2 + x) í( ïcos2 4x, если a2x > b3 î Считать F до тех пор, пока выражение под знаком логарифма больше 0. Определить Р = Õ F, S = å F F >0 F <0 Исходные данные: a, b; x≤3 ∆x=-0,1
в) Вычислить ì2sin2 x + x3, если x > 0 y = ï x a = ln y + 0,5y2 íï , если x £ 0 î x2 -1 Определить среднее арифметическое положительных значений y и произведение значений a. Исходные данные: -2≤x≤5 ∆x=0,1 |
![]()
![]()
![]()
![]() 37
37
|
2 |
а) Вычислить ì ïax 2 +1, если x < 3 ï z = íbx + cos2bx, если x = 3 y = sin(za) + cos(za) ï 1 ï , если x > 3 î ax - bx Исходные данные: a, b; -1≤x≤8 ∆x=0,5
б) Вычислить z = ïì (a + bc), если x ³ b y = 7,35z + 2a íï x - bc) / a, если x < b a2 + 1 î( Считать Y до тех пор, пока подкоренное выражение больше 1. Определить количество y<0, S = å y, P = Õ z y³0 Исходные данные: b, с, х; а≤3 ∆а=-0,2
в) Вычислить ì ï 2x 3 + 3 cos x, если x ³ 5 z = ï + ln( x + 6), если 1 £ x < 5 y = (x 2 + 2) × sin z í7 ï - 2 , если x < 1 î x 3 Определить количество zÎ[-1; 1] и сумму z Ï[-1; 1]. Исходные данные: -2≤x≤10 ∆x=1 |
|
3 |
а) Вычислить v = ïìy + x × 0,5 + sinx, если y £ a íï ×e xy+1 , если y > a î3 y = sinæ p x ö ç ÷ è 2 ø x = t 2 - 0.5 Исходные данные: a; 0≤t≤10 ∆t=2
б) Вычислить f = t 3 × ln z +1 P = 0,34 f + ln(t + b3 ) ì t 2 + £ z = ï2b a, если t 3 í ïî6t 3 + b, если t > 3 Считать Р до тех пор, пока выражение под знаком логарифма больше 0. Определить количество вычисленных Р, S = åP P>0 Исходные данные: a, t; b≤2 ∆b=-0,2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
38
|
|
в) Вычислить ì xy, если x 2 + y 2 < 1 ï x + y z = í x + , если x 2 + y 2 = 1 y = (a ï x - y îï2x + sin(x + y), если x 2 + y 2 > 1 Определить сумму значений z, количество отрицательных значений y. Исходные данные: a; -2≤x≤2 ∆x=0,5 |
+ x) 3
z>0 |
+ |
cos a 3
и произведение |
|
|
4 |
а) Вычислить ì1+ sinx, если x < 3 ï x a = í0.5cos 2 , если x = 3 y = e-x + b × ln(ax) ï x + b ïî1/(1 + x 2 ), если x > 3 Исходные данные: b; -2≤х≤2 ∆х=1
б) Вычислить ìax - ax , если x £ 0 z = ï 0,2x + e0,5a í ï2a + x 2 , если x > 0 î y = sin 2 z + ln(x + sin x) Считать Y до тех пор, пока выражение под знаком логарифма больше 1. Определить количество у<0, S = åy y³0 Исходные данные: a; х³ 1 Δx= -0,5
в) Вычислить ì ï ax + ln x, если x < 0,5 y = ï 2 - x ísin x + е , если x = 0,5 a = sin (xb) + 2 - x ï x + a , если x > 0,5 î bx Определить количество y≥0 и произведение отрицательных значений а. Исходные данные: b; -1≤x≤1 ∆x=0,2 |
||||
|
5 |
а) Вычислить ìxy + sin 2 xy, если ax > 0 ï z = íex + cos(xy), если ax = 0 ï1 - ln(xy), если ax < 0 î y = a 3 + cosa x + a 2 Исходные данные: a; -0,1≤х≤0,9 |
∆х=0,1 |
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 39
39
|
|
б) Вычислить ì y 2 + a + y , если y £ 1
z = ï ay í ï3ay + cos 2 ay, если y > 1 î F = z 2 0,1+ y + 3z + b 0,1+ y Считать F до тех пор, пока подкоренное выражение не превышает значение Q. Определить количество z>0, S = åz, P = ÕF z£0 Исходные данные: a, b, Q; y³ 0 Δy= 0,5
в) Вычислить ì - 4, если x < -1 f = ïx 2 + 3 + 4, если - 1 £ x £ 1 Z = sin 3 x + | f | í x ï 2 ïî cos(x + 4) , если x > 1 Определить сумму и количество f > 0, произведение значений z. Исходные данные: -2≤x≤2 ∆x=0,2 |
|
6 |
а) Вычислить ìln ax + 1, если a < 1 ï y = í ax + 1, если a = 1 x = sin (ab) + a - b ïa 2 + cos ax, если a > 1 î Исходные данные: b; -1≤а≤2 ∆а=1
б) Вычислить ì x 2 + £ z = ï x + a x , если x 1 í ï ax + 3x sin 3 x, если x > 1 î y = 2bz × sin pa + x + t Считать Y до тех пор, пока подкоренное выражение x+t ³ 0. Определить М=К!, где К - количество вычисленных значений Y. Исходные данные: a, b, t; x£ 5 Δx= -0,5
в) Вычислить ì x 2 + sin 3 x, если a £ x £ b y = ï x - ab , если c £ x £ d f = xа у +1 í3
ï | x | ïî 0, в остальных случаях Определить сумму значений f, количество и произведение y>0. Исходные данные: a, b, c, d; -1≤x≤1 ∆x=0,1 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 40
40
|
7 |
а) Вычислить ìax + b, если ax < c v = ï3 ax + bx, если ax = c t = v + b × cosa - lnx í ïsin (a + b) × x 2 , если ax > c î Исходные данные: а, b, с; -5≤х≤3 ∆х=0,5
б) Вычислить ì a sin 3 x ï 2 , если x ³ 2 z = ïb + (2x + 1) y = z + x + e x3 í ïln(a + x) a , если x < 2 a + bx î a + x Считать Y до тех пор, пока значение Р не станет больше 100. Определить количество вычисленных значений Y, S = åz, P = Õy z>y Исходные данные: a, b; x³ 5 Δx= 0,2
в) Вычислить ì cos 2 x - z, если z > 0 f = ï z + 3x + x3 , если - 1 £ z £ 0 z = x 3 + 5 ln | x | í ï | x + 0,38z |, если z < -1 î Определить сумму значений f < 0, количество f > z и произведение значений z. Исходные данные: -1≤x≤5 ∆x=0,5 |
|
8 |
а) Вычислить ìab × (x + sin 2 x), если x < -5 y = ï + b)/ (1+ x), если - 5 £ x £ 5 z = cosy + a 3 / bx í(a ïln(ab - x) - x 3 , если x > 5 î Исходные данные: а, b; -10≤х≤25 ∆х=5
б) Вычислить ì a 3 ï a + cos 2 (ax) , если x £ 0 5 2 ln az z = í y = px + a + z ï - a ïî( x + a)3 + e 2 , если x > 0 Считать Y до тех пор, пока подкоренное выражение меньше С. Определить N=K!, где К - количество вычисленных значений Y, S = åz z>0 Исходные данные: a, с; x³ 0 Δx= 0,1 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
41
|
|
в) Вычислить ì еsin x , если a 2 x < b ï(x 2 - a) 2 2 3 y = í , если a x = b b = sin x + 3 x ï sin x îïtg (x + a), если a 2 x > b Определить сумму значений y > 0 и произведение значений y < 0, количество вычисленных значений b. Исходные данные: а; -2≤x≤5 ∆x=0,5 |
|
9 |
а) Вычислить ì ïex + ab, если x < 2 ï y = ísinx × (a + b), если x = 2 t = 2y3 + a 2 - y ï ax 2 ï + ln(abx), если x > 2 îb - x Исходные данные: а, b; -4≤х≤2 ∆х=1
б) Вычислить ì1 sin ax + 1, если x ³ 2 ï2 y sin x 2 y = í z = - ï ex 0,2x x + 1 ïî1 + ln 3x , если x < 2 Считать Z до тех пор, пока истинно выражение 2sinx<1,5. Определить количество вычисленных значений z, S = å z , P = Пy z<0 y >0 Исходные данные: a; x³ 0 Δx= 0,2
в) Вычислить ì x + a - a × sin x, если x £ 0 z = ï 2 í (x - a) + x , если x > 0 ïln 5 î y = cos 3 z - 2x 2 + 5 Определить среднее арифметическое отрицательных значений y, количество z > 0. Исходные данные: а; -3≤x≤4 ∆x=1 |
|
10 |
а) Вычислить ì ï1 - sin3 ax, если x > 0 ï y = í- sin(ax2 ), если x = 0 z = a2 + ln(ay) ï a + x ï , если x < 0 î cos ax Исходные данные: а; -3≤х≤5 ∆х=2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 42
42
|
|
б) Вычислить t = ìï(a - b) ln(b + x), если x < 0 z = 1,5t - lnæ x ö íïî 3 ç ax + b ÷ 3 ax + sin ax, если x ³ 0 è ø Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить количество вычисленных значений z, P = Õt, S = åz z>t Исходные данные: a,b; x³ 1 Δx= -0,1
в) Вычислить ïì1+ сos2a, если е -x > 0,1 q = í p sin a , если е -x £ 0,1 a = 2x + x + 4 3 ïî 2 Определить количество q > 0, сумму значений а и произведение значений (q - a). Исходные данные: -0,5≤x≤2 ∆x=0,5 |
|
11 |
а) Вычислить ì a + bx , если x < 4 y = ï + ln bx, если 4 £ x £ 6 b = (x 2 + a)/ ln x ía ï(a - b)× sin x, если x > 6 î Исходные данные: а; -2≤х≤10 ∆х=1
б) Вычислить ì x + a 3 , если x £ 2 z = ï a + 0,3x í ïcos(a + 0,3x) + 5x, если x > 2 î F = 0,2x + sin 3 z 2 x 2 + 1 Считать F до тех пор, пока подкоренное выражение больше 0. Определить количество вычисленных значений F, P = Õz + åF z<0 F >0 Исходные данные: a; x≤3 Δx= -0,2
в) Вычислить ïìx + 3sin p x, если y < 0 z = í 2 îï ln( x - 2) + x 3 , если y ³ 0 y = a 2 - a + x Определить сумму первых пяти значений z и произведение y>0. Исходные данные: а; -1≤x≤4 ∆x=0,5 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 43
43
|
12 |
а) Вычислить ìx 2 + 2xa - e-x , если x > 1 y = ï in 2 x + cos(ax) , если x = 1 x = bz + z +1 ís ïlnx + 0.5a, если x < 1 î Исходные данные: а, b; -1≤z≤1 ∆z=0,1
б) Вычислить ìï(a + b)3 + e x , если x ³ 2 y = í 3 ïîax + ln(b + x), если x < 2 z = a + b ×sin(x + y) 2x - b Считать Z до тех пор, пока FÎ [-2;2]. Определить количество вычисленных значений z, S = åy, F = Õz y>0 Исходные данные: a,b; x³ 0 Δx= 0,5
в) Вычислить ì 0,5х , если q > 0,5 p = ïcos x q = 0,5 + sin 2 x í ïîln(2x) × sin x, если q £ 0,5 Определить среднее арифметическое отрицательных значений р, произведение q >0. Исходные данные: -4≤x≤2 ∆x=1 |
|
13 |
а) Вычислить y = ln a + x 2 ì yax 2 + sin a, если x > a z = ïa 2 - cos(axy ), если x = a í ïsin a × cos xy, если x < a î Исходные данные: а; -3≤х≤3 ∆х=0,5
б) Вычислить ìax 2 + cos a + 2a, если x ³ 0
y = ï x í ï5x + 3 sin x 2 + | x |, если x < 0 î F = ay 3 + æ p + x ö ç ÷ è 3 ø Считать F до тех пор, пока подкоренное выражение больше 0. Определить количество y<0, S = åy, P = ÕF F>0 Исходные данные: a; х£ 4 Δх= -0,2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 44
44
|
|
в) Вычислить ì еsin x , если a 2 x < b ï(x 2 - a) 2 2 3 y = í , если a x = b b = sin x + 3 x ï sin x îïtg (x + a), если a 2 x > b Определить среднее геометрическое положительных значений y, произведение y < 0, количество вычисленных значений b. Исходные данные: а; -2≤x≤5 ∆x=0,5 |
|
14 |
а) Вычислить ì3 ax +1, если x > d ï y = ísin(ax + b), если x = d x = a 2 + 2 bc ï os(bx +1), если x < d îc Исходные данные: а, c, d; -3≤b≤3 ∆b=1
б) Вычислить ì1 + esin xa + 0,5x, если x < 0 y = ï í 1 ïpx + 2 cos xa , если x ³ 0 î F = y + ln(x + ex ) 2x 4 - 1 Считать F до тех пор, пока выражение под знаком логарифма больше 1. Определить количество у>0, P = ÕF, S = åy y<0 Исходные данные: а; х£ 3 Δх= -0,2
в) Вычислить t = ì 0,7 + x, если x > 0 í ln (x + 0,3 ) + x3 , если x £ 0 î y = 2t x + 5x Определить сумму значений t > 0, произведение значений y < 0, количество y > t. Исходные данные: -5≤x≤5 ∆x=1 |
|
15 |
а) Вычислить ì ï b3 + x, если x < a 2 ï y = í x5 - ax, если x = a 2 b = sin x + cos(xa) ï ï ax 4 + 4x3 2 ïî bx , если x > a Исходные данные: а; -2≤х≤10 ∆х=0,2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 45
45
|
|
б) Вычислить ìï3cos x 2 + 3,4a, если x > 2 p y = í z = 8,36 sin y + a 2 + ïî3 1 + x + e-x+1, если x £ 2 2 Считать Z до тех пор, пока подкоренное выражение меньше Q. Определить количество вычисленных значений Z, P = Õy, S = åz z>0 Исходные данные: x, Q; a³ 0 Δa= 0,5
в) Вычислить ìln(x + 1) - 2x3 , если x > 0,5 z = í y = z 2 + tgx î x + 1 + sin 2 x, если x £ 0,5 Определить сумму значений z, количество y > 0 и y < 0. Исходные данные: -3≤x≤2 ∆x=0,2 |
|
16 |
а) Вычислить ìa + sin x, если yx > a z = ï a + x 2 , если yx = a í ïln a + x , если yx < a î y = ìsin ax - cos a, если a ³ 0.2 í îcos ax + sin a, если a < 0.2 Исходные данные: х; 0≤а≤10 ∆а=0,2
б) Вычислить ì x 2 y = ï0,5a 1 - x + sin xa, если x £ 1 z = 2,3y + x í 2x 2 + 1 ïî4a + e -x + 2 cos 3 x 2 , если x > 1 Считать Z до тех пор, пока подкоренное выражение имеет положительное значение. Определить количество и сумму положительных значений Z, P = Пу у<0 Исходные данные: а; х£ 10 Δх= -0,5
в) Вычислить ïì2 - 1 , если cos x £ 0,3 2 y = í x b = 2 sin (yx) + 10 ïî 3x × tgx, если cos x > 0,3 Определить F = N!, где N – количество вычисленных значений y, сумму отрицательных значений b. Исходные данные: -3≤x≤3 ∆x=1 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
46
|
17 |
а) Вычислить ìcos xa , если x < a ï xa ìx3 - c, если x > sin x f = ï in xa, если x = a a = ï ís í 3 ïln xa +1.5x, если x > a ïîx + c, если x £ sin x ï î Исходные данные: с; -1≤х≤10 ∆х=0,1
б) Вычислить ïì | a - x | ln(a + x), если x < 2 b = í ïîa + x3 , если x ³ 2 y = sin 2 b + cos(x - p ) + 1 Считать Y до тех пор, пока значение переменной Р меньше 10. Определить P = Õ y, С = åb + å y b>0 y<0 Исходные данные: a; x³ 0 Δx= 0,1
в) Вычислить ì1.5 + b × sin 3 x, если x £ 3 y = ï 8.5 f = y 2 + tgx í ï(x - b) , если x > 3 î Определить количество f<0 и f>0, сумму отрицательных значений у. Исходные данные: b; -2≤x≤4 ∆x=1 |
|
18 |
а) Вычислить ì 2 ïln x + sin bx , если x < 1 ï z = í(1 + x 2 )× cos b, если x = 1 y = z 3 + b × cos z ïb × ex , если x > 1 ï î Исходные данные: b; -3≤х≤3 ∆х=1
б) Вычислить ìax 3 + 5x - 3a , если x ³ 2 ï 3 3 y = í 2x - cos b С = 1- sin y ï ln x ln(x 3 - x 2 + x) ï(x + 3) × e x - , если x < 2 î bx Считать C до тех пор, пока выражение под знаком логарифма больше 1. Определить S = åC, P = Õy , количество С>0. y>0 Исходные данные: a,b; х£ 3 Δх= -0,2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 47
47
|
|
в) Вычислить ìx 2 × sin a + a , если x £ 1 zï x í ïîa × tg 2 x, если x > 1 y = cos 3 z + 2.3 - ax Определить произведение положительных значений y, количество и сумму z Î [c, d]. Исходные данные: a, c, d; -2≤x≤2 ∆x=0,2 |
|
19 |
а) Вычислить ìln x - b 2 , если x < 0.2 ï z = ísin x + bx , если x = 0.2 ïb + ln x, если x > 0.2 î b = (a + sin x)2 / cos x Исходные данные: а; -8≤х≤8 ∆х=1
б) Вычислить ì x × sin px + 2a 3 , если x > 0 y = ï 2 í 1.5a ï1 + x 3 - , если x £ 0 î 2x z = y + cos(y - p ) + ln(x + 3x 2 ) sin 2 x Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить количество вычисленных значений z, P = Õz, S = åy. y0 Исходные данные: a; х³ 0 Δх= -0,3
в) Вычислить ïìsin(ln x ), если x £ 2 y = í 1 z = 2tg 2 y + x îï3 x + e x-4 , если x > 2 Определить количество и сумму положительных значений y и z. Исходные данные: -1≤x≤10 ∆x=1 |
|
20 |
а) Вычислить y = e0.5x + a + x ìb3 × x, если b < x ï ï b 2 a = íb + x , если b = x ï îïb3 × sin x, если b > x Исходные данные: х; -8≤b≤16 ∆b=1 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
48
|
|
б) Вычислить ì3 ax + 2.5ax, если x < 0 2 y = ï 2 z = 36,5y 3 - 0,9 sin x
í1 x 1,5y - ln(xy) ï2 cos x + x -1 , если x ³ 0 î Считать Z до тех пор, пока истинно выражение S<5. Определить количество вычисленных значений z>0 и y<0, S = åz z<0 Исходные данные: a; х³ 1 Δх= 0,5
в) Вычислить ì x , если x + a > 2 y = ï(x + a ) í ïax 2 + sin 3 x + b, если x + a £ 2 î a = x × b - 1 x -1 Определить количество и сумму y < 0, произведение значений a. Исходные данные: b; -5≤x≤5 ∆x=1 |
|
21 |
а) Вычислить ìz - ab3 , если z < 4 y = ïz 2 + abx, если 4 £ z £ 6 z = 1.5x + sin 2 x í ïbz + ln az , если z > 6 î Исходные данные: a, b; -2≤x≤20 ∆x=2 б) Вычислить z = ïìln(ax +1) + ax , если x £ 3 í 2 ïî(ax) + cos | ax |, если x > 3 F = 2,72z + z 2 ×sin(x + a) Считать F до тех пор, пока истинно выражение x+a≥0. Определить количество и сумму положительных значений F, P = Õz . z<0 Исходные данные: a; x£ 2 Δx= -0,4
в) Вычислить ì x + sin(x + a), если x < 2 y = ï (x + a) + 2.5, если x = 2 íln ïe -x + ax + b3 , если x > 2 î z = a + cos 3 y Определить количество вычисленных значений z, произведение значений y, которые больше (z – y)2. Исходные данные: а, b; -4≤x≤2 ∆x=1 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
49
|
22 |
а) Вычислить ìb × a + x , если x < 1 ï y = íln bx + a + x , если 1 £ x £ 5 ï a + x × (b - x), если x > 5 î z = y 2 + cos 2 y 3 Исходные данные: a, b; -2≤x≤8 ∆x=0,1
б) Вычислить ì4x 0,6 - 2 ln x - 7, если x < 10 y = ï í p ï1 - cos 2 x + 2a sin x, если x ³ 10 î Q = 2,45 y × ln(a 3 - sin(ax)) Считать Q до тех пор, пока выражение под знаком логарифма больше 0. Определить количество Q>0, P = ÕQ, S = åy. y£0 Исходные данные: a; х £ 5 Δх= -0,5
в) Вычислить ì x ï2x 3 + , если x £ 3 z = í x -1 y = 0.25z + ln z 2 ï 7 + cos x 2 , если x > 3 ïî(x + 6) Определить количество вычисленных значений z>0 и z<0, произведение значений y. Исходные данные: -3≤x≤3 ∆x=0,2 |
|
23 |
а) Вычислить ìcos x2 + a, если cos x > sin x f = ï in2 xa, если cos x = sin x ís ïln(x + a), если cos x < sin x î a = cos2 x + 1 bx Исходные данные: b; 0,2≤x≤0,6 ∆x=0,1
б) Вычислить ìïa 2 + 0,2 | sin ax |, если ⁝ x ³ 1 z = í îï 2x 2 - 3x + e-ax , если x < 1 y = a × cos x 2 + ln sin 3z Считать Y до тех пор, пока истинно выражение F<Q. Определить количество z≥0, F = åy . Исходные данные: a, Q; x³ 1 Δx= 0,2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 50
50
|
|
в) Вычислить ìï(x + 0.5)2 + cos ax 3 , если x ³ 1 y = í ïîx - 0.25 x +1, если x < 1 x 3 z = + ln x 2 y - 5 Определить среднее арифметическое отрицательных значений y, количество вычисленных значений z. Исходные данные: а; -1≤x≤1 ∆x=0,1 |
|
24 |
а) Вычислить ìt × e -x + 5t 3 , если x < 0 y = ïx 2 + ln t, если x = 0 í ïx + sin xt, если x > 0 î t = x 3 + 0.5 cos b x +1 Исходные данные: b; -2≤x≤8 ∆x=0,5
б) Вычислить ìïsin a 2 + cos(a - p ) + x3 , если x > 0 y = í ïî3 × ln(1 + ex ) + | x |, если x £ 0 F = p sin 2 y + ln(2x - x 2 ) 2 Считать F до тех пор, пока выражение под знаком логарифма больше 0. Определить количество F>0, S = åy, P = ÕF y<0 Исходные данные: a; x£ 1 Δх= -0,1
в) Вычислить ì2 sin 2 x + e -x , если x > 0 y = ï í a ïtgx + x 3 , если x £ 0 î z = (x - 2)× 3 x 2 + 7.2 y Определить сумму отрицательных и произведение положительных значений y, количество вычисленных значений z ³ 0. Исходные данные: а; -2≤x≤2 ∆x=0,4 |
|
25 |
а) Вычислить
ìï x - c 2 , если x £ a y = í ïîsin(x + c), если x > a y 2 + sin y z = ln(x - c) Исходные данные: а, с; -4≤x≤4 ∆x=0,4 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 51
51
|
|
б) Вычислить ì e x ï , если x ³ 0 y = í1+ ln 3x z = 3 pa 2 + x + y × cos 2 x 3 ï2 sin 2 p x + 2.5 x , если x < 0 î 2 Считать Z до тех пор, пока подкоренное выражение не превысит значение b. Определить количество z<0, S = åz, P = Õy z³0 y>0 Исходные данные: a, b; х ³ 0 Δх= 0,2
в) Вычислить ïì33 1 + x - 5 ln x, если x £ 2 y = í 2 îïx sin x 2 - e -x , если x > 2 z = sin 2 y + cos(x - 1) Определить количество вычисленных значений y > 0 и z < 0, сумму и произведение вычисленных значений z. Исходные данные: -4≤x≤1 ∆x=0,2 |
|
26 |
а) Вычислить ì5 a + bx , если x < 4 y = ï - ln bx, если 4 £ x £ 6 b = (х 2 + a)/ ln x ía ï(a - b)× sin x, если x > 6 î Исходные данные: а; -2≤x≤10 ∆x=1
б) Вычислить ìa 3 + x 1 + sin ax , если x £ 1 y = ï í b ïa cos 2 x + , если x > 1 î sin x F = 2,72 y + 2a 2 ln(2 + 2x + 2x 2 ) Считать F до тех пор, пока выражение под знаком логарифма больше 0. Определить количество F>0, P = Õy, S = åF y>0 Исходные данные: a, b; х£ 4 Δх=-0,5
в) Вычислить ì y - 1 , если x £ 2 z = ï 4 1- x y = (1+ x 3 )+ cos b í x 2 ï (x + 2)5 - y - 6x 2 , если x > 2 î Определить сумму и количество вычисленных значений y, произведение вычисленных значений z>0. Исходные данные: b; -1≤x≤1 ∆x=0,1 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 52
52
|
27 |
а) Вычислить ìbx 2 + ln(ax), если x < 1 ï y = ía + bx, если 1 £ x £ 3 ï îa x 3 - b + e x , если x > 3 z = 5x + 3sin 3 y Исходные данные: а, b; -1≤x≤5 ∆x=0,2
б) Вычислить ì2,5xa 3 + cos 2 x, если x > 0 y = ï z = a ×cos ax + sin y
í æ p ö ïlnç cos 2 xa ÷ + 0.2, если x £ 0 3 î è ø Считать Z до тех пор, пока подкоренное выражение больше 0. Определить количество z>0, P = Õy, S = åz y>0 Исходные данные: a; х³ 2 Δх= -0,5
в) Вычислить ì3x + 5 sin 2 x, если x > 1 y = ï z = 3 1 + x + 2
í .5 x , если x £ 1 5y ï0 1 - x î Определить разницу между суммой и произведением положительных значений y, количество вычисленных значений z. Исходные данные: -1≤x≤5 ∆x=0,2 |
|
28 |
а) Вычислить ì3 ax + b, если b > 1 y = ï + b, если b = 1 x = cos a + 2 bc ícx ïtg (bx +1), если b < 1 î Исходные данные: а, с; -3≤b≤3 ∆b=1
б) Вычислить ì2 x + 0.1ab + x , если x £ 2 y = ï x + 1 í ïsin x + 1 + cos 2 x 3 , если x > 2 î z = b 2 × ln(0,1 + x) - 3 y + x 2 Считать Z до тех пор, пока выражение под знаком логарифма больше 0. Определить количество вычисленных значений Y, P = Õz, S = åz z<0 Исходные данные: a, b; х ³ 0 Δх= 0,1 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 53
53
|
|
в) Вычислить ìï3 cos 2 x + ln(4 + x), если x £ 5 z = í ïî3 x 2 + e -x+1 , если x > 5 y = sin x 3 - tg 2 z Определить среднее геометрическое положительных количество и сумму вычисленных значений у. Исходные данные: -10≤x≤10 ∆x=2 |
значений |
z, |
|
|
29 |
а) Вычислить ì 0,2 + sin x , если x £ a ï y = ï cosæ 1 ö если a < x < b í ç xa ÷, ï è ø ïln ax , если x ³ b î z = x + 3 y 2 + 1 Исходные данные: а, b; -5≤х≤2 ∆х=0,2
б) Вычислить ì1 x 2 + 1 - 6.5a, если x > 2 1 - sin y y = ï2 z = í ln(x3 - x 2 + x) ï1.2 a + cos x + x3 , если x £ 2 î Считать Z до тех пор, пока выражение под знаком логарифма больше 1. Определить количество вычисленных значений z>0, P = Õy, S = åz y>0 Исходные данные: a; х£ 3 Δх= -0,2
в) Вычислить ì1+ esin x , если x ³ 2 y = ï í 1 ïln 2 + 2x + x 2 , если x < 2 î z = 4 y 0.6 - 2 x Определить количество у £ 0, сумму и произведение z > 0. Исходные данные: -2≤x≤2 ∆x=0,2 |
|||
|
30 |
а) Вычислить ì x + 2 , если x < 1 ï sin(b + x) ï z = í(1+ x 2 )×cos b, если x = 1 y = z 3 + ïb × e x , если x > 1 ï ïî Исходные данные: b; -3≤х≤3 ∆х=1 |
b + cos z |
||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 54
54
 б) Вычислить
б) Вычислить
ì1- e-x + cos pa,
![]()
![]() y = ï
y = ï
![]()
![]() ïb sin px + ,
ïb sin px + ,
если
если
x > 0
x £ 0
î 2x
![]() z = 8,3 sin y +
z = 8,3 sin y +
Считать Z до тех пор, пока подкоренное выражение больше 0. Определить количество вычисленных значений z<0,
P = Õz,
z>0
S = åy
Исходные данные: a, b; х³ 1 Δх= -0,2
в) Вычислить
![]() x × (e 2x +1.5),
x × (e 2x +1.5),
если
x > 2
y = íïî1.8
![]() z =
y +
z =
y +
- sin 2 x,
- ![]()
![]() cos x
cos x
y
если
x £ 2
Определить количество и сумму отрицательных значений z и произведение вычисленных значений у.
Исходные данные: -2≤x≤5 ∆x=1
Контрольные вопросы
1. Что такое алгоритм?
2. Какими свойствами обладает алгоритм?
3. Какие геометрические фигуры могут использоваться в блок- схеме циклического алгоритма?
4. Какие действия необходимо выполнить для организации циклического алгоритма?
5. Какие существуют способы организации циклических структур?
6. Что такое параметр цикла?
7. Какие используются операторы циклов для организации циклических вычислительных процессов в программе?
8. Какие операторы циклов используются для программирования циклов с неизвестным числом повторений?
9. Что такое составной оператор? Привести примеры его использования.
10. Каковы отличия циклических структур различного вида?
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.