Лабораторная работа № 5. Изучение свойств линейного нейрона и линейной нейронной сети

Лабораторная работа № 5. Изучение свойств линейного нейрона и линейной нейронной сети

Цель работы

Изучить свойства линейного нейрона и линейной нейронной сети.

Основные теоретические положения

            Модель нейрона. Искусственные нейронные сети (НС) представляют собой простейшие математические модели мозга. Понять основные принципы построения НС можно, рассматривая их как совокупность (сеть) отдельных структур (нейронов). Очень грубо структуру биологического нейрона можно описать следующим образом. Нейрон имеет сому – тело, дерево входов – дендриты, выход – аксон. На соме и на дендритах распола­гаются окончания аксонов других нейронов, называемых си­напсами. Принятые синапсами входные сигналы стремятся либо возбудить нейрон, либо затормозить. Когда суммарное возбуждение достигает некоторого порога, нейрон возбуждается и посылает по аксону сигнал другим нейронам. Каждый синапс обладает уникальной синаптической силой, которая пропорционально своему значению изменяет передаваемый на нейрон входной сигнал. В соответствии с приведенным описа­нием математическая модель нейрона представляет собой суммирующий пороговый элемент (рис. 1).

                   Ошибка! Ошибка связи.

Рис. 1. Искусственный нейрон

         Формула срабатывания нейрона:

            Алгоритм обучения по дельта-правилу. Обучение НС происходит на некоторой обучающей выборке, для каждого образца которой определяются и сравниваются с желаемыми значениями все текущие выходы. Если разница недопустима, то веса изменяются. Окончанием обучения считается ситуация, когда общая ошибка на всех образцах допустима.

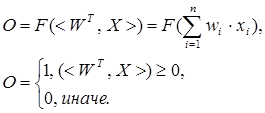
         Все алгоритмы обучения нейросетей являются разновидностями алгоритма обучения по методу коррекции ошибки, которая осуществляется по-разному. Идея изменения весов НС сводится к нахождению общей меры качества сети, в качестве которой обычно выбирают функцию ошибки сети. Тогда, чтобы подобрать нужные веса, необходимо минимизировать функцию ошибки. Самым распространенным методом поиска минимума является метод градиентного спуска. Для случая функции с одной переменной веса изменяются в направлении, противоположном производной, т. е. справедлива формула:

где  h – некоторый уровень обучения, шаг изменения;

F'(W) – производная функции качества НС для одной переменной.

         Для функции F от n переменных и единичного вектора е в пространстве Rⁿ ||е|| = 1, , дифференциал выражается формулой:

.

         Для случая е = (0, 0...1...0) определим частный дифференциал:

.

         Таким образом, антиградиент – это набор следующих дифференциалов:

         Для определения обобщенной функции ошибки рассмотрим обучающую выборку {(х^k, y^k)}, где k = 1, ..., К. Накопленная по всем эпохам ошибка:

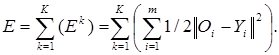
         Формула модификации весов НС:

уточняется для различных видов функции активации. Для линейной функции F(t) = t, НС формирует каждый выход как скалярное произведение весов на вектор входов:  и градиент будет равен:

где Y_i – желаемый выход; O_i – полученный выход; X – вектор выхода.

         Таким образом, получаем формулу изменения весов:

         Если значением  назвать разницу (Y_i – О_i), то получим формулу:

что является алгоритмом обучения по -правилу.

         Описание основных функций. Для работы с нейронными сетями необходимо инсталлировать MATLAB и обладать первоначальными знаниями относительно языка системы. Поскольку MATLAB представляет собой интерпретатор, то обучение инструментарию нейронных сетей заключается в основном в изучении функций и их параметров. Узнать возможности нейрона как классификатора простых линейно сепарабельных задач можно путем проведения экспериментов с моделью одного линейного нейрона.

         Функция newp. Для того чтобы создать нейрон, используют функцию newp, имеющую следующий синтаксис:

где PR – матрица минимальных и максимальных R входных эле­ментов; S – количество нейронов (при создании одного нейрона S = 1); TF – функция активации (transfer function); LF – имя функции обучения нейрона.

         В случае если параметры функции newp не заданы, их зна­чения определяются посредством ввода значений в диалого­вые окна. Построенный нейрон характеризуется функциями весов (weight function), входов сети (net input function) и оп­ределенной функцией активации. Функция весов – это ум­ножение весов на входной сигнал, функция входов сети – их сумма. Веса задаются как для входов нейрона, так и для фик­сированного входа, задающего порог срабатывания (bias). Вектор весов инициализируется нулями. Для обучения ис­пользуются функции, рассмотренные ниже.

         Функция learnp настраивает веса нейрона. Синтаксис функции обучения довольно сложен:

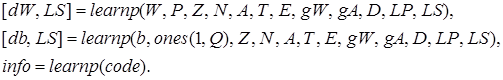
         Функция learnp (W, P, Z, N, A, T, E, gW, gA, D, LP, LS) имеет несколько входов, где вектор W – вектор весов; Р – вектор входов; Z – вектор взвешенных входов; N – вектор сети; А – вектор выхода; Т – вектор желаемых выходов; Е – вектор ошибок; gW – вектор изменения весов; gA – изменения вы­ходов. Функция возвращает значения: dW – изменения мат­рицы весов; LS – новый уровень обученности.

         Функция learnp может быть использована с параметрами по умолчанию:

         Использование пустого списка [ ] означает параметр по умолчанию.

         Функция learnp вычисляет изменение весов dW для заданного нейрона в соответствии с правилом обучения персептрона:

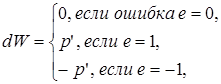
т.е. .

         Функция learnpn настраивает нормализованные веса:

         Функция learnpn вычисляет изменение весов dW для данного нейрона и его входа Р и ошибки Е в соответствии с нор­мализованным правилом обучения персептрона:

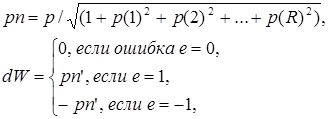
т.е. .

         Линейный нейрон имеет одно существенное ограничение. Входные векторы должны быть линейно разделимы. Если векторы невозможно отделить прямой или гиперплоскостью, то персептрон не способен решить задачу классификации.

         Функция adapt адаптирует НС к условиям задачи:

         Параметры функции adapt: net – имя сети; Р – входы сети; T – желаемый выход; Р_i – исходные условия задержки; A_i – ис­ходные условия задержки для слоя. Функция возвращает па­раметры адаптированной сети net.adaptParam: net – изменен­ная сеть; Y – выход сети; Е – ошибки сети; Pf – условия за­держки входов; Af – условия задержки слоя. Параметры Р_i и Pf необязательные и необходимы только для сетей, имеющих задержки на входах и слое.

         Функция train также обучает НС и использует следующий синтаксис:

         Функция train имеет следующие параметры: net – сеть; Р – входы сети;    Т – желаемый выход; Р_i – исходные условия задержки входа; A_i – исходные условия задержки слоя.

         Функция  sim имитирует нейронную сеть:

где net – сеть; Р – входы сети; P_i — исходные условия задержки входов сети;   A_i – исходные условия задержки слоя. Функция возвращает Y – выходы сети;   Pf – окончательные условия задержки входов; Af – окончательные условия задержки слоя.

         Функции активации. Ниже представлены назначения этих функций.

         Функции графического интерфейса и вспомогательные функции. Назначение этих функций представлено ниже.

            Структура данных описания нейронных сетей. Структура данных net – это описание обученной НС. Обучение осуществляется в соответствии со следующими параметрами, значения которых либо устанавливаются пользователем, либо по умолчанию.

            Структура данных описания адаптированной НС net.adaptfcn включает в себя следующие поля net.adapt.param: NET – адаптированная НС; Y – выходы НС; Е – ошибки НС; Pf – окончательные входные значения задержек;                Af – окончательные выходные задержки; TR – результат обучения (эпохи и целевая ошибка). Проведем в среде MATLAB toolbox эксперименты, используя рассмотренные функции.

Порядок выполнения работы

Пример 1. Создание нейронов, реализующих функции логического И и логического ИЛИ

         Создадим нейрон с одним двухэлементным входом (интервалы первого и второго элементов [0; 1]). Определим два первых параметра функции newp, а в качестве значений третьего и четвертого параметра (типа функции активации и имени процедуры обучения) воспользуемся значениями по умолчанию.

% создание нейрона с одним двухэлементным входом (интервал

% первого элемента [0; 1] и интервал второго элемента [-2; 2]

net = newp([0 1; -2 2], 1);

         Для того чтобы исследовать поведение нейрона, необхо­димо имитировать его работу с помощью функции sim. Для определения последовательности значений входа создадим последовательность Р1.

% создание последовательности значений входа

P1 = {[0; 0] [0; 1] [1; 0] [1; 1]};

% имитация работы нейрона net на последовательности входов Р

% желаемых выходов – Т1, которая позволит нам провести адаптацию

% нейрона (обучить его) через 20 проходов.

Y = sim (net, P1);

% создание последовательности выходов

T1 = {0, 0, 0, 1};

% установка количества проходов (циклов) адаптации

net.adaptParam.passes = 20;

% адаптация нейрона net для обучающей выборки <Р1; Т1>

net = adapt (net, P1, T1);

% симуляция работы нейрона net на последовательности входов  P1

Y = sim (net, P1);

            В результате мы получим нейрон, выполняющий функцию логического И.

         Для переобучения нейрона на выполнение функции ИЛИ переопределим входы Р и выходы Т.

% создание последовательности входов

P2 = [0 0 1 1; 0 1 0 1];

% создание последовательности выходов (реакций) для нейрона,

% выполняющего функцию логического ИЛИ

T2 = [0, 1, 1, 1];

% Инициализируем нейрон, обучим его на 20 проходах (эпохах)

% инициализация нейрона net

net = init (net);

% имитация работы нейрона net на последовательности входов Р2

Y = sim (net, P2);

% установка количества проходов

net.trainParam.epochs = 20;

% обучение нейрона net на обучающей выборке <Р2, Т2>

net = train(net, Р2, Т2);

% имитация работы нейрона net на последовательности входов Р2

Y = sim (net, P2);

         Функция train выводит график обучения нейрона (рис. 2).

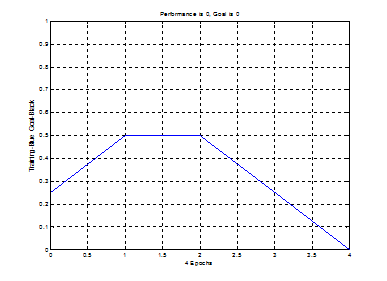
Рис. 2. График обучения нейрона

Для случайного изменения весов и порога срабатывания используем функцию init. По умолчанию для создаваемого нейрона указана функция hardlim.

Пример 2. Обучение нейрона классификации векторов на две         категории

         Начнем с классификации векторов на основе двухвходового нейрона. Будем использовать функцию newp для создания нейрона, sim для имитации его работы, adapt для адаптации (обучения) нейронной сети. Обучим двухвходовый нейрон классифицировать входные векторы на две категории.

% определение четырех двухэлементных входов

P = [ -0.5 -0.5 0.4 -0.2; -0.5 0.5 -0.4 1.0];

% зададим желаемые выходы нейрона для определенных векторов

T = [1 1 0 0];

% изобразим входные векторы (точки) на плоскости:

plotpv(P, T);

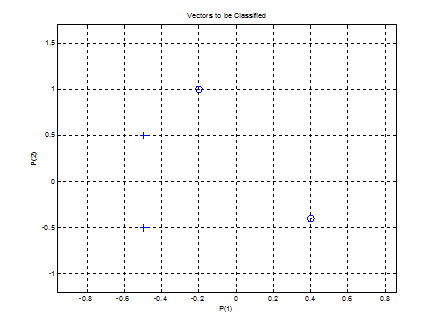
Рис. 3. Исходные векторы, предназначенные

для классификации нейроном

         Каждый из четырех входных векторов на плоскости Р определяется двумя координатами, представленными как двухэлементные столбцы в матрице Р (рис. 3).

         Создадим один линейный нейрон с двумя входами, значения которых лежат в интервале [-1, 1].

% создание линейного нейрона с двумя входами из интервала [-1, 1]

net = newp([-1 1; -1 1], 1);

         Нейрон по умолчанию имеет функцию активации hardlim, и такой нейрон разделяет входные векторы прямой линией.

         Определим координаты линии классификации: веса (IW) и порог срабатывания нейрона (b).

% получение управляющей структуры linehandle для изображения

% разделяющей линии в координатах весов (IW) и порога

% срабатывания нейрона (b)

linehandle = plotpc (net.IW{1}, net.b{1});

% изображение разделяющей прямой

plotpc(net.IW{1}, net.b{1});

         Если исходным весам задать нулевые значения, то любые входы дадут одинаковые выходы и линия классификации не будет видна на плоскости. Проведем обучение:

% очистка координатных осей

cla;

% изображение входных векторов двух категории, категория задается

% элементами вектора Т

plotpv(P, T);

% получение управляющей структуры linehanctle

linehandle = plotpc(net.IW{1}, net.b{1});

% присвоение начального значения ошибки

E = 1;

% инициализация нейрона

net = init (net);

% получение управляющей структуры linehandle

linehandle = plotpc (net.IW{1}, net.b{1});

% организация цикла, пока ошибка не равна 0

while (mse(E))',

% адаптация нейрона net на обучающей выборке <Р, Т>,

% функция возвращает адаптированный нейрон net,

% выход Y, ошибку Е

[net, Y, E] = adapt (net, P, T);

% изображение разделяющей прямой нейрона после адаптации

linehandle = plotpc(net.IW{1}, net.b{1}, linehandle);

% очистка окна графиков

drawnow;

% конец цикла while

end;

         Функция adapt возвращает новый объект – сеть, которая выполняет классификацию, выход сети и ошибку (рис. 4).

         Проведем классификацию нового вектора с помощью обученного нейрона на основе функции sim. Определим но­вый вектор P.

% определение вектора Р

P = [0, 6; 1, 1];

% имитация работы нейрона net, получение отклика нейрона а

а = sim (net, P);

% изображение входа P, отнесенного нейроном к категории а

plotpv (P, а);

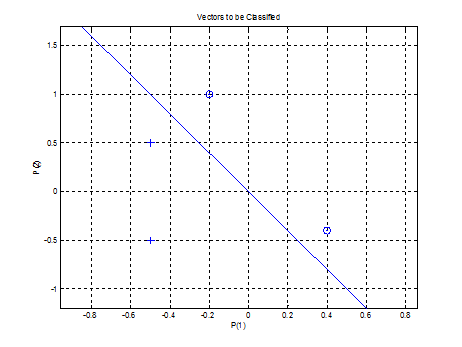
Рис. 4. Прямая, разделяющая исходные векторы на классы

         Обученный нейрон можно использовать для классификации любого вектора:

% включить режим добавления графиков в графическом окне

hold on;

% изображение входных точек в соответствии с категориями Т

plotpv(Р, Т);

% изображение разделяющей поверхности

plotpc (net.IW{1}, net.b{1});

% отключение режима добавления графиков

hold off;

         Нейрон классифицирует новую точку как принадлежащую категории «0» (представлена кружком), а не категории «1» (представлена +).

         Пример 3. Создание слоя линейных нейронов

         Рассмотрим последовательность из 10 шагов (для выхода T1, который известным образом зависит от входов Р1):

% последовательность входов

P1 = {-1 0 0 0 1 1 -1 0 -1 1};

% последовательность выходов

T1 = {-1 -1 1 0 1 2 0 -1 -1 1};

         Используем функцию newlin, чтобы создать нейрон со значениями входа в интервале [-1; 1], задержками входа от 0 до 1 и уровнем обучения 0,1.

% создание линейного слоя из одного нейрона со значениями входа

% в интервале [-1; 1], задержками входа от 0 до 1

% и уровнем обучения 0,1.

net = newlin ([-1 1], 1, [0 1], 0.1);

         Адаптируем нейрон к задаче одним проходом через последовательность входа. Измерим среднюю квадратичную ошибку с помощью функции mse(e).

% адаптация нейрона к последовательности P1

[net, y, e, pf] = adapt (net, P1, T1);

% измерение ошибки

mse (e)

         Получим довольно большую ошибку. Вновь адаптируем сеть на 10 шагах последовательности, используя предыдущее значение pf как новое исходное значение задержки:

P2 = {1 -1 -1 1 1 -1 0 0 0 1};

T2 = {2 0 -2 0 2 0 -1 0 0 1};

% адаптация с начальным вектором задержки pf

[net, y, e, pf] = adapt (net, P2, T2, pf);

mse (e)

         Адаптируем сеть на 100-разовом прогоне последовательности:

% формирование новой последовательности входов

P3 = [P1 P2];

% формирование новой последовательности выходов

T3 = [T1 T2];

% установка количества проходов

net.adaptParam.passes = 100;

% адаптация нейрона

[net, y, e] = adapt (net, P3, T3);

         Получим приемлемую ошибку, значит, сеть обучена зависимости входов от выходов.

Контрольные вопросы

1 Что представляет собой математическая модель нейрона? Как выглядит формульное представление алгоритма обучения по дельта-правилу?

2 Какое ограничение имеет линейный нейрон?

3 Можно ли обучить линейный нейрон выполнять логиче­скую функцию исключающего ИЛИ?

4 Какие функции используются для настройки весов персептрона в среде MATLAB? В чем их отличие?

Скачано с www.znanio.ru