Лабораторная работа № 8. Изучение продукционных моделей

Лабораторная работа № 8. Изучение продукционных моделей

Цель работы

Изучить методы решения задач с использованием продукционных моделей. Ознакомиться с методами прямого и обратного вывода.

Основные теоретические положения

Основным элементом продукционной модели является продукция, под которой понимается выражение «Если …, то ….», представленное в виде следующей конструкции:

,

где  – имя продукции,  – сфера применения продукции,  – ядро продукции,  – антецедент,  – консеквент,  – постусловие продукции.

Совокупность согласованных продукционных правил (продукций) вместе с механизмом вывода, устанавливающим порядок использования продукционных правил для решения поставленной задачи, называется  продукционной моделью.

Механизм вывода представляет собой программу, управляющую правилами-продукциями в процессе решения задачи и, в частности, устанавливающую порядок просмотра правил и их применения к фактам, имеющимся в БД, с целью решения поставленной задачи. По способу управления продукционными правилами различают механизмы с прямым и обратным выводом.

Прямой метод вывода в продукционных моделях  реализуется посредством преобразования отдельных фактов БД в конкретные значения истинности предусловий правил продукций, после чего те из продукций, для которых становятся истинными соответствующие предусловия, генерируют заключения своих правых частей. Эти заключения принимаются в качестве новых фактов БД. Далее процесс вывода рекурсивным образом повторяется до тех пор, пока не будут найдены заключения, являющиеся целевыми в контексте решаемой задачи.

Обратный вывод реализуется посредством подстановки некоторых интересующих нас заключений в качестве целевых фактов (гипотез) в правые части продукционных правил, после чего те из продукций, правые части которых становятся истинными, генерируют предусловия своих левых частей. Эти предусловия принимаются в качестве новых гипотез, и процесс вывода рекурсивным образом повторяется до тех пор, пока не будут получены факты, имеющиеся в исходной БД и подтверждающие выдвинутые гипотезы.

Описание процесса системного моделирования. Процесс системного моделирования с использованием продукционных моделей рассмотрим для достаточно часто встречающегося на практике класса систем, называемых дискретно-динамическими системами. Для таких систем процесс функционирования отражает поведение системы во времени и может быть представлен как последовательное изменение ее состояний. Если система изменяет одно свое состояние на другое состояние, то принято говорить, что система переходит       из одного состояния в другое. Правила перехода системы между состояниями задаются продукционными правилами, входящими в продукционную модель системы. Задача системного моделирования для дискретно-динамических систем представляет собой задачу многошагового принятия решений и заключается в поиске такой последовательности правил, которая переводит систему из исходного состояния в целевое некоторым оптимальным образом в соответствии с заранее установленным критерием.

Следует отметить, что к описанной выше задаче многошагового принятия решений сводится достаточно широкий круг оптимизационных задач, с которыми на практике сталкиваются специалисты. В частности, к задаче многошагового принятия решений в пространстве состояний сводятся большинство задач динамического программирования: задачи планирования расписаний, управления маневровыми работами, прогнозирования поведения сложных процессов и т.п.

В наиболее общем виде процесс системного моделирования с использованием продукционных моделей сводится к следующим этапам:

1 Определение пространства состояний системы и постановка задачи принятия решений в виде поисковой задачи в пространстве состояний.

2 Определения перечня продукционных правил, обеспечивающих переход (перевод) системы из одного состояния в другое.

3 Задание механизма вывода (прямого, обратного, смешанного).

4 Задание начального состояния системы в виде множества известных фактов и запуск механизма вывода в качестве механизма моделирования и генерации решений.

Из приведенных выше четырех этапов наименее формализуемыми являются первые два. Их конкретное содержание и способ реализации зависят от предметной области и специфических особенностей решаемой задачи. Этапы   3 и 4 поддаются формализации и могут быть реализованы в компьютере с использованием имеющихся программных средств и, в частности, с использованием языка программирования высокого уровня MATLAB.

Пример

Процесс построения продукционной модели рассмотрим на примере известной задачи о маневрировании, являющейся, в некотором смысле, модельной задачей многошагового принятия решений.

Имеется участок железной дороги, на котором находятся локомотив L и вагоны A, B, C, D в порядке, показанном на рисунке 1.

Локомотив может тянуть и толкать вагоны в прямом и обратном направлении, стрелку можно переводить в любое положение, а вагоны можно произвольно отцеплять, оставлять на пути, а затем сцеплять. Требуется найти последовательность действий (маневрирование), в результате которой вагоны и локомотив окажутся на нужном пути в заданном  порядке, например, на пути П2  в порядке BACD.

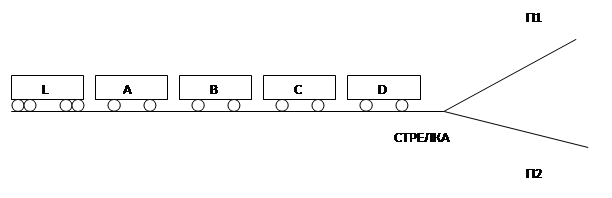
Рис. 1

Этап 1 Введем в рассмотрение пространство состояний, каждое из которых характеризует некоторый порядок расположения вагонов на пути. Решение задачи представим в виде многошагового процесса перевода системы из одного состояния в другое путем маневрирования. Продукционные правила должны отражать технологические действия, связанные с передвижением локомотива, отцепом и прицепом к нему части вагонов.

Этап 2 Наиболее простым технологическим действием является маневр, в результате которого на некотором пути от локомотива L будет отцеплена первая группа вагонов, находящихся в хвосте состава, затем он переедет на другой путь, где будут отцеплены оставшиеся вагоны, находящиеся в начале состава, после чего локомотив вернется на первый путь за первой группой вагонов, а затем на второй – за второй. Таким образом, данная операция фактически осуществит разбивку прицепленных к локомотиву вагонов на две группы и переставит их местами. Формально эта операция может быть записана в виде следующего продукционного правила:

.                                          (4.1)

В этой записи символы обозначают произвольные подстроки из алфавита {A, B, C, D}, может быть и пустые.

Очевидно, что для состава, содержащего n вагонов, существует  различных вариантов применения продукционного правила (4.1), а следовательно, столько же различных состояний, в которые может перейти система после первого маневра. В результате применения продукции (4.1) к показанной на рисунке 3.6 ситуации система может перейти из начального состояния ABCD в следующие  три состояния BCDA, CDAB, DABC. Применяя продукцию (4.1) к состояниям, полученным на первом шаге, замечаем, что данное правило уже не способно генерировать новых состояний. Это означает, что продукционная система, основанная на единственном продукционном правиле, описываемом выражением (4.1), не является полной, то есть достаточной для решения задачи о маневрировании в общем случае.

Для решения задачи о маневрировании в общем случае, то есть получения любой перестановки вагонов из начального состояния, необходимо использовать более сложные маневры. Одним из них является отцеп части вагонов    на одном из путей и последующее маневрирование с использованием правила (4.1). Система продукций, описывающих процесс отцепа части вагонов, имеет вид:

                             (4.2)

,                                  (4.3)

где символы  так же, как и ранее, обозначают произвольные подстроки из  алфавита {A,B,C,D}, может быть и пустые.

Не трудно проверить, что, добавив к продукционному правилу (4.1) правила (4.2) и (4.3), получаем полную продукционную систему, на основе которой возможно решение задачи о маневрировании в общем случае.

Этап 3 В качестве механизма поиска решений выберем механизм прямого вывода. Его реализация сводится к итерационной процедуре генерации множества допустимых состояний на i-м шаге путем применения продукционных правил (4.1)–(4.3) к состояниям, сгенерированным на предыдущем (i-1)-м шаге. В качестве начального состояния рассматривается  исходный порядок расположения вагонов в составе ABCD.

Этап 4 Запускаем механизм вывода путем применения продукционного правила (4.2) к исходному состоянию ABCD. В результате получаем множество состояний, среди которых имеется состояние . Применяя к данному состоянию правило (4.1), получаем состояние . Применяя к полученному состоянию правило (4.3), получим искомое состояние BACD, описывающее требуемый порядок размещения вагонов в отцепе.

Задание

Практическое задание включает три самостоятельных задачи, связанные с ранее рассмотренной модельной задачей о маневрировании локомотива. Продукционная система для многошагового принятия решений содержит единственное правило, описывающее технологический маневр, в результате которого состав вагонов разбивается на три группы, первая группа вагонов, находящаяся в начале состава (ближе к локомотиву), маневром не затрагивается, а вторая и третья группы вагонов меняются местами. Формальным выражением, описывающим данный маневр, является следующее продукционное правило:

,                                          (4.4)

где символы , так же как и ранее, обозначают произвольные подстроки из  алфавита {A, B, C, D, E, F, G}, может быть и пустые.

 Задача 1. С использованием продукционного правила (4.4) и механизма прямого вывода требуется найти оптимальный план маневровых передвижений локомотива, позволяющий состав из 7 вагонов, находящихся в порядке ABCDEFG на пути П1, переставить в порядке DEBCFGA на путь П2. Критерием оптимальности является минимум числа маневров.

Задача 2. С использованием продукционного правила (4.4) и механизма обратного вывода требуется найти оптимальный план маневровых передвижений локомотива, позволяющий состав из 7 вагонов, находящихся в порядке ABCDEFG на пути П1, переставить в порядке CADEFGB на путь П2.

Задача 3. Обозначим через  вектор, состоящий из n символов, описывающий некоторый начальный порядок расположения вагонов в составе, подлежащем маневрированию. Пусть I, J – индексы, характеризующие границы разбиения вектора V на три группы элементов (I, J = o,1,…, n-1). Требуется составить и отладить на языке программирования MATLAB программу, которая, будучи примененная к вектору V, имитирует процесс реализации продукционного правила (4.4) при условии

.

Задача 4. Составить блок-схему алгоритма и программу на языке MATLAB для нахождения оптимального плана маневровых передвижений локомотива, позволяющую состав из n вагонов, начальный порядок которых задается вектором , пересортировать в порядке  с использованием минимального числа маневров. В качестве продукционного правила использовать формулу (4.4), а в качестве механизма вывода – механизм прямого вывода.