Лабораторная работа 3.10. Задачи оптимизации

Лабораторная работа 3.10. Задачи оптимизации

Задачи оптимизации отражают суть многих управленческих ситуаций. В этих задачах необходимо оптимизировать целевую функцию (показатель эффективности) для допустимых значений переменных решений. Возможные значения переменных задаются множеством ограничений в виде неравенств. Таким образом, необходимо выбрать значения переменных задачи в соответствии с ограничениями и при этом сделать целевую функцию наибольшей (задача максимизации) или наименьшей (задача минимизации). Например, в качестве целевой функции могут выступать прибыль, которую необходимо максимизировать, или затраты, подлежащие минимизации. Переменные, от которых зависит эта функция (например, количество продукции), должны удовлетворять каким-либо ограничениям (например, количество продукции не может быть отрицательным, затраты ресурсов не должны превосходить имеющихся запасов и т.д.).

Для решения такого рода задач Excel содержит средство Поиск решения. Этот инструмент помогает найти значения переменных, которые максимизируют или минимизируют значение в целевой ячейке. Он также позволяет задать ограничения - условия, которые должны выполняться при поиске решения.

Команда Поиск решения находится в меню Сервис. Если эта команда отсутствует в меню Сервис, то выберите пункт Надстройки и затем укажите Поиск решения в списке надстроек.

Рассмотрим использование средства Поиск решения на примере задачи планирования перевозок пассажиров и транспортной задачи.

1 Задача о планировании перевозок пассажиров состоит в следующем. Между двумя городами установлено железнодорожное сообщение, при этом перевозка пассажиров осуществляется пассажирскими и скорыми поездами. Каждый из видов поездов имеет в своем составе определенное число вагонов различного типа: багажный, почтовый, плацкартный, купейный, мягкий. Известно количество пассажиров, перевозимых в каждом из типов вагонов, а также общее число вагонов каждого типа на станции формирования поездов (табл. 3.6).

Таблица 3.6

Исходные данные о планировании перевозок пассажиров

Требуется определить оптимальное число скорых и пассажирских поездов, при которых общее число перевозимых пассажиров будет максимальным.

Выполнение:

1.1 Для решения этой задачи необходимо построить ее математическую модель. Процесс построения модели начинается с ответа на следующие три вопроса:

1) Для определения каких величин строится модель (т.е. каковы переменные модели)?

2) В чем состоит цель, для достижения которой из множества всех допустимых значений выбираются оптимальные?

3) Каким ограничениям должны удовлетворять неизвестные?

В нашей задаче переменными являются:

 - количество сформированных скорых поездов,

 - количество сформированных пассажирских поездов.

В одном скором поезде может быть перевезено  пассажира, соответственно, в одном пассажирском поезде может быть перевезено  пассажиров.

Общее число перевозимых пассажиров будет равно . Целью является определение среди всех допустимых значений  и  таких, которые максимизируют число перевозимых пассажиров, т.е. целевую функцию .

Тогда математическая постановка рассматриваемой задачи может быть записана в следующем виде:

                                                                      (3.1)

при выполнении ограничений:

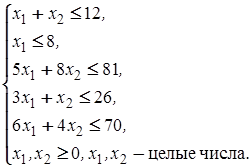                                                             (3.2)

Каждое из этих ограничений соответствует отдельным типам вагонов в составах скорых и пассажирских поездов.

1.2 Для решения задачи о планировании перевозок пассажиров с помощью программы Excel создайте новый лист Задача о поездах в книге Лабораторные.xls.

1.3 Внесите необходимые надписи в ячейки A1:D1, A2:A9, B4, D4, E4. Следует отметить, что конкретное содержание этих надписей не оказывает никакого влияния на решение рассматриваемой задачи.

1.4 В ячейки В3:С3 введите значения коэффициентов целевой функции: , .

1.5 В ячейку D2 введите формулу: =СУММПРОИЗВ(В2:С2 ; В3:С3), которая представляет собой целевую функцию (3.1).

1.6 В ячейки В5:С9 введите значения коэффициентов левых частей первых пяти ограничений (3.2), взятых из исходной таблицы (табл. 3.6).

1.7 В ячейки Е5:Е9 введите значения правых частей первых пяти ограничений (3.2), также взятых из исходной таблицы (табл. 3.6).

1.8 В ячейку D5 введите формулу: = СУММПРОИЗВ($В$2:$С$2 ; В5:С5), которая представляет собой левую часть первого ограничения (3.2).

1.9 Скопируйте формулу из ячейки D5 в ячейки D6:D9.

Таким образом, рабочий лист Excel с исходными данными для решения задачи примет вид (рис. 3.51).

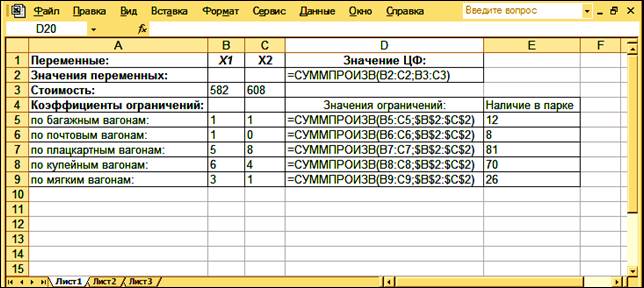
Рис. 3.51. Исходные данные для решения задачи о планировании перевозок   пассажиров

1.10 Для дальнейшего решения задачи следует вызвать мастер поиска решения: меню Сервис / Поиск решения.

1.11 Диалоговое окно Поиск решения заполните следующим образом:

- В поле с именем Установить целевую ячейку: введите абсолютный адрес ячейки $D$2 (или щелкните по ячейке D2, и ее адрес будет автоматически указан в данном поле).

- Для группы Равной: выберите вариант поиска решения - максимальному значению.

- В поле с именем Изменяя ячейки: введите абсолютный адрес ячеек $B$2 : $C$2 (для этого можно выделить этот диапазон на рабочем листе).

- Добавьте ограничения для рассматриваемой задачи. С этой целью выполните следующие действия:

• для задания первого ограничения в исходном диалоговом окне Поиск решения нажмите кнопку Добавить;

• в появившемся дополнительном окне в поле Ссылка на ячейку укажите диапазон $D$5:$D$9;

• в качестве знака ограничения из выпадающего списка выберите нестрогое неравенство « < = »;

• в качестве значения правой части ограничения выберите диапазон $E$5:$E$9;

• для добавления первого ограничения в дополнительном окне нажмите кнопку Добавить.

- Для внесения второго ограничения (на целочисленность) выполните следующие действия:

• в появившемся дополнительном окне в поле Ссылка на ячейку укажите диапазон $В$2:$С$2;

• в качестве знака ограничения из выпадающего списка выберите строку «цел»;

• в качестве значения правой части ограничения в поле с именем Ограничение: оставьте без изменения вставленное программой значение «целое»;

• в дополнительном окне нажмите кнопку ОК.

- В дополнительных параметрах мастера поиска решения (кнопка Параметры окна Поиск решения) выберите отметки Линейная модель и Неотрицательные значения.

Вид диалогового окна Поиск решения представлен на рис. 3.52.

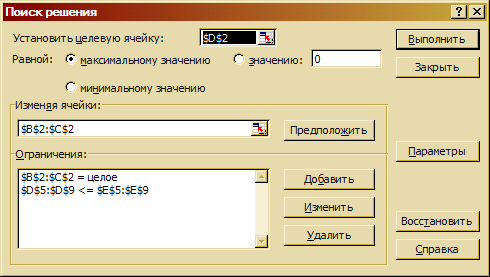
Рис. 3.52. Заполненное окно Поиск решения для задачи

о планировании перевозок пассажиров

- После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить.

После выполнения расчетов программой Excel будет получено решение, которое имеет следующий вид (рис. 3.53).

Рис. 3.53. Результат решения задачи о планировании перевозок пассажиров

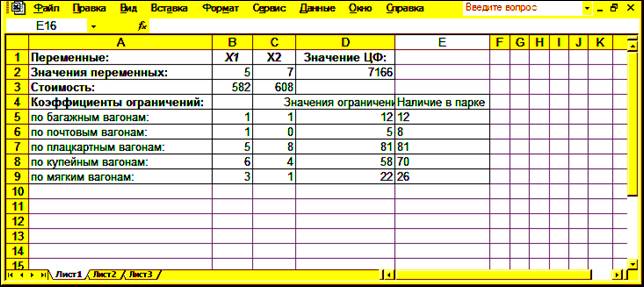
Таким образом, результатом решения задачи о планировании перевозок пассажиров являются найденные оптимальные значения переменных: , которым соответствует значение целевой функции: .

Анализ найденного решения показывает, что из имеющегося парка вагонов для обеспечения максимального количества перевезенных пассажиров следует составить 5 скорых и 7 пассажирских поездов. При этом имеющиеся в парке багажные и плацкартные вагоны будут полностью использованы для формирования поездов, а 3 почтовых, 12 купейных и 4 мягких вагона из парка останутся неиспользованными в этих поездах.

2 Классическая транспортная задача формулируется следующим образом. В  пунктах производства  имеется однородный груз в количестве соответственно . Этот груз необходимо доставить в  пунктов назначения  в количестве соответственно . Стоимость перевозки единицы груза (тариф) из пункта  в пункт  равна . Требуется составить план перевозок, позволяющий вывезти все грузы и имеющий минимальную стоимость.

R Если суммарные запасы груза равны суммарным потребностям в нем 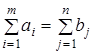, то задача называется закрытой. Если 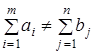, то открытой.

Для решения этой задачи необходимо построить ее математическую модель. Неизвестными в данной задаче являются объемы перевозок. Пусть  - объем перевозок из пункта производства  в пункт назначения . Целевая функция - это суммарные транспортные расходы, т.е. .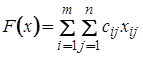

Неизвестные в данной задаче должны удовлетворять следующим ограничениям:

- объемы перевозок не могут быть отрицательными;

- вся продукция должна быть вывезена из пунктов производства, а потребности всех пунктов назначения должны быть полностью удовлетворены.

В результате получим следующую модель:

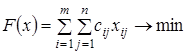
при ограничениях

,                                                                                          

,                                                                                          

,   ,  .                                                                   

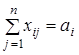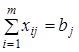Оптимальным решением задачи будет являться матрица , удовлетворяющая системе ограничений и доставляющая минимум целевой функции.

Рассмотрим пример транспортной задачи. Пусть имеются 3 пункта производства () и 4 пункта назначения (). Данные о наличии груза в пунктах производства, потребностях пунктов назначения и стоимости перевозки единицы груза из пункта  в пункт  приведены в таблице (табл. 3.7).

Таблица 3.7

Исходные данные транспортной задачи

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

Выполнение:

2.1 Для решения задачи с помощью программы Excel создайте новый лист Трансп_задача в книге Лабораторные.xls.

2.2 Введите данные, как показано на рис. 3.54.

2.3 В ячейки В2:Е4 введите стоимости перевозок. В ячейки F2:F4 введите объемы производства, а в ячейки В5:Е5 - потребности в грузе в пунктах назначения. Ячейки В8:Е10 отведите под значения неизвестных (объемы перевозок). В ячейку F12 введите формулу для расчета целевой функции: =СУММПРОИЗВ(В2:Е4;В8:Е10).

Рис. 3.54. Исходные данные транспортной задачи

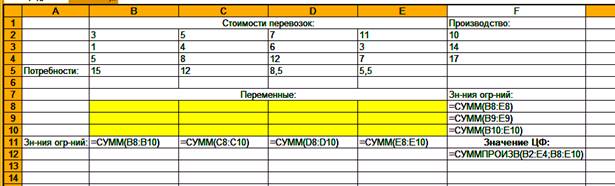
2.4 В ячейку В11 введите формулу: =СУММ(В8:В10). Скопируйте эту формулу из ячейки В11 в ячейки С11:Е11.

Значения в ячейках В11:Е11 определяют объемы груза, ввозимого в пункты назначения.

2.5 В ячейку F8 введите формулу: =СУММ(В8:Е8). Скопируйте эту формулу в ячейки F9:F10.

Формулы в ячейках F8:F10 вычисляют объем груза, вывозимого из пунктов производства.

2.6 Выберите команду Сервис / Поиск решения. Заполните открывшееся диалоговое окно, как показано на рис. 3.55.

Рис. 3.55. Заполненное окно Поиск решения для транспортной задачи

2.7 В диалоговом окне Параметры поиска решения установите флажок Линейная модель. После нажатия кнопки Выполнить средство поиска решений находит оптимальный план перевозки грузов и соответствующие ему транспортные расходы (рис. 3.56).

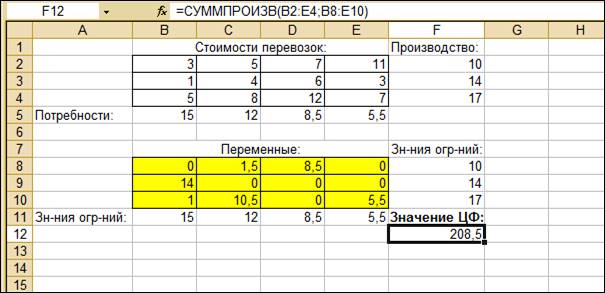
Рис. 3.56. Результат решения транспортной задачи

3 Решите транспортную задачу, исходные данные для которой выберите по варианту (номер варианта соответствует последней цифре номера зачётной книжки).

Варианты