
Лабораторная работа 3.5. Графики функций и поверхности
1 Откройте рабочую книгу Лабораторные.xls. Вставьте новый
лист График 1. Постройте на этом листе график функции y=cos(x) при ![]() .
.
Выполнение:
1.1 Сначала необходимо построить таблицу значений функции при различных значениях аргумента, который изменяется с фиксированным шагом. Столбец А будет содержать значения х, а столбец В - значения y.
1.2 Введите в ячейку А1 формулу =-ПИ(), в ячейку А20 формулу =ПИ().
1.3 Выделите диапазон А1:А20 и выберите меню Правка / Заполнить / Прогрессия (рис. 3.22). Выберите автоматическое определение шага и нажмите ОК.
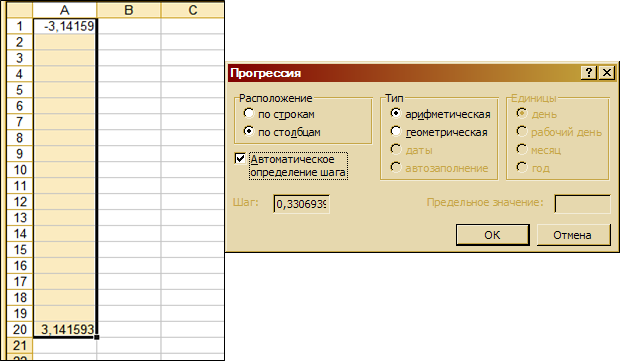 |
Рис. 3.22. Заполнение столбца А значениями аргумента
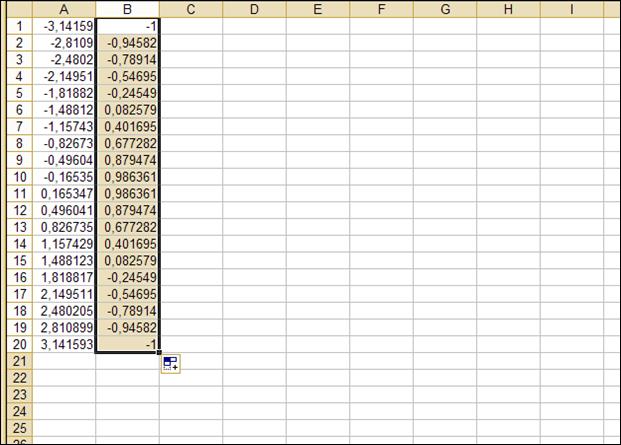
1.4 Далее необходимо в диапазон В1:В20 ввести значения функции. Для этого в ячейку В1 внесите формулу =COS(A1). Эту формулу «протащите» на весь диапазон В1:В20.
1.5 Выделите диапазон В1:В20, вызовите мастер диаграмм. На первом шаге мастера выберите вкладку Нестандартные, тип Гладкие графики. Нажмите Готово (рис. 3.23).
2 Постройте график функции y(x) при ![]() :
: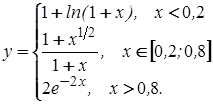 .
.
Выполнение:
2.1 В рабочую книгу Лабораторные.xls вставьте новый лист График 2. В столбец А будем заносить значения аргумента х, который также изменяется с фиксированным шагом. Его значение целесообразно сделать небольшим. В нашем случае будем считать, что шаг изменения аргумента равен 0,1.
2.2 В ячейку А1 введите первое значение аргумента х: 0.
 |
2.3 В ячейку А2 введите второе значение х: 0,1 - первое значение, увеличенное на величину шага: 0 + 0,1 = 0,1 (рис. 3.24).
2.4 Выделите обе ячейки А1:А2, подведите курсор мыши к правому нижнему углу выделенного диапазона, курсор примет знак черного крестика; «протащите» черный крестик вниз, пока значение в ячейке не станет равным 1 (ячейка А11).
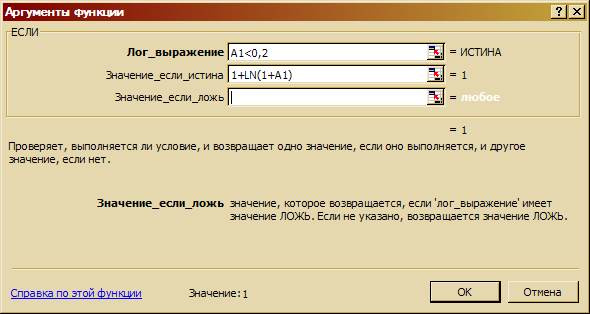
2.5 Введите значения функции в столбец В: в ячейку В1 поставьте знак «равно» и вызовите функцию ЕСЛИ. В открывшемся окне Аргументы функции в поле Лог_выражение введите А1<0,2, в поле Значение_если истина - 1+LN(1+A1) (рис. 3.25). Поставьте курсор в поле Значение_если ложь и еще раз войдите в функцию ЕСЛИ.
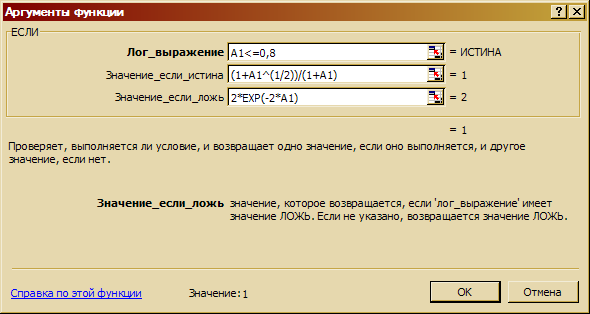
2.6 В открывшемся окне новой функции ЕСЛИ, которая будет вложена в предыдущую, в поле Лог_выражение введите А1<=0,8, в поле Значение_если истина - (1+А1^(1/2))/(1+A1), в поле Значение_если ложь - 2*EXP(-2*A1) (рис. 3.26). Нажмите ОК.
2.7 «Протащите» за маркер автозаполнения получившуюся формулу =ЕСЛИ(A1<0,2;1+LN(1+A1);ЕСЛИ(A1<=0,8;(1+A1^(1/2))/(1+A1);2*EXP(‑2*A1))) до ячейки В11.
2.8 Выделите диапазон В1:В11 и вызовите мастер диаграмм. Выберите тип диаграммы График, щелкните по нужному образцу. Нажмите Далее.
2.9 Перейдите на вкладку Ряд. Войдите в поле Подписи оси Х и выделите мышью на рабочем листе диапазон А1:А11 (то есть весь столбец значений х). Нажмите Далее.
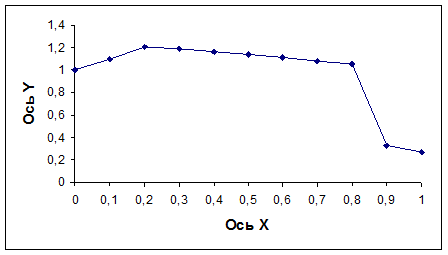
2.10 При настройке параметров диаграммы укажите заголовки осей (Ось Х и Ось Y), удалите легенду и линии сетки.
2.11 Разместите график на имеющемся листе. В области построения диаграммы установите невидимую рамку и прозрачную заливку.
2.12 Выполните двойной щелчок мышью на оси Х диаграммы (оси категорий), в появившемся диалоговом окне Формат оси перейдите на вкладку Шкала, снимите флажок Пересечение с осью Y (значений) между категориями. Это позволит разместить подписи на оси Х под делениями. Нажмите ОК.
График примет вид (рис. 3.27).
3 Постройте графики функций:
а)
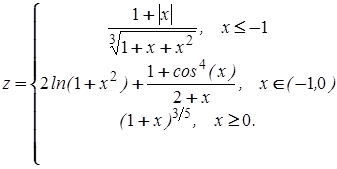 при
при ![]() .
.
б) 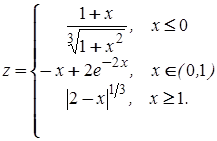 при
при ![]() .
.
в) 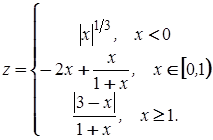 при
при ![]() .
.
Указания:
• При написании формул используйте следующие правила записи функций (табл. 3.6); всегда ставьте знаки умножения.
Примеры функций
|
|
ABS(x) |
|
|
x^(1/n) |
|
|
(cos(x))^ m |
|
ex |
EXP(x) |
4 Постройте поверхность z = x2 – y2 при ![]() .
.
Выполнение:
4.1 В книгу Лабораторные.xls вставьте новый лист Поверхности.
4.2 В диапазон ячеек B1:L1 введите последовательность значений: ‑1; ‑0,8;…;1 переменной у, а в диапазон ячеек А2:А12 – последовательность значений: -1; -0,8; …; 1 переменной х.
4.3 В ячейку В2 введите формулу =$A2^2-B$1^2. Выделите эту ячейку, установите указатель мыши на ее маркере заполнения и «протащите» его так, чтобы заполнить весь диапазон B2:L12.
При работе с формулой в ячейке В2 использовались смешанные ссылки. Если знак $ поставить перед именем столбца ($A2), то фиксируется этот столбец (А); если перед номером строки (B$1), то фиксируется вся эта строка и при копировании формула будет ссылаться на ячейки в этой строке (в нашем случае в строке 1).
4.4 Выделите диапазон ячеек А1:L12, содержащий таблицу значений функции и ее аргументов, и вызовите мастер диаграмм. Выберите тип диаграммы – Поверхность. В итоге поверхность примет вид (рис. 3.28).
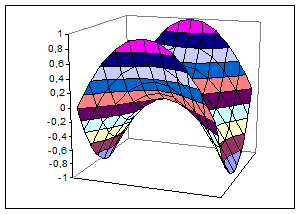
5 Постройте поверхности:
а) ![]() при
при
![]() .
.
б) ![]() при
при
![]() .
.
с) ![]() при
при
![]() .
.
6 Найдите корни уравнения: х3 – 0,01х2 – 0,7044х + 0,139104 = 0.
Выполнение:
6.1 В рабочую книгу вставьте новый лист Корни уравнения.
6.2 Вещественных корней у полинома третьей
степени может быть не более трех, необходимо их локализовать. Для этого
постройте график функции, где аргумент изменяется, например, на отрезке ![]() с шагом 0,2. Запишите в ячейку А1
слово х, в В1 - слово y. Заполните
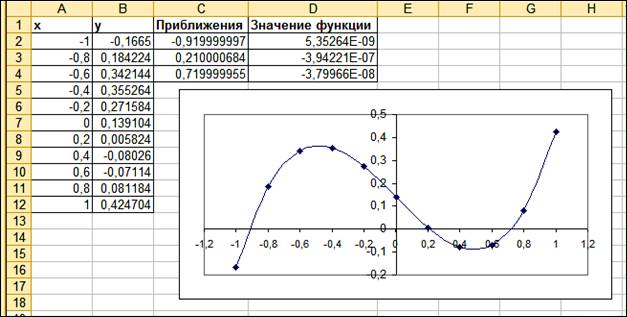
диапазон А2:А12 значениями х, в ячейку В2 введите формулу =А2^3-0,01*A2^2-0,7044*A2+0,139104 и протяните вниз
до В12. Постройте график полученной функции. Из него видно, что полином меняет
знак на интервалах (-1;-0,8), (0,2;0,4), (0,6;0,8). Значит, корни находятся в
этих интервалах. Введите также заголовки: в ячейку С1 - слово Приближения, в D1 - Значение функции.
с шагом 0,2. Запишите в ячейку А1
слово х, в В1 - слово y. Заполните
диапазон А2:А12 значениями х, в ячейку В2 введите формулу =А2^3-0,01*A2^2-0,7044*A2+0,139104 и протяните вниз
до В12. Постройте график полученной функции. Из него видно, что полином меняет
знак на интервалах (-1;-0,8), (0,2;0,4), (0,6;0,8). Значит, корни находятся в
этих интервалах. Введите также заголовки: в ячейку С1 - слово Приближения, в D1 - Значение функции.
6.3 Войдите в меню Сервис / Параметры / Вычисления, задайте предельное число итераций и относительную погрешность (1000 и 0,00001).
6.4 В качестве начальных значений (приближенных) корней задают любые точки из отрезков локализации корней. Например, возьмите -0,9 (из первого интервала), 0,3 (из второго) и 0,7 (из третьего). Введите их в С2:С4.
6.5 Для вычисления значений функции, соответствующих приближенным решениям, в ячейку D2 введите следующую формулу: =C2^3‑0,01*C2^2‑0,7044*C2+0,139104. Протяните эту формулу вниз на D2:D4.
6.6 Таким образом, получены три пары значений «приближенный корень – уравнение для него» в ячейках C2:D2, C3:D3, C4:D4. Для каждой из этих пар примените функцию Excel Сервис / Подбор параметра, которая позволяет по известному результату (значение уравнения равно нулю) подобрать неизвестное значение параметра (здесь - аргумента х, корня). Начните с первой пары:
- вызовите меню Сервис / Подбор параметра, в окне заполните:
Установить в ячейке: $D$2 (где формула с вычислением левой части уравнения);
Значение: 0 (значение правой части уравнения);
Изменяя значение ячейки: $C$2 (где искомый аргумент х).
Нажмите кнопку ОК.
Результат (значение первого корня) появится в ячейке С2. Аналогичную процедуру проделайте для каждой из оставшихся пар. В итоге в ячейках С2, С3 и С4 появятся значения всех корней (рис. 3.29).
7 Найдите корни уравнения 0,3х3 – 0,8756х2 + 0,0021х – 0,44 = 0.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.