Лабораторная работа по информатике и ИКТ

ЛАБОРАТОРНАЯ РАБОТА №3 РАБОТА С ПАКЕТОМ MATHCAD. ОСНОВНЫЕ ВОЗМОЖНОСТИ

ЦЕЛЬ РАБОТЫ

Познакомится с возможностями пакета MathCAD.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

К          основным элементам математических выражений MathCAD относятся типы данных, операторы, функции и управляющие структуры.

ОПЕРАТОРЫ

Операторы - элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д.

Оператор определяет:

1.     действие, которое должно выполняться при наличии тех или иных значений операндов;

2.     сколько, где и какие операнды должны быть введены в оператор.

Операнд – число или выражение, на которое действует оператор. Например, в выражении 5! + 3 число 3 и выражение 5! – операнды оператора

+   (плюс), а число 5 операнд оператора факториал (!). После указания операндов операторы становятся исполняемыми по документу блоками.

ТИПЫ ДАННЫХ

К   типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы) и данные файлового типа.

Константами называют поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т. д. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы в MathCAD представляют собой набор латинских или греческих букв и цифр.

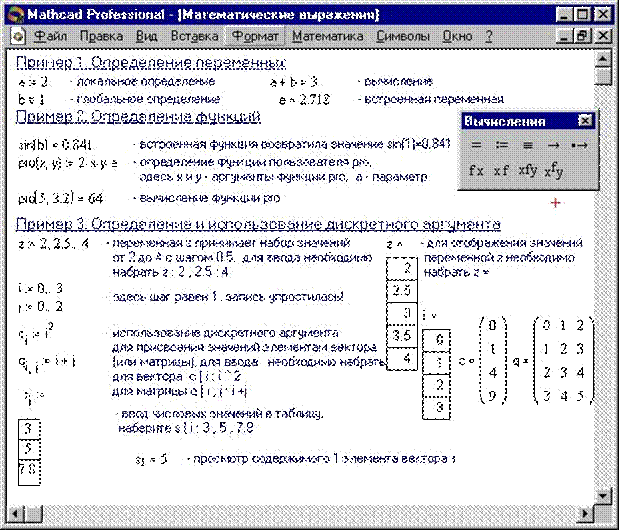
В    MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные системой начальные значения. Изменение значений системных переменных

производят во вкладке Встроенные переменные диалогового окна Math Options команды Математика Þ Опции.

Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной.

Если переменной присваивается начальное значение с помощью оператора :=, вызывается нажатием клавиши : (двоеточие) на клавиатуре, такое присваивание называется локальным. До этого присваивания переменная не определена и ее нельзя использовать. Однако с помощью

знака º (клавиша ~ на клавиатуре) можно обеспечить глобальное присваивание. MathCAD прочитывает весь документ дважды слева направо и сверху вниз. При первом проходе выполняются все действия, предписанные локальным оператором присваивания (º), а при втором – производятся действия, предписанные локальным оператором присваивания (:=), и отображаются все необходимые результаты вычислений (=).

Существуют также жирный знак равенства = (комбинация клавиш Ctrl + =), который используется, например, как оператор приближенного равенства при решении систем уравнений, и символьный знак равенства ® (комбинация клавиш Ctrl + .).

Дискретные аргументы – особый класс переменных, который в пакете MathCAD зачастую заменяет управляющие структуры, называемые циклами (однако полноценной такая замена не является). Эти переменные имеют ряд фиксированных значений, либо целочисленных (1 способ), либо в виде чисел с определенным шагом, меняющихся от начального значения до конечного (2 способ).

1. Name := Nbegin .. Nend,

где Name – имя переменной, Nbegin – ее начальное значение, Nend – конечное значение, .. – символ, указывающий на изменение переменной в заданных пределах (вводится клавишей ;). Если Nbegin < Nend, то шаг переменной будет равен +1, иначе –1.

2. Name := Nbegin, (Nbegin + Step) .. Nend

Здесь Step – заданный шаг изменения переменной (он должен быть положительным, если Nbegin < Nend, или отрицательным в обратном случае).

Дискретные аргументы значительно расширяют возможности MathCAD, позволяя выполнять многократные вычисления или циклы с повторяющимися вычислениями, формировать векторы и матрицы

Массив – имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов:

·        одномерные (векторы);

·        двумерные (матрицы).

Порядковый  номер  элемента,  который  является  его  адресом,

называется индексом. Индексы могут иметь только целочисленные значения. Они могут начинаться с нуля или единицы, в соответствии со значением системной переменной ORIGIN.

Векторы и матрицы можно задавать различными способами:

·        с помощью команды Вставка Þ Матрица, или комбинации клавиш

·        + M, или щелчком на кнопке  панели Матрица, заполнив массив пустых полей для не слишком больших массивов;

·        с использованием дискретного аргумента, когда имеется некоторая явная зависимость для вычисления элементов через их индексы.

ФУНКЦИИ

Функция –  выражение,  согласно  которому  проводятся  некоторые

вычисления с аргументами и определяется его числовое значение.

Следует особо отметить разницу между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются

ее     аргументами и заменяются при вычислении функции значениями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции.

Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение.

Функции в пакете MathCAD могут быть встроенные , т. е. заблаговременно введенные разработчиками, и определенные пользователем.

Способы вставки встроенной функции:

1.     Выбрать пункт меню Вставка Þ Функция.

2.     Нажать комбинацию клавиш Ctrl + E.

3.     Щелкнуть на кнопке .

ТЕКСТОВЫЕ ФРАГМЕНТЫ Текстовые фрагменты представляют собой куски текста, которые

пользователь хотел бы видеть в своем документе. Существуют два вида текстовых фрагментов:

·        текстовая область предназначена для небольших кусков текста -

подписей, комментариев и т. п. Вставляется с помощью команды Вставка Þ Текстовая регион или комбинации клавиш Shift + "

(двойная кавычка);

·        текстовый абзац применяется в том случае, если необходимо работать с абзацами или страницами. Вставляется с помощью комбинации клавиш Shift + Enter.

ГРАФИЧЕСКИЕ ОБЛАСТИ

Графические области делятся на три основных типа - двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим MathCAD на основании обработанных данных.

Для создания декартового графика:

1.                 Установить визир в пустом месте рабочего документа.

2.                 Выбрать команду Вставка Þ График Þ Х-У график, или нажать комбинацию клавиш Shift + @, или щелкнуть кнопку  панели Графики. Появится шаблон декартового графика.

3.                 Введите в средней метке под осью Х первую независимую переменную, через запятую – вторую и так до 10, например х1, х2, …

4.                 Введите в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую – вторую и т. д., например у1(х1), у2(х2), …, или соответствующие выражения.

5.                 Щелкните за пределами области графика, что бы начать его построение.

Трехмерные, или 3D-графики, отображают функции двух переменных вида Z(X, Y).

ЗАДАНИЕ

Упражнение 1.

Вычислить:

Это и все остальные задания снабдить команду Вставка Þ Текстовая область.

10! =

комментариями, используя

Вычислить выражения.

С    помощью команды ФорматÞРезультатÞФормат чиселÞЧисло знаков изменить точность отображения результатов вычисления глобально.

Упражнение 3.

Вывести на экран значение системной константы p и установить максимальный формат ее отображения локально.

Упражнение 4.

Выполнить следующие операции с комплексными числами:

=−3+2 

Выполнить следующие операции:

i = 1 .. 5

åi =

i

Õ   (i

i

+ 1)

=

x := 2

Упражнение 6.

Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции S(d) и R(d), используя команду

ВставкаÞГрафикÞX-Y Зависимость.

Упражнение 7.

Построить декартовые (X-Y Зависимость) и полярные (Полярные Координаты) графики следующих функций:

  (  ) = cos(  ) ∙       (  ),

  (  ) = 1.5      (  )² − 1,

  (  ) =       (  ).

Для этого необходимо определить a как дискретный аргумент на интервале от 0 до 2×p с шагом p/30.

Упражнение 8.

Используя команду ВставкаÞМатрица создать матрицу Q размером 6´6, заполнить ее произвольно и отобразить графически с помощью команды ВставкаÞГрафикÞПоверхности.

Упражнение 9.

Построить график поверхности (Поверхности) и карту линий уровня

(Контурный) для функции двух переменных

  (  ,   ) =  ∙       (  ) ∙       (  )

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.                 С помощью какого оператора можно вычислить выражение?

2.                 Как вставить текстовую область в документ Mathcad?

3.                 Чем отличается глобальное и локальное определение переменных? С помощью каких операторов определяются?

4.                 Как изменить формат чисел для всего документа?

5.                 Как изменить формат чисел для отдельного выражения?

6.                 Какие системные (предопределенные) переменные Вам известны? Как узнать их значение? Как изменить их значение?

7.                 Какие виды функций в Mathcad Вам известны?

8.                 Как вставить встроенную функцию в документ Mathcad?

9.                 С помощью каких операторов можно вычислить интегралы, производные, суммы и произведения?

10.            Как определить дискретные переменные с произвольным шагом? Какой шаг по умолчанию?

11.            Как определить индексированную переменную?

12.            Какие виды массивов в Mathcad Вам известны?

13.            Какая системная переменная определяет нижнюю границу индексации элементов массива?

14.            Опишите способы создания массивов в Mathcad.

15.            Как просмотреть содержимое массива, определенного через дискретный аргумент?

16.            Как построить графики: поверхности; полярный; декартовый?

17.            Как построить несколько графиков в одной системе координат?

18.            Как изменить масштаб графика?

19.            Как определить координату точки на графике?

20.            Как построить гистограмму?

21.            Какие функции используются для построения трехмерных графиков?