Лабораторная работа "Определение заряда, ёмкости и энергии конденсатора! 10 класс

Лабораторная работа № 25 Тема: Определение заряда, ёмкости и энергии конденсатора Цель: научиться экспериментальным путём находить характеристики конденсатора Оборудование: макетная плата, оксидный конденсатор ёмкостью 1000­2000 мкФ (можно составить батарею из нескольких параллельно соединённых меньшей ёмкости), секундомер, микроамперметр на 100 мкА или авометр, вольтметр, резистор 10 кОм, переменный резистор 500 кОм, ключ, источник питания на 4­6 В, соединительные провода Краткая теория Пот   подключении   конденсатора   к   источнику   постоянного   тока   его обкладки заряжаются равными по величине, но противоположными по знаку зарядами. 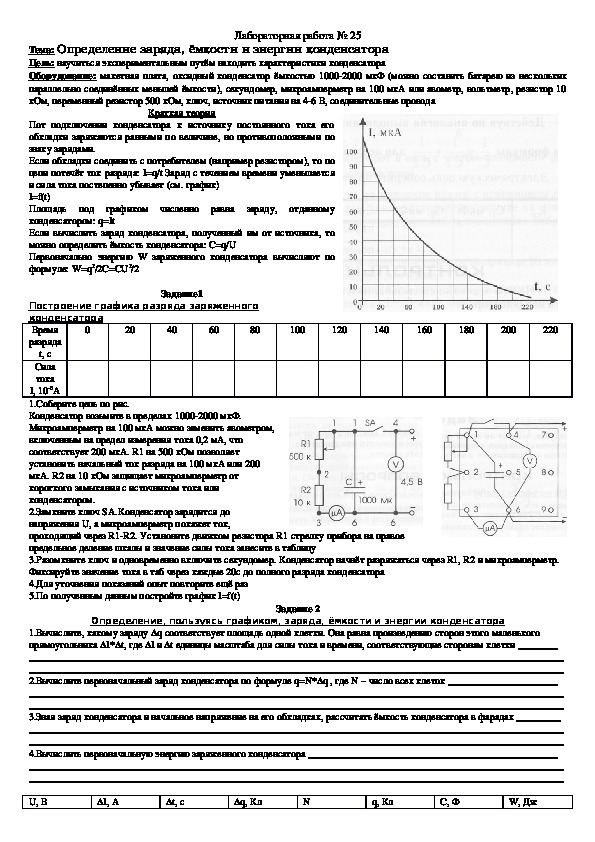Если обкладки соединить с потребителем (например резистором), то по цепи потечёт ток разряда: I=q/t Заряд с течением времени уменьшается и сила тока постепенно убывает (см. график) I=f(t) Площадь   под   графиком   численно   равна   заряду,   отданному конденсатором: q=It Если вычислить заряд конденсатора, полученный им от источника, то можно определить ёмкость конденсатора: С=q/U Первоначально   энергию  W  заряженного   конденсатора   вычисляют   по формуле: W=q2/2C=CU2/2 Задание1 Построение графика разряда заряженного конденсатора Время разряда 40 60 0 20 80 100 120 140 160 180 200 220 t, c Сила тока I, 10­6А 1.Соберите цепь по рис. Конденсатор возьмите в пределах 1000­2000 мкФ. Микроамперметр на 100 мкА можно заменить авометром, включенным на предел измерения тока 0,2 мА, что соответствует 200 мкА. R1 на 500 кОм позволяет установить начальный ток разряда на 100 мкА или 200 мкА. R2 на 10 кОм защищает микроамперметр от короткого замыкания с источником тока или конденсатором. 2.Замкните ключ SA.Конденсатор зарядится до напряжения U, а микроамперметр покажет ток, проходящий через R1­R2. Установите движком резистора R1 стрелку прибора на правое предельное деление шкалы и значение силы тока занесите в таблицу 3.Разомкните ключ и одновременно включите секундомер. Конденсатор начнёт разряжаться через R1, R2 и микроамперметр.  Фиксируйте значение тока в таб через каждые 20с до полного разряда конденсатора 4.Для уточнения показаний опыт повторите ещё раз 5.По полученным данным постройте график I=f(t) Задание 2 Определение, пользуясь графиком, заряда, ёмкости и энергии конденсатора 1.Вычислите, какому заряду Δq соответствует площадь одной клетки. Она равна произведению сторон этого маленького  прямоугольника ΔI*Δt, где ΔI и Δt единицы масштаба для силы тока и времени, соответствующие сторонам клетки ________ ___________________________________________________________________________________________________________ ___________________________________________________________________________________________________________ 2.Вычислите первоначальный заряд конденсатора по формуле q=N*Δq , где N – число всех клеток ______________________ ___________________________________________________________________________________________________________ ___________________________________________________________________________________________________________ 3.Зная заряд конденсатора и начальное напряжение на его обкладках, рассчитать ёмкость конденсатора в фарадах _________ ___________________________________________________________________________________________________________ ___________________________________________________________________________________________________________ 4.Вычислить первоначальную энергию заряженного конденсатора __________________________________________________ ___________________________________________________________________________________________________________ ___________________________________________________________________________________________________________ U, В ΔI, А Δt, с Δq, Кл N q, Кл C, Ф W, Дж