Добавить материал

и получить 10 документов
и свидетельство СМИ

Кублик Галина Евгеньевна

Методические рекомендации к практическим занятиям по дисциплине ЕН.01 Математика специальности 38.02.06 Финансы

Лабораторные работы
docx
22.12.2024

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Методические рекомендации к практическим занятиям по дисциплине ЕН.01 Математика специальности 38.02.06 Финансы

Метод. реком к практ занятиям финансисты.docx

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное

учреждение высшего образования

«Крымский федеральный университет имени В.И. Вернадского»

(ФГАОУ ВО «КФУ им. В.И. Вернадского»)

Ордена Трудового Красного Знамени агропромышленный колледж
имени Э.А. Верновского (филиал) ФГАОУ ВО «КФУ им. В.И.Вернадского»

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

ПО УЧЕБНОЙ ДИСЦИПЛИНЕ

ЕН.01 МАТЕМАТИКА

^{(номер
и название учебной дисциплины (МДК))}

Специальность: 38.02.06 Финансы

^{(номер
и название специальности)}

Маленькое, 2024 г.

Содержание

	стр.
Пояснительная записка	3
Перечень практических занятий	5
Инструкционные карты по практическим занятиям	6
Учебно-методическое обеспечение	47

Пояснительная записка

Цели и задачи учебной дисциплины – требования к результатам освоения дисциплины:

Результатом освоения учебной дисциплины является овладение обучающимися в соответствии с ФГОС по специальности 38.02.06 Финансы

следующими личностными (ЛР) результатами и общими компетенциями:

1. личностные (ЛР) результаты:

Код	Наименование результата обучения
ЛР 4	Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

2. общие (ОК) компетенции:

Код	Наименование результата обучения
ОК 01	Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам
ОК 02	Использовать современные средства поиска, анализа и интерпретации информации и информационные технологии для выполнения задач профессиональной деятельности.

В результате освоения учебной дисциплины обучающийся должен уметь:

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₃. Определять этапы решения задачи;

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₅. Составить план действия; определить необходимые ресурсы;

У₆. Владеть актуальными методами работы в профессиональной и смежных сферах;

У₇. Реализовать составленный план;

У₈. Оценивать результат и последствия своих действий (самостоятельно или с помощью наставника);

У₉. Определять задачи для поиска информации;

У₁₀. Определять необходимые источники информации;

У₁₁. Планировать процесс поиска;

У₁₂. Структурировать получаемую информацию;

У₁₃. Выделять наиболее значимое в перечне информации;

У₁₄. Оценивать практическую значимость результатов поиска;

У₁₅. Оформлять результаты поиска;

У₁₆. Применять средства информационных технологий для решения профессиональных задач;

У₁₇. Использовать современное программное обеспечение.

В результате освоения учебной дисциплины обучающийся должен знать:

З₁. Актуальный профессиональный и социальный контекст, в котором приходится работать и жить;

З₂. Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;

З₃. Алгоритмы выполнения работ в профессиональной и смежных областях;

З₄. Методы работы в профессиональной и смежных сферах;

З₅. Структуру плана для решения задач;

З₆. Порядок оценки результатов решения задач профессиональной деятельности;

З₇. Номенклатуру информационных источников применяемых в профессиональной деятельности;

З₈. Приемы структурирования информации;

З₉. Формат оформления результатов поиска информации;

З₁₀. Современные средства и устройства информатизации; порядок их применения и программное обеспечение в профессиональной деятельности.

Перечень практических занятий

№ п/п	Название и номер практического занятия	Кол-во часов
1, 2	Решение задач с комплексными числами. Геометрическая интерпретация комплексного числа	4
3	Действия над матрицами	2
4	Определители второго и третьего порядков	2
5	Решение матричных уравнений	2
6	Формулы Крамера (для систем линейных уравнений с тремя неизвестными)	2
7,8	Метод Гаусса (метод исключения неизвестных)	4
9	Экстремум функции нескольких переменных	2
10	Нахождение неопределённого интеграла, используя его свойства	2
11	Методы замены переменной и интегрирования по частям	2
12, 13	Правила замены переменной и интегрирования по частям	4
14, 15	Дифференциальные уравнения первого порядка и первой степени	4
16	Уравнения с разделяющимися переменными	2
17	Итоговая контрольная работа	2













	ИТОГО	34

Инструкционные карты к практическим занятиям

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1, 2

Тема: «Решение задач с комплексными числами. Геометрическая интерпретация комплексного числа».

Тема 1.1. Комплексные числа и действия над ними.

1. Определение комплексного числа в алгебраической форме, действия над ними.

2. Геометрическое изображение комплексных чисел.

3. Модуль и аргументы комплексного числа.

4. Решение алгебраических уравнений.

Цель занятия: научиться находить целую и мнимую части, модуль комплексного числа, выполнять арифметические операции с комплексными числами (сложение и вычитание, умножение и деление), а также возведение мнимой единицы в степень, решать квадратные уравнения в комплексных числах. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ЛР 4, У₄, У₅, У₇.

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₅. Составить план действия; определить необходимые ресурсы;

У₇. Реализовать составленный план.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Комплексные числа и действия над ними».

2. Выполнить тест № 1 по теме «Комплексные числа и действия над ними» в четырех вариантах, согласно своего номера в журнале.

3. Оформить задания в тетради для практических работ.

4. Выполнить задания по образцу совместно с преподавателем.

5. Выполнить индивидуальное задание по варианту в тетради для практических работ.

6. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

I. Теоретический опрос по теме «Комплексные числа и действия над ними».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Дайте определение мнимой единицы.

2. Как вычисляют степени мнимой единицы?

3. Какое число называется комплексным?

4. Какие комплексные числа называются чисто мнимыми? Приведите примеры комплексных чисел, чисто мнимых чисел.

5. Какие комплексные числа называются равными?

6. Какие комплексные числа называются сопряженными?

7. Как выполняются сложение, вычитание, умножение комплексных чисел в алгебраической форме?

8. Как выполняется деление комплексных чисел в алгебраической форме?

9. Как геометрически изображаются комплексные числа?

10. Что называется модулем и аргументом комплексного числа?

11. Напишите формулы для модуля и аргумента комплексного числа.

12. Формы комплексных чисел.

13. Какие корни и сколько корней имеет квадратное уравнение с отрицательным дискриминантом?

14. Как решить квадратное уравнение, если его дискриминант отрицателен?

Выполнить тест № 1 по теме «Комплексные числа и действия над ними».

Тест состоит из 10 вопросов в четырех вариантах, вариант выбрать, согласно своего номера в журнале. За 2 правильных ответа – 1 балл. Максимальное количество баллов – 5.

III. Выполнение заданий по образцу совместно с преподавателем.

Пример № 1. Выполнить действия с комплексными числами: :

1. Сложить два комплексных числа:

2. Найти разность двух комплексных чисел:

3. Найти произведение двух комплексных чисел:

4. Найти частное двух комплексных чисел:

5. Найти модуль комплексных чисел:

Пример № 2. Возвести в степень комплексные числа , ,

Пример № 3. Извлечь корень из комплексного числа:

Пример № 4. Решить квадратное уравнение:

Пример № 5. Построить на комплексной плоскости следующие комплексные числа:
, , ,, , , , , ,

Пример № 6: Представить в тригонометрической и показательной формах число .

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Действия над комплексными числами» в форме расчетно-графического задания по вариантам согласно своего номера в журнале.

Задание 1. Даны два комплексных числа и . Вычислите: . Построите геометрическую модель комплексных чисел и

1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Задание 2. Решите квадратные уравнения:

1 вариант

2 вариант

3 вариант

a) x²– 2x + 8 = 0;

b) x²– 4x + 5 = 0;

a) x²+ 6x + 25 =0;

b) x²-2x+2=0;

a) x²+ 6x + 69 = 0;

b) x²-4x +16 = 0;

Вопросы для закрепления.

1. Что такое главный аргумент комплексного числа?

2. Геометрическая интерпретация комплексного числа, множество комплексных чисел?

3. Какие правила действия над комплексными числами в алгебраической форме (сложение, вычитание, умножение, деление) вы знаете?

4. Как выглядит тригонометрическая форма комплексного числа?

5. Как выглядит показательная форма комплексного числа?

Литература: Электронный ресурс. О₃:Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440 - п. 15.1 – 15.2 стр.356.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3

Тема: «Действия над матрицами».

Тема 2.1. Матрицы и определители.

1. Матричные модели. Определение матрицы.

2. Действия с матрицами.

Цель занятия: приобретение базовых знаний в области фундаментального раздела математики – линейной алгебры. Закрепить на практике понятие матрицы, её виды, операции над матрицами. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ЛР 4, У₄, У₆.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₆. Владеть актуальными методами работы в профессиональной и смежных сферах.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Матрицы и определители».

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

I. Теоретический опрос по теме «Матрицы и определители».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц.

2. Алгебраические операции над матрицами: умножение на число, сложение (вычитание), умножение матриц, возведение в степень.

3. Определители 2, 3 и n-го порядков (определения и их свойства).

4. Теорема Лапласа о разложении определителя по элементам строки или столбца.

5. Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы.

II. Выполнение заданий по образцу совместно с преподавателем.

1. Даны матрицы:

Матрицы

Можно ли сложить матрицу А: с матрицей В; с матрицей С; с матрицей D?

2. Найти: А+В, если

3. Дано:

Матрица Найти: -3A.

4. Даны матрицы:

Матрицы

Найти: 2A+В-3С.

5. Найти матрицу Х, если:

Матрицы

6. Найти: a, b, c из уравнения: Матрицы

7. Выполнить действия:

Матрицы

8. Найти матрицу

если

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Действия над матрицами» в форме решения типового задания по вариантам, согласно своего номера в журнале.

Задание. Выполнить указанные действия с матрицами А и В, если

Вариант №1

Вариант №2

Вариант №3

Вариант №4

Вариант №5

Вариант №6

Вариант №7

Вариант №8

Вариант №9

Вариант №10

Вариант №11

Вариант №12

Вариант №13

Вариант №14

Вариант №15

Вариант №16

Вариант №17

Вариант №18

Вариант №19

Вариант №20

Вариант №21

Вариант №22

Вариант №23

Вариант №24

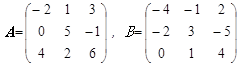
Задания по вариантам

Вопросы для закрепления.

1. Что называется матрицей? Запишите общий вид матрицы размером mxn.

2. Какие матрицы называются равными?

3. Назовите виды матриц.

4. Назовите линейные операции над матрицами.

5. Какие матрицы можно перемножать? Как выполняется умножение?

Литература: Электронный ресурс. О₁: Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 1: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 276 с. — (Профессиональное образование). — ISBN 978-5-534-10174-4. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442438 - п. 1.1 – 1.4, стр. 20.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4

Тема: «Определители второго и третьего порядков».

Тема 2.1. Матрицы и определители.

1. Определитель матрицы. Свойства определителя.

Цель занятия: формировать умения находить определители второго, третьего порядков различными способами с использованием свойств определителя. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ЛР 4, У₄, У₆.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₆. Владеть актуальными методами работы в профессиональной и смежных сферах.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Матрицы и определители».

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

I. Теоретический опрос по теме «Матрицы и определители».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц.

3. Определители 2, 3 и n-го порядков (определения и их свойства).

4. Теорема Лапласа о разложении определителя по элементам строки или столбца.

5. Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы.

II. Выполнение заданий по образцу совместно с преподавателем.

Задание 1. Найти минор М₂₃ и алгебраическое дополнение А₂₃ к элементу а₂₃ определителя

Задание 2. Вычислить определители второго порядка:

a) , b) ,

c), d).

Задание 3. Решить уравнение:

a) ;

b) .

Задание 4. Вычислить определители третьего порядка методом треугольников:

a) , b) , c) .

Задание 5. Вычислить определители методом разложения по строке (столбцу):

a) , b)

Задание 6. Вычислить определители четвертого порядка:

а) , б)

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Определители второго и третьего порядков» в форме решения типового задания по вариантам, согласно своего номера в журнале.

Задание 1. Вычислите определить второго порядка:

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6

Вариант 7

Вариант 8

Вариант 9

Вариант 10

Задание 2. Вычислите определить третьего порядка любым методом:

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6

Вариант 7

Вариант 8

Вариант 9

Вариант 10

Задание 3. Вычислите определить четвертого порядка:

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вопросы для закрепления.

1. Понятие определителя матрицы.

2. Виды и методы вычисления определителя матрицы.

3. Свойства определителя матрицы.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5

Тема: «Решение матричных уравнений».

Тема 2.2. Методы решения систем линейных уравнений.

1. Метод обратной матрицы.

Цель занятия: формировать умения вычислять миноры и алгебраические дополнения матрицы, находить обратную матрицу для заданной матрицы, решать системы линейных уравнений матричным методом. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ОК 02, ЛР 4, У₁ – У₄, У₉ – У₁₇.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

ОК 02. Использовать современные средства поиска, анализа и интерпретации информации и информационные технологии для выполнения задач профессиональной деятельности.

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₃. Определять этапы решения задачи;

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₉. Определять задачи для поиска информации;

У₁₀. Определять необходимые источники информации;

У₁₁. Планировать процесс поиска;

У₁₂. Структурировать получаемую информацию;

У₁₃. Выделять наиболее значимое в перечне информации;

У₁₄. Оценивать практическую значимость результатов поиска;

У₁₅. Оформлять результаты поиска;

У₁₆. Применять средства информационных технологий для решения профессиональных задач;

У₁₇. Использовать современное программное обеспечение.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Методы решения систем линейных уравнений».

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

I. Теоретический опрос по теме «Методы решения систем линейных уравнений».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Понятие минора и алгебраических дополнений k-го порядка.

2. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления.

3. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований.

4. Система n линейных уравнений с n переменными (общий вид). Матричная форма записи такой системы. Решение системы (определение).

5. Совместные и несовместные, определенные и неопределенные системы линейных уравнений.

6. Матричный метод решения СЛУ.

II. Выполнение заданий по образцу совместно с преподавателем.

Задание 1. Найти обратную матрицу для следующих матриц:

а) ; б)

Задание 2. Решить уравнение:

а) б)

в) г)

Задание 3. Решить систему уравнений матричным методом:

Задание 4. (дополнительно) Найдите решение системы уравнений матричным методом.

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Решение матричных уравнений» в форме расчетно-графического задания по вариантам, согласно своего номера в журнале.

Задание. Решить СЛУ матричным методом и построить геометрическую интерпретацию решения:

Вариант № 1	Вариант № 2	Вариант № 3	Вариант № 4
1 ; 2	1 2	1 ; 2	1 ; 2
Вариант № 5	Вариант № 6	Вариант № 7	Вариант № 8
1 2	1 2	1 2	1 2
Вариант № 9	Вариант № 10	Вариант № 11	Вариант № 12
1 2	1 2	1 2	1 2

Вопросы для закрепления.

1. Понятие определителя матрицы. Виды и методы вычисления определителя матрицы. Свойства определителя матрицы.

2. Понятие минора и алгебраических дополнений для матрицы. Метод их вычисления.

3. Понятие обратной матрицы. Алгоритм вычисления обратной матрицы.

4. Понятие СЛУ.

5. Решение СЛУ матричным методом.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6

Тема: «Формулы Крамера (для систем линейных уравнений с тремя неизвестными)».

Тема 2.2. Методы решения систем линейных уравнений.

1. Правило Крамера.

Цель занятия: формировать умение решать систем трех линейных уравнений с тремя неизвестными с помощью определителей (методом Крамера), систематизировать знания по выполнению операций над матрицами: сложение, вычитание, умножение матрицы на число, произведение матриц; формировать умения находить определители матриц. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ОК 02, ЛР 4, У₁ – У₄, У₉ – У₁₅.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₃. Определять этапы решения задачи;

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₉. Определять задачи для поиска информации;

У₁₀. Определять необходимые источники информации;

У₁₁. Планировать процесс поиска;

У₁₂. Структурировать получаемую информацию;

У₁₃. Выделять наиболее значимое в перечне информации;

У₁₄. Оценивать практическую значимость результатов поиска;

У₁₅. Оформлять результаты поиска.

Требования к выполнению практической работы:

1. Выполнить тест № 2 по темам «Матрицы и определители. Методы решения систем линейных уравнений» в двух вариантах, согласно своего номера в журнале.

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

I. Выполнить тест № 2 по темам «Матрицы и определители. Методы решения систем линейных уравнений».

Тест состоит из 10 вопросов в двух вариантах, вариант необходимо выбрать, согласно своего номера в журнале. За 2 правильных ответа – 1 балл. Максимальное количество баллов – 5.

II. Выполнение заданий по образцу совместно с преподавателем.

Задание 1. Решить систему уравнений методом Крамера:

Задание 2. Задача:

Обувная фабрика специализируется по выпуску изделий трёх видов: сапог, кроссовок и ботинок; при этом используется сырьё трёх типов. Нормы расхода каждого из них на одну пару обуви и объём расхода сырья на один день заданы таблицей:

Виды сырья	Нормы расхода сырья на одну пару			Норма расхода сырья на один день, усл. ед.
Виды сырья	Сапоги	Кроссовки	Ботинки	Норма расхода сырья на один день, усл. ед.
1	5	3	4	2700
2	2	1	1	900
3	3	2	2	1600

Найти ежедневный объём выпуска каждого вида обуви.

Задание 3. Решить систему уравнений методом Крамера:

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Формулы Крамера (для систем линейных уравнений с тремя неизвестными)» в форме расчетно-графического задания по вариантам, согласно своего номера в журнале.

Задание. Решить СЛУ методом Крамера и построить геометрическую интерпретацию решения:

Вариант № 1	Вариант № 2	Вариант № 3	Вариант № 4
1 2	1 2	1 2	1 2
Вариант № 5	Вариант № 6	Вариант № 7	Вариант № 8
1 2	1 2	1 2	1 2
Вариант № 9	Вариант № 10	Вариант № 11	Вариант № 12
1 2	1 2	1 2	1 2

Вопросы для закрепления.

2. Понятие СЛУ.

3. Решение СЛУ методом определителей.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7, 8

Тема: «Метод Гаусса (метод исключения неизвестных)».

Тема 2.2. Методы решения систем линейных уравнений.

1. Метод Гаусса.

Цель занятия: формировать навыки решения систем трех линейных уравнений с тремя неизвестными с помощью метода Гаусса, систематизировать знания и умения по выполнению операций над матрицами (сложение, вычитание, умножение матрицы на число, произведение матриц). Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ОК 02, ЛР 4, У₁ – У₄, У₉ – У₁₇.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₃. Определять этапы решения задачи;

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₉. Определять задачи для поиска информации;

У₁₀. Определять необходимые источники информации;

У₁₁. Планировать процесс поиска;

У₁₂. Структурировать получаемую информацию;

У₁₃. Выделять наиболее значимое в перечне информации;

У₁₄. Оценивать практическую значимость результатов поиска;

У₁₅. Оформлять результаты поиска;

У₁₆. Применять средства информационных технологий для решения профессиональных задач;

У₁₇. Использовать современное программное обеспечение.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Методы решения систем линейных уравнений».

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

I. Теоретический опрос по теме «Методы решения систем линейных уравнений».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Понятие минора и алгебраических дополнений k-го порядка.

2. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления.

3. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований.

5. Совместные и несовместные, определенные и неопределенные системы линейных уравнений.

6. Матричный метод решения СЛУ.

7. Правило Крамера или метод определителей для решения СЛУ.

8. Метод Гаусса решения СЛУ.

II. Выполнение заданий по образцу совместно с преподавателем.

Задание 1. Найдите решение системы уравнений методом Гаусса.

Задание 2. Решите систему из трех уравнений методом Гаусса:

формула

Задание 3. Задача:

Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй - 30%, третий - 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Метод Гаусса (метод исключения неизвестных)» в форме расчетно-графического задания по вариантам, согласно своего номера в журнале.

Задание. Решить СЛУ методом Гаусса и построить геометрическую интерпретацию решения:

Вариант № 1	Вариант № 2	Вариант № 3	Вариант № 4
1 2	1 2	1 2	1 2
Вариант № 5	Вариант № 6	Вариант № 7	Вариант № 8
1 2	1 2	1 2	1 2
Вариант № 9	Вариант № 10	Вариант № 11	Вариант № 12
1 2	1 2	1 2	1 2

Вопросы для закрепления.

1. Что называется матрицей? Запишите общий вид матрицы размером mxn.

2. Какие матрицы называются равными?

3. Назовите виды матриц.

4. Назовите линейные операции над матрицами.

5. Какие матрицы можно перемножать? Как выполняется умножение?

6. Вычисление определителей.

7. Вычисление обратной матрицы.

8. Алгоритм решения СЛУ с помощью определителей, метода Гаусса, матричного метода.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9

Тема: «Экстремум функции нескольких переменных».

Тема 3.1. Пределы и непрерывность.

Тема 3.2. Производная и дифференциал.

1. Предел функции.

2. Бесконечно малые функции.

3. Метод эквивалентных бесконечно малых величин.

4. Раскрытие неопределённости вида 0/0 и ∞/∞.

5. Замечательные пределы.

6. Непрерывность функции.

7. Производная функции.

8. Первый дифференциал функции, связь с приращением функции.

9. Основные правила дифференцирования.

10. Производные и дифференциалы высших порядков.

11. Возрастание и убывание функций.

12. Экстремумы функций.

13. Частные производные функции нескольких переменных.

14. Полный дифференциал.

15. Частные производные высших порядков.

Цель занятия: научиться находить производные функций, исследовать функции с помощью производных; исследовать функции нескольких переменных на максимум и минимум с использованием производных высших порядков; вывести алгоритм нахождения наименьшего и наибольшего значений функции; решать задачи на отыскание наибольших и наименьших значений функции. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ЛР 4, У₄, У₅, У₇, У₈.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₄.Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₅.Составить план действия; определить необходимые ресурсы;

У₇.Реализовать составленный план;

У₈.Оценивать результат и последствия своих действий (самостоятельно или с помощью наставника).

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по темам «Функции многих переменных. Пределы и непрерывность. Производная и дифференциал».

2. Выполнить тест № 3 по темам «Функции многих переменных. Пределы и непрерывность. Производная и дифференциал» в четырех вариантах согласно своего номера в журнале.

3. Оформить задания в тетради для практических работ.

4. Выполнить задания по образцу совместно с преподавателем.

5. Выполнить индивидуальное задание по варианту в тетради для практических работ.

6. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

I. Теоретический опрос по темам «Функции многих переменных. Пределы и непрерывность. Производная и дифференциал».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Предел и непрерывность функции двух переменных.

2. Дифференцирование функций.

3. Дифференциалы функций нескольких переменных.

4. Дифференцирование сложных функций.

5. Дифференцирование неявных функций.

6. Производная функции в данном направлении. Градиент функции.

7. Касательная плоскость и нормаль к поверхности.

8. Экстремумы функции двух переменных.

9. Определение числовой последовательности.

10. Предел числовой последовательности.

12. Свойства предела.

13. Определение предела функции.

14. Свойства предела функции.

15. Методы вычисления предела функции.

16. Бесконечно малые и бесконечно большие функции.

17. Непрерывность функции в точке и на интервале.

18. Производная функции. Первый дифференциал функции, связь с приращением функции.

19. Основные правила дифференцирования.

20. Производные и дифференциалы высших порядков.

21. Возрастание и убывание функций. Экстремумы функций.

22. Частные производные функции нескольких переменных. Полный дифференциал. Частные производные высших порядков.

II. Выполнить тест № 3 по темам «Функции многих переменных. Пределы и непрерывность. Производная и дифференциал».

Тест состоит из 10 вопросов в четырех вариантах, вариант необходимо выбрать, согласно своего номера в журнале. За 2 правильных ответа – 1 балл. Максимальное количество баллов – 5.

III. Выполнение заданий по образцу совместно с преподавателем.

Задание 1. Найти экстремумы функции и наибольшее (наименьшее) значение функции на заданном промежутке f(x)=x³-12x+2; [0;6].

Задание 2. Найти наибольшее и наименьшее значения функции на интервале

Задание 3. Решить задачу. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найти значение f^‘(x₀).

Задание 4. Найти производную функции:

1) ; 2) ; 3) ;

Задание 5. Вычислите производную функции в заданных точках:

1) в точках х = 0, х = - 1, х = 2

2) в точке .

Задание 6. Применяя теоремы дифференцирования и таблицу для производных, вычислите производные функции:

1) ; 2) ; 3) .

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Экстремум функции нескольких переменных» в форме расчетно-графического задания по вариантам, согласно своего номера в журнале.

Задание. Исследуйте функцию с помощью производной и постройте ее график.
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

Вопросы для закрепления.

1. Понятие экстремума функции.

2. Необходимое условии экстремума.

3. Достаточное условие экстремума функции.

4. Алгоритм исследования функции с помощью производной.

5. Общая схема исследования функции с помощью производной.

Литература:

1. Электронный ресурс. О₃Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440 - п.9.1 - 9.16, стр.10.

2. Электронный ресурс. О_2:Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 2: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 241 с. — (Профессиональное образование). — ISBN 978-5-534-10173-7. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442439 - п. 6.1 – 6.10, стр.40; п. 7.1 – 7.14, 8.1 – 8.15, стр.90.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10

Тема: «Нахождение неопределённого интеграла, используя его свойства».

Тема 4.1. Неопределённый интеграл.

1. Первообразная функция и неопределённый интеграл.

2. Основные правила неопределённого интегрирования.

Цель занятия: формировать умения обучающихся вычислять неопределенные интегралы, используя свойства и таблицу неопределенных интегралов. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ЛР 4, У₁, У₂, У₃, У₆.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₃. Определять этапы решения задачи;

У₆. Владеть актуальными методами работы в профессиональной и смежных сферах.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Неопределённый интеграл».

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

I. Теоретический опрос по темам «Неопределённый интеграл».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Первообразная функция и неопределённый интеграл.

2. Геометрический смысл неопределённого интеграла.

3. Свойства неопределённого интеграла.

4. Таблица основных неопределённых интегралов.

5. Методы интегрирования (метод замены переменной в неопределённом интеграле, интегрирование подведением под знак дифференциала, метод интегрирования по частям, интегрирование дробей и др.)

II. Выполнение заданий по образцу совместно с преподавателем.

Используя основные свойства неопределенного интеграла, вычислить интегралы:
а) ;	б) ;	в) ;	г)
д) ;	е) ;	ж) ;	и) .

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Нахождение неопределённого интеграла, используя его свойства» в форме решения типового задания по вариантам, согласно своего номера в журнале.

Задание: Используя основные правила интегрирования и таблицу интегралов, вычислить следующие неопределенные интегралы:

Вариант

№ 1

а) ;

б) ;

в) .

Вариант

№ 5

а) ;

б) ;

в).

Вариант

№ 2

а) ;

б) ;

в) .

Вариант

№ 6

а) ;

б) ;

в) dx.

Вариант

№ 3

а) ;

б) ;

в) .

Вариант

№ 7

а) ;

б) ;

в) .

Вариант

№ 4

а) ;

б);

в) .

Вариант

№ 8

а) ;

б) ;

в) .

Вопросы для закрепления.

1. Сформулируйте определение первообразной функции и перечислите свойства первообразной.

2. Приведите примеры функций, имеющих и не имеющих первообразных.

3. Приведите примеры двух различных первообразных для одной и той же функции .

4. Найдите первообразную для функции , которая в точке принимает значение, равное 10.

5. Сформулируйте определение неопределенного интеграла.

6. В чем состоит геометрический смысл неопределенного интеграла?

7. Перечислите свойства неопределенного интеграла.

Литература: Электронный ресурс. О_3:Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440 - п. 10.1 – 10.14, стр.70.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 11

Тема: «Методы замены переменной и интегрирования по частям».

Тема 4.1. Неопределённый интеграл.

1. Первообразная функция и неопределённый интеграл.

2. Основные правила неопределённого интегрирования.

Цель занятия: формировать умения обучающихся вычислять неопределенные интегралы, используя свойства и таблицу неопределенных интегралов, а также методы замены переменной и интегрирования по частям. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ЛР 4, У₁, У₂, У₃, У₆.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₃. Определять этапы решения задачи;

У₆. Владеть актуальными методами работы в профессиональной и смежных сферах.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Неопределённый интеграл».

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

Теоретический опрос по темам «Неопределённый интеграл».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Первообразная функция и неопределённый интеграл.

2. Геометрический смысл неопределённого интеграла.

3. Свойства неопределённого интеграла.

4. Таблица основных неопределённых интегралов.

II. Выполнение заданий по образцу совместно с преподавателем.

1. С помощью метода замены переменной найти интегралы:
а) ;	б) ;	в) ;	г) ;
д) ;	е) ;	ж) ;	и) .
2. Используя метод интегрирования по частям, вычислить следующие интегралы:
а) ;	б) ;	в) ;	г) ;
д) ;	е) .

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Методы замены переменной и интегрирования по частям» в форме решения типового задания по вариантам, согласно своего номера в журнале.

Задание 1. Используя метод замены переменной, вычислить следующие неопределенные интегралы:
Вариант № 1	а) ; б) .	Вариант № 5	а) ; б) .
Вариант № 2	а) ; б).	Вариант № 6	а) ; б) .
Вариант № 3	а) ; б) .	Вариант № 7	а) ; б) .
Вариант № 4	а) ; б) .	Вариант № 8	а); б).
Задание 2. Используя метод интегрирования по частям, вычислить следующие неопределенные интегралы:
Вариант № 1	.	Вариант № 5	.
Вариант № 2	.	Вариант № 6	.
Вариант № 3	.	Вариант № 7	.
Вариант № 4	.	Вариант № 8	.

Вопросы для закрепления.

1. Перечислите свойства неопределенного интеграла.

2. Как осуществляется интегрирование с помощью замены переменной?

3. Как осуществляется интегрирование с помощью интегрирования по частям?

4. Какие подынтегральные функции удобно интегрировать по частям?

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 12, 13

Тема: «Правила замены переменной и интегрирования по частям».

Тема 4.2. Определённый интеграл.

1. Задача нахождения площади криволинейной трапеции.

2. Определённый интеграл.

3. Формула Ньютона-Лейбница.

4. Основные свойства определённого интеграла.

Цель занятия: формировать умения обучающихся вычислять определенные интегралы, используя свойства и таблицу неопределенных интегралов, а также методы непосредственного интегрирования, замены переменной и интегрирования по частям; формировать умения вычислять площади фигур, ограниченных линиями с помощью определенного интеграла. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ЛР 4, У₄, У₅, У₇.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₅. Составить план действия; определить необходимые ресурсы;

У₇. Реализовать составленный план.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Определённый интеграл».

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

Теоретический опрос по темам «Определённый интеграл».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. Понятие определенного интеграла.

2. Основные свойства определенного интеграла.

3. Методы вычисления определенного интеграла. (Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле.

Интегрирование по частям. Интегрирование четной и нечетной функции по симметричному промежутку).

4. Несобственные интегралы первого и второго рода.

5. Прикладные задачи для определенного интеграла.

(Площадь плоских фигур в декартовой системе координат. Формула вычисления длины дуги кривой. Формула вычисления объема фигуры вращения, образованной вращением линии вокруг координатной оси).

II. Выполнение заданий по образцу совместно с преподавателем.

Задание 1. Используя метод непосредственного интегрирования, вычислить следующие определенные интегралы:
1.			2.			3.	4.		5.
6.			7.
Задание 2. Используя метод замены переменной, вычислить следующие определенные интегралы:
1.		2.			3.		4.	5.
Задание 3. Используя метод интегрирования по частям, вычислить следующие определенные интегралы:
1.	2.		3.			4.	5.	6.
Задание 4. Вычислите площадь фигуры, с помощью определенного интеграла. Сделайте чертеж.
1. Найти площадь фигуры, ограниченной линиями y = e^{– x}, y = 0, x = 0, x = ln 3.				2. Вычислить площадь фигуры, ограниченной линиями и .

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Правила замены переменной и интегрирования по частям» в форме решения типового задания по вариантам согласно своего номера в журнале.

Задание 1. Используя метод непосредственного интегрирования, вычислить следующие определенные интегралы:
Вариант № 1		Вариант № 5		Вариант № 9
Вариант № 2		Вариант № 6		Вариант № 10
Вариант № 3		Вариант № 7		Вариант № 11
Вариант № 4		Вариант № 8		Вариант № 12
Задание 2. Используя метод замены переменной, вычислить следующие определенные интегралы:
Вариант № 1		Вариант № 5		Вариант № 9
Вариант № 2		Вариант № 6		Вариант № 10
Вариант № 3		Вариант № 7		Вариант № 11
Вариант № 4		Вариант № 8		Вариант № 12
Задание 3. Используя метод интегрирования по частям, вычислить следующие определенные интегралы:
Вариант № 1		Вариант № 5		Вариант № 9
Вариант № 2		Вариант № 6		Вариант № 10
Вариант № 3		Вариант № 7		Вариант № 11
Вариант № 4		Вариант № 8		Вариант № 12
Задание 4. Вычислите площадь фигуры, ограниченной параболой у=ах²+bх+с и прямой у=kх+b. Сделайте чертеж:
Вариант № 1	у = - х² + 4х - 1; у = - х - 1.		Вариант № 6	у = х² + 6х + 7; у = х + 7
Вариант № 2	у = х² - 6х + 7; у = х + 1		Вариант № 7	у = - х² - 6х - 5; у = х + 1
Вариант № 3	у = - х² + 6х -5; у = х - 5		Вариант № 8	у = х² + 6х + 7; у = - х + 1
Вариант № 4	у = х² - 6х + 7; у = - х + 7		Вариант № 9	у = - х² - 6х - 6; у = - х - 6
Вариант № 5	у = - х² + 6х - 5; у = - х + 1		Вариант № 10	у = х² - 4х + 1; у = х + 1

Вопросы для закрепления.

1. Что называют определенным интегралом функции f(x)?

2. В чем состоит геометрический смысл определенного интеграла?

3. Сформулируйте необходимое условие интегрируемости функции f(x) на отрезке [a,b].

4. Сформулируйте необходимое и достаточное условия интегрируемости функции f(x) на отрезке [a, b].

5. Запишите свойства определенного интеграла.

6. Запишите формулу Ньютона-Лейбница.

7. Расскажите об основных методах интегрирования определенного интеграла.

8. Площадь криволинейной трапеции. Алгоритм вычисления.

9. Применение определенного интеграла в экономических задачах.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 14, 15

Тема: «Дифференциальные уравнения первого порядка и первой степени».

Тема 4.3. Дифференциальные уравнения.

1. Примеры задач, приводящих к дифференциальным уравнениям.

2. Основные понятия и определения.

Цель занятия: формировать умения обучающихся определять вид и способ решения дифференциального уравнения, формировать навыки решения ДУ с разделяющими переменными, линейного однородного ДУ первого и второго порядка. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ОК 02, ЛР 4, У₁, У₂, У₅, У₇ - У₁₅.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₅. Составить план действия; определить необходимые ресурсы;

У₇. Реализовать составленный план;

У₈. Оценивать результат и последствия своих действий (самостоятельно или с помощью наставника);

У₉. Определять задачи для поиска информации;

У₁₀. Определять необходимые источники информации;

У₁₁. Планировать процесс поиска;

У₁₂. Структурировать получаемую информацию;

У₁₃. Выделять наиболее значимое в перечне информации;

У₁₄. Оценивать практическую значимость результатов поиска;

У₁₅. Оформлять результаты поиска.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Дифференциальные уравнения».

2. Оформить задания в тетради для практических работ.

3. Выполнить задания по образцу совместно с преподавателем.

4. Выполнить индивидуальное задание по варианту в тетради для практических работ.

5. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

Теоретический опрос по темам «Дифференциальные уравнения».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. История ДУ. Задачи, приводящие к ДУ.

2. Обыкновенные дифференциальные уравнения. Основные определения. Свойства общего решения. Теорема Коши. Интегральные кривые. Особое решение.

3. Дифференциальные уравнения первого порядка. Уравнения вида у’ = f(х). Уравнения с разделяющимися переменными. Однородные уравнения. Уравнения, приводящиеся к однородным. Линейные уравнения. Линейные однородные дифференциальные уравнения. Линейные неоднородные дифференциальные уравнения. Метод Бернулли. Метод Лагранжа. Уравнение Бернулли.

4. Уравнения в полных дифференциалах. Условие тотальности.

5. Геометрическая интерпретация решений дифференциального уравнения первого порядка. Поле направлений. Изоклины.

6. Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка. Уравнения вида y⁽ⁿ⁾ = f(x). Линейные дифференциальные уравнения высших порядков. Линейные однородные дифференциальные уравнения с произвольными коэффициентами. Структура общего решения. Фундаментальна система решений. Определитель Вронского. Общее решение линейного однородного дифференциального уравнения второго порядка. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.

II. Выполнение заданий по образцу совместно с преподавателем.

1.Дифференциальные уравнения с разделяющимися переменными
Пример 1. Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию	Пример 2. Решить дифференциальное уравнение . Найти частное решение уравнения, удовлетворяющее начальным данным: при x=1, y=1.	Пример 3. Решить дифференциальное уравнение:		Пример 4. Решить уравнение , при начальных условиях .
Пример 5. Решить задачу Коши:	Пример 6. Решите дифференциальное уравнение: .	Пример 7. Решите дифференциальное уравнение: ,
2.Прикладные задачи, приводящие к дифференциальным уравнениям.
Задача 1. Найти кривую, обладающую тем свойством, что отрезок любой ее касательной, заключенной между осями координат, делится пополам в точке касания	Задача 2.(радиоактивный распад). Экспериментальным путем установлено, что скорость радиоактивного распада пропорциональна количеству нераспавшегося вещества. Считая, что начальное количество вещества равно М₀, найти зависимость между количеством нераспавшегося вещества М и временем t.		Задача 3. (охлаждение тела). Согласно закону, установленному Ньютоном, скорость охлаждения тела пропорциональна разности между температурой тела и температурой окружающей среды. Требуется получить закон (аналитический вид) охлаждения тела.

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Дифференциальные уравнения первого порядка и первой степени» в форме решения типового задания по вариантам, согласно своего номера в журнале.

Задание 1. Найдите общее решение дифференциальных уравнений:
Вариант № 1		Вариант № 4
Вариант № 1		Вариант № 4
Вариант № 2		Вариант № 5
Вариант № 2		Вариант № 5
Вариант № 3		Вариант № 6
Вариант № 3		Вариант № 6
Задание 2. Найдите частные решения дифференциальных уравнений, удовлетворяющие указанным начальным условиям:
Вариант № 1		Вариант № 4
Вариант № 2		Вариант № 5
Вариант № 3		Вариант № 6

Вопросы для закрепления.

Какое уравнение называется дифференциальным?

2. Что называется решением дифференциального уравнения?

3. Какое решение дифференциального уравнения называется общим?

4. Какое решение дифференциального уравнения называется частным?

5. Какие дифференциальные уравнения называются уравнениями первого порядка?

6. Какие дифференциальные уравнения называются уравнениями с разделяющимися переменными?

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 16

Тема: «Уравнения с разделяющимися переменными».

Тема 4.3. Дифференциальные уравнения.

1. Примеры задач, приводящих к дифференциальным уравнениям.

2. Основные понятия и определения.

Цель занятия: продолжить формировать умения обучающихся определять вид и способ решения дифференциального уравнения, формировать навыки решения ДУ с разделяющими переменными, линейного однородного ДУ первого и второго порядка. Овладеть учебно-познавательными компетенциями (умение планировать, анализировать, самостоятельно добывать знания) и коммуникативными компетенциями (умение ясно и четко излагать мысли, убеждать, аргументировать, строить доказательства, анализировать, высказывать суждения, передавать рациональную и эмоциональную информацию) для владения умениями описания свойств различных процессов и явлений математического характера.

Сформированные компетенции: ОК 01, ОК 02, ЛР 4, У₁, У₂, У₅, У₇ - У₁₅.

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₅. Составить план действия; определить необходимые ресурсы;

У₇. Реализовать составленный план;

У₈. Оценивать результат и последствия своих действий (самостоятельно или с помощью наставника);

У₉. Определять задачи для поиска информации;

У₁₀. Определять необходимые источники информации;

У₁₁. Планировать процесс поиска;

У₁₂. Структурировать получаемую информацию;

У₁₃. Выделять наиболее значимое в перечне информации;

У₁₄. Оценивать практическую значимость результатов поиска;

У₁₅. Оформлять результаты поиска.

Требования к выполнению практической работы:

1. Сдать теоретический срез знаний по теме «Дифференциальные уравнения».

2. Выполнить тест № 4 по темам «Неопределенный интеграл. Определенный интеграл. Дифференциальные уравнения» в четырех вариантах, согласно своего номера в журнале.

3. Оформить задания в тетради для практических работ.

4. Выполнить задания по образцу совместно с преподавателем.

5. Выполнить индивидуальное задание по варианту в тетради для практических работ.

6. Ответить на контрольные теоретические вопросы.

Содержание практической работы.

Теоретический опрос по темам «Дифференциальные уравнения».

Обучающиеся отвечают на вопросы в письменной (устной) форме.

Вопросы обучающимся:

1. История ДУ. Задачи, приводящие к ДУ.

4. Уравнения в полных дифференциалах. Условие тотальности.

I. Выполнить тест № 4 по темам «Неопределенный интеграл. Определенный интеграл. Дифференциальные уравнения».

III. Выполнение заданий по образцу совместно с преподавателем.

1.Дифференциальные уравнения с разделяющимися переменными
Пример 1. Найти общие решения ДУ с разделяющимися переменными: а); б); в); г).	Пример 2. Решить уравнение:		Пример 3. Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию . Выполнить проверку.
	Пример 4. Решить дифференциальное уравнение . Ответ представить в виде общего интеграла .		Пример 5. Решить дифференциальное уравнение . Выполнить проверку.
2. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
Пример 1. Найти фундаментальную систему решений и общее решение: 3y′′−2y′- y=0	Пример 2. Найти фундаментальную систему решений и общее решение: 9y′′+6y′+y=0.	Пример 3. Найти фундаментальную систему решений и общее решение: y′′+6y′+13y=0		Пример 4. Решить задачу Коши:

Индивидуальная работа по вариантам.

Выполнить индивидуальную работу по теме «Уравнения с разделяющимися переменными» в форме решения типового задания по вариантам согласно своего номера в журнале.

Задание 1. Найти частное решение дифференциального уравнения с разделяющимися переменными:
Вариант № 1		Вариант № 4
Вариант № 2		Вариант № 5
Вариант № 3		Вариант № 6
Задание 2. Найти фундаментальную систему решений и общее решение линейного однородного ДУ с постоянными коэффициентами:
Вариант № 1	y′′−5y′+6y=0	Вариант № 4	y′′+4y′+4y=0
Вариант № 1	y′′−6y′+9y=0	Вариант № 4	y′′− y′−2y=0
Вариант № 2	y′′−3y′=0	Вариант № 5	y′′−4y′+4y=0
Вариант № 2	y′′+4y′+13y=0	Вариант № 5	y′′−6y′-9y=0
Вариант № 3	y′′−25y′=0	Вариант № 6	y′′-25y=0;
Вариант № 3	y′′−2y′+10y=0	Вариант № 6	y′′+5y′+6y=0

Вопросы для закрепления.

1. Какое уравнение называется дифференциальным?

2. Что называется решением дифференциального уравнения?

3. Какое решение дифференциального уравнения называется общим?

4. Какое решение дифференциального уравнения называется частным?

5. Какие дифференциальные уравнения называются уравнениями первого порядка?

6. Какие дифференциальные уравнения называются уравнениями с разделяющимися переменными?

7. Теорема Коши.

8. Понятие линейного однородного дифференциального уравнения и его виды.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 17

Тема: «Итоговая контрольная работа».

Темы:

1.1. Комплексные числа и действия над ними.

2.1. Матрицы и определители.

2.2. Методы решения систем линейных уравнений.

3.1. Пределы и непрерывность.

3.2. Производная и дифференциал.

4.1. Неопределённый интеграл.

4.2. Определённый интеграл.

4.3. Дифференциальные уравнения.

Цель: систематизация и контроль полученных знаний и умений обучающихся по: понятию комплексных чисел и действиях над ними; понятию матриц и действиях над матрицами, по понятию определителя матрицы и способам его вычисления, по понятию и методам решения систем линейных алгебраических уравнениях; по понятию предела и производной функции и по способам их вычисления, по применению производной к исследованию функций и построению их графиков; по понятию определенного и неопределенного интеграла и методам их вычисления и применения; по понятию и видам дифференциальных уравнений и методам их решения в зависимости от их вида.

Сформированные компетенции: ОК 01, ОК 02, ЛР 4, У₁ - У₁₇, З₁ - З₁₀.

ОК 01 Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

ОК 02 Использовать современные средства поиска, анализа и интерпретации информации и информационные технологии для выполнения задач профессиональной деятельности.

У₁. Распознавать задачу и/или проблему в профессиональном и/или социальном контексте;

У₂. Анализировать задачу и/или проблему и выделять её составные части;

У₃. Определять этапы решения задачи;

У₄. Выявлять и эффективно искать информацию, необходимую для решения задачи и/или проблемы;

У₅. Составить план действия; определить необходимые ресурсы;

У₆. Владеть актуальными методами работы в профессиональной и смежных сферах;

У₇. Реализовать составленный план;

У₈. Оценивать результат и последствия своих действий (самостоятельно или с помощью наставника);

У₉. Определять задачи для поиска информации;

У₁₀. Определять необходимые источники информации;

У₁₁. Планировать процесс поиска;

У₁₂. Структурировать получаемую информацию;

У₁₃. Выделять наиболее значимое в перечне информации;

У₁₄. Оценивать практическую значимость результатов поиска;

У₁₅. Оформлять результаты поиска;

У₁₆. Применять средства информационных технологий для решения профессиональных задач;

У₁₇. Использовать современное программное обеспечение.

З₁. Актуальный профессиональный и социальный контекст, в котором приходится работать и жить;

З₂. Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;

З₃. Алгоритмы выполнения работ в профессиональной и смежных областях;

З₄. Методы работы в профессиональной и смежных сферах;

З₅. Структуру плана для решения задач;

З₆. Порядок оценки результатов решения задач профессиональной деятельности;

З₇. Номенклатуру информационных источников применяемых в профессиональной деятельности;

З₈. Приемы структурирования информации;

З₉. Формат оформления результатов поиска информации;

З₁₀. Современные средства и устройства информатизации; порядок их применения и программное обеспечение в профессиональной деятельности.

Рекомендуемая литература:

Название источника	Страницы
О₁. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 1: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 276 с. — (Профессиональное образование). — ISBN 978-5-534-10174-4. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442438
О₂. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 2: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 241 с. — (Профессиональное образование). — ISBN 978-5-534-10173-7. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442439
О₃. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440

Рекомендации по выполнению итоговой контрольной работы.

Для выполнения контрольной работы вначале изучается теория и приведенные примеры решения задач. Изучение теории ведется по учебникам, приведенным в учебной программе, или по любым другим учебникам, содержащим вопросы учебной программы.

Задания для контрольной работы разработаны в количестве 14 вариантов в соответствии с учебной программой учебной дисциплины.

Вариант работы выбирается по номеру обучающегося в журнале. Каждый вариант содержит 4 основных задания и 1 дополнительное (задание со звездочкой). Решения должны быть четкими, логически последовательными. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, с указанием используемых формул.

Качество контрольной работы оценивается, прежде всего, по тому, насколько правильно и самостоятельно решены задачи и в какой степени используется рекомендованная литература.

При выполнении заданий надо помнить следующее:

- работа выполняется на двойных листочках в клеточку; следует пронумеровать страницы и оставить на них поля не менее 3 см для замечаний преподавателя;

- на первой странице должен быть прикреплен титульный лист утвержденного образца или аккуратно записаны все данные титульного листа: учебная дисциплина и специальность, фамилия, имя, отчество обучающегося, номер группы, вариант;

- работа должна быть выполнена чернилами одного цвета, аккуратно, разборчиво;

- решение задач желательно располагать в порядке номеров, указанных в задании, номера задач следует указывать перед условием;

- условия задач должны быть обязательно переписаны полностью;

- при оформлении записей в работе необходимо выполнять общие требования к культуре их ведения, а именно:

- соблюдать абзацы, каждую новую мысль начинать с красной строки;

- используемые формулы, равенства, определения записывать в отдельной строке, чтобы сделать их более обозримыми;

- правильно употреблять символы и термины;

- в описании решения задач краткую запись условия отделять от решения, а в конце решения писать ответ;

- чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.

Контрольная работа должна быть выполнена в срок, соответствующий учебному графику.

Задания итоговой контрольной работы

1. а) Представить комплексное число в тригонометрической и показательной форме;

б) Выполнить действия z₁ z₂, z₁ - z₂, z₁ ∙ z₂, над комплексными числами.

Вариант №	Задание
0	а) z = 4 + i ;	б) z₁= 3 i и z₂= 2 i .
1	а) z = - 1+ i ;	б) z₁= 15 3i и z₂= 2 i.
2	а) z = - 6i ;	б) z₁= 10 3i и z₂= 2 0,5i .
3	а) z = - + i ;	б) z₁= 10 и z₂= 2 - i .
4	а) z = 8i ;	б) z₁= 1 i и z₂= 2 i .
5	а) z = - 2 + i ;	б) z₁= - 1 i и z₂= 6 i .
6	а) z = 2 + 2 i ;	б) z₁=5i и z₂= 3 i .
7	а) z = 8 - i ;	б) z₁= 3i и z₂= 7 i .
8	а) z = 1 + i ;	б) z₁= 10 3i и z₂= i .
9	а) z = 5 + 5 i ;	б) z₁= 1 3i и z₂= 1 i .
10	а) z = -1 - i ;	б) z₁= - 1 i и z₂= 2 i.
11	а) z = - i ;	б) z₁= 3 3i и z₂= 2 i .
12	а) z = - i ;	б) z₁= 1 и z₂= 2 i .
13	а) z = 1 + i ;	б) z₁= - 3i и z₂= 5 i .
14	а) z = + i ;	б) z₁= 1 - 3i и z₂= 2 - i .

2. Решить систему уравнений:

а) по формулам Крамера;

б) методом Гаусса.

Вариант №	Задание	Вариант №	Задание
0		8
1		9
2		10
3		11
4		12
5		13
6		14
7

3. Вычислить пределы:

Вариант №	Задание
0	а) б)
1	а) б)
2	а) б)
3	а) б)
4	а) б)
5	а) б)
6	а) б)
7	а) б)
8	а) б)
9	а) б)
10	а) б)
11	а) б)
12	а) б)
13	а) б)
14	а) б)

4.* Найти частные производные и полные дифференциалы первого и второго порядка для данной функции:

Вариант №	Задание	Вариант №	Задание
0		8
1		9
2		10
3		11
4		12
5		13
6		14
7

5. Найти общее или частное решение дифференциального уравнения:

Вариант №	Задание
0	если у = 3 при х = 0;
1
2	если у = 5 при х = 0;
3	если у = 8 при х = 0;
4	, если у(2) = 2;
5	б) если у = 11 при х = 0;
6
7	если у = 7 при х = 0;
8	если у = 15 при х = 0;
9
10	если у = 14 при х = 0;
11	если у = 2 при х = 0;
12	если у = 12 при х = 0;
13	;
14	;

Пример варианта № 0 контрольной работы

1. а) Представить комплексное число в тригонометрической и показательной форме: z = 4 - i.

б) Выполнить действия z₁ z₂, z₁ - z₂, z₁ ∙ z₂, над комплексными числами z₁= 1 3i и z₂= 2 i .

2. а) Решить систему линейных уравнений по формулам Крамера:

б) Решить систему линейных уравнений методом Гаусса:

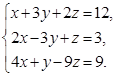
3. Вычислить пределы:

а)	б)	в)
г)	д)	е)
ж)	з)	и)

4.* Найти частные производные и полные дифференциалы первого и второго порядка функции

5. Найти общее или частное решение дифференциального уравнения:

а) ;

б) , ;

в) , если у = 1, =5 при х = 0.

Показатели выполнения контрольной работы

Решение варианта № 0 контрольной работы

1 а) Представить комплексное число в тригонометрической и показательной форме: z = 4 - i.

Решение. Находим модуль числа z, используя формулу

r = = = 8.

Находим аргумент φ, используя формулу tg φ =:

tg φ = - и число z лежит в IV четверти. Изображение числа z на комплексной плоскости представлено на рисунке 1.

Поэтому φ = arctg(- ) = .

рис. 1 Геометрическая интерпретация

Подставим полученные значения и φ для получения тригонометрической формы записи данного комплексного числа:

z = 8( cos ( - ) sin( - ) ) .

По формуле показательной формы записи комплексного числа имеем:

z = 8 .

1 б) Выполнить действия z₁ z₂, z₁ - z₂, z₁ ∙ z₂, над комплексными числами z₁= 1 3i и z₂= 2 i .

Решение. Используя определение суммы и разности комплексных чисел

z₁ z₂= (х₁ х₂) i (у₁ у₂) и z₁ z₂= (х₁ х₂) i (у₁ у₂),

найдем:

z₁ z₂ = ( 1 ) = 3 .

z₁ - z₂ = ( 1 ) = - 1 .

Для нахождения произведения комплексных чисел следует учесть следующее соотношение: .

Тогда

z₁ ∙ z₂= (1 3i)( 2 i) = 2 1i 6i3=2 7i 3=1 7i.

При делении можно использовать свойство сопряженных комп-лексных чисел:

2 а) Решить систему линейных уравнений по формулам Крамера:

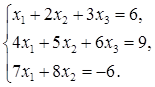
Решение. Вычислим определитель матрицы системы и определители при неизвестных:

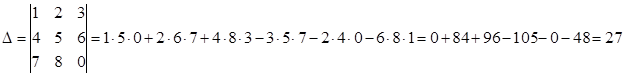Так как , то система имеет единственное решение.

Вычислим определители при неизвестных, подставляя столбец свободных членов вместо первого, второго и третьего столбцов определителя Δ:

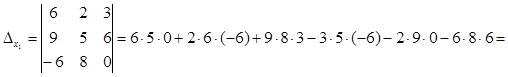
= 0 – 72 + 216 + = 90 – 0 – 288 = – 54;

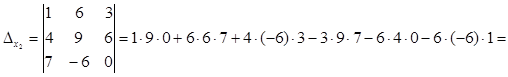
= 0 + 252 – 72 – 189 – 0 + 36 = 27;

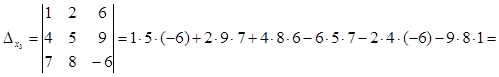
= – 30 + 126 + 192 – 210 + 48 – 72 = 54.

Найдем значения неизвестных по формулам Крамера:

Ответ. (–2; 1; 2).

2 б) Решить систему линейных уравнений методом Гаусса:

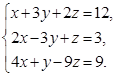
Решение. Составим расширенную матрицу системы:

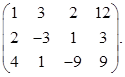
Для того чтобы получить и , вычтем из второй строки первую, умноженную на 2, а из третьей – первую, умноженную на 4:

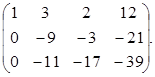
Чтобы получить , разделим вторую строку на (– 9):

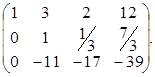
Чтобы получить , к третьей строке прибавим вторую, умноженную на 11:

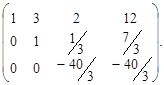
Запишем новую систему, которой соответствует полученная расширенная матрица:

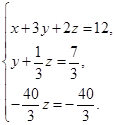
Выполняя обратный ход, найдем неизвестные: ;

Ответ. (4; 2; 1).

3. Вычислить пределы:

а)

Решение. При х = 1 числитель и знаменатель дроби равны нулю, имеем неопределенность вида о / о. Чтобы ее раскрыть, предварительно преобразуем данную дробь, разложив многочлены на множители:

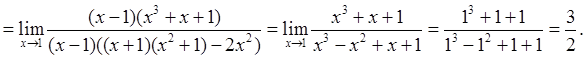
б)

Решение. Так как при х = 3 имеем неопределенность вида 0 / 0, то для вычисления предела разложим числитель и знаменатель дроби на множители:

х² – 5х + 6 = 0, D = 25 – 4∙6 = 1,

х² – 5х + 6 = (х – 3)(х – 2).

5х² – 5х – 30 = 0, D = 25 + 4∙5∙30 = 625,

5х² – 5х – 30 = 5(х – 3)(х + 2).

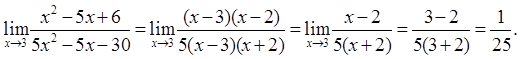
в)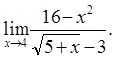

Решение. При х = 4 числитель и знаменатель дроби обращаются в нуль, имеем неопределенность вида 0 / 0. Чтобы ее раскрыть, умножим числитель и знаменатель на выражение, сопряженное знаменателю:

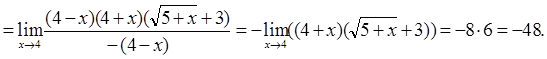
г)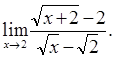

Решение. При х = 2 имеем неопределенность вида 0 / 0. Для того чтобы избавиться от нее умножим числитель и знаменатель дроби на сопряженные им выражения:

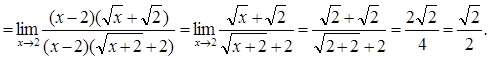
д)

Решение. Имеем неопределенность вида . Чтобы от нее избавиться разделим числитель и знаменатель дроби на наивысшую в данной дроби степень х, т.е. на :

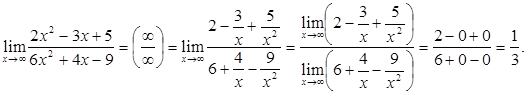
Здесь воспользовались тем, что при выражения , , , стремятся к нулю.

е)

Решение. Имеем неопределенность вида , поэтому разделим числитель и знаменатель на наивысшую степень х в данной дроби, а это х: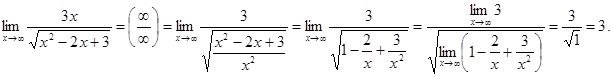

ж)

Решение. При х = 0 числитель и знаменатель дроби обращаются в нуль, имеем неопределенность вида 0 / 0. Чтобы от нее избавиться воспользуемся первым замечательным пределом .

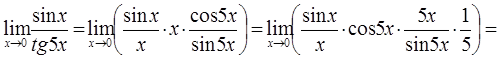
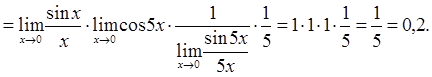
Так как при , то согласно первому замечательному пределу

з)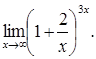

Решение. Здесь имеем неопределенность , для раскрытия которой воспользуемся вторым замечательным пределом

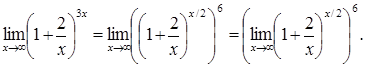
Пусть . Тогда при , поэтому, используя второй замечательный предел, получим

Итак,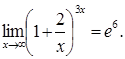

и)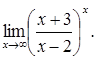

Решение. Поделив числитель и знаменатель дроби на х, сведем данный предел ко второму замечательному пределу

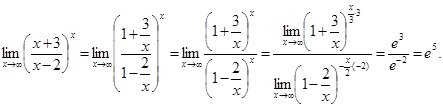
4.* Найти частные производные и полные дифференциалы первого и второго порядка функции

Решение. Сначала найдем частные производные первого порядка:

По формуле найдем полный дифференциал первого порядка функции:

Дифференцируя каждую из полученных функций по х и по у, получим частные производные второго порядка:

Как и следовало ожидать,

По формуле найдем полный дифференциал второго порядка функции:

5. Найти общее или частное решение дифференциального уравнения:

а) ;

б) , ;

в) , если у = 1, =5 при х = 0.

Решение. а) Это уравнение с разделяющимися переменными. Преобразуем его:

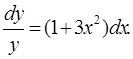
Проинтегрируем левую и правую части полученного уравнения:

Последнее выражение и является общим решением дифференциального уравнения. Найдем теперь его частное решение, удовлетворяющее условию :

С = 0.

Тогда частное решение дифференциального уравнения имеет вид

б) Преобразуем данное уравнение:

Получили уравнение с разделяющимися переменными. Для того чтобы разделить переменные, поделим обе части уравнения на , т.е. и , а затем проинтегрируем:

, ,

Для удобства потенцирования представим

, , , ,

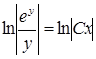Выражение , является общим интегралом данного дифференциального уравнения, а у=0 – его особое решение.

в) Это линейное однородное уравнение второго порядка с постоянными коэффициентами. Запишем характеристическое уравнение и решим его:

Поскольку характеристическое уравнение имеет комплексные корни, причем α = 3, β = 2, общее решение данного дифференциального уравнения имеет вид:

Дифференцируя общее решение, найдем у′:

Подставим теперь начальные данные в выражения для у и у′:

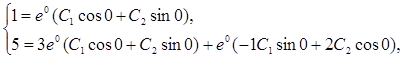
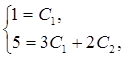
откуда и Таким образом, искомое частное решение имеет вид:

Учебно-методическое обеспечение

Основная учебная литература:

1. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 1: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 276 с. — (Профессиональное образование). — ISBN 978-5-534-10174-4. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442438

2. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 2: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 241 с. — (Профессиональное образование). — ISBN 978-5-534-10173-7. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442439

3. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440

4. Богомолов, Н. В. Математика: учебник для среднего профессионального образования / Н. В. Богомолов, П. И. Самойленко. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2021. — 401 с. — (Профессиональное образование). — ISBN 978-5-534-07878-7. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/449006

Дополнительная учебная литература:

1. Выгодский М. Я. Справочник по элементарной математике. – М.: АСТ, 2022. – 512 с.

2. Кремер Н.Ш. Линейная алгебра: учебник и практикум для СПО/ Н.Ш. Кремер, М.Н. Фридман, И.М. Тришин.; под ред. М.Ш. Кремера. – 3-е изд., испр. и доп. — М.: Издательство Юрайт, 2022. — 422 с. — (Серия: Профессиональное образование). Режим доступа: https://urait.ru/viewer/lineynaya-algebra.

3. Башмаков М. И. Математика: учеб. для студ. учреждений сред. проф. образования/ М. И. Башмаков. - 5-е изд., стер. - М.: Издательский центр "Академия", 2021. - 256 с.

4. Математика: учебник / А.А. Дадаян. — 3-е изд., испр. и доп. — Москва: ИНФРА-М, 2022. — 544 с. — (Cреднее профессиональное образование). - Текст: электронный. - URL: https://new.znanium.com/catalog/product/1006658

5. Стеклов, В. А. Математика и ее значение для человечества / В. А. Стеклов. — Москва: Издательство Юрайт, 2023. — 204 с. — (Антология мысли). — ISBN 978-5-534-08325-5. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/438600

6. Высшая математика: учебник и практикум для среднего профессионального образования / М. Б. Хрипунова [и др.]; под общей редакцией М. Б. Хрипуновой, И. И. Цыганок. — Москва: Издательство Юрайт, 2023. — 472 с. — (Профессиональное образование). — ISBN 978-5-534-01497-6. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/437476

Современные профессиональные базы данных и информационные ресурсы сети «Интернет»:

1. https://cfuv.ru/sveden/objects.

2. Издательство «Лань» - Режим доступа: https://e.lanbook.com

3. https://www.biblio-online.ru/–ЭБС Образовательная платформа Юрайт

4. Электронный ресурс «ГРАМОТА.РУ». Форма доступа: www.gramota.ru

5. Электронный каталог Библиотеки МосГУ IPRbooks. Электронно-библиотечная система KNIGAFUND.RU. Форма доступа: http://elib.mosgu.ru

6. Формулы, уравнения, теоремы, примеры решения задач. Форма доступа: http://matematika.electrichelp.ru/matricy-i-opredeliteli/

7. Материалы по математике для самостоятельной подготовки. Форма доступа: http://www.mathprofi.ru/

8. Изучение математики онлайн. Форма доступа: https://ru.onlinemschool.com/math/library/

9. Справочный портал. Форма доступа: https://www.calc.ru/

10. Информационные, тренировочные и контрольные материалы. Форма доступа: http://fcior.edu.ru/

11. Новая электронная библиотека. Форма доступа: http://www.newlibrary.ru/

12. Общероссийский математический портал. Форма доступа: http://www.mathnet.ru/

13. Научная электронная библиотека. Форма доступа: https://elibrary.ru/defaultx.asp

Скачано с www.znanio.ru

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

Пояснительная записка Цели и задачи учебной дисциплины – требования к результатам освоения дисциплины:

З 1 . А ктуальный профессиональный и социальный контекст, в котором приходится работать и жить;

Инструкционные карты к практическим занятиям

Задание 4. Вычислить определители третьего порядка методом треугольников: a ) , b ) , c )

Совместные и несовместные, определенные и неопределенные системы линейных уравнений

Понятие минора и алгебраических дополнений для матрицы

Ответить на контрольные теоретические вопросы

У 14 . Оценивать практическую значимость результатов поиска;

Частные производные функции нескольких переменных

Перечислите свойства неопределенного интеграла

Используя метод интегрирования по частям, вычислить следующие интегралы: а) ; б) ; в) ; г) ; д) ; е)

Задание 2. Используя метод замены переменной, вычислить следующие определенные интегралы: 1

З 5 . Структуру плана для решения задач;

Контрольная работа должна быть выполнена в срок, соответствующий учебному графику

Найти частные производные и полные дифференциалы первого и второго порядка для данной функции:

Пример варианта № 0 контрольной работы 1

Выполняя обратный ход, найдем неизвестные: ;

Пусть . Тогда при , поэтому, используя второй замечательный предел, получим

По формуле найдем полный дифференциал второго порядка функции: 5

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также