
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ СВЕРДЛОВСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СВЕРДЛОВСКОЙ ОБЛАСТИ
«ПЕРВОУРАЛЬСКИЙ МЕТАЛЛУРГИЧЕСКИЙ КОЛЛЕДЖ»
|
УТВЕРЖДЕНО Учебно-методическим объединением Протокол от «24» октября 2023 г. №35
|
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ
ЕН 01. Элементы высшей математики
для специальности среднего профессионального образования
09.02.07 Информационные системы и программирование
|
ПРИНЯТО |
|
Методическим советом колледжа Протокол от «31» октября 2023 г. №31
|
2023 г.
Составители: Фунтова Н.В.– преподаватели ГАПОУ СО «Первоуральский металлургический колледж»
Методические рекомендации по выполнению практических работ являются частью основной профессиональной образовательной программы по специальностям СПО 22.02.05 Обработка металлов давлением в соответствии с требованиями ФГОС.
Методические рекомендации по выполнению практических работ подготовлены на основании рабочей программы по специальностям СПО 22.02.05 Обработка металлов давлением студентам очной формы обучения.
Методические рекомендации включают в себя учебную цель, перечень образовательных результатов, заявленных в ФГОС СПО, задачи, обеспеченность занятия, краткие теоретические и учебно-методические материалы по теме, задания для практической работы студентов и инструкцию по ее выполнению.
СОДЕРЖАНИЕ
|
№ п/п |
Название практических работ |
страницы |
|
ПЗ1 |
Арифметические действия над числами, нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной), сравнение числовых выражений. Практические приемы вычислений. Действия с дробями (обыкновенными, десятичными, смешанными). Решение задач на пропорции, проценты |
6 |
|
ПЗ2 |
Действия над комплексными числами |
9 |
|
ПЗ3 |
Степень с произвольным показателем |
12 |
|
ПЗ4 |
Тождественные преобразования алгебраических выражений |
15 |
|
ПЗ5 |
Решение квадратных уравнений. Система двух уравнений с двумя неизвестными |
19 |
|
ПЗ6 |
Иррациональные уравнения. Дробно-рациональные неравенства, системы неравенств. |
19 |
|
ПЗ7 |
Свойства функции |
22 |
|
ПЗ8 |
Построение графика функции |
22 |
|
ПЗ9 |
Решение показательных уравнений и систем показательных уравнений |
25 |
|
ПЗ10 |
Решение показательных неравенств и систем показательных неравенств |
25 |
|
ПЗ11 |
Решение логарифмических уравнений и неравенств |
27 |
|
ПЗ12 |
Решение задач на параллельность прямых и плоскостей в пространстве |
30 |
|
ПЗ13 |
Нахождение углов между прямой и плоскостью |
30 |
|
ПЗ14 |
Параллельное и ортогональное проектирования и их свойства |
34 |
|
ПЗ15 |
Изображение пространственных фигур |
36 |
|
ПЗ16 |
Линейные операции над векторами (правила треугольника, параллелограмма, многоугольника) |
38 |
|
ПЗ17 |
Действия с векторами, заданными своими координатами |
40 |
|
ПЗ18 |
Вычисление тригонометрических функций |
42 |
|
ПЗ19 |
Тождественные преобразования тригонометрических функций |
45 |
|
ПЗ20 |
Решение тригонометрических уравнения общего вида |
47 |
|
ПЗ21 |
Решение тригонометрических неравенств |
51 |
|
ПЗ22 |
Вычисление предела числовой последовательности |
53 |
|
ПЗ23 |
Техника дифференцирования функций |
55 |
|
ПЗ24 |
Составление уравнения касательной к графику функции |
55 |
|
ПЗ25 |
Исследование функции и построение её графика с помощью с производной |
58 |
|
ПЗ26 |
Решение задач на связь первообразной и её производной |
60 |
|
ПЗ27 |
Вычисление неопределённого и определённого интегралов |
63 |
|
ПЗ28 |
Применение интеграла к вычислению физических величин и площадей плоских фигур |
65 |
|
ПЗ29 |
Решение задач на вычисление площадей плоских фигур с применением соответствующих формул и фактов из планиметрии |
68 |
|
ПЗ30 |
Построение сечений, разверток многогранников. Нахождение основных элементов многогранников |
71 |
|
ПЗ31 |
Вычисление площадей поверхностей и объемов многогранников |
73 |
|
ПЗ32 |
Изображение тел вращения, их развертки, сечений. Нахождение основных элементов цилиндра, конуса, шара |
75 |
|
ПЗ33 |
Вычисление площадей поверхностей и объемов тел вращения |
77 |
|
ПЗ34 |
Решение прикладных задач с использованием понятий и правил комбинаторики |
79 |
|
ПЗ35 |
Биноминальное разложение с использованием треугольника Паскаля |
79 |
|
ПЗ36 |
Решение задач на вычисление вероятности события |
81 |
|
ПЗ37 |
Решение прикладных задач с применением вероятностных методов |
81 |
|
ПЗ38 |
Графическое представление числовых данных: таблицы, диаграммы, графики. Знакомство со встроенными функциями Exsel для нахождения основных характеристик выборки. Решение задач на выборку: графическое представление и нахождение основных характеристик |
84 |
|
ПЗ39 |
Итоговое повторение. |
87 |
|
|
Приложение 1 |
90 |
Введение
УВАЖАЕМЫЙ СТУДЕНТ!
Методические рекомендации по дисциплине ОДП.10 Математика для выполнения практических работ созданы Вам в помощь для работы на занятиях, подготовки к практическим работам.
Приступая к выполнению практической работы, Вы должны внимательно прочитать цель и задачи занятия, ознакомиться с требованиями к уровню Вашей подготовки в соответствии с федеральными государственными стандартами, краткими теоретическими и учебно-методическими материалами по теме практической работы.
Наличие положительной оценки по практическим работам необходимо для получения допуска к экзамену по дисциплине, поэтому в случае отсутствия на уроке по любой причине или получения неудовлетворительной оценки за практическую работу Вы должны найти время для ее выполнения или пересдачи.
Внимание! Если в процессе подготовки к практическим работам или при решении задач у Вас возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий.
Время проведения дополнительных занятий можно узнать у преподавателя.
Желаем Вам успехов!!!
|
Раздел 1 |
Алгебра. Уравнения и неравенства алгебраические |
|
|
Тема 1.1 |
Развитие понятия о числе |
|
Практическое занятие №1. Арифметические действия над числами, нахождение приближенных значений величин и погрешностей вычислений (абсолютной и относительной), сравнение числовых выражений. Практические приемы вычислений. Действия с дробями (обыкновенными, десятичными, смешанными). Решение задач на пропорции, проценты
Учебная цель: Применение правил действия с приближёнными числами к решению задач.
Учебные задачи:
1. Закрепить навык действий над числами.
2. Научиться вычислять погрешность
3. Научиться решать задачи с составлением пропорции.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Если х - точное значение числа,
а – приближённое значение, то х ≈ а.
ОПР.
Разность х – а между точным и приближённым значением числа называется погрешностью приближения.
ОПР.
Модуль разности между точным и приближённым значением числа называется абсолютной погрешностью приближения ∆а = │х – а│.
ОПР.
Некоторая цифра приближённого числа считается верной, если его абсолютная погрешность
∆а не превышает единицы того разряда, в котором стоит эта цифра. В противном случае цифра называется сомнительной.
Пример.
а = 945,673 ± 0,03
6 – цифра десятых долей, ∆а = 0,03
Проверяем: 0,03 < 0,1 – верное неравенство, значит 6 – верная цифра. Цифры, стоящие перед 6 тоже верные.
7 – цифра сотых долей
Проверяем: 0,03 < 0,01 – нет, значит 7 – сомнительная цифра.
ОПР.
Значащими цифрами десятичной дроби называют все её цифры, кроме нулей, расположенных левее первой, отличной от нуля цифры
ОПР.
Значащими цифрами целого числа называют все его цифры, кроме нулей, расположенных в конце числа, если они стоят взамен неизвестных или отброшенных цифр.
0,712 - 3 значащие цифры.
45,03 – 4 значащие цифры
0,0016 - 2 значащие цифры
ОПР.
Относительной погрешностью приближённого значения числа а называется отношение абсолютной погрешности этого числа к модулю приближённого значения.
Ϭ = ∆а * 100%
│а│
Правила подсчёта цифр:
1. При сложении и вычитании приближённых чисел в результате сохраняют столько десятичных знаков, сколько их в наименее точном числе.
2. При умножении и делении приближённых чисел в результате сохраняют столько значащих цифр, сколько их в числе с наименьшим количеством значащих цифр.
3. При возведении в степень в результате сохраняют столько значащих цифр, сколько их в основании степени.
4. При извлечении корня сохраняют столько значащих цифр, сколько их в подкоренном выражении.
5. При выполнении промежуточных действий оставляют на один знак больше, чем требуют правила, а в результате запасной знак округляют.
6. Если в вычислениях точность задана заранее, то вычисления ведут с запасным знаком, который в результате округляют
Задачи практической работы:
1 вариант.
1 задание. Установить число значащих цифр в числе: а) 649 ; б) 0,01405; в) 347|51≈ ; г) 24321≈
2 задание. Определить верные и сомнительные цифры чисел
а) а = 85,263 ± 0,0084 б) х = 729,3 ± 1
3 задание. Вычислить значение выражений с оценкой погрешностей, если все числа даны с верными
цифрами.
а) 645,27 + 102,234 + 715,645 + 10,2 б) 96,891 – 4,25
33,3 + 0,426
4 задание. Округлить число до единиц и найти абсолютную и относительную погрешности
приближения : 23,263
2 вариант.
1 задание. Установить число значащих цифр в числе: а) 43,08; б) 0,0298 ; в) 353|617≈ ; г) 25|213 ≈
2 задание. Определить верные и сомнительные цифры чисел
а) х = 14,28 ± 0,05 б) а = 749,3 ± 1
3 задание. Вычислить значение выражений с оценкой погрешностей, если все числа даны с верными цифрами.
а) 12030 + 645,29 + 748,5 + 1625,375 б) ( 0,17 + 0,2445 ) · 0, 56
1,424
4 задание. Округлить число до единиц и найти абсолютную и относительную погрешности Приближения: 0,892
3 вариант.
1 задание. Установить число значащих цифр в числе: а) 0,39 ; б) 5,0300 ; в) 347|51≈ ; г) 24|321≈
2 задание. Определить верные и сомнительные цифры чисел
а) х = 729,5 ± 1 б) а = 679,3 ± 0,06
3 задание. Вычислить значение выражений с оценкой погрешностей, если все числа даны с верными цифрами.
а) 26,35 + 1400 + 729,3 + 745,68 б) 37,2 + 458.67
36,5 + 246
4 задание. Округлить число до единиц и найти абсолютную и относительную погрешности приближения : 23,263
4 вариант.
1 задание. Установить число значащих цифр в числе: а) 0,0016; б) 305,7; в)353|617≈ ; г) 25|213≈
2 задание. Определить верные и сомнительные цифры чисел
а) а = 14,28 ± 0,03 б) х = 15,365 ± 0,002
3 задание. Вычислить значение выражений с оценкой погрешностей, если все числа даны с верными цифрами.
а) 15,283 + 4,04527 +8,253471 + 17,52 б) 96,891 – 4,25
33,3 + 0,426
4 задание. Округлить число до единиц и найти абсолютную и относительную погрешности приближения : 0,892
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 1 |
Алгебра. Уравнения и неравенства алгебраические |
|
|
Тема 1.1 |
Развитие понятия о числе |
|
Практическое занятие №2. Действия над комплексными числами
Учебная цель: Применение правил действия с комплексными числами.
Учебные задачи:
1. Закрепить навык действий над комплексными числами.
2. Научиться решать уравнения с комплексной переменной.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
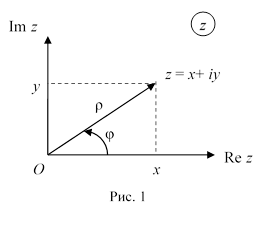 Комплексное число – это
число, состоящее из действительной и мнимой частей. Комплексное
число
Комплексное число – это
число, состоящее из действительной и мнимой частей. Комплексное
число ![]() может быть
представлено в различных формах:
может быть
представлено в различных формах:
·
алгебраической: ![]() ;
;
· геометрической (рис.1):
· тригонометрической:
![]() ,
,
![]() ;
;
·
показательной: ![]() .
.
Обозначения:
![]() – действительная часть числа
– действительная часть числа ![]() ,
, ![]() ;
;
![]() –
мнимая часть числа
–
мнимая часть числа ![]() ,
, ![]() ;
;
![]() –
мнимая единица,
–
мнимая единица, ![]() ;
;
![]() –
модуль числа
–
модуль числа ![]() ;
;
φ – аргумент числа ![]() .
.
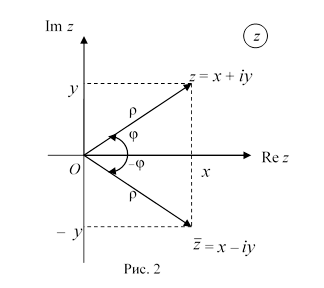
Наряду с
комплексным числом
z = х + i y рассмотрим
число ![]() = х – i y, которое называют
сопряженным числу z (рис.2).
= х – i y, которое называют
сопряженным числу z (рис.2).
Найдем z • ![]() :
:
z • ![]() =
(х + i y ) (х – i y) = х 2
– i2 y
2 = х 2 + y 2 = | z | 2.
=
(х + i y ) (х – i y) = х 2
– i2 y
2 = х 2 + y 2 = | z | 2.
Для того, чтобы перевести
алгебраическую форму комплексного числа ![]() в
тригонометрическую и показательную формы, необходимо найти φ – аргумент
числа
в
тригонометрическую и показательную формы, необходимо найти φ – аргумент
числа ![]() .
.
φ* = arg z, –π < φ* ≤ π.
(Иногда главное значение аргумента z заключают в пределах от 0 (включая 0) до 2π: 0 ≤ φ* < 2π).
φ = Arg z = φ*+ 2πk
= arg z
+ 2πk, k ![]() Z.
Z.
φ*=
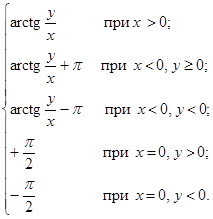
Если x = 0 и y = 0, т. е. для z = 0, аргумент z не определен.
В поле комплексных чисел имеет место формула Эйлера:
![]() = cos φ + i sin φ.
= cos φ + i sin φ.
С помощью этой формулы можно от тригонометрической формы комплексного числа перейти к показательной его форме:
z = x + iy
= ρ(cos φ + i sin φ) = ρ![]() .
.
Итак, комплексное число может быть представлено в
алгебраической, тригонометрической и показательной формах:
z = x + iy = ρ(cos φ + i sin φ) = ρ![]() .
.
Тригонометрическая и показательная формы комплексного числа удобны при перемножении комплексных чисел, а также при возведении их в натуральную степень или извлечении корня натуральной степени из комплексного числа.
Операции над комплексными числами
Сложение и вычитание комплексных чисел ![]() и
и ![]() удобно
выполнять в алгебраической форме:
удобно
выполнять в алгебраической форме:
|
|
|
Для выполнения умножения и деления удобна любая форма
Задачи практической работы:
Задача 1. Найти действительную и мнимую часть чисел ![]() , если
, если
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
6. ![]() .
.
7. ![]() .
.
8. ![]() .
.
9. ![]() .
.
10.![]()
Результаты вычислений изобразить в координатной плоскости.
Задачи 2. Решить квадратное уравнение.
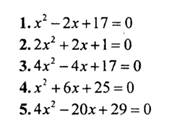
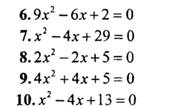
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 1 |
Алгебра. Уравнения и неравенства алгебраические |
|
|
Тема 1.2 |
Корни и степени. Преобразование алгебраических выражений. |
|
Практическое занятие №3. Степень с произвольным показателем
Учебная цель: Применение правил действия при преобразованиях степенных выражений.
Учебные задачи:
1. Закрепить навык действий над степенями с произвольным показателем.
2. Научиться упрощать выражения, содержащие степень.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр.
Если п – натуральное число, т – целое
число и частное ![]()
![]() является целым числом, то при а
> 0 справедливо равенство
является целым числом, то при а
> 0 справедливо равенство ![]()
Пример
![]()
Опр.
Для любых рациональных чисел p и q и а >0 и b >0 верны равенства:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. Если а ≠ 0 , то а 0 = 1
Пример
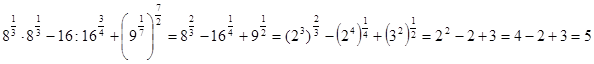
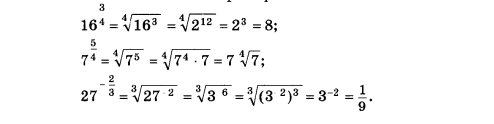
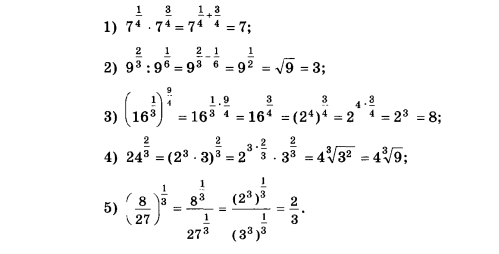


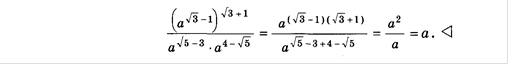
Задачи практической работы:
1 вариант
1. Вычислить: а) ![]()
![]()
![]() ;
б)
;
б) 
2. Упростить выражение: а) ![]() ; б)
; б) ![]() ;
;
3. Вычислить: а) ![]() ;
б)
;
б) ![]() ;
;
в) 
4. Упростить выражение: ![]()
5. Упростить выражение: а) ![]() б)
б) ![]()
2 вариант
1. Вычислить: а) ![]()
![]() б)
б) 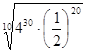
2. Упростить выражение: ; а) ![]() ; б)
; б) ![]()
3. Вычислить: а)![]() ; б)
; б)![]() ;
;
в) ![]()
4. Упростить выражение: ![]()
5. Упростить выражение: а) ![]() ; б)
; б) 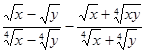
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 1 |
Алгебра. Уравнения и неравенства алгебраические |
|
|
Тема 1.2 |
Корни и степени. Преобразование алгебраических выражений. |
|
Практическое занятие №4. Тождественные преобразования алгебраических выражений.
Учебная цель: Применение правил действия при преобразованиях степенных выражений.
Учебные задачи:
1. Закрепить навык действий над степенями с произвольным показателем.
2. Научиться выполнять тождественные преобразования алгебраических выражений.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр.
Если п – натуральное число, т – целое
число и частное ![]()
![]() является целым числом, то при а
> 0 справедливо равенство
является целым числом, то при а
> 0 справедливо равенство ![]()
Пример
![]()
Опр.
Для любых рациональных чисел p и q и а >0 и b >0 верны равенства:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. Если а ≠ 0 , то а 0 = 1
Пример
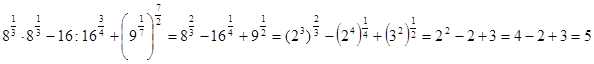
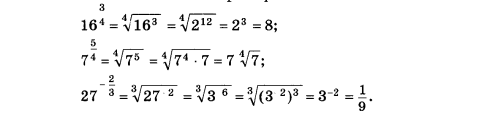
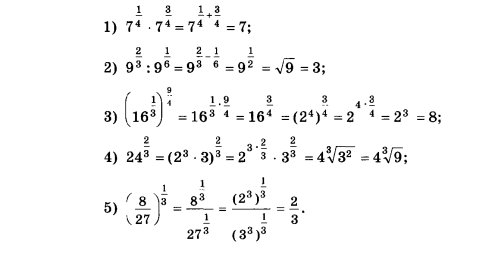
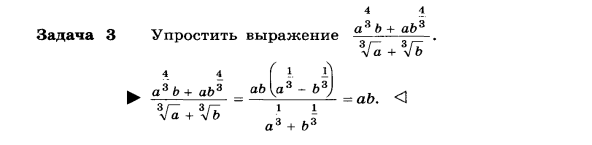

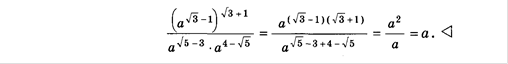
Опр.
Арифметическим корнем натуральной степени п ≥ 2 из неотрицательного числа а называется
неотрицательное число, п – ая степень которого равна а.
Примеры
1. ![]() , так как 4 > 0 и 43 =
64 2.
, так как 4 > 0 и 43 =
64 2. ![]() , так как 5 > 0 и 53
= 125
, так как 5 > 0 и 53
= 125
Из определения арифметического
корня следует, что если а ≥ 0, то ![]() и
и ![]()
Свойства арифметического корня:
Арифметический корень п – ой степени обладает следующими свойствами: если а ≥ 0, b ≥ 0 и п, т - натуральные числа, причём п ≥ 2 , т ≥ 2 , то
1. ![]() 2.
2.
![]()
3. ![]() 4.
4.
![]()
Корень нечётной степени из отрицательного числа а вычисляется следующим образом:
![]()
Например, ![]()
Примеры применения свойств арифметического корня.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()

Задачи практической работы:
Практическая работа №4
1 вариант
1. Вычислить: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
г)
;
г) 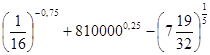
2. Представить в виде
степени с рациональным показателем:
а) ![]() ; б)
; б) ![]() ;
;
3. Вычислить: а) ![]() ; б)
; б) ![]() ;
;
4. Сравнить числа: а)![]() или
или
![]() ; б)
; б)![]() или
или
![]() ; в)
; в) ![]() или
или
![]() г)
г) 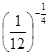 или
или
![]()
5. Упростить
выражение: а) 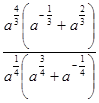 ; б)
; б) 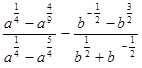
2 вариант
1. Вычислить: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
2. Представить в виде
степени с рациональным показателем:
а) ![]() ; б)
; б) ![]()
3. Вычислить: а) ![]() ; б)
; б) ![]() ;
;
4. Сравнить числа: а)![]() или
или
![]() б)
б)![]() или
или
![]() ; в)
; в) ![]() или
или
![]() г)
г) 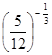 или
или
![]()
5. Упростить
выражение: а) 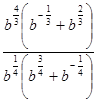 ;
б)
;
б) 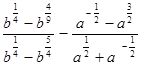
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
Раздел 1 |
Алгебра. Уравнения и неравенства алгебраические |
|
|
Тема 1.3 |
Уравнения и неравенства алгебраические. |
|
Практическое занятие №5. Решение квадратных уравнений. Система двух уравнений с двумя неизвестными.
Практическое занятие №6. Иррациональные уравнения. Дробно-рациональные неравенства, системы неравенств.
Учебная цель: Применение правил действия при решении алгебраических уравнений и неравенств.
Учебные задачи:
1. Закрепить навык действий при решении уравнений и неравенств.
2. Научиться решать системы уравнений тремя методами.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Определение. Квадратное уравнение – это уравнение вида ax2 + bx + c = 0,
где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Основная формула корней квадратного уравнения
![]()
Определение. Системой двух уравнений с двумя неизвестными x и y называется пара уравнений с двумя неизвестными:
![]()
Определение. Пара чисел ![]() называется
решением системы, если подстановка этих чисел вместо соответствующих
неизвестных обращает каждое уравнение в верное числовое равенство.
называется
решением системы, если подстановка этих чисел вместо соответствующих
неизвестных обращает каждое уравнение в верное числовое равенство.
Определение. Решить систему – значит найти все ее решения или доказать, что их нет.
Методы решения систем: метод подстановки, метод сложения, графический метод, метод введения новых переменных.
Задачи практической работы:
Практическая работа № 5
Вариант 1
1. Решить уравнение:
![]()
2. Составить квадратное уравнение, если известны корни:
![]()
3. Решить уравнение:
![]()
4. Решите
уравнение: а) ![]() б)
б) ![]() .
.
5. Решить
неравенство ![]()
Вариант 2
1. Решить уравнение:
![]()
2. Составить квадратное уравнение, если известны корни:
![]()
3. Решить уравнение:
![]()
4. Решите
уравнение: а) ![]() б)
б) ![]() .
.
5. Решить
неравенство ![]()
Практическая работа № 6
Вариант 1
1. Решить систему уравнений: а) 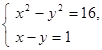 б)
б) 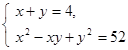
2. Решить систему неравенств: ![]()
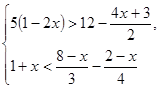
3. Решить графически систему уравнений: 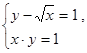
4. Решить графически систему неравенств: 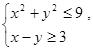
Вариант 2
1. Решить систему уравнений: а) 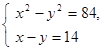 б)
б) 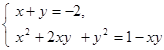
2. Решить систему неравенств: ![]()
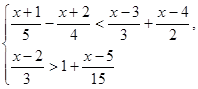
3. Решить графически систему уравнений: 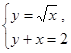
4. Решить графически систему неравенств: 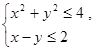
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 2 |
Функции, их свойства и графики. Уравнения и неравенства показательные и логарифмические |
|
|
Тема 2.1 |
Функции, их свойства и графики |
|
Практическое занятие №5. Свойства функции
Практическое занятие №6. Построение графика функции
Учебная цель: Построение и анализ графика функции.
Учебные задачи:
1. Научиться строить график заданной функции различными способами.
2. Научиться анализировать график заданной функции.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Если каждому
значению х из некоторого числового множества Х ставится по
определенному правилу f единственное значение у
из числового множества У, то говорят, что задана функция на
множестве Х и записывают ![]() .
.
Переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной. Число у, соответствующее заданному значению х, называется значением функции в точке х. Множество Х (обозначают D(у)) – область определения функции, множество У (обозначают E(у))– множество значений функции.
Основные элементарные функции
1. Степенные
функции: ![]() .
.
2. Показательные
функции: ![]() .
.
3. Логарифмические
функции: ![]() .
.
4. Тригонометрические
функции: ![]() .
.
5. Обратные
тригонометрические функции ![]() ,
, ![]() .
.
Функция может быть задана таблицей, формулой, графиком.
Графики некоторых функций приведены в таблице 1.
Свойства функций
1. Четность (нечетность).
Функция ![]() , заданная на симметричном
относительно начала координат промежутке, называется
, заданная на симметричном
относительно начала координат промежутке, называется
·
четной, если для любого значения х из этого
промежутка выполняется равенство ![]() ;
;
·
нечетной, если для любого значения х из этого
промежутка выполняется равенство ![]() .
.
График четной функции симметричен относительно оси ординат (например, ![]() ), а график нечетной функции –
относительно начала координат (например,
), а график нечетной функции –
относительно начала координат (например, ![]() ).
).
2. Монотонность.
Пусть функция
определена на множестве D и пусть множество ![]() .
.
Функция ![]() называется возрастающей
(убывающей) на данном промежутке А, если для любых
называется возрастающей
(убывающей) на данном промежутке А, если для любых ![]() , таких, что
, таких, что ![]() выполняется неравенство
выполняется неравенство ![]() (
(![]() ).
).
Например, функция ![]() убывает на
промежутке
убывает на
промежутке ![]() и возрастает на промежутке
и возрастает на промежутке ![]()
![]() .
.
3. Периодичность.
Функция ![]() называется периодической,
если существует такое отличное от нуля число Т, что для любого х
из области определения D функции значение
называется периодической,
если существует такое отличное от нуля число Т, что для любого х
из области определения D функции значение ![]() и выполняется равенство
и выполняется равенство ![]() . Число Т называется периодом функции.
. Число Т называется периодом функции.
Если Т
– период функции, то ее периодами будут также числа ![]() ,
где
,
где ![]() . Наименьший положительный период
называется основным периодом функции.
. Наименьший положительный период
называется основным периодом функции.
Периодическими
являются тригонометрические функции. Число ![]() является
основным периодом функций
является
основным периодом функций ![]() и
и ![]() , а основным периодом функций
, а основным периодом функций ![]() и
и ![]() является
является
![]() .
.
Задачи практической работы:
Практическая работа № 7
Вариант 1
1. Найдите область определения функции:
а) ![]() ;
б)
;
б) ![]()
2. Найдите функцию,
обратную данной, ее область определения и множество значений: ![]() .
.
Вариант № 2
1. Найдите область определения функции:
а) ![]() ;
б)
;
б) ![]()
2. Найдите функцию,
обратную данной, ее область определения и множество значений: ![]() .
.
Вариант № 3
1. Найдите область определения функции:
а) ![]() б)
б) ![]()
2. Найдите функцию,
обратную данной, ее область определения и множество значений: ![]() .
.
Вариант № 4
1. Найдите область определения функции:
а) ![]() б)
б) ![]()
2. Найдите функцию,
обратную данной, ее область определения и множество значений: ![]() .
.
Практическая работа № 8
Вариант 1
Постройте график функции. Найдите ее область определения и множество значений.
1. y = x2 – 2x +3
2. ![]()
Вариант 2
Постройте график функции. Найдите ее область определения и множество значений.
1. y = x2 + 3x - 5
2. ![]()
Вариант 3
Постройте график функции. Найдите ее область определения и множество значений.
1. y = x2 – x + 4
2. ![]()
Вариант 4
Постройте график функции. Найдите ее область определения и множество значений.
1. y = x2 – 2x +1
2. ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 2 |
Функции, их свойства и графики. Уравнения и неравенства показательные и логарифмические |
|
|
Тема 2.2 |
Показательные и логарифмические функции, уравнения и неравенства |
|
Практическое занятие №9. Решение показательных уравнений и систем показательных уравнений
Практическое занятие №10. Решение показательных неравенств и систем показательных неравенств
Учебная цель: Применение знаний при решении показательных уравнений и неравенств и их систем.
Учебные задачи:
1. Научиться решать показательные уравнения и неравенства..
2. Систематизировать знания по решению систем показательных уравнений и неравенств.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр.
Показательными уравнениями называются уравнения, в которых неизвестное содержится в показателе степени.
1) Простейшие уравнения, т.е. такие, левую и правую части которых можно привести к одному основанию решаются так:
Пример
![]()
![]()
2) Уравнения вида ![]() решаются вынесением за скобки
степени с наименьшим показателем.
решаются вынесением за скобки
степени с наименьшим показателем.
3) Уравнения, вида ![]() решаются с помощью подстановки ах
= у , сводится к квадратному.
решаются с помощью подстановки ах
= у , сводится к квадратному.
Пример
Решить уравнение: 52x + 1 – 26 • 5x + 5 = 0
Решение:
5x = y,
5y2 – 26y
+ 5 = 0,
D = 169 – 25 = 144,
y1 = 5 y2
= 1/5
5x =
5
x – 1,
5x =
1/5
x = – 1
Ответ: x = 1 и x = –1
4) При решения
уравнения вида ![]() обе части уравнения
необходимо разделить на
обе части уравнения
необходимо разделить на ![]() , т.к.
, т.к. ![]() ≠ 0
≠ 0
![]() .
.
Решение показательных неравенств сводится к решению
простейших неравенств вида ![]() b
b
или ![]()
Если а > 1 и ![]() b, то х > b
b, то х > b
Если 0 < a <
1 и ![]() b
, то x < b
b
, то x < b
Пример Решить неравенство: ![]()
Решение:
5(4–x)/2 > 5–3, а = 5, сравним показатели (4 – х)/2 > –3, 4 – х > –6, –х > –10, х < 10
Ответ: х < 10
Задачи практической работы:
Практические работы №9-10
1 вариант
1. Решить уравнение:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]()
г) ![]() ; д)
; д) ![]()
2. Решить неравенство:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д)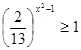 .
.
3. Решите систему уравнений: ![]()
2 вариант
1. Решить уравнение:
а) ![]() ; б)
; б) ![]() ; в)
; в) 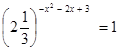
г) ![]() ; д)
; д) ![]()
2. Решить неравенство:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() <
12 ; г)
<
12 ; г) ![]() ; д)
; д) 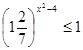 .
.
3. Решите систему
уравнений: ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 2 |
Функции, их свойства и графики. Уравнения и неравенства показательные и логарифмические |
|
|
Тема 2.2 |
Показательные и логарифмические функции, уравнения и неравенства |
|
Практическое занятие №11. Решение логарифмических уравнений и неравенств
Учебная цель: Применение знаний при решении логарифмических уравнений и неравенств.
Учебные задачи:
1. Знать основные свойства логарифмов.
2. Уметь выполнять тождественные преобразования логарифмических выражений.
3. Научиться решать логарифмические уравнения и неравенства..
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр.
Логарифмом числа b по основанию а, где а > 0 , а ≠ 1, называется показатель степени, в которую надо возвести число а, чтобы получить число b.
Примеры
1. ![]()
![]()
2. ![]()
Определение логарифма можно
записать так ![]() . Его называют основным
логарифмическим тождеством.
. Его называют основным
логарифмическим тождеством.
При преобразовании и вычислении значений логарифмических выражений применяют свойства логарифмов.
Свойства
1. ![]()
2. ![]()
3. ![]()
4. 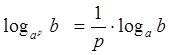
Формула перехода к другому основанию: ![]()
Опр.
Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b вместо log10 b
log10 b= lg b
Опр.
Натуральным логарифмом числа называют логарифм этого числа по основанию е, где е - иррациональное число, приближённо равное 2,7. При этом пишут ln b вместо loge b, т.е. loge b = ln b
Действие нахождения логарифма числа называется логарифмированием.
Действие, обратное логарифмированию называется потенцированием.
Примеры
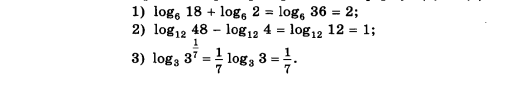
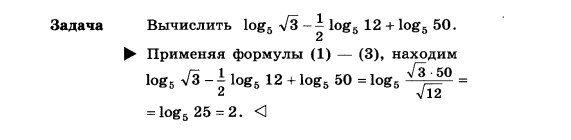
Задачи практической работы:
Практическая работа №11
Вариант № 1
1. Построить
график функции ![]() .
Как изменяется y, когда x возрастает от
.
Как изменяется y, когда x возрастает от ![]() до
8?
до
8?
2. Вычислить:
а) ![]() б)
б) ![]() в)
в) ![]()
3.
Сравнить числа: ![]()
4. Решить
уравнение: а) ![]() б)
б) ![]()
5. Решить
неравенство: ![]()
Вариант № 2
1. Построить
график функции ![]() .
Как изменяется y, когда x возрастает от
.
Как изменяется y, когда x возрастает от ![]() до
16?
до
16?
2.
Вычислить: а) ![]() б)
б) ![]() в)
в) ![]()
3.
Сравнить числа: ![]()
4. Решить
уравнение: а) ![]() б)
б) ![]()
5. Решить
неравенство: ![]()
Вариант № 3
1. Построить
график функции ![]() .
Как изменяется y, когда x возрастает от
.
Как изменяется y, когда x возрастает от ![]() до
4?
до
4?
2.
Вычислить: а) ![]() б)
б) ![]() в)
в) ![]()
3.
Сравнить числа: ![]()
4. Решить
уравнение: а) ![]() б)
б) ![]()
5. Решить
неравенство: ![]()
Вариант № 4
1. Построить
график функции ![]() .
Как изменяется y, когда x убывает от
.
Как изменяется y, когда x убывает от ![]() до
до ![]() ?
?
2. Вычислить:
а) ![]() б)
б) ![]() в)
в) ![]()
3. Сравнить
числа: ![]()
4. Решить
уравнение: а) ![]() б)
б) ![]()
5. Решить
неравенство: ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 3. |
Геометрия. Прямые и плоскости в пространстве. Координаты и векторы |
|
|
Тема 3.1 |
Прямые и плоскости в пространстве |
|
Практическое занятие №12. Решение задач на параллельность прямых и плоскостей в пространстве
Практическое занятие №13. Нахождение углов между прямой и плоскостью
Учебная цель: развитие пространственного воображения студентов при решении геометрических задач, развитие геометрического мышления.
Учебные задачи:
1. Уметь решать задачи на параллельность прямых и плоскостей в пространстве.
3. Уметь находить углы между прямой и плоскостью.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
![]()
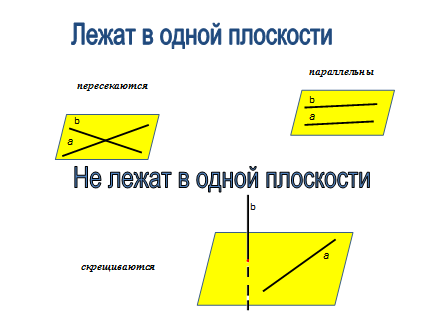

Определение
![]()
![]()

b ![]() α , с
║ α
α , с
║ α

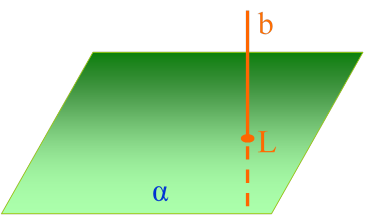
b ∩ α
![]()
![]()
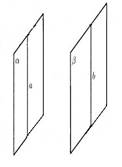

Опр. Две плоскости называются параллельными, если они не пересекаются
Задачи практической работы:
Практическая работа №12
1 вариант
1) Треугольники АВС и АДС лежат в разных плоскостях и имеют общую сторону АС. Точка
Р – середина стороны АД, точка К – середина ДС.
а) Каково взаимное расположение прямых РК и АВ?
б) Чему равен угол между прямыми РК и АВ, если угол АВС равен 40º, а угол ВСА = 80º. Ответ обобщите.
2) Прямые а и в лежат в параллельных плоскостях. Могут ли эти прямые быть
а) параллельными б) скрещивающимися? Сделать рисунок для каждого возможного случая.
3) Точка В не лежит в плоскости ∆ АДС. Точки М, N и Р – середины отрезков ВА, ВС, ВД соответственно. а) Доказать, что плоскости (MNP) и (АДС) параллельны; б) Найдите площадь треугольника MNP, если S∆АДС = 48 см2 .
2 вариант
1) Основание трапеции АВСД лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках E и F соответственно.
1) Каково взаимное расположение EF и АВ?
2) Чему равен угол между прямыми EF и АВ, если угол АВС = 150º. Ответ обоснуйте.
2) Прямые а и в лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть
а) параллельными б) скрещивающимися? Сделать рисунок для каждого случая.
3) В тетраэдре ДАВС точки M, N и P – середины рёбер ДА, ДВ, ДС соответственно.
а) Доказать, что плоскости (MNP) и (АВС) параллельны.
б) Найти площадь ∆ АВС, если S∆MNP = 14 см2 .
3 вариант
1) В тетраэдре АВСД точки М, К, Р являются серединами рёбер АВ, ВС, ВД. Доказать, что плоскость (МКР) параллельна плоскости (АДС) и вычислить S∆МКР , если S∆АДС = 48 см2 .
2) Прямая МК, не лежащая в плоскости АВС, параллельна стороне АВ параллелограмма АВСД. Выяснить взаимное расположение прямых МК и АД и найти угол между ними, если угол АДС = 130º.
3) В ромбе АВСД диагонали пересекаются в точке О, точка F не лежит в плоскости (АВС). Можно ли провести плоскость через FC и точки А и О? Ответ обоснуйте.
4 вариант
1) В тетраэдре ДАВС точки К, Е, М являются серединами рёбер АС, ДС, ВС. Доказать, что плоскость (КЕМ) параллельна плоскости (АДВ) и вычислить S∆АДВ , если S∆КЕМ = 27 см2 .
2) Прямая m параллельна диагонали ВД ромба АВСД и не лежит в плоскости ромба. Докажите, что m и АД – скрещивающиеся прямые – и найдите угол между ними, если угол АВС равен 128º.
3) Дан параллелограмм АВСД и точка Е, не лежащая в плоскости (АВС). Как расположена прямая АС и плоскость ЕВД? Ответ обоснуйте.
Практическая работа №13
1 вариант
1. Дан тетраэдр МАВС, в котором МВ ![]() ВА.
Доказать, что ∆МВД – прямоугольный, если Д – произвольная точка отрезка
АС. Найти МД и площадь ∆МВД, если
ВА.
Доказать, что ∆МВД – прямоугольный, если Д – произвольная точка отрезка
АС. Найти МД и площадь ∆МВД, если
МВ = ВД = а.
2. Из точки М проведён перпендикуляр МД = 6 см к плоскости квадрата. Наклонная МО образует с плоскостью квадрата угол 60º. О – точка пересечения диагоналей. Доказать, что ∆МОД – прямоугольный. Найти площадь квадрата.
2 вариант
1. Четырёхугольник АВСД – квадрат, О – его центр. Прямая ОМ перпендикулярна плоскости квадрата. Доказать, что МА = МВ = МС = МД. Найдите МА, если АВ = 4 см, ОМ = 1 см.
2. Из точки М проведён перпендикуляр к плоскости ∆АВС. ВМ = 9 см, АС = 10 см,
ВС = ВА = 13 см. Найдите расстояние от точки М до прямой АС.
3 вариант
1. Расстояние от точки М до каждой из вершин правильного треугольника АВС равна 4 см. Найти расстояние от точки М до плоскости треугольника АВС, если
АВ = 6 см.
2. Из точки М проведён перпендикуляр МВ = 4 см к плоскости прямоугольника АВСД. Наклонные МА и МС образуют с плоскостью прямоугольника углы 45º и 30º соответственно. Доказать, что ∆МАД и ∆МСД прямоугольные. Найти стороны прямоугольника.
4 вариант
1. Через вершину А прямоугольного треугольника АВС с прямым углом С проведена прямая АД, перпендикулярная к плоскости треугольника. Докажите, что
∆СВД – прямоугольный. Найти ВД, если ВС = 4, ДС = 5.
2. Через вершину В ромба АВСД проведена прямая ВМ,
перпендикулярная его плоскости. Найти расстояние от точки М до прямых,
содержащих стороны ромба. Если АВ = 25 см, ![]() ВАД
= 60º, ВМ = 12,5см.
ВАД
= 60º, ВМ = 12,5см.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 3. |
Геометрия. Прямые и плоскости в пространстве. Координаты и векторы |
|
|
Тема 3.1 |
Прямые и плоскости в пространстве |
|
Практическое занятие №14. Параллельное и ортогональное проектирования и их свойства
Учебная цель: развитие пространственного воображения студентов при решении геометрических задач, развитие геометрического мышления.
Учебные задачи:
1. Знать методы проектирования и их свойства.
2. Уметь решать задачи на параллельный перенос и симметрию относительно плоскости.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
При решении задач на движение пространства, надо знать виды движения. Это центральная симметрия, осевая симметрия, зеркальная симметрия и параллельный перенос.
Опр. (центральная симметрия)
Точки М и М1 называются симметричными относительно т О (центр симметрии), если О – середина отрезка ММ1. Точка О считается симметричной самой себе.
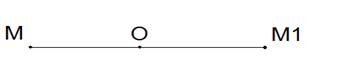 т. М и т.М1 симметричны относительно т.О.
т. М и т.М1 симметричны относительно т.О.
т. О – центр симметрии
т.О – середина отрезка ММ1
т.О отображается сама на себя
Опр. ( осевая симметрия)
Точки А и А1 называются симметричными относительно прямой а ( ось симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка прямой а считается симметричной самой себе.
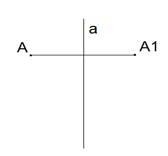
Опр. ( зеркальная симметрия)
Точки АА1 называются симметричными относительно плоскости α( плоскость симметрии), если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости считается симметричной самой себе.
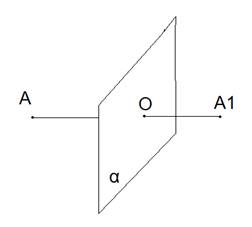
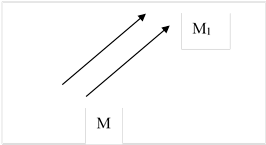
Опр . Параллельным переносом на вектор ![]() называется отображение пространства
на себя, при котором любая точка М переходит в точку М1 , что
называется отображение пространства
на себя, при котором любая точка М переходит в точку М1 , что ![]()
Задачи практической работы:
Практическая работа №14
1 вариант
1. При зеркальной симметрии прямая а отображается на прямую а1 . Докажите, что прямые а и а1 лежат в одной плоскости ( прямые а и а1 параллельны ).
2. При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β1 . Докажите, что если β ║ α , то β1║ α.
3. Докажите, что при параллельном переносе на вектор р, где р ≠ 0 , прямая , не параллельная вектору р и не содержащая этот вектор, отображается на параллельную ей прямую.
2 вариант
1. При зеркальной симметрии прямая а отображается на прямую а1 . Докажите, что прямые а и а1 лежат в одной плоскости ( прямые а и а1 пересекаются ).
2. При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β1 . Докажите, что если β перпендикулярна α , то β1 совпадает с β.
3. Докажите, что при параллельном переносе на вектор р, где р ≠ 0 , прямая , параллельная вектору р или содержащая этот вектор, отображается на себя.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 3. |
Геометрия. Прямые и плоскости в пространстве. Координаты и векторы |
|
|
Тема 3.1 |
Прямые и плоскости в пространстве |
|
Практическое занятие №15. Изображение пространственных фигур
Учебная цель: развитие пространственного воображения студентов при решении геометрических задач, развитие геометрического мышления.
Учебные задачи:
1. Знать методы построения фигур в пространстве.
2. Уметь изображать пространственные фигуры.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
При изображении пространственных фигур необходимо соблюдать следующие требования.
1. Изображение должно быть наглядным. Призму надо изображать так, чтобы наибольшее число её граней были видимыми, чтобы не сливались рёбра.
2. Изображение должно быть простым, т.е. не должно содержать каких-либо построений, не имеющих прямого отношения к решению задачи. Видимые линии должны иметь наибольшую толщину, невидимые – изображать штриховыми линиями.
3. Выполнение чертежа призмы удобно начинать с верхнего основания, т.к. в верхнем основании все линии видимые, боковые рёбра изображаются в виде параллельных и равных отрезков.
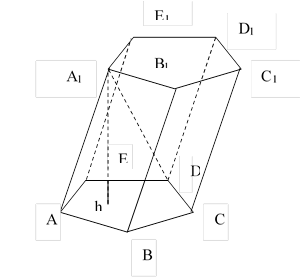
ABCDE A1 B1 C1 D1 – наклонная призма.
ABCDE и A1 B1 C1 D1 E1 - основания призмы
АВВ1 А1 … - боковые грани (параллелограммы)
АА1 , ВВ1 , … - боковые рёбра
h - высота призмы
А1 D – диагональ призмы


Если боковые рёбра призмы перпендикулярны к основаниям, то призма является прямой. Высота прямой призмы равна её боковому ребру.
Прямая призма называется правильной, если её основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.
Задачи практической работы:
Практическая работа № 15
1 вариант.
1) Сторона основания правильной четырёхугольной призмы равна а, а диагональ призмы образует с плоскостью основания угол 45º. Найти:
а) диагональ призмы;
б) площадь сечения призмы плоскостью, проходящей через сторону нижнего основания и противоположную сторону верхнего основания.
2) Основанием прямой призмы является прямоугольный треугольник, гипотенуза которого равна т, а острый угол равен 60º. Через катет, противолежащий этому углу, и противоположную этому катету вершину другого основания проведено сечение, составляющее 45º с плоскостью основания. Доказать, что ∆А1СД прямоугольный. Вычислить площадь основания призмы, высоту призмы.
2 вариант.
1) 2) Диагональ правильной четырёхугольной призмы равна а и образует с плоскостью основания угол
в 30º. Найти: а) сторону основания призмы, б) площадь сечения призмы плоскостью, проходящей через диагонали основания призмы.
2) Сторона основания правильной треугольной призмы равна а, высота призмы равна 1,5 а. Через сторону основания и противоположную вершину другого основания проведено сечение. Найти:
а) высоту основания призмы;
б) угол между плоскостями основания и сечения призмы.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 3. |
Геометрия. Прямые и плоскости в пространстве. Координаты и векторы |
|
|
Тема 3.2 |
Координаты и векторы |
|
Практическое занятие №16. Линейные операции над векторами (правила треугольника, параллелограмма, многоугольника)
Учебная цель: развитие пространственного воображения студентов при решении геометрических задач, применение знаний при выполнении операций над векторами.
Учебные задачи:
1. Знать правила операций над векторами.
2. Уметь выполнять действия с векторами.
Краткие теоретические и учебно-методические материалы
по теме практической работы
Основные определения, обозначения векторов, действия над векторами в пространстве аналогичны основным характеристикам вектора в пространстве.
Действия над векторами
1) Сложение векторов.
Правило треугольника Правило параллелограмма
![]()
![]()
![]()
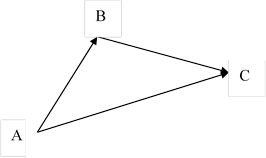
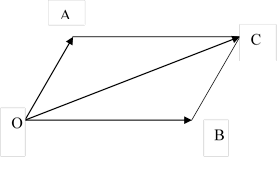
2) Вычитание векторов
![]()
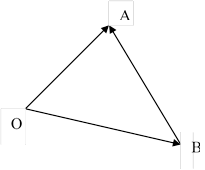
3) Умножение вектора на число:
Опр.
Произведением ненулевого
вектора а на число k называется такой вектор ![]() ,
длина которого равна
,
длина которого равна ![]() , причём векторы
, причём векторы ![]() и
и ![]() сонаправлены
при k > 0 и противоположно направлены при k
< 0
сонаправлены
при k > 0 и противоположно направлены при k
< 0


Для сложении некомпланарных векторов применяют правило параллелепипеда
![]()
![]()
![]()
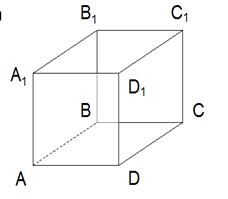
![]()
Задачи практической работы:
Практическая работа № 16
1 вариант
→ →
1) Нарисуйте параллелепипед АВСДА1В1С1Д1 , обозначьте вектор СД и ВС соответственно через
векторы ![]() и
и ![]() .
.
а) Изобразите на рисунке векторы ![]() ,
, ![]() ,
,
![]() ,
, ![]()
б) Изобразите
вектор, начало и конец которого являются вершинами параллелепипеда, равный
сумме векторов ![]()
в)
Разложите вектор ![]() по векторам
по векторам ![]()
2 вариант
→ →
1) Нарисуйте параллелепипед АВСДА1В1С1Д1 , обозначьте вектор СД и АД соответственно через
векторы ![]() и
и ![]() .
.
а) Изобразите на рисунке векторы ![]()
![]() ,
,
![]() ,
, ![]() ,
,
![]()
б) Изобразите
вектор, начало и конец которого являются вершинами параллелепипеда, равный
сумме векторов ![]()
в)
Разложите вектор ![]() по векторам
по векторам ![]()
|
Раздел 3. |
Геометрия. Прямые и плоскости в пространстве. Координаты и векторы |
|
|
Тема 3.2 |
Координаты и векторы |
|
Практическое занятие №17. Действия с векторами, заданными своими координатами
Учебная цель: развитие пространственного воображения студентов при решении геометрических задач, применение знаний при выполнении операций над векторами.
Учебные задачи:
1. Знать правила операций над векторами.
2. Уметь выполнять действия с векторами, заданными координатами.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
При решении задач в координатах применяют правила:
1.
Если вектор ![]() имеет координаты
имеет координаты ![]() , то его можно разложить по
координатным векторам
, то его можно разложить по
координатным векторам
![]() где
где ![]() - координатные векторы.
- координатные векторы.
Пусть даны векторы ![]() и
и
![]()
2.
Если ![]() , то
, то ![]()
3. ![]()
![]()
4. ![]()
5. ![]()
Скалярное произведение векторов:![]()
Скалярное произведение векторов в координатах: ![]()
Вычисление координат середины отрезка
![]()
![]() и
и ![]() - середина отрезка
- середина отрезка
![]()
Вычисление длины вектора по его координатам
![]()
Расстояние между двумя точками
![]()
![]()
Угол между векторами ![]() и
и ![]()
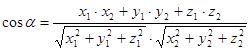
Угол между прямыми , где ![]() и
и ![]() -
направляющие векторы прямых
-
направляющие векторы прямых
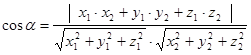
Задачи практической работы:
Практическая работа № 17
1 вариант
1)Даны векторы а{-1; 2; 0 } ,b{0; -5; -2 }, c{2; 1: -3}. Найдите координаты вектора р = 3 в – 2а + с
2) Даны точки А(4; -3; 5), В(6; -7; 5), С(5; 2; 1) и Д(3; 6; 1). Докажите, что АВСД – параллелограмм.
3) Вычислите угол между векторами АВ и СD , если А(3; -2; 4), В(4; -1; 2), С(6; -3; 2) , D(7; -3; 1)
4) Даны векторы а = 5 i - 2 j + 4 k и в = 3 j + 2 k . Вычислите а · в.
5) Найти координаты центра и радиус сферы, заданной
уравнением ( х – 2 )2 + ( у + 3 )2 = 25.![]()
![]()
2 вариант
1) Даны векторы а{-1; 2; 0 } ,b{0; -5; -2 }, c{2; 1: -3}. Найдите координаты вектора п =3 с – 2в + а
2) Даны точки А(3; 5; 4), В(4; 6; 5), С(6; -2; 1) и Д(5; -3; 0). Докажите, что АВСД – параллелограмм.
3) Определите угол А треугольника, вершинами которого являются точки А(1; -1; 3), В(3; -1; 1), С(-1; 1; 3)
4) Даны векторы а = 5 i - 2 j + 4 k и в = 3 j + 2 k . Вычислите а · в.
5) Написать уравнение сферы радиуса R с центром в точке А, если А( 2; 0; -1 ) , R = 7.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 4 |
Основы тригонометрии |
|
|
Тема 4.1 |
Основы тригонометрии. Решение тригонометрических уравнений и неравенств |
|
Практическое занятие №18. Вычисление тригонометрических функций.
Учебная цель: Вычисление значений тригонометрических функций некоторых углов, заданных в радианах (градусах).
Учебные задачи:
1. Формирование умений и навыков применения единичной окружности для вычисления значений синуса, косинуса, тангенса углов.
2. Уметь решать задачи с использованием формул тригонометрии.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Таблица
значений ![]() ,
, ![]() ,
,
![]() ,
, ![]()
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
1/2 |
|
|
1 |
0 |
– 1 |
0 |
|
|
1 |
|
|
1/2 |
0 |
– 1 |
0 |
1 |
|
|
0 |
|
1 |
|
не сущ. |
0 |
не сущ. |
0 |
|
|
не сущ. |
|
1 |
|
0 |
не сущ. |
0 |
не сущ. |
Знаки синуса, косинуса, тангенса и котангенса по четвертям
![]()
![]()
![]()
![]() у
у
![]() у
у
![]() ,
, ![]() у
у
х х х
Основные формулы тригонометрии
1. Зависимость между синусом, косинусом, тангенсом и котангенсом одного и того же аргумента:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
2. Формулы кратных углов:
![]() ,
, ![]() =
=![]() ,
,
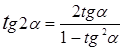 ,
, ![]() ,
, ![]() .
.
3. Формулы сложения:
![]() ,
,
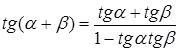 ,
,
![]() ,
,
![]() ,
,
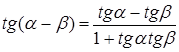 .
.
![]() ,
,
4. Формулы преобразования сумм или разностей в произведения:
![]() ,
,
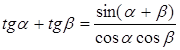 ,
,
![]() ,
,
![]() ,
,
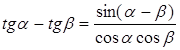 .
.
![]() ,
,
5. Формулы понижения степени (формулы половинного аргумента):
![]() ,
, ![]()
![]() ,
, ![]() .
.
6. Формулы преобразования произведений в суммы или разности:
![]() ,
,![]() ,
,
![]() .
.
7.
Синус, косинус, тангенс и котангенс углов ![]() и
и
![]() :
:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
8.
Периодичность синуса, косинуса, тангенса и котангенса ![]() :
: ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Задачи практической работы:
Практическая работа № 18
Вариант № 1
1. Вычислить: а) ![]() ;
б)
;
б) ![]() .
.
2. Вычислить:
![]()
3. Упростить выражение:
а) ![]() б)
б) ![]()
Вариант № 2
1. Вычислить: а) ![]() ;
б)
;
б) ![]() .
.
2. Вычислить:
![]()
3. Упростить выражение:
а) ![]() б)
б) ![]()
Вариант № 3
1. Вычислить: а) ![]() ;
б)
;
б) ![]() .
.
2. Вычислить: ![]()
3. Упростить выражение:
а) ![]() б)
б) ![]()
Вариант № 4
1. Вычислить: а) ![]() ;
б)
;
б) ![]() .
.
2. Вычислить:
![]()
3. Упростить выражение:
а) ![]() б)
б) ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 4 |
Основы тригонометрии |
|
|
Тема 4.1 |
Основы тригонометрии. Решение тригонометрических уравнений и неравенств |
|
Практическое занятие №19. Тождественные преобразования тригонометрических функций Вычисление тригонометрических функций.
Учебная цель: использование тригонометрических формул для преобразования тригонометрических выражений.
Учебные задачи:
1. Формирование умений и навыков применения тригонометрических формул для преобразования тригонометрических выражений.
2. Уметь решать задачи с использованием формул тригонометрии.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
При доказательстве тригонометрических тождеств обычно используют следующие способы:
1. Выражение, стоящее в одной части равенства, с помощью тождественных преобразований приводят к выражению, стоящему в другой части равенства.
2. Выражения, стоящие в левой и правой части тождества с помощью тождественных преобразований приводят к одному и тому же виду.
3. Доказывают, что разность между левой и правой частью тождества равны нулю.
При доказательстве тригонометрических тождеств используют основные соотношения между тригонометрическими функциями одного и того же аргумента, формулы приведения, формулы сложения, формулы для двойного и половинного аргумента, формулы преобразования суммы тригонометрических функций в произведение, а также числовые значения тригонометрических функций для некоторых углов.
Пример
1 Доказать тождество: ![]()
Доказательство:
![]() - правая часть
- правая часть
![]()
Пример
2 Доказать тождество: ![]()
Доказательство:
![]()
Задачи практической работы:
Практическая работа № 19
1 вариант
Задание 1. Доказать тождество: ![]()
Задание 2. Упростить выражение: а) ![]() ; б)
; б) ![]()
Задание 3. Вычислить ![]() ,
если
,
если ![]() ;
; ![]() ,
,
![]() ,
, ![]()
Задание 4. Используя формулы приведения , вычислить:
1) cos 780º ; 2) sin ![]()
Задание 5. Какие значения может принимать ![]() , если
, если ![]()
2 вариант
Задание 1. Доказать тождество: ![]()
Задание 2. Упростить выражение: а) ![]() б)
б) ![]()
Задание 3. Вычислить ![]()
Задание 4. Используя формулы приведения , вычислить:
1) sin 780º ; 2) cos ![]()
Задание 5. Какие значения может принимать ![]()
3 вариант
Задание 1. Доказать тождество: ![]()
Задание 2. Упростить выражение: а)  б)
б) ![]()
Задание 3. Вычислить ![]() ,
если cos z
= - 0,8
,
если cos z
= - 0,8 ![]()
Задание 4. Используя формулы приведения , вычислить:
1) sin 750º ; 2) cos ![]()
Задание 5. Какие значения может принимать ![]()
4 вариант
Задание 1. Доказать тождество: ![]()
Задание 2. Упростить выражение.
a)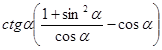 б)
б) ![]()
Задание 3. Вычислить ![]()
Задание 4. Используя формулы приведения , вычислить:
1) cos 750º ; 2) sin ![]()
Задание 5. Какие значения может принимать ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 4 |
Основы тригонометрии |
|
|
Тема 4.1 |
Основы тригонометрии. Решение тригонометрических уравнений и неравенств |
|
Практическое занятие №20. Решение тригонометрических уравнения общего вида.
Учебная цель: применение различных методов решения тригонометрических уравнений.
Учебные задачи:
1. Научиться определять тип тригонометрического уравнения.
2. Научиться решать тригонометрические уравнения различными методами
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Уравнения вида sin x = a , cos x = a , tg x = a называются простейшими. Для них выведены формулы корней:
![]() sin x = a
sin x = a ![]()
![]()
![]()
![]()
![]()
![]()
![]()
К этим уравнениям сводятся все другие. Для большинства таких уравнений требуется применение различных формул и преобразование тригонометрических выражений.
1. Уравнения, сводящиеся к квадратным ![]() . Вводят новую переменную sin x=
t
. Вводят новую переменную sin x=
t

2. Уравнения вида ![]() а
≠ 0, b ≠ 0 называются однородными
относительно sin x и cos x. Оно решается делением обеих частей на cos x ≠ 0 . В результате получается уравнение
а
≠ 0, b ≠ 0 называются однородными
относительно sin x и cos x. Оно решается делением обеих частей на cos x ≠ 0 . В результате получается уравнение
![]() . Этим же способом
решается уравнение 2 sin2 x
– 5 sin x
· cos x
+ 3 cos 2 x = 0 . Обе части уравнения делятся на cos 2 x или
sin 2 x .
. Этим же способом
решается уравнение 2 sin2 x
– 5 sin x
· cos x
+ 3 cos 2 x = 0 . Обе части уравнения делятся на cos 2 x или
sin 2 x .


3. Уравнения, решаемые разложением левой части на множители
Пример
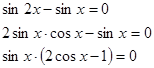 Общий
множитель sin x выносится за скобки.
Общий
множитель sin x выносится за скобки.
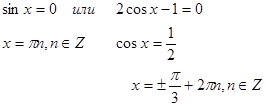
Ответ: ![]()

Если уравнение имеет две серии
корней, полученных при решении тригонометрических уравнений, имеющую общую
часть, в ответе можно оставлять обе серии. Например, х = πn; x = ![]()
Задачи практической работы:
Практическая работа № 20
Вариант № 1
1. Решить уравнение:
1) ![]() ;
;
2) ![]()
2. Найти корни уравнения ![]() на
отрезке
на
отрезке ![]()
3. Решить уравнение:
1) ![]()
2) ![]()
4. Найдите наибольший
отрицательный корень уравнения: ![]()
Вариант № 2
1. Решить уравнение:
1) ![]() ;
;
2) ![]()
2. Найти корни уравнения ![]() на
отрезке
на
отрезке ![]()
3. Решить уравнение:
1) ![]()
2) ![]()
4. Найдите наибольший
отрицательный корень уравнения: ![]()
Вариант № 3
1. Решить уравнение:
1) ![]() ;
;
![]()
2. Найти корни уравнения ![]() на
отрезке
на
отрезке ![]()
3. Решить уравнение:
![]()
2) ![]()
4. Найдите наибольший
отрицательный корень уравнения: ![]()
Вариант № 4
1. Решить уравнение:
1) ![]() ;
;
![]()
2. Найти корни уравнения ![]() на
отрезке
на
отрезке ![]()
3. Решить уравнение:
![]()
![]()
4. Найдите наибольший
отрицательный корень уравнения: ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 4 |
Основы тригонометрии |
|
|
Тема 4.1 |
Основы тригонометрии. Решение тригонометрических уравнений и неравенств |
|
Практическое занятие №21. Решение тригонометрических неравенств.
Учебная цель: применение различных методов решения тригонометрических неравенств.
Учебные задачи:
1. Научиться определять тип тригонометрического неравенства.
2. Научиться решать тригонометрические неравенства различными методами
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр.
Неравенства, содержащие переменную под знаком тригонометрической функции, называются тригонометрическими.
При решении тригонометрических неравенств используют единичную окружность.
Задача Решить неравенство cos x > ![]()
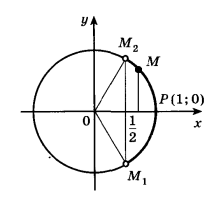
По определению cos x – это абсцисса точки единичной окружности. Абсциссу, равную
![]() , имеют две точки единичной
окружности М1 и М2 . Абсциссу, большую
, имеют две точки единичной
окружности М1 и М2 . Абсциссу, большую ![]() имеют все точки М дуги единичной
окружности, лежащие правее прямой М1М2 . Таким образом,
решениями неравенства cos x >
имеют все точки М дуги единичной
окружности, лежащие правее прямой М1М2 . Таким образом,
решениями неравенства cos x > ![]() являются все
числа х из промежутка
являются все
числа х из промежутка ![]() .
.
Все решения данного неравенства – множество интервалов ![]()
![]()
Ответ: ![]()
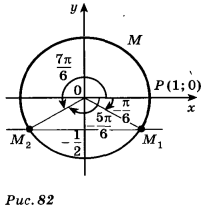

Задачи практической работы:
Практическая работа № 21
1 вариант.
Решить неравенства:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() 5)
5)
![]()
2 вариант.
Решить неравенства:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() 5)
5) ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 5 |
Начала математического анализа |
|
|
Тема 5.1 |
Последовательности. Производная |
|
Практическое занятие №22. Вычисление предела числовой последовательности
Учебная цель: Рассмотреть виды последовательностей. Способы заданий последовательностей.
Учебные задачи:
1. Научиться определять вид последовательности.
2. Научиться задавать последовательности.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Бесконечной числовой последовательностью называется числовая функция, определенная на множество N натуральных чисел.
Последовательность
![]() называется возрастающей (убывающей),
если каждый член, начиная со второго, не больше (не меньше) предыдущего, то
есть если для любого n выполняется неравенство
называется возрастающей (убывающей),
если каждый член, начиная со второго, не больше (не меньше) предыдущего, то
есть если для любого n выполняется неравенство ![]() .
.
Последовательность
![]() называется невозрастающей (неубывающей),
если каждый ее член, начиная со второго, не больше (не меньше) предыдущего, то
есть если для любого n выполняется
неравенство
называется невозрастающей (неубывающей),
если каждый ее член, начиная со второго, не больше (не меньше) предыдущего, то
есть если для любого n выполняется
неравенство ![]() .
.
Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными.
Последовательность
![]() называется ограниченной сверху
(ограниченной снизу), если можно указать такое число М (число m), что для всех членов этой последовательности
выполняется неравенство
называется ограниченной сверху
(ограниченной снизу), если можно указать такое число М (число m), что для всех членов этой последовательности
выполняется неравенство ![]() .
Числа M и m называются соответственно верхней и нижней
границами последовательности
.
Числа M и m называются соответственно верхней и нижней
границами последовательности ![]() .
Тот факт, что последовательность ограничена сверху числом М (снизу
числом m), геометрически означает, что ни одна
точка
.
Тот факт, что последовательность ограничена сверху числом М (снизу
числом m), геометрически означает, что ни одна
точка ![]() не лежит правее
точки М (левее точки m).
не лежит правее
точки М (левее точки m).
Последовательность
![]() называется ограниченной,
если существуют два числа m и М такие,
что для всех n выполняется неравенство
называется ограниченной,
если существуют два числа m и М такие,
что для всех n выполняется неравенство ![]() . Тот факт, что последовательность
ограничена числами m и
M, геометрически означает, что все ее
члены помещаются в промежутке [m, M].
. Тот факт, что последовательность
ограничена числами m и
M, геометрически означает, что все ее
члены помещаются в промежутке [m, M].
Последовательность
![]() называется постоянной,
если все ее члены совпадают.
называется постоянной,
если все ее члены совпадают.
Обычно последовательность задается формулой, выражающей общий член последовательности через n. Иногда указывается правило, с помощью которого можно вычислить n-й член последовательности по ее известным предыдущим членам. Такой способ задания последовательности называется индуктивным (или рекуррентным).
Пример
. Вычислить пять первых членов последовательности ![]()
Решение. Подставив вместо n
последовательно 1, 2, 3, 4, 5, получим ![]() ,
,
![]()
Задачи практической работы:
Практическая работа № 22
Вариант 1
Вычислите пять первых членов последовательностей:
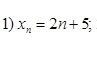
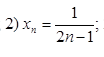
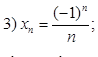
Вариант 2
Вычислите пять первых членов последовательностей:
![]()
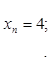
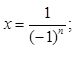
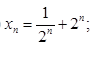
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 5 |
Начала математического анализа |
|
|
Тема 5.1 |
Последовательности. Производная |
|
Практическое занятие №23. Техника дифференцирования функций
Практическое занятие №24. Составление уравнения касательной к графику функции
Учебная цель: вычисление производных функций по определению и таблице производных.
Учебные задачи:
1. Научиться дифференцировать функции.
2. Научиться находить значение производной в точке.
3. Научиться составлять уравнение касательной к графику функции
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр.
Производной функции f(x) в точке х называется предел разностного отношения ![]() при
при ![]() .
.
![]() .
.
Опр.
Операция нахождение производной называется дифференцированием.
Это правило является основным, т.к. выведено из самого определения. Однако при дифференцировании сложных функций, суммы, произведения, частного применение общего правила представляет большие трудности. Поэтому применяют правила дифференцирования.
Правила
1. ![]() -
Производная суммы равна сумме производных.
-
Производная суммы равна сумме производных.
2. ![]() -
Постоянный множитель можно вынести за знак производной.
-
Постоянный множитель можно вынести за знак производной.
3. ![]() - Производная
произведения.
- Производная
произведения.
4. 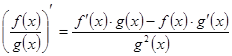 Производная
частного
Производная
частного
Формулы дифференцирования
1.
С′ =
0 11. ![]()
2.
( х ) ′ =
1 12. ![]()
3.
( х 2 ) ′ =
2х 13. ![]()
4. ( х 3) ′ = 3х2
5.
( х р ) ′ = р х р – 1
14. ![]()
6.
( е х ) ′ = е х![]() 15.
15. ![]()
7. ![]() 16.
16. ![]()
8. 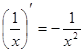 17.
17.
![]()
9. ![]() 18.
18.
![]()
10. ![]()
Примеры:
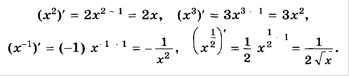

При решении задач на нахождение уравнения касательной к
графику функции в точке используется геометрический смысл производной ![]()
Уравнение касательной ![]()
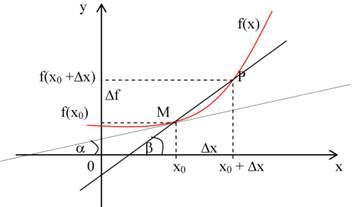
Общая схема составления уравнения касательной к графику функции y = f(x):
1. Определить х0.
2. Вычислить f(x0).
3. Вычислить f’(x)
4. Вычислить f’(x0)
5. Подставить полученные значения в уравнение касательной y= f(x0) + f’(x0)*(x - x0).
Задача. Найти уравнение касательной к графику функции f(x) = x3 – 2*x2 + 1 в точке х = 2.
1. х0 = 2.
2. f(x0) = f(2) = 22 - 2*22 + 1 = 1.
3. f’(x) = 3*x2 – 4*x.
4. f’(x0) = f’(2) = 3*22 – 4*2 = 4.
5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x - 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x - 7.
Ответ: y = 4*x - 7.
Задачи практической работы:
Практические работы № 23-24
1 вариант
Задание 1. Найти производную функции.
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д)
![]() е)
е) ![]()
Задание 2. Решить
уравнение f′(x) = 0,
если ![]()
Задание 3. Написать уравнение касательной к графику функции у = f(x) в точке с абсциссой х0
![]() х0 = 2
х0 = 2
2 вариант
Задание 1. Найти производную функции.
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д)
![]() е)
е) ![]()
Задание 2. Решить
уравнение f′(x) = 0,
если ![]()
Задание 3. Написать уравнение касательной к графику функции у = f(x) в точке с абсциссой х0
![]() х0 = 3.
х0 = 3.
3 вариант
Задание 1. Найти производную функции.
а) ![]() б)
б)
![]() в)
в) ![]()
г) ![]() д)
д)
![]() е)
е) ![]()
Задание 2. Решить
уравнение f′(x) = 0,
если ![]()
Задание 3. Найти угол между осью Ох и касательной к графику функции у=f(x) в точке с абсциссой х0 и написать уравнение касательной в этой точке.
![]()
![]()
4 вариант
Задание 1. Найти производную функции.
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д)
![]() е)
е) ![]()
Задание 2. Решить
уравнение f′(x) = 0,
если ![]()
Задание 3. Найти угол между осью Ох и касательной к графику функции у=f(x) в точке с абсциссой х0 и написать уравнение касательной в этой точке.
![]()
![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 5 |
Начала математического анализа |
|
|
Тема 5.1 |
Последовательности. Производная |
|
Практическое занятие №25. Исследование функции и построение её графика с помощью производной
Учебная цель: Исследование функции с помощью производной и построение её графика.
Учебные задачи:
1. Научиться проводить исследование функции.
2. Научиться строить график функции по результатам исследования.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Общее исследование функции и построение её графика рекомендуется выполнять по следующей схеме:
1. Найти область определения функции
2. Производную
3. Стационарные точки
4. Производную
5. Промежутки возрастания и убывания
6. Точки экстремума и значение функции в этих точках.
Задача
Построить график функции ![]()
Решение
2. Производная : ![]()
1. Область определения: ![]()
3. Стационарные точки: ![]()
![]()
![]()
![]()
5. Промежутки возрастания и убывания
![]()
![]()
6. Точки экстремума и значение функции в этих точках.
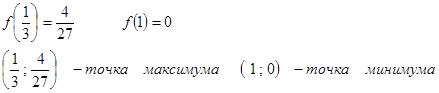
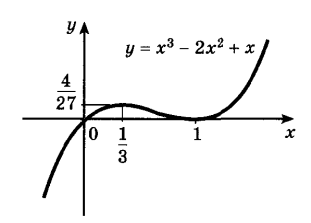
Задачи практической работы:
Практическая работа № 25
Вариант 1.
Задание 1.
Исследовать функцию с помощью производной и построить её график.
а) ![]() б)
б) ![]()
Вариант 2.
Задание 1.
Исследовать функцию с помощью производной и построить её график.
а) ![]() б)
б) ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 5 |
Начала математического анализа |
|
|
Тема 5.2 |
Первообразная и интеграл |
|
Практическое занятие №26. Решение задач на связь первообразной и её производной
Учебная цель: применение производной к решению задач.
Учебные задачи:
1. Знать таблицу первообразных.
2. Научиться находить первообразную различных функций.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Основные понятия и определения
Функция ![]() называется первообразной функцией для функции
называется первообразной функцией для функции ![]() на промежутке (a; b),
если для всех xÎ(a;
b) выполняется равенство:
на промежутке (a; b),
если для всех xÎ(a;
b) выполняется равенство:
![]() .
(1)
.
(1)
Например,
для ![]() первообразная
первообразная
![]() , так как
, так как  ;
;
для ![]() первообразная
первообразная
![]() , так как
, так как ![]() ;
;
для ![]() первообразная
первообразная
![]() , так как
, так как ![]() .
.
Множество всех первообразных для функции f(x) на промежутке (a;b) называется неопределенным интегралом и обозначается
![]() ,
(2)
,
(2)
где ![]() - первообразная функции
- первообразная функции ![]() на промежутке (a; b);
на промежутке (a; b);
знак ![]() называется интегралом.
называется интегралом.
Приняты следующие термины:
![]() - подынтегральная функция;
- подынтегральная функция;
![]() - подынтегральное
выражение;
- подынтегральное
выражение;
![]() - переменная
интегрирования;
- переменная
интегрирования;
![]() - постоянная
интегрирования.
- постоянная
интегрирования.
Наличие в этой
формуле произвольной постоянной величины ![]() объясняет, почему интеграл
объясняет, почему интеграл ![]() называется неопределенным.
называется неопределенным.
Операция нахождения неопределенного интеграла от заданной функции называется интегрированием.
Интегрирование представляет собой операцию, обратную дифференцированию.
Для проверки, правильно ли найден интеграл, полученный результат дифференцируют (должны получить подынтегральную функцию).
Пример: 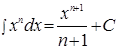 , так как
, так как  .
.
Пример. Найти первообразную и сделать проверку:
1. I=![]() .
.
Решение. Разбиваем интеграл на три интеграла и работаем с каждым:
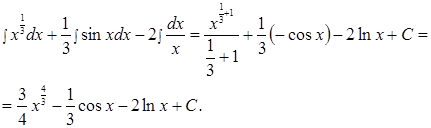
Дифференцированием первообразной проверим правильность интегрирования:
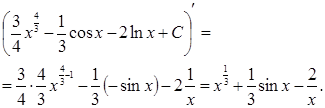
Полученное выражение совпадает с подынтегральной функцией, т.е. интегрирование проведено правильно.
Ответ. ![]()
Задачи практической работы:
Практическая работа № 26
Вариант 1
Найти первообразную и сделать проверку:
![]()
![]()
![]()
Вариант 2
Найти первообразную и сделать проверку:
![]()
![]()
![]()
Вариант 3
Найти первообразную и сделать проверку:
![]()
![]()
![]()
Вариант 4
Найти первообразную и сделать проверку:
![]()
![]()
![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 5 |
Начала математического анализа |
|
|
Тема 5.2 |
Первообразная и интеграл |
|
Практическое занятие №27. Вычисление неопределённого и определённого интегралов
Учебная цель: применение знаний для вычисления интегралов.
Учебные задачи:
1. Научиться вычислять неопределенный интеграл.
2. Научиться вычислять определенный интеграл.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Таблица неопределенных интегралов
|
1. |
9. |
|
2. |
10. |
|
3. |
11. |
|
4. |
12. |
|
5. |
13. |
|
6. |
14. |
|
7. |
15. |
|
8. |
|
Свойства неопределенного интеграла
|
1. |
4. |
|
2. |
5. |
|
3. |
6. |
|
|
|
Задачи практической работы:
Практическая работа № 27
1 вариант
Вычислить определённый интеграл с помощью основных свойств и формулы Ньютона-Лейбница
1) ![]() ; 2)
; 2) 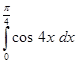 ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) 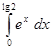 ; 6)
; 6) ![]()
2 вариант
Вычислить определённый интеграл с помощью основных свойств и формулы Ньютона-Лейбница
1) ![]() ; 2)
; 2) 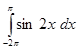 ; 3)
; 3) 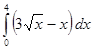 ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) 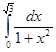
3 вариант
Вычислить определённый интеграл с помощью основных свойств и формулы Ньютона-Лейбница
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) 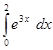 ;
;
4) ![]() ; 5)
; 5) 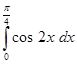 ; 6)
; 6) ![]()
4 вариант
Вычислить определённый интеграл с помощью основных свойств и формулы Ньютона-Лейбница
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) 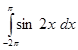 ;
;
4)  ; 5)
; 5) 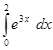 ;
;![]() 6)
6)
![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 5 |
Начала математического анализа |
|
|
Тема 5.2 |
Первообразная и интеграл |
|
Практическое занятие №28. Применение интеграла к вычислению физических величин и площадей плоских фигур
Учебная цель: применение знаний для вычисления площадей плоских фигур.
Учебные задачи:
1. Научиться находить путь материальной точки с помощью определенного интеграла.
2. Научиться вычислять площадь фигуры с помощью определенного интеграла.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Фигура, изображённая на рисунке является криволинейной трапецией
|
|
Определение
Криволинейной трапецией называется фигура, ограниченная сверху графиком непрерывной функции y=f(x), снизу отрезком [a;b] оси Ох, а с боков отрезками прямых х=а, х=b
Площадь криволинейной трапеции можно вычислить с помощью определённого интеграла
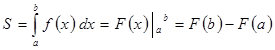
![]() Возможно такое
расположение:
Возможно такое
расположение:
S = S1 + S2
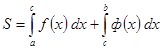
Возможен следующий случай, когда f(x) < 0 на [а,b]
|
|
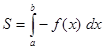
Возможно и такое расположение
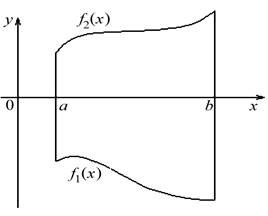 S=
S=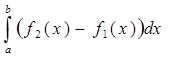
Задачи на вычисление площадей плоских фигур можно решать по следующему плану:
1) по условию задачи делают схематический чертёж;
2) представляют искомую фигуру как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции.
3)
записывают каждую функцию в виде ![]()
4) вычисляют площадь каждой криволинейной трапеции и искомой фигуры.
Задача
Найти площадь фигуры, ограниченной линиями.
![]()
S = ![]() dx =
dx =![]() dx =
dx =
= (-![]() |
|![]() =-
=- ![]() (кв. ед.)
(кв. ед.)
Задачи практической работы:
Практическая работа № 28
1 вариант
Найти площадь фигуры, ограниченной линиями
а) параболой у = (х + 1)2 , прямой у = 1 – х и осью Ох.
б) параболой у = х2 – 4х +3 и осью Ох.
в) графиком функции у = sin x , и отрезком [ π ; 2π] оси Ох.
2 вариант
Найти площадь фигуры, ограниченной линиями
а) параболой у = 4 - х2 и осью Ох.
б) графиком функции у = ![]() ,
прямой у = х + 2 и прямыми х= 0, х = 4.
,
прямой у = х + 2 и прямыми х= 0, х = 4.
в) графиком функции у = cos x ![]() и
отрезком [
и
отрезком [ ![]() ] оси Ох.
] оси Ох.
3 вариант
Найти площадь фигуры, ограниченной линиями
а) параболой у = х2 + 4х - 3 и осью Ох.
б) параболой у = х2 + 1 и прямой у = 3 - х .
в) параболой у = -х2 .
4 вариант
Найти площадь фигуры, ограниченной линиями
а) параболой у = х ( 2 – х ) и осью Ох.
б) параболой у = 6 х - х2 и прямой у = х - 4 .
в) параболой у = 2 - х2 и прямой у = - х .
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 6 |
Геометрия. Многогранники и круглые тела. Измерения в геометрии |
|
|
Тема 6.1 |
Многогранники, их измерения |
|
Практическое занятие №29. Решение задач на вычисление площадей плоских фигур с применением соответствующих формул и фактов из планиметрии
Учебная цель: применение знаний для вычисления площадей плоских фигур.
Учебные задачи:
1. Знать формулы вычисления периметра, площадей и других измерений геометрических фигур.
2. Научиться вычислять площадь фигуры.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
ПЛАНИМЕТРИЯ
![]() A Произвольный
треугольник
A Произвольный
треугольник
c b
![]() - стороны,
- стороны, ![]() - высота, проведенная к стороне а,
- высота, проведенная к стороне а,
ha S – площадь треугольника,
B
а C ![]() радиус вписанной окружности,
радиус вписанной окружности,
![]() радиус
описанной окружности, р – полупериметр
радиус
описанной окружности, р – полупериметр 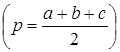 ,
,
![]() ,
, ![]() , где С – угол между
сторонами a и b,
, где С – угол между
сторонами a и b,
![]() ,
, ![]() ,
, ![]() (формула Герона);
(формула Герона);
![]() (теорема косинусов);
(теорема косинусов);
![]() (теорема синусов),
(теорема синусов),
где А, В, С – углы, лежащие против сторон а, b, с соответственно.
Прямоугольный треугольник (![]() катеты, с - гипотенуза)
катеты, с - гипотенуза)
![]()
![]() ;
; ![]() ;
; ![]() ;
;
b
с ![]() (теорема
Пифагора)
(теорема
Пифагора)
a
Параллелограмм
(![]() - смежные стороны,
- смежные стороны, ![]() угол между ними,
угол между ними, ![]() высота, проведенная к а,
высота, проведенная к а, ![]() диагонали,
диагонали,![]() угол между ними)
угол между ними)
![]()
![]() ,
,
b hа
![]() ,
, ![]() .
.
![]()
a
![]() Ромб
Ромб
![]() (а –
сторона ромба,
(а –
сторона ромба, ![]() –острый
угол ромба,
–острый
угол ромба,
![]() высота,
высота, ![]() диагонали)
диагонали)
a ![]() ;
; ![]() ;
; ![]() .
.
Прямоугольник
(![]() диагональ,
диагональ, ![]() - смежные стороны,
- смежные стороны, ![]() угол между)
угол между)
![]()
![]()
b
![]()
![]()
a
Квадрат
(а – сторона квадрата, r – радиус вписанной окружности, R – радиус описанной окружности, d - диагональ)
![]()
a d
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Квадрат обладает всеми свойствами прямоугольника и ромба.
Трапеция
(а, b – основания, h- высота)
![]() b
b ![]()
h
a
Окружность, круг
(С–длина окружности, S – площадь круга, r –радиус)
![]()
![]()
Сектор
![]() ,
, ![]() – угол в
радианах;
– угол в
радианах;
![]() ,
, ![]() , где
, где ![]() содержит n градусов.
содержит n градусов.
Задачи практической работы:
Практическая работа № 29
Вариант 1
1. Найти основание равнобедренного треугольника, если его боковая сторона равна 23, а периметр равен 81.
2.
Найти третью сторону прямоугольного треугольника, если даны две
другие его стороны ![]() и 4.
и 4.
3. Одна из сторон параллелограмма равна 21, а периметр равен 123. Найти длину стороны параллелограмма, смежной с данной.
4. Хорда делит окружность на части в отношении 5:7. Найти вписанный угол, опирающийся на меньшую из дуг, стягиваемых этой хордой.
Вариант 2
1.
Найти площадь прямоугольного треугольника с катетом 2,5 и гипотенузой ![]() .
.
2. Гипотенуза
равнобедренного прямоугольного треугольника равна 2(![]() . Найти его периметр.
. Найти его периметр.
3.
Одна из диагоналей параллелограмма, равная ![]() , составляет с основанием
, составляет с основанием ![]()
![]() . Найти длину второй диагонали,
если она составляет с тем же основанием угол
. Найти длину второй диагонали,
если она составляет с тем же основанием угол ![]() .
.
4.
Окружность радиуса 6![]() описана
около равнобедренного треугольника с углом
описана
около равнобедренного треугольника с углом ![]() . Найти его основание.
. Найти его основание.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 6 |
Геометрия. Многогранники и круглые тела. Измерения в геометрии |
|
|
Тема 6.1 |
Многогранники, их измерения |
|
Практическое занятие №30. Построение сечений, разверток многогранников. Нахождение основных элементов многогранников
Учебная цель: применение знаний для построения сечений многогранников.
Учебные задачи:
1. Знать методы сечений.
2. Уметь строить развертку фигуры.
3. Знать формулы для нахождения основных элементов многогранников.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Для решения задач на построение сечений многогранника, надо знать основные понятия.
Опр.
Секущей плоскостью называется любая плоскость, по обе стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает грани многогранника по отрезкам.
Опр.
Многогранник, сторонами
которого являются эти отрезки, называется сечением многогранника.. Так как тетраэдр
имеет 4 грани, то его сечениями могут
быть только треугольники и 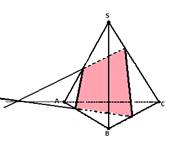
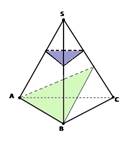
Параллелепипед имеет 6 граней. Его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.
При построении сечений параллелепипеда следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны.
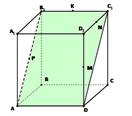
Задача
Точка М лежит на боковой грани АDВ. Построить сечение тетраэдра плоскостью, проходящей через точку М и параллельно основанию АВС.
Решение
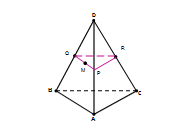
α - секущая плоскость.
![]()
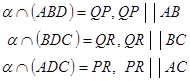
Отсюда вытекает следующий способ построения искомого сечения.
Проведём через точку М прямую, параллельную отрезку АВ, и обозначим буквами P и Q точки пересечения этой прямой с боковыми рёбрами DA и DB. Затем через точку Р проведём прямую, параллельную отрезку АС, и обозначим буквой R точку пересечения этой прямой с ребром DC. Треугольник PQR – искомое сечение.
Задачи практической работы:
Практическая работа № 30
1 вариант.
1) Дан тетраэдр DABC. Точка М – середина ребра AD. Построить сечение тетраэдра плоскостью, проходящей через т.М и параллельно грани АВС. Найти периметр сечения, если ребро тетраэдра равно а.
2) Изобразите параллелепипед АВСDА1В1С1D1 и постройте его сечение плоскостью АВС1 . Докажите, что построенное сечение является параллелограммом.
3) Дан куб АВСDА1В1С1D1 . Постройте сечение плоскостью АСD1 и найдите периметр сечения, если ребро куба равно а.
2 вариант.
1) Дан тетраэдр DABC. Точка М – середина ребра AВ. Построить сечение тетраэдра плоскостью, проходящей через т.М и параллельно грани DВС. Найти периметр сечения, если ребро тетраэдра равно а.
2) Изобразите параллелепипед АВСDА1В1С1D1 и постройте его сечение плоскостью АСС1 . Докажите, что построенное сечение является параллелограммом.
3) Дан куб АВСDА1В1С1D1 . Точка К – середина ребра В1С1 Постройте сечение плоскостью, проходящей через точки А, В, К и найдите периметр сечения, если ребро куба равно а.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 6 |
Геометрия. Многогранники и круглые тела. Измерения в геометрии |
|
|
Тема 6.1 |
Многогранники, их измерения |
|
Практическое занятие №31. Вычисление площадей поверхностей и объемов многогранников.
Учебная цель: применение знаний для вычисления площадей и объемов многогранников.
Учебные задачи:
1. Знать формулы площадей и объемов фигур.
2. Уметь строить многогранники.
3. Уметь вычислять объемы фигур.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
1. Объём
куба вычисляется по формуле: ![]() ,
где а – ребро куба.
,
где а – ребро куба.
![]()
2. Объём
прямоугольного параллелепипеда вычисляется по формуле: ![]() ,
,
где а, в, с – измерения прямоугольного параллелепипеда ( длина, ширина, высота)
![]()
![]()
3. Объём
призмы равен ![]()
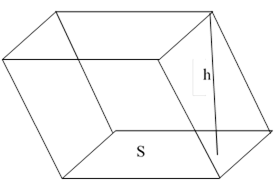
4. Объём
цилиндра вычисляется по формуле: ![]()
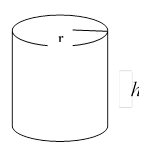
Задачи практической работы:
Практическая работа № 31
1 вариант.
1. Диагональ правильной четырёхугольной призмы равна 4 см и составляет с плоскостью боковой грани угол 30º . Найдите объём призмы.
2. Основанием прямой призмы является ромб со стороной 12 см и острым углом в 60º. Меньшее из диагональных сечений является квадратом. Найти объём призмы.
3. В куб вписан шар. Найдите отношение объёмов куба и шара.
4. Основание прямой призмы – прямоугольный треугольник с гипотенузой 10 см и катетом 6 см. Больший катет треугольника в основании призмы равен диагонали меньшей из боковых граней. Найти объём призмы.
2 вариант.
1. Найти объём прямоугольного параллелепипеда, у которого стороны основания равны 12 см и 16 см, а диагональ параллелепипеда составляет 45º с плоскостью основания.
2. Основанием прямой призмы является ромб со стороной 6 см и острым углом в 60º. Меньшее из диагональных сечений является квадратом. Найти объём призмы.
3. Диаметр шара равен высоте цилиндра, осевое сечение которого – квадрат. Найти отношение объёмов шара и цилиндра.
4. Основание прямой призмы – прямоугольный треугольник с гипотенузой 10 см и катетом 6 см. Больший катет треугольника в основании призмы равен диагонали меньшей из боковых граней. Найти объём призмы.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 6 |
Геометрия. Многогранники и круглые тела. Измерения в геометрии |
|
|
Тема 6.2 |
Тела и поверхности вращения, их измерения |
|
Практическое занятие №32. Изображение тел вращения, их развертки, сечений. Нахождение основных элементов цилиндра, конуса, шара.
Учебная цель: применение знаний для построения тел вращения и нахождения их основных элементов.
Учебные задачи:
1. Знать тела вращения.
2. Уметь строить тела вращения, развертки, сечения.
3. Уметь находить основные элементы цилиндра, конуса, шара.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Для решения задач важно правильно построить изображение фигур.
1. При построении цилиндра:
Изображение цилиндра лучше начинать с построения осевого сечения цилиндра, в котором нижнее основание изображено штриховой линией.
Приняв верхнее и нижнее основания прямоугольника за диаметр цилиндра, рисуют равные эллипсы, при этом в нижнем основании невидимую часть эллипса изображают штриховой линией.
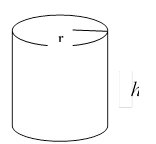
h – высота цилиндра, r – радиус основания
2. При построении конуса:
Надо сначала провести диаметр основания конуса штриховой линией, а затем из его середины провести перпендикуляр – высоту конуса; отметить на перпендикуляре вершину конуса;
Нарисовать в основании эллипс, изображая штриховой линией его невидимую часть. Соединить концы диаметра с вершиной конуса. Если нужно - провести осевое сечение, отметить необходимые по условию задачи элементы.
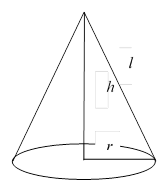
h – высота конуса, r - радиус основания, l - образующая конуса.
3. Наглядным является такое изображение шара, в котором большой круг или любое сечение шара горизонтальной плоскостью изображены в виде эллипсов.
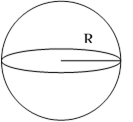
R – радиус шара
Задачи практической работы:
Практическая работа № 32
1 вариант.
1. Осевое сечение цилиндра – квадрат, диагональ которого 20 см. Найти высоту цилиндра и площадь основания цилиндра.
2. Расстояние от центра шара радиуса 14 см до секущей плоскости равно 11 см. Вычислите площадь сечения.
3. Площадь осевого сечения конуса равна 0,6 дм2, высота конуса равна 1,2 дм. Вычислите площадь основания и образующую конуса.
2 вариант.
1. Высота цилиндра равна 12 см, а радиус основания 10 см. Цилиндр пересечён плоскостью, параллельной оси так, что в сечении цилиндра получается квадрат. Найти расстояние от оси цилиндра до секущей плоскости.
2. Расстояние от центра шара радиуса 15 см до секущей плоскости равно 13 см. Вычислите площадь сечения.
3. Угол между образующей и осью конуса равен 45º , образующая равна 6,5 см. Найти площадь боковой поверхности конуса и площадь основания.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 6 |
Геометрия. Многогранники и круглые тела. Измерения в геометрии |
|
|
Тема 6.2 |
Тела и поверхности вращения, их измерения |
|
Практическое занятие №33. Вычисление площадей поверхностей и объемов тел вращения
Учебная цель: применение знаний для вычисления площадей и объемов тел вращения.
Учебные задачи:
1. Знать формулы площадей и объемов фигур.
2. Уметь строить многогранники.
3. Уметь вычислять объемы тел вращения.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
1. Объём
пирамиды вычисляется по формуле: ![]() ,
где S – площадь основания, h -
высота
,
где S – площадь основания, h -
высота
2. Объём конуса вычисляется по формуле: ![]() , где S
– площадь основания, h – высота
, где S
– площадь основания, h – высота
3. Объём шара равен:
![]()
![]() R3
R3
Задачи практической работы:
Практическая работа № 33
1 вариант.
1. Апофема правильной четырёхугольной пирамиды равна 3 см, плоский угол при вершине 60º. Найти объём пирамиды.
2. Образующая конуса равна 4 см. а угол при вершине осевого сечения равен 90º . Найти объём конуса.
3. Прямоугольный треугольник, гипотенуза которого равна 12 см, а острый угол 45º , вращается вокруг катета. Найти объём полученного тела вращения.
4. В цилиндр вписан шар радиуса R. Найти отношение объёмов цилиндра и шара.
2 вариант.
1. В правильной четырёхугольной пирамиде боковое ребро составляет с плоскостью основания угол 45º . Сторона основания пирамиды равна 6 см. Найти объём пирамиды.
2. Высота конуса равна диаметру его основания. Определить объём конуса, если его высота равна Н.
3. Прямоугольный треугольник, гипотенуза которого равна 6 см, а острый угол 45º , вращается вокруг катета. Найти объём полученного тела вращения.
4. В сферу вписан цилиндр, диагональ осевого сечения которого составляет с основанием угол α. Найти объём цилиндра, если радиус сферы равен r.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 7 |
Комбинаторика, статистика и теория вероятностей |
|
|
Тема 7.1 |
Элементы комбинаторики |
|
Практическое занятие №34. Решение прикладных задач с использованием понятий и правил комбинаторики
Практическое занятие №35. Биноминальное разложение с использованием треугольника Паскаля
Учебная цель: применение знаний для решения прикладных задач.
Учебные задачи:
1. Знать формулы комбинаторики и биноминального разложения.
2. Уметь решать прикладные задачи.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр. Перестановками из п разных элементов называются соединения, которые состоят из п элементов и отличаются друг от друга только порядком их расположения.
Число перестановок из п элементов обозначают Рп и вычисляют по формуле Рп = п!
п! ( п – факториал ) п! = 1·2·3·4·5·… п
Пример .Сколькими способами можно разместить 12 человек за столом, на котором поставлены 12 приборов?
Решение
Р12 = 12! = 1·2·3·4·5·… 12 = 479 001 600 Ответ: 479 001 600
Опр.
Комбинации из т элементов по п элементов, которые отличаются друг от друга или самими элементами или порядком элементов, называются размещениями.
Обозначаются ![]() и вычисляются
по формуле
и вычисляются
по формуле ![]() ,
, ![]()
![]()
Пример
Сколько существует вариантов распределения трёх призовых мест, если в розыгрыше участвуют 7 команд?
Решение
![]() Ответ:
210 вар
Ответ:
210 вар
Опр.
Сочетаниями называются все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом.
Обозначают ![]() и вычисляют
по формуле
и вычисляют
по формуле ![]()
Пример
Сколькими способами из колоды в 36 карт можно выбрать 2 карты?
Решение
![]()
Ответ: 630 способов
Бином Ньютона
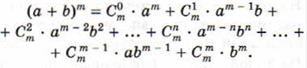
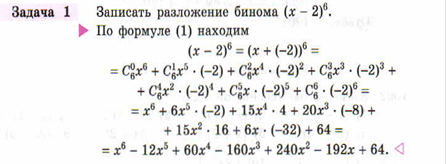
Задачи практической работы:
Практическая работа № 34-35
1 вариант.
1. Вычислить: 1) ![]() ;
2)
;
2) ![]() ; 3)
; 3) ![]()
2. Вычислить: 1) ![]() ;
2)
;
2) ![]()
3. Решить задачи:
1) Сколькими способами можно выбрать для подарка 3 предмета из 9 предметов?
2) В классе 30 человек. Сколькими способами могут быть выбраны из их состава староста и
казначей?
3) Сколькими разными способами можно разместить 6 групп школьников в 6 классных комнатах
(по одной группе в комнате)?
4.
Записать разложение Бинома: ![]()
2 вариант.
1. Вычислить: 1) ![]() ;
2)
;
2) ![]() ; 3)
; 3) ![]()
2. Вычислить: 1) ![]() ;
2)
;
2) ![]()
3. Решить задачи:
1) Сколькими способами можно выбрать для подарка 4 предмета из 8 предметов?
2) Имеются 3 билета на просмотр 3-х различных кинофильмов. Сколькими способами 8 друзей
могут распределить между собой эти 3 билета?
3) Сколькими разными способами можно составить график очерёдности ухода в отпуск 8
сотрудников лаборатории?
4.
Записать разложение Бинома: ![]()
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 7 |
Комбинаторика, статистика и теория вероятностей |
|
|
Тема 7.2 |
Элементы теории вероятностей |
|
Практическое занятие №36. Решение задач на вычисление вероятности события
Практическое занятие №37. Решение прикладных задач с применением вероятностных методов.
Учебная цель: применение знаний для вычисления вероятности событий.
Учебные задачи:
1. Знать формулы вероятности.
2. Уметь решать прикладные задачи.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр. Событие – это любое явление, которое происходит или не происходит или результат испытаний, наблюдений и явлений. События обозначают заглавными латинскими буквами А, В, С, …
Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи.
Долю успеха того или иного события называют вероятностью этого события и обозначают Р(А)
Опр . Если в некотором испытании существует п равновозможных попарно
несовместных исходов и т из них благоприятствуют событию А, то вероятностью
наступления события А называют отношение ![]() и
записывают Р(А) =
и
записывают Р(А) = ![]()
Пример Найти вероятность появления при одном бросании игральной кости числа очков, большего 4.
Решение : А – « появление числа очков, большего 4» п = 6 - число всех
исходов, т = 2 – благоприятствующих событию А ( 5, 6 ) Р(А) = ![]() =
= ![]() Ответ:
Р(А) =
Ответ:
Р(А) = ![]() =
= ![]()
Опр. Суммой (объединением)
двух событий A и B (обозначается A+B,
A![]() B) называется такое событие,
которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B,
или оба одновременно.
B) называется такое событие,
которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B,
или оба одновременно.
Пример
В коробке лежат 8 зеленых, 7 синих и 15 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет, синим или зеленым.
Решение:
А: взяли синий карандаш
В: взяли зеленый карандаш
С: взяли синий или зеленый карандаш
Событие С равно сумме событий А и В: С = А + В
Вероятность события А равна ![]()
Вероятность события В равна ![]()
Вероятность события С равна ![]()
Опр. Произведением (пересечением) двух событий A и B (обозначается A×B, A и B) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Пример
В одной коробке находится 4 белых и 8 черных шаров, а в другой – 3 белых и 9 черных. Из каждой коробки вынули по шару. Вычислить вероятность того, что оба шара окажутся белыми.
Решение:
А: из первой коробки вынули белый шар
В: из второй коробки вынули белый шар
С: из коробок вынули белые шары
Вероятность события А равна ![]()
Вероятность события В равна ![]()
Вероятность события С равна ![]()
Ответ: Р ( С ) ![]() 0,083
0,083
Задачи практической работы:
Практическая работа № 36-37
1 вариант.
1. Среди 170 деталей, изготовленных на станке, оказалось 8 деталей, не отвечающих стандарту. Найдите вероятность выбора детали, не отвечающей стандарту.
2. Контролёр, проверяя качество 500 изделий, установил, что 10 из них относится ко 2-му сорту, а остальные к 1-му. Найдите вероятность: а) выбора изделия 1-го сорта; б) выбора изделия 2-го сорта.
3. Какова вероятность того, что сумма очков, выпавших на 2-х брошенных костях, равна 6 ?
4. На складе имеется 50 деталей, изготовленных тремя бригадами. Из них 25 изготовлено первой бригадой, 15- второй и 10 – третьей. Найти вероятность того, что на сборку поступила деталь, изготовленная второй или третьей бригадой.
5. Игральную кость бросают трижды. Какова вероятность того, что ни разу не выпадет цифра 5?
6. Из колоды карт (36 листов ) наугад вынимается одна карта. Какова вероятность того, что эта карта: 1) валет; 2) король чёрной масти; 3) с чётным числом красной масти; 4) не с числом?
7. Брошены 3 монеты: копейка, пятак и 10 гривенник. Какова вероятность того, что: 1) на копейке появится орёл, а на пятаке и гривеннике – решки; 2) на всех монетах выпадут решки?
2 вариант.
1. Пусть имеется 80 деталей, среди которых 60 исправных, а 20 бракованных. Найти вероятность того, что взятая наугад деталь окажется исправной.
2. В партии из 100 деталей имеется 5 бракованных. Определить вероятность того, что взятая на удачу деталь окажется стандартной.
3. Какова вероятность того, что сумма очков, выпавших на 2-х брошенных костях, равна 5 ?
4. В коробке находятся 250 лампочек, из них 100 по 100 Вт, 50 - по 60 Вт, 50 – по 25 Вт и 50 – по 15 Вт. Вычислить вероятность того, что мощность любой взятой наугад лампочки не превысит 60 Вт.
5. Игральную кость бросают трижды. Какова вероятность того, что ни разу не выпадет цифра 6?
6. Из колоды карт (36 листов ) наугад вынимается одна карта. Какова вероятность того, что эта карта: 1) валет; 2) король чёрной масти; 3) с чётным числом красной масти; 4) не с числом?
7. Брошены 3 монеты: копейка, пятак и 10 гривенник. Какова вероятность того, что: 1) на копейке появится орёл, а на пятаке и гривеннике – решки; 2) на всех монетах выпадут решки?
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
|
Раздел 7 |
Комбинаторика, статистика и теория вероятностей |
|
|
Тема 7.3 |
Элементы математической статистики |
|
Практическое занятие №38. Графическое представление числовых данных: таблицы, диаграммы, графики. Знакомство со встроенными функциями Excel для нахождения основных характеристик выборки. Решение задач на выборку: графическое представление и нахождение основных характеристик.
Учебная цель: применение знаний для решения задач на выборку.
Учебные задачи:
1. Уметь представлять числовые данные.
2. Уметь решать задачи на выборку.
Краткие
теоретические и учебно-методические материалы
по теме практической работы
Опр.
Случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая.
Опр.
Функция, связывающая значения случайной величины с соответствующими им вероятностями, называется законом распределения дискретной случайной величины.
Опр.
Полигоном частот называют зависимость, выражающую распределение величины Х по частотам или по относительным частотам.
Характеристики случайной величины:
Опр.
Размах ( обозначается R ) - разница между наибольшим и наименьшим значениями случайной величины.
Опр.
Мода ( обозначается Мо ) – наиболее часто встречающееся значение случайной величины.
Опр.
Медиана ( обозначается Ме ) – это так называемое серединное значение упорядоченного ряда значений случайной величины.
Пример
В детском обувном магазине за декаду было куплено 750 пар обуви. Кладовщик проводил статистическое исследование и с этой целью записывал размеры каждой пятой из затребованных пар. Эти числа составили следующий ряд данных: 23, 24, 16, 21, 18, 17, 20, 23, 18, 16, 19, 18, 22, 19, 21, 17, 24, 15, 23, 19, 16, 22, 18, 24, 19, 17, 22, 19, 15, 23, 21, 23, 19, 23, 17, 22,16, 19, 22, 18, 20, 15, 21, 23, 19, 18, 23, 22, 20, 17, 19, 23, 21, 24, 22, 23, 20, 22, 21, 18, 16, 19, 22, 23, 20, 24, 21, 19, 24, 16, 20, 23, 24, 18 22, 17, 15, 21, 24, 20, 19, 17, 21, 20, 15, 23, 24, 18, 16, 22, 23, 24, 21, 15, 23, 22, 20, 23, 19, 20, 17, 22, 19, 20, 24, 15, 23, 18, 22, 23, 15, 21, 24, 19, 18, 19, 17, 15, 19, 23, 20, 17, 22, 23, 20, 18, 22, 19, 20, 18, 19, 24, 18, 16, 21, 24, 17, 15, 20, 22, 21, 24, 22, 18, 22, 18, 24, 15, 21.
а) Постройте таблицу частот.
б) Определите моду ряда (самый распространенный размер).
в) Постройте диаграмму частот.
г) Найдите средний размер по этой выборке.
Решение.
а) Сначала при просмотре всей выборки выясним, какие в ней встречаются размеры, и расположим их в порядке возрастания: 15, 16, 17, 18, 19, 20, 21, 22, 23, 24. Далее подсчитаем количество пар каждого размера в выборке (т.е. частоту появления каждого размера) и сведем данные в таблицу
|
Размер обуви |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
Частота |
12 |
8 |
11 |
16 |
19 |
15 |
14 |
19 |
20 |
16 |
б) Мода данного ряда – число 23.
в) Воспользуемся данными таблицы для построения диаграммы частот, в которой по горизонтальной оси отложены номера имеющихся размеров, по вертикальной оси – количество пар каждого размера.
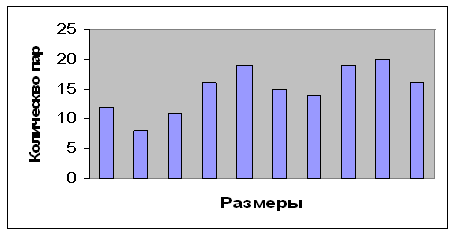
г) Найдем средний размер. Для этого сначала вычислим сумму всех членов ряда: 15 ·12 + 16 · 8 + 17· 11 + 18 · 16 + 19 · 19 + 20 · 15 + 21 · 13 + 22 · 19 + 23 · 20 + 24 ·16 = 3000, затем общее количество членов ряда. Это удобно сделать, сложив частоты: 12 + 8 + 11+ +16 + 19 + 15 + 14 + 19 + 20 + 16 = 150, далее, разделив первый результат на второй, получим средний размер: 3000 / 150= 20.
Задачи практической работы:
Практическая работа № 38
1 вариант.
1. На стол одновременно бросают два игральных тетраэдра, грани каждого из которых пронумерованы числами 1, 2, 3, 4. Составить таблицу распределения по вероятностям значений случайной величины Х – суммы очков на гранях тетраэдров, касающихся поверхности стола.
2. В таблице приведены размеры одежды 50 учащихся 10 класса. На основании этих данных составить таблицу распределения по вероятностям значений случайной величины Х – размеров одежды учащихся 10 класса. Составить таблицы распределения по частотам (М) и относительным частотам (W)
|
50 |
40 |
44 |
44 |
46 |
46 |
44 |
48 |
46 |
44 |
|
38 |
44 |
48 |
50 |
40 |
42 |
50 |
46 |
54 |
44 |
|
42 |
42 |
52 |
44 |
46 |
38 |
46 |
42 |
44 |
48 |
|
46 |
48 |
44 |
40 |
52 |
44 |
48 |
50 |
46 |
46 |
|
48 |
40 |
46 |
42 |
44 |
50 |
46 |
44 |
46 |
48 |
3. Построить полигон частот и полигон относительных частот значений случайной величины Х, распределение которой представлено в таблице:
|
Х |
11 |
12 |
13 |
14 |
15 |
|
М |
3 |
1 |
5 |
6 |
5 |
4. Найти размах, моду и медиану выборки:
1, 3, -2, 4, -2, 0, 2, 3, 1, -2, 4
Построить полигон частот значений величины и указать на нём размах, моду и медиану.
Практическая работа № 37.
Тема: Решение практических задач с применением вероятностных методов.
Цель: Закрепление полученных знаний.
2 вариант.
1. На стол одновременно бросают игральный кубик и игральный тетраэдр (грани которого пронумерованы числами 1, 2, 3, 4). Составить таблицу распределения по вероятностям значений случайной величины Х – суммы очков, выпавших на кубике и грани тетраэдра, касающейся поверхности стола.
2. В таблице приведены размеры одежды 50 учащихся 10 класса. На основании этих данных составить таблицу распределения по вероятностям значений случайной величины Х – размеров одежды учащихся 10 класса. Составить таблицы распределения по частотам (М) и относительным частотам (W)
|
42 |
42 |
52 |
44 |
46 |
38 |
46 |
42 |
44 |
48 |
|
48 |
40 |
46 |
42 |
44 |
50 |
46 |
44 |
46 |
48 |
|
50 |
40 |
44 |
44 |
46 |
46 |
44 |
48 |
46 |
44 |
|
46 |
48 |
44 |
40 |
52 |
44 |
48 |
50 |
46 |
46 |
|
38 |
44 |
48 |
50 |
40 |
42 |
50 |
46 |
54 |
44 |
3. Построить полигон частот и полигон относительных частот значений случайной величины Х, распределение которой представлено в таблице:
|
Х |
23 |
24 |
25 |
26 |
27 |
28 |
|
М |
6 |
5 |
2 |
3 |
1 |
3 |
4. Найти размах, моду и медиану выборки:
0,2 ; 0,4; 0,1; 0,5; 0,1; 0,2; 0,3; 0,5; 0,4; 0,6
Построить полигон частот значений величины и указать на нём размах, моду и медиану.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
Практическое занятие №39. Итоговое повторение.
Учебная цель: закрепление полученных знаний.
Назначение работы – определение соответствия содержания и качества подготовки студентов 1 курса федеральному государственному образовательному стандарту по математике.
Задачи практической работы:
Практическая работа № 39
1.
Даны три вектора: ![]()
![]() ;
; ![]() ,
где
,
где
А(-1,1,-3), В(0,-2,-4). Какие из этих векторов равны?
1) Только ![]() и
и ![]() ; 2)
Только
; 2)
Только ![]() и
и ![]() ; 3)
Только
; 3)
Только ![]() и
и ![]() ;
;
4) Все равны; 5) Равных нет.
2.
Даны три вектора: ![]() ;
;![]() ;
;![]() , где
, где
А(2,-2,4), В(1,3,2). Какие из этих векторов коллинеарны?
1) Только ![]() и
и ![]() ; 2)
Только
; 2)
Только ![]() и
и ![]() ; 3)
Только
; 3)
Только ![]() и
и ![]() ;
;
4) Все коллинеарны; 5) Коллинеарных нет.
3.
Если ![]() , то
, то ![]() =…
=…
1) ![]() ; 2) 7; 3)
13; 4)
; 2) 7; 3)
13; 4) ![]() ; 5)
11.
; 5)
11.
4.
Найдите значение выражения:![]()
а) 2,5; б) 1,25; в) 1,75; г) 1,5.
5. Упростите
выражение: ![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
6. Решите уравнение: ![]() .
.
а)
![]() ; в)
; в)
![]() ;
;
б)
![]() ; г)
; г) ![]() .
.
7.
Решите неравенство: ![]()
а)
![]() ; в)
; в)
![]() ,
,![]() ;
;
б)
![]() ,
,![]() ; г)
; г)
![]() ,
,![]() .
.
8. Известны первые
три члена числовой последовательности: ![]() .
Тогда формула общего члена этой последовательности имеет вид…
.
Тогда формула общего члена этой последовательности имеет вид…
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4)
![]() .
.
9. Производная частного ![]() равна…
равна…
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
10. Найдите
производную функции ![]() .
.
|
1) |
|
|
3) |
|
11. Вычислите значение производной функции у = sin x – 2х в точке х0 = 0.
|
1) |
1 |
2) |
0 |
3) |
–3 |
4) |
–1 |
12. Неопределенный интеграл – это…
1) числовой интервал; 2) уравнение; 3) совокупность функций; 4) число; 5) функция.
13. Чему равен неопределенный интеграл ![]() ?
?
1) ![]() ; 2)
; 2)
![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
14. Интеграл ![]() равен…
равен…
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
15. Вычислить определенный интеграл ![]()
1) 4,125; 2) 3,625; 3) 3,375; 4) 3,125.
16. Из каждой из двух колод вынимают по одной карте. События А - <<карта из первой колоды - красной масти>> и В - <<карта из второй колоды бубновой масти>> являются...
1) несовместными и зависимыми; 2) совместными и зависимыми;
3) совместными и независимыми; 4) несовместными и независимыми.
17. В ящике 25 деталей, из которых 9 бракованных. Сборщик наугад достает 3 детали. Какова вероятность того, что все три не бракованные?
1) 28/115; 2) 8/23; 3) 16/91; 4) 40/133.
18. Игральную кость бросают 5 раз. Вероятность того, что ровно 2 раза выпадет грань с четным числом очков, равна...
1) 5/16; 2) 1/32; 3) 7/64; 4) 1/4.
19. Дан закон распределения дискретной случайной величины Х
|
|
1 |
2 |
3 |
4 |
|
|
0,1 |
а |
0,2 |
0,6 |
Тогда значение а равно...
1) 0,1; 2) -0,9; 3) 0,2; 4) 0,9.
20. Из генеральной совокупности извлечена выборка объема n = 50
|
|
|
2 |
3 |
4 |
|
|
|
9 |
8 |
7 |
Тогда равен…
1) 50; 2) 26; 3) 27; 4) 10.
Образовательные результаты, заявленные в ФГОС и обеспеченность занятия (средства обучения) см. Приложение 1.
Приложение 1.
Образовательные результаты, заявленные в ФГОС
|
Результаты обучения |
Критерии оценки |
Методы оценки |
|
Личностные: |
|
|
|
Развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования |
Анализирует результаты своих действий, вносит коррективы. Подбирает разные алгоритмы работы с информацией
|
Экзамен
|
|
Овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественнонаучных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки |
Выбирает простые и эффективные способы решения задач. Обладает знанием базовых алгоритмов решения задач
|
Наблюдение за соблюдением алгоритма выполнения задания
|
|
Готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности |
Запрашивает обратную связь у преподавателя и (или) однокурсников. Демонстрирует интерес к изучению тем на более углубленном уровне
|
Наблюдение за соблюдением алгоритма выполнения задания
|
|
Готовность и способность к самостоятельной творческой и ответственной деятельности |
Выбирает простые и эффективные способы решения задач. Подбирает разные алгоритмы работы с информацией Работает самостоятельно |
Наблюдение за деятельностью обучающихся в малых группах (в ситуациях сотрудничества) |
|
Готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности |
Быстро находит общий язык с группой. Выстраивает конструктивные взаимоотношения. Сглаживает конфликты
|
Наблюдение за деятельностью обучающихся в малых группах (в ситуациях сотрудничества). Оценка защиты проекта |
|
Метапредметные: |
|
|
|
Умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях |
Выбирает оптимальные средства для выполнения работы. Разбивает выполнение сложной задачи на этапы. Критически оценивает информацию из разных источников
|
Оценка подготовки и защиты проекта
|
|
Готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников |
Критически оценивает информацию из различных источников. Решает задачи прикладного характера (физика, химия, механика)
|
Оценка подготовки и защиты проекта. Наблюдение за соблюдением алгоритма выполнения задания |
|
Владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
|
Логично и точно поясняет решение задачи, аргументированно излагает свою точку зрения на применяемый алгоритм решения |
Наблюдение за соблюдением алгоритма выполнения задания |
|
Владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения |
Ведет самостоятельное наблюдение за своей деятельностью, своевременно устраняет ошибки. Выбирает оптимальные средства для выполнения работы. Запрашивает обратную связь у преподавателя и однокурсников |
Наблюдение за соблюдением алгоритма выполнения задания |
|
Предметные: |
|
|
|
Сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке; |
Демонстрирует знание основных
математических методов решения прикладных задач;
|
Наблюдение и оценка результатов работы студентов на практических занятиях (работа в парах и группах, фронтальный опрос и индивидуальная беседа, при развёрнутом ответе у доски) |
|
Владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач |
Аргументирует решение задачи
|
Наблюдение за соблюдением алгоритма выполнения задания Экзамен |
|
Владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств |
Определяет вид уравнения и неравенства, применяет аналитический и графический методы их решения; использует методы решения систем уравнений и неравенств для построения моделей прикладных задач и интерпретации их решений
|
Оценка выполнения расчётно-графической работы. Экзамен |
|
Сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей |
Имеет представление об основных понятиях интегрального и дифференциального исчисления, поясняет их определениями и формулами; решает прикладные задачи с использованием элементов дифференциального и интегрального исчислений; определяет вид функции, находит область определения и область значений, строит график функции |
Оценка выполнения расчётно-графической работы. Экзамен
|
|
Владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием |
Имеет понятие о плоских и пространственных фигурах (виды многогранников и круглых тел, их сечения), распознаёт многогранники и круглые тела на чертежах (схематично выполняет их построение) и в реальном мире; применяет основные свойства и формулы для нахождения элементов и измерений пространственных фигур. |
Оценка выполнения расчётно-графической работы. Экзамен
|
|
Сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин; |
Решает задачи на вычисление вероятности с использованием элементов комбинаторики. Находит основные характеристики случайных величин и интерпретирует их вероятностный смысл
|
Оценка выполнения практической работы. Экзамен
|
|
Владение навыками использования готовых компьютерных программ при решении задач |
Применяет статистический пакет Excel при работе на ПК с числовыми массивами данных |
Оценка выполнения практической работы |
Материально-техническое обеспечение
Оборудование:
– посадочные места по количеству обучающихся;
– рабочее место преподавателя;
– наглядные пособия (комплекты учебных таблиц, плакатов, портретов выдающихся ученых-математиков и др.); чертежные инструменты, модели фигур, стереометрических тел, набор планиметрических фигур.
– измерительные инструменты: линейка, транспортир, циркуль.
– многофункциональный комплекс преподавателя;
– информационно-коммуникативные средства;
– экранно-звуковые пособия;
– комплект технической документации, в том числе паспорта на средства обучения, инструкции по их использованию и технике безопасности;
– библиотечный фонд.
Информационное обеспечение
Печатные издания
1. Колягин Ю.М. Алгебра и начала математического анализа. 10 кл. Учебник базового и углубленного уровня. М.: Просвещение, 2018. – 358с.
2. Колягин Ю.М. Алгебра и начала математического анализа. 11 кл. Учебник базового и углубленного уровня. М.: Просвещение, 2017. – 358с.
Электронные источники (электронные ресурсы)
1. Электронно-библиотечная система IPRbooks [Электронный ресурс] : режим доступа www.iprbookshop.ru , свободный.
2. Информационные, тренировочные и контрольные материалы [Электронный ресурс]: режим доступа www.fcior.edu.ru , свободный
3. Единая коллекции цифровых образовательных ресурсов [Электронный ресурс]: режим доступа www.school-collection.edu.ru , свободный.
4. Издательский центр «Академия» : режим доступа http://www.academia-moscow.ru.
Дополнительные источники
1. Алимов Ш.А. Алгебра и начала математического анализа. 10-11 классы: Учеб. Для общеобразоват. учреждений. М.: Просвещение, 2011. – 464с.
2. Атанасян Л.С. Геометрия. 10-11классы. Учеб. для общеобразоват. учрежд. М.: Просвещение, 2012. – 255с.
3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017.
4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017.
5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб-метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017.
6. Башмаков М.И., Цыганов Ш.И. Методическое пособие для подготовки к ЕГЭ.–М., 2014.
7. Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.