Выполнение лабораторной работы по математике «Статистическое обоснование пиксельным методом формулы площади квадрата Sₐₓₐ = a²»

Выполнение лабораторной работы по математике, разработанной Бодряковым В.Ю. и Быковым А.А. [1, 52 с.]

ОТЧЕТ

по Лабораторной работе по математике (ЛРМ3)

Ф.И.О.: Москалев Иван Сергеевич, учитель информатики ГКОУ СО «Екатеринбургская ВШ № 2»

Тема: «Статистическое обоснование пиксельным методом формулы площади квадрата Sₐₓₐ = a², "a > 0».

Цель: Статистически обосновать пиксельным методом формулы площади квадрата Sₐₓₐ = a²,"a > 0.

Задачи:

1.      Освоить пиксельный метод обоснования формул для вычисления площадей геометрических фигур;

2.      Разработать алгоритм выполнения работы;

3.      Установить справедливость формулы площади квадрата Sₐₓₐ = a²,"a > 0;

4.      Подготовить отчет по ЛРМ.

Гипотеза: формула площади квадрата Sₐₓₐ = a² справедлива.

Оборудование и материалы: персональный компьютер с установленным ПО MS Office.

1° Теория.

Действительно, если число a выражается натуральным числом (a  ℕ), то очевидно, что S□ = a². В этом можно удостовериться просто пересчитав клетки единичной длины, целиком заполняющие такой квадрат; число клеток равно a·a = a². Площадь единичной клетки признаем равной S□1 = 1.

            Однако необходимо уже доказывать, что если сторона квадрата выражается рациональным числом (a  ℚ, т.е. a = m/n, где m, n  ℕ), то по-прежнему справедлива формула S□ = a². Авторы различных учебников по геометрии решают эту проблему по-разному [1].

Пиксельный подход, по сути, является современной и легко «цифровизуемой» реализацией фундаментального математического понятия «мера множества» на числовой плоскости, адаптированного к уровню, доступному для понимания школьниками и их учителями. Под пикселем понимается некоторый малый единичный элемент («квант») пространства на плоскости; площадь пикселя принимается равной единице. Предполагается, что все доступное пространство (пиксельное поле) может быть замощено пикселями – без пробелов и без наложений. Примером пикселя на плоскости может служить клетка в школьной тетради в клетку. Именно так и будем его понимать в дальнейшем, – для наглядности.

Применительно к задаче об оценке площади квадрата с произвольной действительной стороной a > 0, уместно поступить следующим образом. Разместим на сетчатом координатном поле (странице школьной тетради в клетку) квадраты со случайными сгенерированными сторонами.

Очевидно,

[a] ≤ a < [a] + 1,

где [a] – целая честь действительного числа a. Отсюда

[a]² ≤  S_□ < ([a] + 1)².

            Для последующего построения корреляционной зависимости S_□ vs. a² удобно использовать физическую нотацию:

S_□ = <S_□> ± δS_□,

где

<S_□> =  (([a] + 1)² + [a]²) = [a]² + [a] + ;

δS_□ =   (([a] + 1)² – [a]²) = [a] + .

Основная статистическая гипотеза, которая должна быть проверена:

H₀: S_□ = ka², "a > 0, где k ≡ 1.

            Конкурирующая гипотеза:

H₁: S_□ = ka², где k ≠ 1.

            Для проверки основной гипотезы необходимо изучить корреляционную зависимость S_□ vs. a², аппроксимировав множественные «экспериментальные» данные линейным трендом, проходящим через нуль.

Таким образом, если k ≡ 1 и, следовательно, для площади любого квадрата справедлива привычная формула S_□ = a², "a > 0.

2° Ход работы.

1.      Сгенерировать 1000 случайных чисел а;

2.   Составить таблицу и внести в нее результаты вычислений: [a]²; [a+1]²; a²; ;

3.      Составить корреляционную диаграмму исходя из полученных данных a² и S_ср;

4.   Провести обработку данных, определить наклон линии тренда, если он 45,то формула площади квадрата верна.

3° Результаты и обсуждение.

Рассмотрим некоторую часть полученных результатов

Диаграмма:

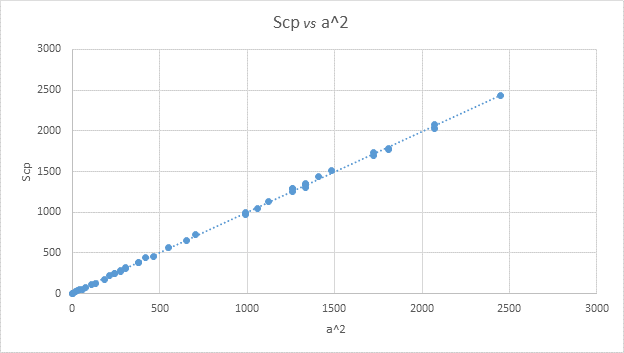
По диаграмме видно, что угол 45 k1 (k=0,9998), следовательно, можно считать формулу площади квадрата верной.

4° Выводы.

В пределах статистической погрешности по 10-ти определениям углового коэффициента k по 100 точкам на корреляционной диаграмме ‹S› vs. a², «экспериментально» измеренное значение k = 0,9998 согласуется с точным k = 1. Цель достигнута, задачи выполнены.

1)         Будет ли такая ЛРМ способствовать эффективному формированию функциональной математической грамотности обучающихся?

Данная ЛРМ формирует функциональную математическую грамотность, так как обучающиеся учатся умениям распознавать проявление математических понятий, объектов и закономерностей в реальной жизненных ситуации, создают математические модели, интерпретируют и оценивают полученные результаты.

2)         Какие внутри- и межпредметные связи курса математики реализует выполненная ЛРМ?

Эта ЛРМ связывает математику и информатику.

Также она реализует н внутрипредметную связь: умение строить графики и производить расчеты в MS Excel, а также находить площадь квадрата.

3)         Готовы ли Вы использовать эту ЛРМ при обучении школьников математике?

Да, так как при выполнении данной ЛРМ учащиеся лучше смогут:

•                     понять и запомнить формулу площади квадрата;

•                     развить навыки статистического анализа и обработки данных;

•                     научиться применять теоретические знания на практике;

•                     развить логическое мышление и умение делать выводы;

•                     повысить мотивацию к изучению математики.

4)         В каком классе, с Вашей точки зрения, это делать предпочтительнее всего?

Мы считаем, что лучше эту лабораторную работу проводить в 8 классе, для более глубокого понимания доказательства площади квадрата.

5)         Какие затруднения можно ожидать при выполнении этой ЛРМ обучающимися и как можно преодолеть эти затруднения?

Возможные затруднения при выполнении лабораторной работы:

•                     технические проблемы с оборудованием или программным обеспечением;

•                     сложности в обработке и анализе полученных данных;

•                     трудности в интерпретации результатов и представлении их в виде отчёта.

Для преодоления этих затруднений мы рекомендуем:

•                     провести предварительное обучение работе с оборудованием и программным обеспечением;

•                     предоставить обучающимся доступ к дополнительным материалам и ресурсам для изучения математических методов и формул;

•                     организовать групповые обсуждения и консультации с преподавателями и другими специалистами для обмена опытом и получения обратной связи;

•                     уделить внимание развитию навыков анализа и интерпретации данных, а также составлению отчётов о проделанной работе.

Список литературы:

1.        Бодряков, В.Ю. Сборник лабораторных работ по математике : учебное пособие для вузов / В. Ю. Бодряков, А.А. Быков. – Санкт-Петербург : Лань, 2023. – 78 стр.: ил. – Текст непосредственный.

2.        Бодряков В.Ю., Быков А.А. Улучшаемые пиксельные оценки мер плоских множеств как методический подход к введению понятия "Площадь фигуры" в курсе геометрии. Часть 1 // Математическое образование. 2019. № 4 (92). С. 17-29.

3.        Бодряков В.Ю., Быков А.А. Улучшаемые пиксельные оценки мер плоских множеств как методический подход к введению понятия "Площадь фигуры" в курсе геометрии. Часть 2 // Математическое образование. 2020. № 1 (93). С. 15-23.

4.        Скачано с www.znanio.ru