ФИЗИЧЕСКАЯ ЭЛЕКТРОНИКА

 

Лекция. Физические основы эмиссионной электроники

Термоэлектронная эмиссия металлов и полупроводников. Работа выхода.

Закон Ричардсона-Дешмана. Контактная разность потенциалов. 

Литература: 

Обязательная:

1.     А.М. Бродский, Ю.Я. Гуревич Теория электронной эмиссии из металлов. М.: Наука, 1973

2.     К. Шимони Физическая электроника.  пер. с нем.Москва.: Энергия, 1977, 608 с.

Дополнительная

1.     Л.Н.Добрецов, М.В. Гамаюнова Эмиссионная электроника.      1966. 

2.     C.К.Жданов, В.А.Курнаев, М.К. Романовский, И.В.Цветков Основы

физических процессов в плазме и плазменных установках: Учеб. пособие /

Москва: МИФИ, 2000. 184 с.

 

Лекция. Физические процессы, сопровождающие эмиссию. Эффект Шоттки. Автоэлектронная эмиссия. 

Литература: 

Обязательная:

1.     А.М. Бродский, Ю.Я. Гуревич Теория электронной эмиссии из металлов. М.: Наука, 1973

2.     К. Шимони Физическая электроника.  пер. с нем.Москва.: Энергия, 1977, 608 с.

Дополнительная

1.     Л.Н.Добрецов, М.В. Гамаюнова Эмиссионная электроника.      1966. 

2.     C.К.Жданов, В.А.Курнаев, М.К. Романовский, И.В.Цветков Основы

физических процессов в плазме и плазменных установках: Учеб. пособие / Москва: МИФИ, 2000. 184 с.

 

Лекция. Вакуумный диод. Уравнение Чайлда-Ленгмюра. Физические явления в вакуумном диоде. 

Литература: 

Обязательная:

1. К. Шимони Физическая электроника.  пер. с нем. Москва.: Энергия, 1977, 608 с.

Дополнительная

1. C.К.Жданов, В.А.Курнаев, М.К. Романовский, И.В.Цветков Основы

физических процессов в плазме и плазменных установках: Учеб. пособие /

Москва: МИФИ, 2000. 184 с.

 

Лекция. Фотоэлектронная эмиссия. Основные законы. Формула Фаулера. Фотокатоды.

Литература: 

Обязательная:

1. К. Шимони Физическая электроника.  пер. с нем.Москва.: Энергия, 1977, 608 с.

Дополнительная

1. C.К.Жданов, В.А.Курнаев, М.К. Романовский, И.В.Цветков Основы

физических процессов в плазме и плазменных установках: Учеб. пособие /

Москва: МИФИ, 2000. 184 с.

 

Лекция. Вторичная электронная эмиссия. Распределение вторичных электронов по энергиям. Зависимость коэффициента вторичной эмиссии от энергии и угла падения первичных электронов. Вторично-электронные эмиттеры. Другие виды эмиссии.

 

Литература: 

Обязательная:

1. К. Шимони Физическая электроника.  пер. с нем.Москва.: Энергия, 1977, 608 с.

Дополнительная

1. C.К.Жданов, В.А.Курнаев, М.К. Романовский, И.В.Цветков Основы физических процессов в плазме и плазменных установках: Учеб. пособие /

Москва: МИФИ, 2000. 184 с

 

Лекция. Экспериментальные методы изучения эмиссионных характеристик. Эмиссионные материалы для термокатодов (металлические, активированные, оксидные).Фотокатоды.

Литература: 

Обязательная:

1. К. Шимони Физическая электроника.  пер. с нем.Москва.: Энергия, 1977, 608 с.

Дополнительная

1. C.К.Жданов, В.А.Курнаев, М.К. Романовский, И.В.Цветков Основы физических процессов в плазме и плазменных установках: Учеб. пособие /

Москва: МИФИ, 2000. 184 с

 

 

Лекция. Движение заряженных частиц в статических электрическом и магнитном полях. Модифицированные уравнения движения в аксиальносимметричных полях.

Литература: 

Обязательная:

1. Л.А.Арцимович, С.Ю.Лукьянов Движение заряженных частиц в электрических и магнитных полях. Учебное пособие, Изд.2-ое, М.:

Наука, 1978. 224 с.

Дополнительная

1.            П. Хокс, Э. Каспер Основы электронной оптики в 2-х т. Т.2 М.: Мир,

1993. 480 с.

 

Лекция. Элементы электронной оптики. Электростатические и магнитнитостатические фокусирующие системы. Электронный микроскоп.

АСМ.

Литература: 

Обязательная:

1. Л.А.Арцимович,      С.Ю.Лукьянов    Движение     заряженных     частиц      в

электрических и магнитных полях. Учебное пособие, Изд.2-ое, М.: Наука, 1978. 224 с.

Дополнительная

1. П. Хокс, Э. Каспер Основы электронной оптики в 2-х т. Т.2 М.: Мир,

1993. 480 с

 

Лекция. Движение потоков заряженных частиц. Особенности движения потоков заряженных частиц. Учет кулоновского поля. Эмиттанс. Яркость.

Ленгмюровский предел плотности тока.

Литература: 

Обязательная:

1.     С.И. Молоковский, А.Д. Сушков Интенсивные электронные и ионные пучки М.: Энергоатомиздат, 1991, 304 с.

2.     П. Хокс, Э. Каспер Основы электронной оптики в 2-х т. Т.2 М.: Мир, 1993. 480 с.

Дополнительная

1.     Дж.Лоусон Физика пучков заряженных частиц.М.: Мир , 1980. 438 с.

2.     Е.А.Абрамян, и др. Интенсивные электронные пучки Энергоатомиздат, 1984

 

Лекция. Предельная плотность тока пучка в  вакуумном  и газовом пролетном промежутке. Влияние ионов на процесс транспортировки пучка.

Процесс рассеяния на молекулах фонового газа.

Литература: 

Обязательная:

1.     С.И. Молоковский, А.Д. Сушков Интенсивные электронные и ионные пучки М.: Энергоатомиздат, 1991, 304 с.

2.     П. Хокс, Э. Каспер Основы электронной оптики в 2-х т. Т.2 М.: Мир, 1993. 480 с.

Дополнительная

1.     Дж.Лоусон Физика пучков заряженных частиц.М.: Мир , 1980. 438 с.

2.     Е.А.Абрамян, и др. Интенсивные электронные пучки Энергоатомиздат, 1984

 

Лекция.    Элементы    ионной    оптики.    Статические    масс-анализаторы.

Динамические масс-анализаторы.

Литература: 

Обязательная:

1. К. Шимони Физическая электроника.  пер. с нем.Москва.: Энергия, 1977,

608 с

Дополнительная

1. Л.Н. Розанов Вакуумная техника. Москва.: Высшая школа, 1990. 320 с

 

Лекция. Методы экспериментального изучения параметров пучков.

Цилиндр Фарадея. Пояс Роговского. Энергетический анализ.

Литература: 

Обязательная:

1. С.И. Молоковский, А.Д. Сушков Интенсивные электронные и ионные пучки М.: Энергоатомиздат, 1991, 304 с 

Дополнительная

1. Е.А.Абрамян, и др. Интенсивные электронные пучки Энергоатомиздат, 1984

 

Лекция. Взаимодействие пучков заряженных частиц с  веществом Электронно-лучевая технология. Ионная обработка материалов.  

Литература: 

Обязательная:

1. А.Н.Диденко, А.Е.Лигачев, И.Б.Куракин Воздействие пучков заряженных частиц на поверхность металлов и сплавов. М.: Энергоатомиздат, 1987.

184 с.

Дополнительная

1. Е.А.Абрамян, и др. Интенсивные электронные пучки Энергоатомиздат, 1984

 

 

ЛАБОРАТОРНЫЕ РАБОТЫ ПО КУРСУ:

 

 

Вакуумная электроника:

•      «Определение эмиссионных констант вольфрамового катода и закона распределения эмитированных электронов по скоростям» 

•      «Вакуумный диод»

•      «Электронная пушка и ее характеристики»

•      «Определение характеристик электронного инжектора»

•      «Определение характеристик элементов электронной оптики»

•      «Фотоэмиссия. Спектральная чувствительность ФЭУ» 

•      «Основы масс-спектрометрии»

  

Аннотация:

Изучаются закономерности термоэлектронной эмиссии методом вольтамперных характеристик. Элементы электронной и ионной оптики.

Литература:

Обязательная:

1.     К. Шимони Физическая электроника.  пер. с нем.Москва.: Энергия,

1977, 608 с

2.     С.И. Молоковский, А.Д. Сушков Интенсивные электронные и ионные пучки М.: Энергоатомиздат, 1991, 304 с.

Дополнительная: 

1.     Специальный физический практикум Ч.2, изд.3 под ред. А.А.Харламова Учеб. пособие / Москва.: Издательство МГУ, 1977, 376с.

2.     C.М.Левитский Сборник задач и расчетов по физической электронике :

Изд. Киевского ун-та, 1964.211с.

 

 

Примерный перечень тем курсовых работ и контрольных практических заданий.

Курсовые работы:

•       Плазменный инжектор Лизитано.

•       Электронный инжектор на основе катода LaB6.

•       Изучение энергетического          спектра      электронов         методом задерживающего потенциала.

•       Система диагностики пучка инжектора (Цилиндр Фарадея. Пояс Роговского.).

•       Резонаторный блок малогабаритного авторезонансного ускорителя.

•       Расчет      системы    высадки    пучка         на     твердотельную мишень

резонансного ускорителя.

•       Спектрометрия тормозного излучения ЭЦР источника плазмы.

•       Калибровка рентгеновского спектрометра.

 

Контрольные практические задания:

•       Комптон эффект

•       Магнитный анализ частиц

•       Измерение контактной разности потенциалов между полупроводниками

•       Изучение влияния пространственного заряда на вольт-амперную характеристику термотока

•       Изучение термоэлектронной эмиссии при малых плотностях эмиссионного тока

•       Исследование внешнего фотоэффекта

•       Исследование внутреннего фотоэффекта

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЭМИССИОННАЯ ЭЛЕКТРОНИКА

 

3.1. Электронная эмиссия

Электроны проводимости свободно перемещаются по всему металлу. Их выходу наружу препятствуют силы, действующие у поверхности металла. В результате разнообразных внешних воздействий происходит процесс испускания электронов в вакуум, когда электрон приобретает энергию, достаточную для преодоления потенциального барьера, существующего на границе вещество-вакуум. В зависимости от типа внешнего воздействия различают следующие основные виды электронной эмиссии:

•     фотоэлектронную эмиссию;

•     термоэлектронную эмиссию; 

•     автоэлектронную эмиссию;   вторичную электронную эмиссию;   ионно-электронную эмиссию. 

Во всех указанных явлениях электронно-эмиссионные свойства вещества определяются, в основном, распределением по энергии свободных электронов. Интенсивная эмиссия — это выход достаточно большого количества электронов в единицу времени через единицу площади поверхности, отделяющей вещество от вакуума.

Металлы являются кристаллическими телами, где электроны, находящиеся на внутренних оболочках, остаются связанными с ядром своего атома, а, слабо связанные валентные электроны, как бы обобществляются,

т.е. оказываются связанными не с конкретными атомами, а со всей системой («электронный газ») и могут, при определенных условиях, квазисвободно перемещаться. Количество частиц, образующих электронный газ, может быть оценено исходя из числа узлов кристаллических решеток в единице объема вещества. Оно составляет величину порядка 10²² – 10²³. Таким образом, с точки зрения интенсивной эмиссии, металлы, являясь

«резервуаром» с большим количеством свободных электронов в единице объема, обладают неоспоримым преимуществом.

Энергетическая диаграмма в модели электрона, находящегося в потенциальной яме, напоминает картину жидкости, налитой в стакан (рис. 3.1а). Дно зоны – дно зоны проводимости. Потенциальная энергия электрона вне металла полагается равной нулю, а внутри металла она отрицательна. Для того чтобы электрон мог покинуть металл, его кинетическая энергия должна быть больше глубины потенциальной ямы U_p. Концентрация электронов, обладающих энергиями в интервале от ε до ε+dε, описывается

                                                                                                                4        3

формулой: dn_ Ff d, где F^ ₃ 2^m_e 2 ^  - функция плотности h

энергетических состояний, f  ^1 exp^^U^{F }^^1- среднее число частиц

                                                                                                          kT   

с данной энергией (распределение Ферми-Дирака), ^U_F  h2 3N32 -

2m8

энергия Ферми (максимальная энергия, которой могут обладать электроны в отсутствие теплового движения). При температуре абсолютного нуля и ε>U_F  в металле нет электронов с энергией больше U_F, а при ε<U_F  dn_  const d (рис. 3.1б). С повышением температуры в распределении частиц появляется небольшая часть электронов, обладающих энергиями, превышающими U_F  (обычно kT<<U_F: при комнатной температуре kT1/40 эВ, U_F — порядка нескольких эВ). Энергию, равную разности между глубиной потенциальной ямы U_p и уровнем Ферми U_F , называют работой выхода электрона из металла и обозначают Φ=eφ (е — заряд электрона, φ - потенциал выхода). При конечных значениях температуры энергетическая граница размывается, и часть электронов с энергией, превышающей работу выхода, может покинуть металл. Этот процесс перераспределения электронов по энергии приводит к возможности замены распределения Ферми-Дирака максвелловским распределением. Например, для вольфрама U_F =8 эВ при температуре Т = 2000 К, представляющей практический интерес (рабочая температура вольфрамового катода), отношение U_F/kT = 40. Для электронов с

энергией, превышающей U_F хотя бы на 10%, величина exp^_^kT^{UF }_1. В этом _

случае в выражении для распределения Ферми-Дирака можно пренебречь

единицей. Тогда  ^dn_const exp^ ^{ }d, что соответствует  kT 

распределению Максвелла. Таким образом, при термоэлектронной эмиссии, катод покидают наиболее быстрые частицы, при этом их распределение можно описывать согласно статистике Максвелла-Больцмана.

 

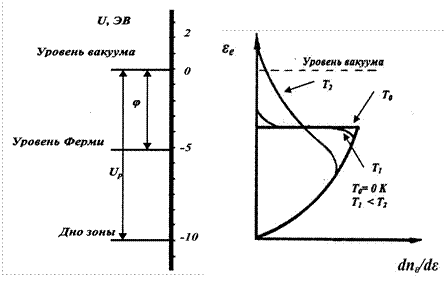
                                                               а                                             б

Рис. 3.1

 

Газокинетическое давление электронного газа внутри металла можно оценить, исходя из средней энергии свободных электронов, которая может быть получена путем усреднения по распределению Ферми-Дирака в 2

пределах от нулевой энергии до уровня Ферми  ^U_F . При плотности 3

электронного газа 10²³ см^-3 и Т=300 К давление составит величину порядка 10⁹ Па. Такое гигантское внутреннее давление не приводит к разрушению кристаллической структуры металла ввиду того, что на границе металл- вакуум существует потенциальный барьер, который препятствует выходу электрона. Его существование обусловлено двумя факторами (рис. 3.2):

•      наличие двойного электрического слоя, образованного граничным рядом узлов кристаллической решетки;

•      уход электрона из металла приводит к наведению в нем положительного заряда.

Высота барьера по порядку величины может быть оценена исходя из выражения: _ ^e , где а – ширина двойного электрического слоя. Таким 2a

образом, полная работа выхода различна не только для разных металлов, но и, в значительной степени, определяется кристаллографической ориентацией грани монокристалла, с которой происходит эмиссия электронов (рис. 3.2).

В таблице приведены значения работы выхода, усредненной по различным кристаллографическим граням, для некоторых металлов:

Металл	Fe	Ba	Ca	Ta	Ni	Mo	W
Работа выхода, эВ	4,25	2,11	2,24	4,07	4,60	4,41	4,52

 

Ввиду того, что толщина двойного слоя по порядку величины совпадает с размерами атома, напряженность поля в слое достигает значений порядка 10⁸В/см, что позволяет уравновесить гигантское внутреннее давление электронного газа.

 

Рис. 3.2

Явление электронной эмиссии из металла будет наблюдаться, если электронам сообщена тем или иным образом энергия, превышающая высоту потенциального барьера. Этот процесс характеризуется плотностью тока

эмиссии. 

 

 

 

3.2. Фотоэлектронная эмиссия

 Явление испускания электронов поверхностью вещества под воздействием электромагнитного излучения называется фотоэлектронной эмиссией или внешним фотоэффектом. Поток электромагнитного излучения, частично проникая внутрь вещества, поглощается в нем и передает энергию электронам проводимости. В случае однофотонной эмиссии (фотон взаимодействует только с одним свободным электроном, отдавая ему полностью свою энергию), явление наблюдается, когда выполнено условие: h h0  , где 0 ^{ c}_0 - пороговая частота падающего электромагнитного излучения, начиная с которой фотон может вырвать электрон из металла, 0 - пороговая длина волны или красная граница фотоэффекта (рис.3.3а). Величина тока насыщения пропорциональна

~

величине светового потока - Ф (рис. 3.3б).

          

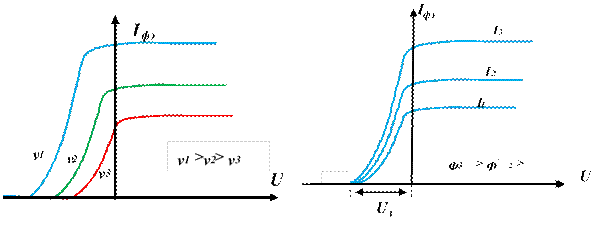
                                              а                                                             б

Рис. 3.3

 

Для внешнего фотоэффекта справедливо уравнение Эйнштейна: h    m_max² / 2, где v_max - максимальная скорость фотоэлектронов, которая связана с задерживающей разностью потенциалов U_З  соотношением m_max² / 2  ^eU_З. Таким образом, задерживающая разность потенциалов U_З связана с частотой  света соотношением: ^U_З  (h/e), где  /e - потенциал работы выхода (рис. 3.4). Продолжение прямой до пересечения с осью ординат определяет потенциал выхода  электронов из металла, а точка пересечения прямой с осью абсцисс дает граничную частоту 0 /h фотоэффекта. Тангенс угла наклона прямой к оси частот tg ^dU_З /d h/^e определяется только постоянной Планка и зарядом

электрона.

Рис. 3.4 

 В таблице представлены экспериментальные значения 0 для различных металлов. Разброс обусловлен тем, что работа выхода зависит от многих факторов: состояние поверхности, химическая чистота материала и др.

Металл	W	Mo	Ta	Na	Ba	Cs
0(мкм)	230-290	280-380	260-300	580-690	540-780	900-1700

 

 Из представленных в таблице данных и графических зависимостей (рис. 3.5), видно, что фотоэмиссия в видимом диапазоне характерна для щелочных металлов.

Законы фотоэффекта, установленные экспериментально и объясненные теоретически на основе фотонной теории света, сводятся к следующим основным положениям:

•  величина фототока насыщения I_фэ пропорциональна величине светового

~

потока -  Ф (Рис. 3.3б);

•  существование длинноволнового порога фотоэффекта (Рис. 3.3а);

•  максимум энергии эмитируемых электронов определяется частотой излучения;

•  безынерционность – одномоментное (~10^-9с) появление или исчезновение эффекта с падающим излучением.

 

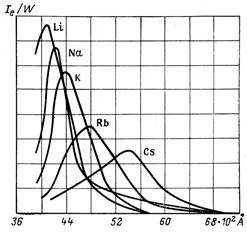
Рис.3.5

 

 Основными характеристиками фотоэмиссии являются величина квантового выхода и спектральная чувствительность. Квантовый выход определяется как отношение числа эмитированных электронов (N_e) к числу падающих на поверхность фотонов (N_ф):  ^ N^e N_ф . Величина квантового

выхода зависит от рода материала и от частоты падающего на фотокатод света. Для монохроматического излучения с длиной волны λ квантовый

I_фhc

выход определяется соотношением:  ~ .

eФ

 При однофотонном фотоэффекте, когда энергия фотона порядка работы выхода, величина  для чистых металлов не превосходит 10^-2 эл./квант. Увеличение частоты падающего электромагнитного излучения выше порогового значения приводит к резкому увеличению величины , что связано с уменьшением отражательной способности металлов при h10эВ.   Дальнейшее увеличение частоты приводит к возрастанию величины квантового выхода (рис. 3.5). При некоторой частоте на характеристике наблюдается максимум. Зависимость квантового выхода электронов от частоты света называется спектральной характеристикой фотокатода. Величина плотности фототока (однофотонная эмиссия) вблизи длинноволновой границы описывается параболическим законом Фаулера J_ф  ch²(0)² при Т= 0 К. Многофотонная эмиссия, когда в результате поглощения нескольких фотонов испускается один электрон, происходит при большой интенсивности света (Ф~ >10¹² Вт/см²). Спектральная чувствительность фотокатода определяется как коэффициент пропорциональности между величиной фототока и величиной

Iф

монохроматического       светового       потока:          ^S  ~ .         Спектральная

 Ф

чувствительность фотокатода, как и квантовый выход, зависит от материала фотокатода (типа кристалла) и частоты падающего излучения. Зависимости фототока, чувствительности катода и его квантового выхода от длины волны падающего излучения или частоты этого излучения называются спектральными характеристиками фотокатода, которые определяются материалом фотокатода.

 

 

 

 

 

 

 

Основные характеристики приемников излучения

Чувствительность. Важнейшим параметром приемников является интегральная чувствительность S, которая определяется как отношение величины электрического сигнала, выраженной в единицах напряжения или тока на выходе приемника, к величине светового потока в люменах на его входе. Однако в спектроскопии используется больше спектральная

чувствительность S_, относящаяся к монохроматическому излучению. 

Шумовые и пороговые параметры. Помимо полезного сигнала на выходе фотоприемника имеет место хаотический сигнал со случайной амплитудой и спектром – это шум фотоприемника. Шум не позволяет регистрировать сколь угодно малое значение входного излучения, так как оно становится неразличимым на фоне шума. В связи с этим вводят  пороговую чувствительность,  определяемую минимальным сигналом на его выходе, который можно заметить на фоне его собственных шумов.  Шумы в приемниках излучения имеют разную природу: 

1)              фотонный шум – шум излучения, обусловленный  флуктуацией числа фотонов, поступающих на приемник в единицу времени;

2)              дробовой шум - флуктуации темнового тока, возникающие при отсутствии освещения;

3)              тепловой шум, соответствующий обычному некогерентному излучению, которое испускается любым телом при отличной от нуля температуры;

4)              низкочастотный шум, мощность которого пропорциональна частоте, имеет место практически во всех приемниках излучения. В зависимости от типа приемника эти шумы носят разное название.   

Квантовая эффективность. Наблюдаемость сигнала определяется отношением его мощности Р к  мощности шумов Р_ш, поступающих вместе с ним. В реальных устройствах шум на выходе может оказаться меньше, чем на входе. Для характеристики приемного устройства в целом вводят квантовую эффективность равную

                      = (Р/Р_ш)_вых/(Р/Р_ш)_вх.                                                                     (7.10)

Величина  удобна для сравнения любых приемников излучения в реальных условиях. 

 Инерционность приемников. Отклик фотоприемника на поданный сигнал не может быть мгновенным. Быстрота его реакции обусловлена физическими процессами, протекающими в нем при освещении. Быстродействие фотоприемников играет важную роль при переменном сигнале. Замедленность реакции фотоприемника приводит в этом случае к падению чувствительности при превышении критической частоты модуляции сигнала. Инерционность фотоэлектронных приемников намного меньше, чем тепловых. 

Фотоэмиссионные приемники. К фотоэмиссионным приемникам относятся фотоэлементы, фотоумножители и электронно-оптические преобразователи. Фотоэмиссионные приемники отличаются более высокой чувствительностью, чем тепловые. 

Принцип работы электровакуумных фотоэлектронных приборов основан на использовании фотоэлектронной эмиссии.

 Фотоэлемент – прибор, в котором используется явление внешнего фотоэффекта. Различают электровакуумные и газонаполненные фотоэлементы. Наиболее часто используют фотоэлементы, которые имеют два электрода: фотокатод, служащий источником электронов, и анод, собирающий электроны. В видимой, инфракрасной и ближней ультрафиолетовой областях спектра чаще применяют фотокатоды на основе полупроводниковых материалов. Основными параметрами фотоэлементов являются чувствительность, квантовый выход или квантовая эффективность, шумы, минимально регистрируемая мощность излучения (пороговый поток), обнаружительная способность, темновой ток, постоянная времени и др. К основным характеристикам фотоэлементов относятся: спектральные, вольтамперные (рис. 7.13), энергетические 

(рис .7.14), частотные и температурные.

                                    

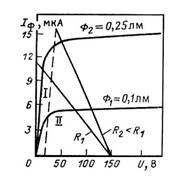
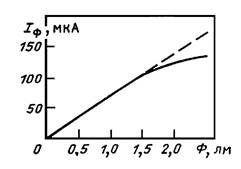
Рис. 7.13. Вольт-амперная Рис. 7.14. Энергетическая характеристика фотоэлемента      (световая) характеристика фотоэлемента.

 

Частотные характеристики определяются инерционностью фотоэлементов. Обычно электровакуумные фотоэлементы имеют частотный диапазон до 10⁶ Гц.

Спектральными характеристиками фотоэлементов называют зависимости монохроматической чувствительности S_λ  от длины волны излучения λ, воздействующего на фотокатод фотоэлемента. Эти характеристики зависят в основном от электрофизических параметров материалов, из которых изготовлены фотокатоды.  Спектральные характеристики сурьмяно-цезиевых и кислородно-цезиевых катодов показаны на рис. 7.15.

 

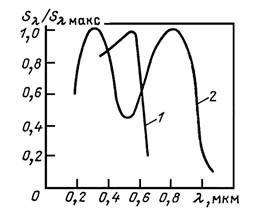
Рис. 7.14. Спектральная характеристика сурьмяноцезиевых (1) и кислородно-цезиевых (2) катодов Фотоэлектронные         умножители       (ФЭУ)         представляет       собой

электровакуумный фотоэлемент, объединенный с электронной усилительной системой в едином корпусе (баллоне). Действие усилительной системы основано на явлении вторичной электронной эмиссии. Устройство

фотоэлектронного умножителя показано на рис. 7.16, а, б.

Эмитируемые фотокатодом (ФК) электроны, ускоряемые и фокусируемые электродами, попадают на первый динод Д₁, с коэффициентом  вторичной  эмиссии σ. 

 

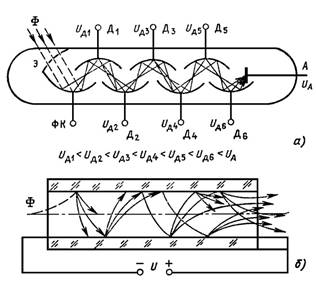
Рис. 7.16. Устройство фотоэлектронного  умножителя

Часть электронов теряется в фокусирующей и ускоряющей системе (на

сетке Э, рис. 7.16, а), что обычно учитывается с помощью коэффициента _k.    С поверхности первого динода выйдет в σ  раз большее число электронов, чем на него упадет. Появившиеся после бомбардировки первого динода вторичные электроны ускоряются полем второго динода Д2 и выбивают из него вторичные электроны, т.е. со второго динода уйдет в σ² раз большее число электронов и т. д. К аноду придет поток электронов в σ^m раз больший, чем было испущено катодом (m — число динодов). 

Ток, протекающий в цепи анода, будет равен I_A = _k MI_k, где I_k – ток эмиссии с фотокатода. Число динодов в ФЭУ может быть более 10. При коэффициенте вторичной эмиссии, равном 4, это соответствует увеличению фототока в 10⁶ раз.

Постоянная времени ФЭУ определяется временем развития электронной лавины и составляет обычно 10^-7–10^-8 сек.

Спектральная область работы ФЭУ определяется областью чувствительностью фотокатода и прозрачностью выходного окна. Недостатком ФЭУ является некоторая нестабильность и повышенный темновой ток. При охлаждении жидким азотом удается добиться пороговой чувствительности, соответствующей регистрации одного фотона в секунду.

Электронно-оптические преобразователи (ЭОП) предназначены для преобразования оптического изображения из одной области спектра в другую или для усиления яркости изображения. В простейшем случае ЭОП имеет вакуумированный корпус с окном, на которое с внутренней стороны нанесен фотокатод, преобразующий оптическое изображение объекта в электронное. Фотоэлектроны дают изображение объекта на люминесцирующем экране, который вновь преобразует электронное изображение в оптическое. Яркость изображения в одном каскаде ЭОПа повышается в несколько десятков раз, в многокаскадных ЭОПах усиление достигает 10⁴. 

 

 

 

 

 

 

 

 

 

3.3. Термоэлектронная эмиссия

Явлением   термоэлектронной       эмиссии      (ТЭ) называется испускание электронов нагретыми телами (эмиттерами). Термоэлектронная эмиссия является одним из видов эмиссии электронов поверхностью твердого тела. В случае          термоэлектронной        эмиссии      внешнее     воздействие         связано       с нагреванием твердого тела. Источником энергии возбуждения электронов является энергия теплового движения решетки твердого тела. Основным недостатком металлических катодов является высокая работа выхода, что требует высоких рабочих температур. Например, для получения ТЭ заметной величины большинство тугоплавких металлов необходимо нагревать до температуры (2000 – 2500) К. Для выхода электрона из металла необходимо, чтобы его энергия была больше потенциального барьера. Однако этого недостаточно. Необходимо также, чтобы электрон с этой энергией мог двигаться перпендикулярно поверхности металла, имея ввиду то, что с какой бы скоростью ни двигался электрон параллельно поверхности, он никогда не покинет металл. Число электронов, эмитируемых при фиксированной температуре с единицы площади поверхности в единицу времени в перпендикулярном направлении, равно N  4^k₃²mT² exp_U^pkTU^F _.       Согласно          квантово-механической h      _

теории, не все электроны выходят в вакуум. Есть вероятность отражения их от потенциального барьера. Поэтому вводится понятие прозрачности барьера

D. Тогда плотность тока определяется формулой (формула Ричардсона-

Дэшмена): JT  DA0T2 expekT  DA0T2 expkT  ,        где                                                     индекс                                    Т

                                                            

указывает на термоэлектронный характер эмиссии, а D - средний

коэффициент прозрачности потенциального барьера, A₀  ^4k23^me  ⁶ A м^2  K^2 и U_p U_F e - работа выхода.

1,210 _h

Формула Ричардсона-Дэшмана носит универсальный характер. С помощью

J^T C^ 1 ^^e^^ где C  ln A₀ .  логарифмирования получаем: ^ln 

                                                                                         T_{2                   }T_ k _,

J^T от ^^1 есть прямая линия. По пересечению этой

          Зависимость ln T _{2              T }

прямой с осью ординат вычисляют ln ^A₀ , а по углу наклона прямой определяют работу выхода (рис. 3.6). Кроме полной плотности эмиссионного тока представляет интерес угловое распределение эмиссии, описываемое

законом Ламберта: ^dj  ¹ J_T cos, где γ – угол эмиссии относительно d 

внешней нормали к поверхности катода, dΩ – элемент телесного угла. Приложенное внешнее поле формирует параллельный пучок электронов, поэтому данная закономерность не может быть обнаружена экспериментально.

 

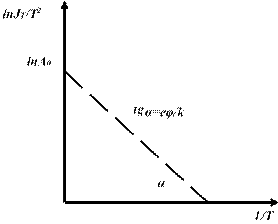
Рис. 3.6 

 

3.4. Контактная разность потенциалов

При электрическом контакте двух металлических тел с разными значениями работы выхода на границе поверхности этих тел появляется электрическое поле: возникает контактная разность потенциалов (рис. 3.7). 

r

 

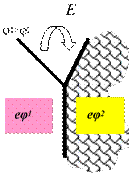
Рис.3.7 

Рассмотрим процессы, приводящие к ее возникновению. На рис. 3.8а представлены энергетические диаграммы двух незаряженных металлов с различным потенциалом работы выхода, изолированных друг от друга. В этом случае уровни вакуума у этих металлов совпадают, а уровни Ферми не совпадают. При электрическом контакте (рис. 3.8б) должно установиться равновесие. Электроны из металла с потенциалом φ₂  начнут переходить в металл с потенциалом φ1. Это приводит к тому, что проводник, теряя электроны, заряжается положительно, а другой проводник, приобретая дополнительный отрицательный заряд, заряжается отрицательно.  По мере перехода электронов уровни Ферми в металлах совпадут. Установившаяся разность потенциалов называется контактной разностью потенциалов. 

 

 

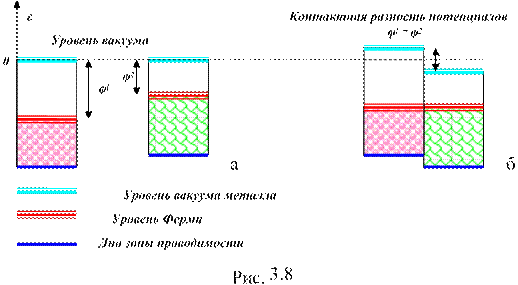
Следовательно,   контактная разность     потенциалов        определяется разностью работ выхода электронов из контактирующих проводников. Полученный результат справедлив для любых способов обмена двух материалов электронами, в том числе и путем термоэлектронной эмиссии в вакууме, через внешнюю цепь и т.д. Таким образом, возникающее электрическое поле необходимо учитывать при  работе электровакуумных приборов. 

Простейшим прибором для наблюдения эмиссии и ее сопровождающих явлений является вакуумный диод, состоящий из двух металлических электродов: эмитирующий – катод с потенциалом φ_к и собирающий – анод с потенциалом φ_А, помещенных в объем с низким давлением остаточных газов. К электродам подключен источник внешнего напряжения и между катодом и анодом образуется электрическое поле, действующее на электроны.

Типичная вольтамперная характеристика (ВАХ) вакуумного диода представлена на рис. 3.9. Если потенциалы работы выхода материалов катода и анода различны, то между электродами наряду с внешним приложенным напряжением существует контактная разность потенциалов. При наличии контактной разности потенциалов ВАХ в целом смещается по оси анодного напряжения влево или вправо в зависимости от соотношения между величинами φ_к и φ_А . Так, при φ_к < φ_А анод заряжен отрицательно относительно катода ВАХ, сдвигается на величину контактной разности потенциалов в сторону положительного потенциала. При ином соотношении между φ_к и φ_А направление сдвига ВАХ противоположно.

 

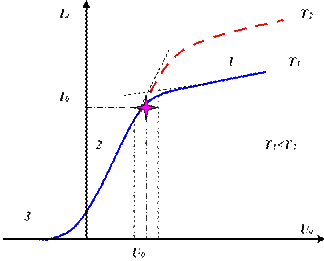
Рис. 3.9

 

Из рис. 3.9 видно, что на участке выше U0 при увеличении разности потенциалов между катодом и анодом ток не выходит на насыщение согласно соотношению Ридчарсона-Дэшмана, а непрерывно возрастает. Это явление получило название эффекта Шоттки и обусловлено снижением потенциального барьера  под воздействием приложенного внешнего

1 ³² E. С учетом тока термоэмиссии электрического поля:  e

                                                                                     40                    

плотность тока определяется выражением: JТШ  JT expkT  JT expkTe324E 

                                                                                                                   .                                                                0 

Таким образом, в результате  эффекта Шоттки ток термоэмиссионного диода при положительном напряжении на аноде растет с ростом анодного напряжения. Следует отметить, что влияние электрического поля тем больше, чем ниже рабочая температура.

                 Рабочие      температуры      большинства      металлических      катодов,

выполненных из тугоплавких металлов (вольфрам, тантал и др.), составляют (2000 – 2800)⁰С. Эмиссионная способность сильно зависит от температуры: повышение температуры вольфрама с 2400 до 2500 ⁰С приводит к росту тока эмиссии на 150% и для указанного диапазона составляет несколько сот мA/см². Недостатком металлических катодов является небольшая величина J_T при значительной потребляемой мощности и малый ресурс. Для увеличения эмиссионных характеристик используют сплавы тугоплавких и легкоплавких металлов, включая щелочно-земельные металлы. Тугоплавкая компонента композиционного катода обеспечивает высокую механическую прочность, а легкоплавкая, образующая тонкую пленку на поверхности катода, способствует увеличению эмиссионного тока благодаря уменьшению работы выхода. Снижение потенциального барьера в этом случае связано с тем, что на поверхности катода формируется поверхностный дипольный слой, электрическое поле которого противоположно полю потенциального барьера. Так для катода Th-W работа выхода составляет eφ= 2.7 эВ, а плотность тока достигает 1.5 A/см². У катодов Ba-W (eφ= 1.6 эВ) , Cs-W (eφ= 1.5 эВ) эффективность выше в связи с меньшей работой выхода.

Широкое распространение получили также оксидные катоды и катоды из тугоплавких боридов, щелочно- и редкоземельных металлов. Если первые в большинстве своем применяются в отпаянных электровакуумных приборах, то вторые могут применяться и при не столь высоких требованиях к вакуумным условиям.

Наиболее часто на практике реализуются два типа конструкций термоэмиссионных катодных узлов: катоды прямого накала (ток пропускается непосредственно через эмитирующий электрод) и катоды косвенного накала (нагреватель размещен внутри полой металлической детали, наружная поверхность которой эмитирует электроны). 

Основными характеристиками термоэмиссионных катодов являются рабочая температура - температура поверхности катода в нормальных рабочих условиях.  удельная эмиссия - величина тока электронной эмиссии с единицы поверхности катода. 

удельная мощность накала – мощность накала, приходящаяся на единицу поверхности катода. 

эффективность катода - отношение тока эмиссии к мощности накала. ресурс катода - среднее время безотказной работы. 

Основные характеристики типичных термокатодов представлены в таблице: 

Тип	Материал	Рабочая температура, 0С	Плотность тока, A/см2
Металлический	W	2000 - 2300	0.7 – 1/5
Торированный	Th-W	2000	3
Оксидный	BaO3	650-900	1
Боридный	LaB6	1500 -1700	50

 

3.5. Автоэлектронная эмиссия

Автоэлектронная эмиссия представляет собой испускание электронов из катода под влиянием сильного внешнего электрического поля со стороны вакуума. В эксперименте этот вид эмиссии происходит в электрических полях с напряженностью Е ≥ 10⁶ В/см. Суть процесса в том, что при действии сильного внешнего электрического поля на границе металл-вакуум изменяется форма потенциального барьера (рис.3.10). В этом случае потенциальный барьер имеет конечную ширину. Согласно квантовой механике для электронов, находящихся в такой потенциальной яме, становится возможным туннельное прохождение сквозь потенциальный барьер. Чем уже и ниже потенциальный барьер, тем больше вероятность туннелирования электронов. Электроны, имеющие разную энергию ε, имеют и разную вероятность выхода из металла. Наибольшую вероятность выхода имеют электроны с энергией, близкой к энергии Ферми. Высота и ширина барьера существенно зависят от напряженности приложенного электрического поля Е: чем больше напряженность поля, тем ниже и уже барьер и тем больше эмиссионный выход электронов. 

 

 

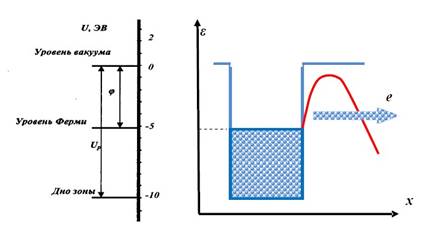
Рис. 3.10

 

Плотность тока при автоэлектронной эмиссии  может быть определена при помощи упрощенного выражения закона Фаулера-Нордгейма:  

J_А  AE^21 ₂₄5_EE₀^_exp^_ 4₃E_E⁰_^,       где    А       –        константа, определяемая _

свойствами границы раздела и структурой металла, величина ^E₀  ^ 2m , eh

которая для металлов имеет порядок 10⁹В/см. Согласно формулам плотность тока автоэмиссии резко зависит от напряженности электрического поля. Поэтому в экспериментах увеличения напряженности поля добиваются применением катодов, имеющих остроугольную геометрию, на остриях которых достигается максимальная напряженность электрического поля. Для получения еще больших токов необходимо иметь еще и достаточно большую эмиссионную поверхность. Поэтому катод делают либо многоострийным с радиусом закругления 10^-4— 10^-5 см, либо плоским, поскольку даже на полированной плоской металлической поверхности имеются острия микроскопических размеров. 

                                        

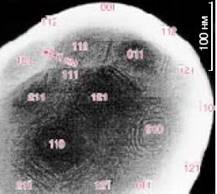
                                                 а                                                            б

Рис. 3.11

 

В области сильноточной электроники (10⁶А/см²), чтобы обеспечить большой ток эмиссии, необходимо применение катодов с большой плотностью тока. При более высоких плотностях тока (10⁸А/см²) происходит омический разогрев отдельных участков. Пондеромоторные силы, действующие на материал катода, приводят к взрывообразному разрушению отдельных участков катода. Из продуктов эрозии катода образуется прикатодная плазма. Это явление взрывной электронной эмиссии, эффективно используемое в физике сильноточных релятивистских электронных пучков (СРЭП). 

Автоэлектронная эмиссия может наблюдаться и при напряжениях сотен вольт при малых радиусах кривизны 20-50 Ǻ. Использование явления автоэлектронной эмиссии позволили создать современные фундаментальные методы исследования топологии поверхности с атомным разрешением – электронная микроскопия, туннельная микроскопия и др. В качестве примеров на рис. 3.11а представлена фотография острия-монокристалла W полученная с высоким разрешением (8Ǻ) в растровом микроскопе S900 (Hitachi), а на рис. 3.11б - многоострийная матрица с сотовым анодом современного плоского дисплея (радиус острия (20 -30 Ǻ), расстояние анод катод 1-2 мкм). 

 

3.6. Вторичная электронная эмиссия

Явление эмиссии электронов при бомбардировке поверхности вещества потоком электронов получило название вторичной электронной эмиссии. Причина этого эффекта заключается в том, что первичные электроны, взаимодействуя с электронами твердого тела, передают им часть своей энергии. Если эта энергия достаточна для преодоления электронами твердого тела поверхностного потенциального барьера, то они покидают его и регистрируются как вторичные электроны. Вторичные электроны обладают энергиями от нуля до энергии первичных электронов. Энергетическое распределение вторичных электронов имеет сложный характер и отражает разнообразные и часто связанные между собой процессы взаимодействия первичных электронов с твердым телом.

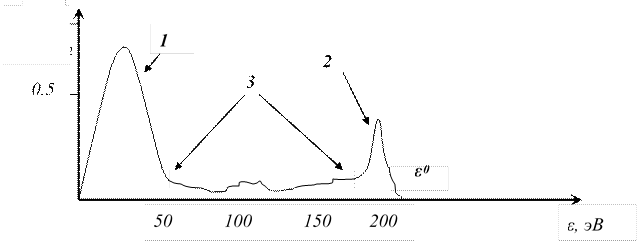1   δ

                           Рис. 2.17 – ^{Распределение вторичных электронов по энергиям}Рис. 3.12  

На рис. 3.12 представлена функция распределения электронов, испущенных поверхностью металла при его бомбардировке первичными электронами с энергией 200 эВ. Видно, что вторичные электроны разбиты на три группы: истинно вторичные электроны (1), упруго отраженные поверхностью первичные электроны (2) и группа неупруго рассеянных первичных электронов (3). Максимум распределения электронов в группе 1 приходится на энергию ~10 эВ, причем основная масса этих электронов сосредоточена в энергетическом интервале 5 – 20 эВ. Экспериментально было показано, что эта закономерность практически не зависит от энергии первичных электронов. Отношение тока (количества) истинно вторичных электронов к току (количеству) первичных называется коэффициентом вторичной эмиссии – δ. Механизм возникновения истинной вторичной эмиссии состоит в том, что первичные электроны с энергией ε0, проникая в металл, тормозятся вследствие кулоновского взаимодействия с электронами проводимости. Потери первичных электронов описываются законом Виддингтона:

1

²

_x ₀ ^x², где ε_x – энергия первичных электронов, прошедших путь x в

материале мишени, α – постоянная Виддингтона, значения которой лежат в диапазоне (10¹⁰ - 10¹²)эВ²/см. Ввиду того, что энергия первичных электронов

существенно превышает энергию ионизации и возбуждения атомов ε_а (сечения взаимодействия малы), первичный электрон в начале пути теряет энергию, не создавая вторичных электронов.

На некоторой глубине энергия первичных электронов снизится до оптимальной, при этом вероятность ионизации резко возрастет. При каждом взаимодействии возникают возбужденные электроны (вторичные), а скорость первичных резко изменяется по величине и направлению. Часть этих электронов движется из глубины металла, взаимодействуя с электронами проводимости, узлами кристаллической решетки и их количество уменьшается по экспоненциальному закону. С ростом энергии первичных электронов, увеличивается число электронов, обладающих энергией, достаточной для эмиссии. Вместе с тем образование вторичных электронов происходит в глубине материала и этим затрудняет их выход. Совместное действие этих факторов приводит к тому, что существует оптимальная энергия первичных электронов, при которой коэффициент δ имеет максимальное значение. На рис. 3.13 представлена зависимость выхода вторичных электронов от энергии бомбардирующих электронов.

Основной характеристикой эмиссионных свойств вещества является зависимость коэффициента вторичной электронной эмиссии δ от энергии первичных электронов ε. Для большинства веществ максимальное значение коэффициента δ больше единицы. Характерная зависимость δ(ε) имеет практически одинаковый вид для большинства веществ (металлов, диэлектриков и полупроводников, рис. 3.13). 

 

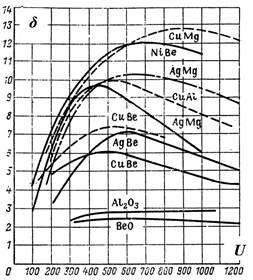
Рис.3.13

Для чистых металлов 0,5 < δ_макс< 1,8, что соответствует энергии первичных электронов от 0,2 до 0,9 кэВ (рис. 3.14а). Малые значения коэффициента δ в металлах связаны со значительными потерями энергии вторичных электронов.

 

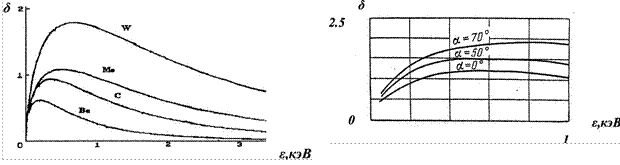
                                                   а                                                              б

Рис. 3.14

Электроны, образовавшиеся на большой глубине, при подходе к границе вещество-вакуум обладают энергией, недостаточной для преодоления потенциального барьера. Однако вторичные электроны (истинно вторичные электроны), возникшие в приповерхностном слое, обладают достаточно большой энергией и, преодолевая потенциальный барьер, покидают металл. Кроме того, коэффициент вторичной эмиссии зависит от угла падения первичных электронов α (рис. 3.14б) согласно формуле: e_^e0cos_, где β= 1.3 – 1.5.

Детальное изучение энергетических спектров и угловых распределений вторичных электронов позволяет получить достаточно полную информацию об основных микроскопических характеристиках поверхности: составе, структуре, электронном строении.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ИНТЕНСИВНЫЕ ЭЛЕКТРОННЫЕ ПУЧКИ

 

4.1. Вакуумный диод

Физические свойства пучков заряженных частиц широко используются в целом ряде разделов вакуумной электроники и представляют интерес для многих областей науки и техники. Создание направленных, управляемых пучков (потоков) заряженных частиц осуществляется при помощи разнообразных устройств, непременным атрибутом которых является источник заряженных частиц. Достаточно распространенным элементом такой системы, обеспечивающим получение интенсивного, хорошо сфокусированного пучка электронов является электронная пушка. Наиболее часто применяются термоэлектронные пушки, в которых первичным элементом является вакуумный диод. 

Рассмотрим наиболее типичные процессы, влияющие на формирование тока в вакуумном диоде. Для простоты рассмотрим диод, образованный бесконечно протяженными плоскими электродами, один из которых является термоэмиссионным катодом. При отсутствии напряжения между катодом и анодом (внешняя цепь разорвана) эмитированные с катода при температуре Т_е электроны заполняют объемным зарядом межэлектродное пространство и движутся к аноду с тепловыми скоростями. В таких условиях, когда потенциал анода достигнет величины ^kTe , установится динамическое e

равновесие, при котором скорости эмиссии и поглощения электронов катодом будут равны. Распределение потенциала в межэлектродном пространстве при равновесии изображено на рис. 4.1(1). Подключение внешней цепи и подача напряжения на анод приводит к появлению тока в анодной цепи. В этих условиях даже малые значения потенциала на аноде kT^e приводят к изменению распределения потенциала в a 

e межэлектродном пространстве. Плавное увеличение анодного напряжения приводит к увеличению анодного тока. В этом случае происходят плавные изменения межэлектродного распределения потенциала. Положение минимума потенциала в межэлектродном пространстве при увеличении потенциала анода, как видно из представленных на рис. 4.1 зависимостей, смещается к аноду с одновременным уменьшением его абсолютной величины.

                                                                 

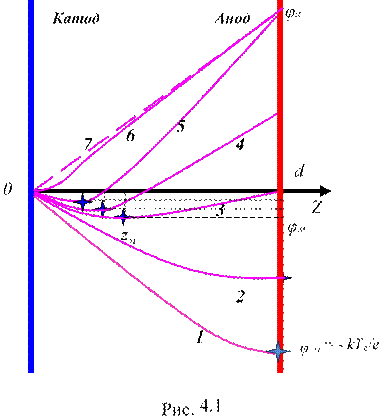
Рассмотрим ВАХ диода (рис. 4.2), соответствующую различным зависимостям распределения межэлектродного потенциала. Как видно из рисунка, ВАХ диода имеет различные характерные участки: область 3 соответствует таким значениям анодного тока, при которых минимум потенциала приходится на анод; область 2 – в межэлектродном пространстве формируется потенциальная яма («виртуальный катод»), который смещается к катоду при повышении анодного напряжения; область 1 – область d

насыщения, в которой 0 во всем межэлектродном промежутке.

dz

 

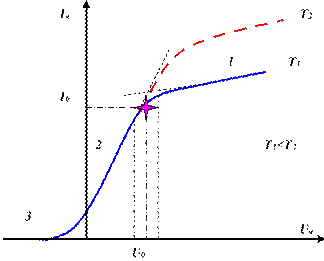
Рис. 4.2

 

Такая зависимость при постоянном значении тока эмиссии (Т_к - const) объясняется увеличением числа электронов, достигающих анода при увеличении напряженности поля. 

Если считать, что начальные скорости электронов, эмитированных с катода, равны нулю, т.е. энергия теплового движения электронов гораздо меньше энергии, приобретаемой ими в межэлектродном промежутке, то в ВАХ будет отсутствовать область 3, так как наличие потенциальной ямы (отрицательного поля) у поверхности катода не позволило бы ни одному электрону достичь анода. Таким образом, в зоне пространственного заряда, на кривой распределения потенциала (рис. 4.1), не будет наблюдаться минимум. Плавное возрастание тока анода с увеличением анодного напряжения свидетельствует о том, что поле у поверхности катода имеет нулевое значение независимо от величины пропускаемого тока, так как при Е>0 во всем промежутке, ток достигал бы значения насыщения скачком.

В случае движения заряженных частиц в вакууме, когда влиянием пространственного заряда можно пренебречь (объемный заряд мал) z

распределение потенциала в межэлектродном пространстве Uz^U_a               d

(рис. 4.2, кривая 7) представляет собой решение уравнения Лапласа. Однако в большинстве приборов используются значительные токи и формируются объемные заряды такой плотности, что ими нельзя пренебрегать. Оказывается, что плотность тока в диоде не может превышать некоторого предельного значения. Причина ограничения плотности тока связана с действием пространственного заряда электронов, находящихся в диоде. При достаточно большой плотности тока поле у катода сравнивается с направленным противоположно внешним полем и эмиссия электронов из катода прекращается. Для определения зависимости тока от анодного напряжения и распределения потенциала в межэлектродном пространстве системы плоских электродов без учета тепловых скоростей необходимо воспользоваться уравнением Пуассона. В предположении плоского диода, когда расстояние между электродами d значительно меньше их линейных размеров, можно приближенно считать, что параметры потока зависят лишь от одной переменной z (расстояние от катода). В стационарном режиме сохраняется плотность тока: j const , так как в любой точке z заряд не накапливается и не исчезает. Скорость электрона в межэлектродном

1

пространстве равна 2eUz 2. Очевидно, что вблизи катода _v

                                                                            m    

минимальна, а  ρ- максимальна. C учетом граничных условий и указанных выше предположений решение уравнения Пуассона (в режиме ограничения тока пространственным зарядом) позволяет получить связь между текущим через диод током I  jS (S – площадь поверхности электродов) и

1 2e S 3²  ^PU_a3² Это формула Чайлда-Ленгмюра напряжением:^I_s  9 d₂^U_a

                                                        _ m                            .

(закон степени 3/2). Коэффициент P, равный для тока электронов

P  2.33510^{6 S d}₂ , где Р _{выражено в} ^_В^A₃2 ^, называется первеансом диода. Потенциал в межэлектродном пространстве диода распределен по закону:

4

UzUa^ z^ ³,        а        пространственный        заряд          описывается законом d

Ленгмюра-Богуславского: z Ua₄ z23 .

9d ³

С учетом теплового разброса скоростей эмитируемых электронов закон

Чайлда-Ленгмюра          для          плоской          системы          имеет          вид:

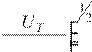ja  2.33106 da zм2 1 2.66a м         , UT  kTek 11600Tk     В,       

где Т_к – температура катода. Значение φ_м определяется из уравнения:

j^e j_e - плотность тока эмиссии катода при рабочей _м  ^U_T ln , где

j_a

температуре. Положение минимума потенциала (виртуального катода)

3

^{T 4}

определяется из выражения: ^z_м 2.7310^{6 k}            см, здесь j(А/см²⁾. 

₁ j_a2

4.2. Движение потоков заряженных частиц

В ряде современных электронных приборов используются направленные управляемые потоки (пучки) электронов, создаваемые с помощью магнитных и электрических полей. Под пучком заряженных частиц обычно понимают поток частиц, движущихся в одном направлении примерно параллельно друг другу: разброс по энергиям и отношение поперечной скорости к продольной составляют не более нескольких процентов. Обычно рассматривают распространение пучка в вакууме 

(10^-5 – 10^-3 Па). Объемный заряд пучка может оказаться сильнейшим фактором, влияющим на свойства пучка. В пучке частиц одного вида могут присутствовать и другие частицы, взаимодействующие с ним. Если взаимодействие становится столь значительным, что частицы пучка приобретают поперечную скорость, то утрачивается основной признак пучка.

Особенно быстро это проявляется в среде с повышенным давлением, хотя ограниченное расстояние пучок может проходить и в плотных средах.

Во всех случаях движение заряженных частиц происходит под действием электрических и магнитных полей. Следовательно, полное описание поведения пучка может быть получено из уравнений движения и известного распределения полей.

Широко распространенными типами электрических и магнитных полей, используемых в технике пучков, являются аксиально-симметричные поля, анализ движения в которых проводят в цилиндрических координатах (r,,z). В таких полях отсутствуют азимутальные компоненты: ^E_ ^B_ 0.

r

Вводя магнитный поток   _ ^B_z 2rdr, из уравнений движения можно

0

получить соотношение r²^&   e        const, известное как теорема Буша. 2m

Она     связывает    угловую    скорость    частицы    с    магнитным     потоком,

пронизывающим ее траекторию (рис. 4.3а).

Движение в аксиальном и радиальном направлениях приводит к изменению магнитного потока, пронизывающего траекторию частицы (рис. 4.3б). Если в качестве начальной точки траектории взята точка, лежащая на катоде, то _н имеет смысл магнитного потока _к , сцепленного с круговым контуром радиуса r_k.

                                                     а                                                            б

Рис. 4.3

 

При ^& _к 0 из теоремы Буша следует, что ^&  2 e          (^{ }₂^н)^. Используя

                                                                                                                                             _m       r        

это соотношение, можно получить модифицированные уравнения движения. Анализ уравнений приводит к следующим выводам: радиальная сила, действующая на частицу со стороны магнитного поля, определяется не только величиной индукции, но зависит от разности магнитных потоков _к , причем эта сила стремится к нулю когда _к 0. Изменяющееся вдоль оси z магнитное поле (^  0) создает z-компоненту магнитной силы, z

которая приводит к торможению или ускорению частиц в этом направлении.

Для параксиального пучка приложенные силы (потенциалы и магнитные потоки) можно представить в виде разложения первого порядка по степеням малого радиального отклонения от оси:  r^2B_z0^{, B}_z  ^B_z0,

B_r   r B_z₀, ^U  _ ^rU₀_^{, U} _ ^U0  U₀ . С учетом этих соотношений можно

                 2            r        2           z       z

получить уравнения, описывающие движение приосевых частиц.

Рассматривая в качестве независимой переменной координату z можно получить уравнение траекторий частиц: 

ddz2r  U0 dr  U0 r  e r Bz20 1 rrк22BBzz00к 2  0.

                                                                  2 2U0 dz 4U0                         8m U0      

 

4.3. Особенности движения потоков заряженных частиц

                Помимо    сил    внешнего    электромагнитного    поля    на     частицы,

движущиеся в пучке, действуют силы собственных электрических и

                                                                     r      r

магнитных полей пучка ^F_e и ^F_B (рис. 4.4). Радиальное электрическое поле (и

r сила ^F_e) обусловлено объемным зарядом пучка, а азимутальное магнитное

r

поле (и сила ^F_B) вызывается током пучка. Начиная с некоторой плотности частиц в пучке, эти силы могут оказать существенное влияние на движение

r

частиц. Расталкивающая кулоновская сила ^F_e приводит к увеличению

r

поперечного сечения пучка, а сила магнитного стягивания ^F_B  действует в

противоположном направлении. Рассмотрим пучок электронов цилиндрической формы с радиусом а и равномерной плотностью п. Пучок создает электрическое поле с напряженностью Е_е  2епа и магнитное 

 

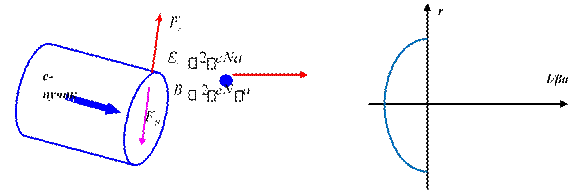
Рис. 4.4

 

поле с индукцией В  2епа, где  v/c. Результирующая сила, действующая на частицу со стороны собственных полей пучка, равна: F_e F_B  eE_e eB 2e²na1² F_e^2. Отсюда следует, что в нерелятивистском приближении влиянием собственного магнитного поля можно пренебречь. В случае релятивистских пучков радиальное электрическое поле объемного заряда компенсируется силой Лоренца релятивистских электронов.

Собственный объемный заряд оказывает существенное влияние на движение пучка и в продольном направлении. При ускорении электронов во внешнем электрическом поле собственный заряд ослабляет ускоряющее поле вблизи катода и накладывает ограничения на ток пучка. Это ограничение для тока между катодом и анодом, представляющих собой две бесконечные плоскости, определяется законом Чайлда-Ленгмюра. 

Потенциал пучка зависит от плотности объемного заряда. При одинаковом токе и энергии частиц разность между потенциалами в центре и на краю пучка определяется также его размерами и геометрией (рис. 4.4). Эта разность существенно меньше в ленточном и трубчатом пучках, поэтому в ленточном и трубчатом пучках может быть пропущен больший ток, чем в цилиндрическом.

Существенное влияние на движение частиц может оказать ионная компенсация объемного заряда пучка. При ионизации электронами пучка остаточного газа образуются положительные ионы и медленные электроны. Вследствие более быстрого ухода из пучка медленных электронов пучок может быть частично или полностью скомпенсирован ионами, что приводит к уменьшению силы электростатического расталкивания. Время компенсации τ заряда пучка в среде давлением p примерно определяется соотношением   0.04 p^1, где τ выражено в мкс, а давление в Па. Так, в техническом вакууме ( p 10^3 10^4 Па) через 10-100 мкс после появления пучка плотность ионов в области пучка по порядку становится равной плотности электронов.

Распределение электронов по сечению пучка зависит как от характеристик инжектора, так и условий транспортировки. Наиболее типичное распределение по сечению – гауссово. В некоторых случаях пучок имеет трубчатую структуру или разбивается на отдельные струи. Как правило, у потока электронов отсутствуют резко очерченные границы. При необходимости срезать наружные слои потока, содержащие, как правило, малую часть тока, применяют диафрагмы с отверстиями, проходя через которые, пучок обретает более четкий контур. Однако при дальнейшей транспортировке границы пучка снова размываются из-за электронов, рассеянных на краях диафрагмы, взаимодействия со средой и других эффектов.

Помимо указанных способов и параметров для описания качества формируемого пучка, степени упорядоченности его структуры и

распределения поперечных скоростей используют такие понятия, как фазовая характеристика пучка, фазовый эллипс и эмиттанс пучка, яркость.

Каждый электрон пучка в заданный момент характеризуется в декартовой системе координатами x, y, z и проекциями импульса на каждую из осей p_x, ^p_y, ^p_z . Объем, занимаемый совокупностью электронов в шестимерном фазовом пространстве, называется объемом пучка, являющимся, согласно теореме Лиувилля, инвариантом вдоль траектории частиц. Фазовая характеристика пучка представляет собой множество точек в поперечном

dr ^r , где  r и r - радиальная координата и пространстве  r и r  _

dz _z

наклон каждой из совокупности траекторий, образующих электронный пучок. 

                   

 

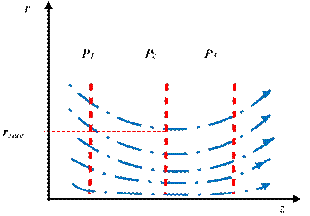
                                                 а                                                            б

Рис. 4.5 

На рис. 4.5 приведены фазовые характеристики электронного пучка: а) –ход электронных траекторий в идеально сформированном электронном пучка: пучок равномерно сжимается, достигает min сечение в плоскости Р2 и в дальнейшем под действием кулоновских сил расширяется; б) –фазовые характеристики этого пучка для плоскостей  Р₁, Р₂, Р₃. Характеристика Р1 соответствует равномерно сходящемуся в плоскости Р1 пучку, наклон dr ^r пропорционален их радиальной координате. В траекторий r  

dz _z

плоскости минимального сечения Р2 траектории пучка параллельны z, следовательно, r  0 и фазовая характеристика Р2  расположена на оси фазового пространства. Фазовая характеристика Р3 соответствует равномерно расходящемуся пучку. 

Особенностью рассмотренных характеристик является их линейность, что соответствует идеально сформированному электронному пучку. Аберрация электронной пушки приводит к нелинейности фазовых характеристик. Пример нелинейной фазовой характеристики в плоскости минимального сечения пучка приведен на рис. 4.6а. 

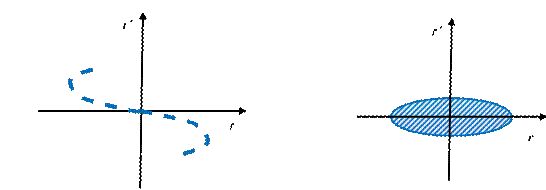
                                                 a                                                            б

Рис.4.6

 

Такая характеристика отражает эффект пересечения электронных траекторий, так как одному и тому же значению радиальной координаты соответствуют различные углы наклона траекторий. Учет теплового разброса скоростей электронов в пучке приводит к тому, что на фазовой плоскости электронный пучок отображается не линией, а некоторой фигурой, имеющей конечную площадь. В плоскости минимального сечения пучка эта фигура имеет вид прямого эллипса (рис. 4.6б). Каждой радиальной координате пучка соответствует множество значений r. Площадь фазового эллипса - А,

A

деленная на π, называется эмиттансом пучка:  Эмиттанс пучка () –

 .

площадь проекции фазового объема на плоскость смещение-наклон ( R,R ) является количественной характеристикой, позволяющей определить угловую расходимость пучка, способность фокусироваться внешним магнитным полем и т.д. Эмиттанс, связанный с тепловым разбросом скоростей, может быть определен с помощью выражения для плотности тока

в	минимальном                 сечении	пучка               (кроссовере):
j  jк	eUa2exp eUa2 r2  . kTк  kTк rк2	Это      выражение      связывает

плотность тока в пучке j с плотностью тока на катоде ^j_к , углом сходимости пучка ², ускоряющим напряжением ^U_a , радиусом ^r_к² и температурой катода. Плотность тока, достигающая значения максимума на оси системы (r=0), получила название - ленгмюровский предел плотности

eU^{a 2}             распределение плотности тока: ^j_макс  ^j_{к    } . Ввиду того, что    kT_к      

пучка подчиняется закону Гаусса на определенном радиусе, плотность тока уменьшается в «е» раз по отношению к значению на оси. Значение этого

r^к kT^к . Фазовая фигура пучка в радиуса составит: ^r_beam  2

                                                                                  eU_a

плоскости кроссовера – эллипс с полуосями (α, ^r_beam). Используя определения эмиттанса, получим его значение для пучка с тепловым

kTк где Cbeam    коэффициент разбросом: beam Cbeamrк eU_a ,

j ,. относительной доли пучка

j

Примерное значение эмиттанса - произведение диаметра пучка на его угловой раствор. Таким образом, в случае параксиальности траекторий и отсутствии ускорения, эмиттанс не меняется вдоль канала транспортировки.

При транспортировке пучка в дрейфовом канале в отсутствие продольных сил первоначально поток частиц является сходящимся, а затем его сечение возрастает. Радиус кроссовера может быть оценен исходя из соотношения ^r_beam  ^r₀^exp tg0^2_, где r₀ и α₀ - начальные радиальное положение и угол наклона, соответственно, в плоскости входа в эквипотенциальное пространство. Видно, что величина кроссовера зависит от начального угла наклона, и чем он больше, тем меньше радиус кроссовера. Существует оптимальный начальный угол схождения пучка – α_опт, отклонение от которого в ту или иную сторону приводит к смещению положения кроссовера в сторону плоскости инжекции. При данном угле длина пролетного промежутка будет максимальной. Оценить эту длину можно, если выполняется условие: tg_опт 162 ^P , где Р – первеанс,

измеряемый в АВ-3/2. Тогда zмакс  r0 tgопт .

Таким образом, в токовых каналах силы объемного заряда налагают ограничения на длину канала транспортировки интенсивных пучков вследствие быстрого возрастания их поперечного сечения. 

 

4.4. Предельный ток пучка в вакууме в эквипотенциальном транспортном канале

Рассмотрим расчет движения приосевого моноэнергетического пучка заряженных частиц круглого сечения в эквипотенциальном пространстве, ограниченном цилиндрической поверхностью с металлическими стенками представляющий практический интерес. Пусть электроны ускорены некоторой разностью потенциалов 0^. Увеличение силы тока пучка приводит к увеличению его пространственного заряда и соответствующему падению потенциала относительно стенок. Учет объемного заряда позволяет

                                                                                                                                    m             2I

найти выражение для радиального поля ^E_r  2_ 2e_0 _     r_  . Величину

_

уменьшения потенциала (“провисание потенциала”) между осью пучка (r=0)

и       его       границей       можно       определить       следующим       образом:

 

                    ^R                                 2I      R

 a Erdr  _ ln _a , где а - радиус пучка, R - радиус металлического цилиндра. Уменьшение потенциала приводит к тому, что при его значении, равном в энергетических единицах энергии электронов, что достигается при определенном значении тока, пучок запрется собственным

пространственным зарядом. Ситуация схожа с законом Чайлда-Ленгмюра для вакуумного диода, ограничивающего величину тока. 

Однако в случае вакуумного диода распределение электронов по энергиям имеет размытый характер, и часть быстрых электронов преодолевает потенциальный барьер и достигают анода. В случае пучка с малым энергетическим разбросом отсечка (ограничение) тока наступает скачком. Возникающая разность потенциалов оказывает тормозящее действие на электроны, вследствие чего скорость электронов уменьшается:

1

           2e                2

 _m ^0 ^_ . Из полученных ранее соотношений несложно получить

_ зависимость тока пучка, транспортируемого через эквипотенциальный канал,

1

2e  2

от величины провисания потенциала: I  ^mR 0 ^12 . Ток

                                                                                                                                  2ln    _a

1

2e^m 2 ^₀₃² при

достигает своего максимального значения: ^I_макс ^ 3 3lnRa       

2

макс  0.  3

Незначительное увеличение тока в пучке свыше ^I_макс в транспортном канале приводит к образованию виртуального катода, т.е. встречной тормозящей разности потенциалов, изменяющейся скачком от _{макс } ²₀ до 

                                                                                                                                                                                               3    

₀, в результате чего ток уменьшится.

 

Возникающая таким образом неустойчивость, получила название неустойчивости В.Р. Бурсиана (рис. 4.7а). Иллюстрация развития событий (рис. 4.7б): электронный пучок задерживается потенциалом сетки, незначительная часть пучка проникает в засеточное пространство. В условиях, когда R>>a, точное значение предельного тока 

может            быть           определено           исходя           из            выражения:

Рис.4.7

Объемный заряд пучка, как было показано ранее, сильнейшим образом влияет на профиль пучка и процесс его транспортировки. Однако плотность объемного заряда пучка может быть уменьшена путем ввода в пучок медленных частиц противоположного знака, создаваемых путем ионизации. В результате столкновений электронов пучка с молекулами остаточного газа образуются положительные ионы. Их накопление в области, занятой электронным пучком, может привести к частичной или полной компенсации объемного электронного заряда, что в свою очередь может существенно влиять на ход электронных траекторий, изменять геометрию пучка. Скорость образования ионов зависит от состава остаточных газов, их парциального давления, плотности заряда в электронном пучке и его скорости. Она может быть выражена формулой: n_i  B_i p( j/e)  B_i pn_ev, где n_i - количество ионов, образуемых в 1см³ в 1с; B_i - удельная ионизация, которая определяется числом ионов, создаваемых одним электроном на отрезке пути 1см, при давлении остаточного газа 133,3 Па; p_a - давление остаточного газа; j - плотность электронного тока; v - скорость электронов; n_e - концентрация электронов. Входящая в эту формулу удельная ионизация зависит от рода остаточного газа и скорости (энергии) электронов. Так для азота B_i =10 при энергии электронов 100eV; при 10³eV и 2 при 2*10³eV. Полагая, к примеру, что U ~10³B, p 1,3310^5Па, B_i  ⁴_. находим: n_i 750n_e. Отсюда

следует, что даже малой части (примерно 0,001) ионного заряда, образуемого в течение 1с, достаточно, чтобы нейтрализовать заряд электронного пучка,

т.е. необходим учет ионизационных потерь.

Эффективное сечение _i ионизации простых атомов достаточно хорошо определяется путем расчетов в борновском приближении.

Результаты этих вычислений в упрощенной форме даются соотношением:

_i ^e₂⁴ bf (U)  f (U)см²     f (U)  ^2,7 lnU;      где     U _ ^;    ε     –энергия

                I                   0                        ,                _{U                                  I}

ионизирующего электрона, I - потенциал ионизации в эргах, константа b для простых атомов примерно равна 0,2.

Как было показано выше, при транспортировке электронного пучка через длинный эквипотенциальный канал под действием объемного заряда формируется потенциальная яма, расположенная на оси симметрии. По сути, эта яма служит ловушкой для ионов, образующихся в области, занятой пучком. Накопление ионов будет нейтрализовать объемный заряд пучка, влияющий на движение электронного пучка, и величину тока в транспортном канале. В частности, в условиях ионной компенсации и при отсутствии внешних полей существенное влияние на движение электронов может оказывать собственное магнитное поле пучка, которое может приводить к сжатию пучка. На рис. 4.8 показан эффект газовой фокусировки пучка.

 

Рис. 4.8.

Таким образом, нейтрализация объемного заряда пучка зарядом положительных ионов в транспортном канале должно радикально изменить ситуацию и решить задачу пропускания токов значительной величины. Данная задача была рассмотрена Пирсом, который показал, что величина предельного тока превышает предельное значение тока Бурсиана в несколько раз ^I_Пирс  ^I_Бурс^_макс  0^ (рис. 4.9). Ввиду того, что статического провисания потенциала нет ^_макс 0 , ток Пирса превысит ток

 

Бурсиана в                               3  5.2раза. 

                                    Бурс           0 макс 

                                                                                               z                 b

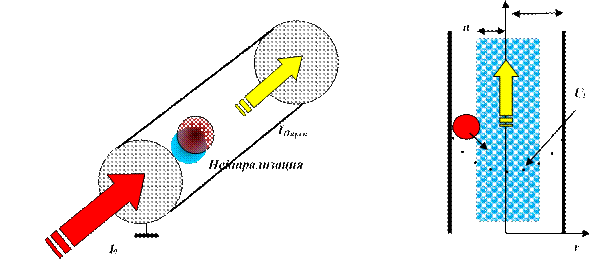
Рис. 4.9

 

 

 

 

4.5. Рассеяние электронных пучков на атомах остаточного газа

Как было показано ранее, в диапазоне давлений 10³Па и выше потери частиц в результате рассеяния на атомах остаточного газа становятся заметными и их необходимо учитывать при рассмотрении процесса ускорения. В этих условиях становится существенным эффект изменения направления движения электронов пучка при их взаимодействии с атомами. При последовательных многократных упругих взаимодействиях этот эффект приводит к рассеянию (расширению) электронного пучка. 

Рассмотрим закономерности рассеяния при однократном упругом взаимодействии. Под упругим взаимодействием понимается взаимодействие без изменения энергии электрона. В этом случае взаимодействие сводится к отклонению траектории электрона, что отражается, в конечном счете, на одном из основных параметров ускорения – интенсивности. В кулоновском поле неподвижного положительного заряженного атомного ядра угол отклонения траектории электрона описывается формулой:

e( eZ )

tg^               ₂  e²Z₂         где     θ    -    угол,    характеризующий     изменение

             2      mv b       mv b

направления траектории, eZ -  заряд ядра, e - абсолютное значение заряда электрона, Z - атомный номер, v - скорость электрона, b - прицельный параметр. Рассмотрим процесс рассеяния электронов пучка на тонком слое газа. Толщину слоя Δz будем считать достаточно малой, так что электроны испытывают однократные столкновения. Количество атомов, приходящихся на площадь, равную площади поперечного сечения пучка - S, определяется формулой: ⁿ_s  nSz , где n – концентрация атомов. Траектории электронов, проходящие этот слой, будут испытывать отклонения на различные углы θ_i, которые зависят от прицельных параметров относительно рассеивающих центров. Диапазон углов рассеяния определяется из соотношений: 

tgмин  e22Z , ra  7.4109Z13

2       m r_a

tgмакс  e²2Zrя , rя  R0A¹³,R₀ 1.510^13см,  А - массовое число ядра.

             2       m

Если ток пучка – I, то через слой в единицу времени будет проходить

N   электронов. Формула Резерфорда определяет относительное число

dN

частиц,    рассеянных    в    телесный      угол d:             ⁿ₁()d,    где

N

                    1 e²Z ²          1

()  4_{     2} _ sin_42 - дифференциальное сечение рассеяния. Известны

mv _

простые     аналитические     выражения     для     определения	полного       и
транспортного сечения с погрешностью менее 30% для 10KeV Z 1MeV : lnполн  A Bln Ek   lnтр  С  Вln Ek A 46,7375 0,7913lnZ ; B  1,2753 0,0898lnZ ; C 51,7693 1,4322lnZ ; D  1,7665 0,0386 lnZ .	8Z 54 и

При многократном упругом взаимодействии возможный ход электронной траектории показан на рис. 4.10.

                             r

 

 

 

 

 

Рис. 4.10

В точках A, B, C, D траектории происходят столкновения электрона с атомами и изменение направления его движения на углы θ_i . В качестве меры отклонения движения электрона от первоначального направления,

                                                                                                                                                                   ²            1 k              ²

используется средний квадрат углов отклонения:   ^{ }_i                                                             При

                                                                                                                                                                            k i1                .

распространение электронных пучков в атмосфере газа при повышенных давлениях, рекомендуется следующая формула для оценочных расчетов

² 8r₀²nZ^2 ₄1 ₂ ^z^lnmax , где                ^r₀ - классический радиус электрона

  min

(2,8310^15м), n - плотность газа (м-³), _max ,_min - максимальный и минимальный углы рассеяния.

Электронный пучок, инжектируемый в газ в плоскости Z=0 с малым радиусом (r0), в результате многократного рассеяния приобретает конечные размеры и характеризуется гауссовым распределением плотности тока: j(r,z)  j(0,z)exp (r r)² ln 2, где j(0, z) - плотность тока на оси, r - радиус пучка, измеренный на уровне половинной плотности тока. Величина

r выражается через средний квадрат углов рассеяния ² и пройденное

1

расстояние: r (13)(ln2)z²² ²_.

 

4.6. Электронно - оптические системы

Помимо формирования и коллимации пучка, которая осуществляется ускоряющей системой первичного диодного промежутка (электронной пушки), достаточно часто применяются системы поддержания профиля пучка вдоль канала его транспортировки (электронно-оптические системы): электростатические и магнитостатические фокусирующие  линзы. Электронно-оптическая система представляет собой совокупность электродов различной геометрии с определенными потенциалами, и магнитных систем (постоянных магнитов, соленоидов, создающих электрические и магнитные поля (рис. 4.11). Требования, предъявляемые к свойствам электронных пучков и их параметрам, определяются областью их применения. Можно провести следующую классификацию электронных пучков по их основным признакам:

•      интенсивные и слабые (по плотности тока);

•      нерелятивистские и релятивистские (по энергии частиц); 

•      осесимметричные и неосесимметричные (по признакам симметрии);

•      цилиндрический, ленточный и т.п. (по типу сечения).

Из-за того, что формирование интенсивных пучков и их транспортировка невозможны без компенсации сил объемного заряда, для предотвращения расплывания их поперечного сечения применяются различные методы фокусировки: газовая, электростатическая и магнитная. Физически любую систему, формирующую электронный пучок, можно условно разделить на четыре основные области (рис. 4.11).

 

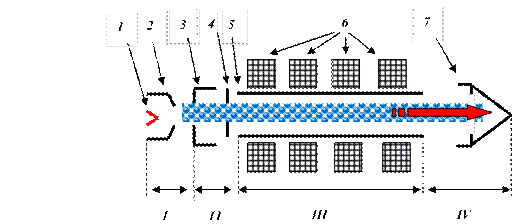
Рис. 4.11

I      – область электронного инжектора состоящего из накаливаемого катода 1, фокусирующего электрода 2 и анода 3. В электрическом поле электродов инжектора происходит первоначальное формирование электронного пучка;

II   – фокусирующая область  с линзами 4 ответственная за формирование пучка;

III                       – область дрейфового канала 5, в которой могут располагаться фокусирующая система 6, либо отклоняющие пучок системы. Их основная задача, препятствовать расширению электронного пучка для обеспечения максимально возможного токопрохождения; IV – приемник, или коллектор пучка 7. 

Рассмотрим вопросы, связанные с электростатической фокусировкой.

Задача состоит в нахождении электрических полей, образуемых системой электродов, и определение траекторий частиц в этих полях. Распределение потенциалов в свободном от зарядов пространстве находится путем решения уравнения Лапласа при заданных граничных условиях с заданной точностью. В случае движения параксиальных электронов в аксиально-симметричном электрическом поле можно считать, что потенциал в области пучка равен потенциалу на оси. В этом случае можно пренебречь поперечной составляющей скорости по сравнению с продольной. Тогда уравнение траекторий приводится d²r    dUzdr   r d²Uz

к    виду:         Uz^dz₂  _{2dz dz}  _{4 dz2}                ⁰_.    В    этом    уравнении    не

фигурируют заряд и масса, т.е. оно является параксиальным уравнением любых частиц в заданном поле. Линейность уравнений относительно dr d²r

r, dz ^, ₂ означает, что аксиально-симметричные поля являются dz электростатическими линзами, позволяющими фокусировать пучки заряженных частиц. Электростатические линзы подобно оптическим линзам обладают свойствами фокусировать или рассеивать проходящий сквозь них пучок заряженных частиц. 

Многообразие линз может быть разбито на три основных типа: одиночные, иммерсионные, линзы-диафрагмы. На рис. 4.12а представлена собирающая линза-диафрагма с круглым отверстием: электрод-диафрагма - 1; эквипотенциальные линии электростатического поля - 2; траектории параксиальных электронов - 3; фокус линзы - F.

                

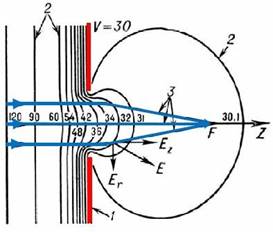
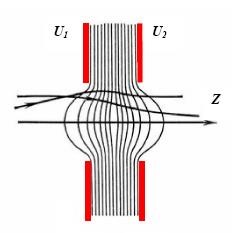
                                                   а                                                            б

Рис. 4.12

Однородное поле примыкает к диафрагме слева. При сечениях эквипотенциальных поверхностей проставлены соответствующие им значения потенциалов в произвольных единицах, принято, что потенциал равен нулю там, где равна нулю скорость частиц; потенциал электрода U= 30. Продольная составляющая напряженности электрического поля E_z тормозит электроны, поперечная составляющая E_r обеспечивает их фокусировку. На рис.  4.12б представлена иммерсионная линза, состоящая из двух диафрагм: тонкие линии — сечения эквипотенциальных поверхностей плоскостью рисунка; кривые со стрелками — траектории заряженных

частиц; U₁ и U₂ — потенциалы электродов.

Тонкая линза практически не изменяет расстояние траектории от оси, но скачком меняет наклон траектории. Фокусные расстояния тонких линздиафрагм (собирающих и рассевающих) могут быть определены из простого

                                         1          1

соотношения:       m  ^U₀₁ ^U₀₂ , где ^U₀ - потенциал в центре отверстия,

                                          f        4U₀

а ^U₀₁ и ^U₀₂^ - градиенты потенциала справа и слева от линзы. Для иммерсионных          линз отношение фокусных   расстояний          определяются ^{f    U}

формулой: ¹  ⁰² . Тогда для системы двух линз-диафрагм с фокусами

                                 f2                 U₀₁

^f₁ и ^f₂ и расстоянием l между линзами оптическая сила системы может быть

                                                                                1      1      1        l

определена из соотношения:                          

                                                                                 f      f1         f2          f1 f2 .

Рассмотрим теперь магнитную фокусировку. Транспортировка пучка заряженных частиц в продольном магнитном поле вследствие действия силы Лоренца приводит к уменьшению его расплывания. Если пренебречь коллективными взаимодействиями между частицами, то их траектории представляют собой спирали, навитые на магнитные силовые линии. Наличие объемного заряда существенно меняет характер движения частиц. 

При транспортировке аксиально-симметричного пучка с характеристиками:

r  const,z&  const, const,^U  0,^U  ^ r         необходимо     выполнение

                                                                           z        r       20

равенства, выражающего баланс сил электрического и магнитного поля

e U 1 e 2B2r. Подставляя в это выражение U   r , получим m r         4m r        2₀

 1 e B₂. Выполнение данного условия свидетельствует о том, что если 

₀ 2 m

пучок входит в область однородного магнитного поля с нулевыми значениями радиальной скорости и имеет однородное сечение объемной плотности заряда по сечению, то дальнейшее движение пучка будет равновесным. Полученный результат позволяет вычислить индукцию магнитного поля, необходимую для поддержания равновесного потока с



данным током I и радиусом r: B ^, где U_a – потенциал





металлического дрейфового канала, в котором распространяется пучок. В случае электронного пучка данное значение магнитной индукции получило название бриллюэновского магнитного поля, а ее величина при подстановке

1

830 I ²

численных значений составляет: ^B_Брил , [Гс, см, А, В]. Равновесный r U_a

1

830 I ²

пучок имеет радиус ^r_Брил  B U_{a 1}4 . Таким образом, для сохранения

начальных поперечных размеров пучка необходимы магнитные поля с большим значением индукции. 

Заряженные частицы эффективно фокусируются магнитными линзами. Простейшей магнитной линзой является короткий соленоид, фокусное расстояние которого пропорционально длине области, занятой магнитным полем. Уменьшение фокусного расстояния магнитной линзы достигается помещением соленоида в толстостенный железный экран с полюсными наконечниками (рис. 4.13а), где 1 – соленоид, 2 - панцырь, служащий магнитопроводом, 3 – полюсные наконечники. 

 

 

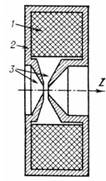
                                                   а                                                            б

Рис. 4.13

В этом случае магнитное поле будет сосредоточено между полюсными наконечниками, которые концентрируют магнитное поле на небольшом участке вблизи оптической оси линзы z.

Осесимметричные линзы обладают так называемой «мягкой фокусировкой». Квадрупольные линзы (рис. 4.13б), формирующие магнитные поля, направленные поперек движения частиц,

характеризуются «жесткой фокусировкой». Необходимые конфигурация и градиент магнитного поля  2 достигаются путем пропускания тока в обмотке  1. В ряде случаев полюсные наконечники изготавливают на основе постоянных магнитов. Как видно из рис. 4.13б, соседние полюса таких магнитных систем имеют противоположные полярности, а противоположные – одинаковые. Следует отметить, что на частицы, проходящие сквозь квадрупольную линзу, действующая сила Лоренца фокусирует их лишь в одной плоскости и дефокусирует в перпендикулярной. Поэтому для фокусировки в обеих плоскостях используют две линзы, повернутые относительно друг друга вокруг оси на 90⁰ . Для устранения астигматизма используют линзы с различными фокусными расстояниями. Вторая по направлению движения пучка линза должна обладать меньшим фокусным расстоянием (более сильная).

 

4.7. Электронно-оптические системы анализаторов

Построение электронно-оптических систем для управления движением пучков заряженных частиц широко используется в различных областях науки и техники. Особое место занимают системы с пространственным управлением положения пучка, которое осуществляется с помощью электрических (электростатическая отклоняющая система) и магнитных (магнитная отклоняющая система) полей. Такие системы широко используются в электровакуумных приборах, электроннолучевых технологиях и различных типах спектрометров. В энергоанализаторах и масс-спектрометрах используются физические принципы, связанные с отклонением заряженных частиц в статических электростатическом и/или магнитном поле, а также при наличии внешних ВЧ-полей. Наиболее распространенным примером с электростатическим управлением отклонения луча является электронно-лучевая трубка (ЭЛТ), при помощи которой традиционно изучают процессы управления электронным потоком. Электронно-оптическая система ЭЛТ (рис. 4.14а) состоит из иммерсионного объектива, фокусирующей системы и системы ускорения. Отклоняющая система ЭЛТ, представляет собой две пары X- и Y-пластин с однородным электрическим полем. На принципе отклонения заряженных частиц в электростатическом поле может быть реализован энергоанализатор. Отклонение и фокусировка пучка заряженных частиц достаточно эффективно реализуется при помощи секторного цилиндрического

                                                                                                                                                                       r    K

конденсатора (рис. 4.14б), у которого электрическое поле E ~      , где для r

цилиндрического конденсатора K _ U^{2 U1} (R₁ и R₂ – радиусы электродов

lnR2 R₁_

конденсатора 1). Через узкую выходную щель 3 будут проходить частицы, имеющие круговые траектории и скорости, удовлетворяющие условию: m2

qE .

R

Принцип разделения частиц по массам может быть также реализован в электростатических системах. Действие так называемого панорамного массспектрометра основано на разделении ионов, колеблющихся в электростатическом поле с параболическим распределением потенциала

(рис. 4.14в).

 

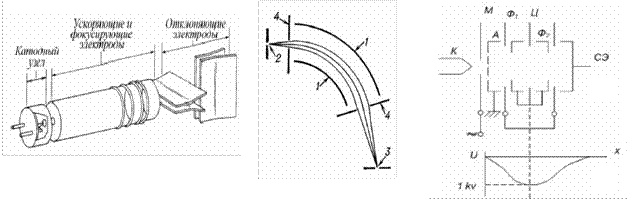
                                   а                                         б                                       в

Рис. 4.14

Электроны, эмиттированные катодом К, переходят через модулирующий электрод М, на который подается ВЧ-напряжение, модулирующее электронный ток по интенсивности и, в силу выбранного распределения потенциалов, колеблются около электрода А. В результате импульсной ионизации газа образуются сгустки ионов, которые колеблются в электрическом поле пространства дрейфа (Ф₁, Ф₂), причем частота колебаний

ионов f определяется их удельными массами f  ^{k qU} m , где U - напряжение на центральном электроде электростатического поля с параболическим распределением потенциала, k – коэффициент, зависящий от геометрии анализатора. Сгусток ионов, частота колебаний которого совпадает с частотой напряжения модулирующего электрода, называется резонансным и наводит на сигнальном электроде (СЭ) напряжение собственной частоты. Анализ ионов по массам заключается в измерении частот сигнальных напряжений узкополосным усилителем. 

Зависимость радиуса вращения частицы в магнитном поле от скорости и ее массы широко используется при построении анализаторов заряженных

 

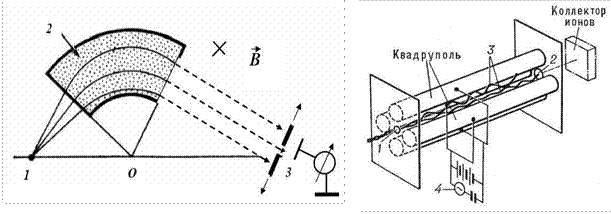
                                                        а                                                             б

Рис. 4.15

частиц по энергиям и массам.

                Принцип    одного    из     возможных    способов    реализации     масс-

спектрометра по такой системе показан на рис. 4.15а. Положительные ионы, образованные путем электрон-ионных столкновений, ускоряются в источнике ионов (1) одной разностью потенциалов, в результате чего приобретают скорость ~ ^qm и попадают в пространство дрейфа (2), где на них действует поперечное магнитное поле с индукцией В. Из условия

m2

равенства    сил      qB    можно    найти    радиус    траектории    иона

                                                       R             

             1         ^m        Таким     образом,     в     результате     взаимодействия     с

R  B    2^U    q .

магнитостатическим полем на коллектор (3) попадают только те ионы, радиус траекторий, которых соответствует положению щели в диафрагме перед коллектором. 

                Высокочастотные       системы      сепарации      приобрели      широкое

распространение в виду их малогабаритности и надежности. Рассмотрим типичные схемы квадрупольного и омегатронного масс-анализаторов. Квадрупольные масс-спектрометры, схематическое устройство которых представлено на рис. 4.15б, а фотография общего вида на рис. 4.16, достаточно широко распространены  благодаря высокой чувствительности, быстродействию, и широкому диапазону измерений. Данный тип массспектрометра используется в лабораториях специального физического практикума для изучения принципа его работы и применяется в научно исследовательской работе. 

 

Рис. 4.16.

Принцип действия прибора основан на разделении ионов по массам в ВЧ-квадрупольном электрическом поле, создаваемом между четырьмя параллельными стержнями круглого сечения (рис. 4.15б). Стержни электрически попарно соединены и на них подается напряжение

U^_

U  U_{_} U_~ cost;     const . Образующиеся ионы, транспортируются в  U_~

квадрупольный анализатор и, проходя вдоль него, совершают колебания под действием ВЧ-поля. Амплитуда колебаний ионов зависит от удельной массы иона m/q и величины напряжения на стержнях. При определенных параметрах квадруполя через анализатор могут пройти ионы только определенной массы. Массовое число ионов, имеющих устойчивую траекторию, связано с параметрами поля квадруполя следующим

соотношением: M _ 1.39f^₂¹⁰r₀₂^5U , где  f - частота (мГц), U – амплитуда ВЧ

поля [В], r₀ – геометрический масштаб поля (м). Для ионов других масс амплитуда колебаний неограниченно возрастает и они теряют заряд на стержнях. Развертка спектра масс осуществляется изменением напряжения на стержнях анализатора,  при этом отношение постоянной составляющей напряжения к амплитуде ВЧ-составляющей остается неизменным.

Существует еще один тип малогабаритного радиочастотного массспектрометра – омегатрон, принципиальная схема которого показана ниже. Молекулы находящегося в омегатроне газа ионизируются электронным пучком, проходящем вдоль оси анализатора и фокусирующего магнитного поля (рис. 4.17а). Под воздействием магнитного поля В и перпендикулярного к нему ВЧ-электрического поля, образовавшиеся ионы вращаются вокруг оси анализатора. Ионы, для которых частота вращения в данном магнитном поле совпадает с частотой приложенного ВЧ-напряжения, ускоряются ВЧ-полем и, двигаясь по раскручивающейся спирали, достигают коллектора ионов. 

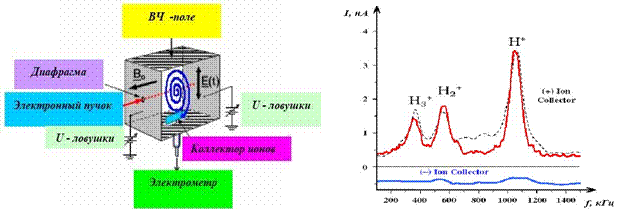
                                                        а                                                              б

Рис. 4.17

Измерение ионного тока, приходящего на коллектор, осуществляется

электрометрическим усилителем. Частота резонансного иона f  ^ , где

                                                                                                                                                                                      2

Bq

   - циклотронная частота. Ввиду того, что в постоянном магнитном m m

поле       const шкала массовых чисел спектрометра при развертке q  _,

приводится в единицах частоты. На рис. 4.17б приведен типичный вид масс-спектра.

4.8. Экспериментальные методы исследования. Пучковые технологии  Экспериментальное изучение пучков заряженных частиц связано с разработкой и применением разнообразных методов анализа собственных параметров пучков (ток, распределение плотности тока по сечению, энергетическое распределение и др.), а также формирующих их систем (инжектор, фокусирующие, транспортные и прочие системы). Условно все применяемые методы можно разделить на две основные группы: прямые и косвенные. 

К прямым относятся диагностические методы непосредственного измерения собственных параметров пучков, где применяются разнообразные конструкции широко распространенных средств: коаксиальные зонды, пояс Роговского, цилиндр Фарадея, метод вибрирующего зонда, метод подвижного коллектора с малым отверстием. Достаточно часто применяются методы использующие специально разработанные для анализа пучков электронно-оптические системы (энергоанализаторы, зарядовое и пространственное разделение).

Взаимодействие пучков частиц со средой приводит к разнообразным изменениям в ней и достаточно часто сопровождается ионизационными и радиационными эффектами. Анализ характеристик возникших изменений достаточно часто несет обширную информацию о характеристиках пучков и служит основанием для проведения косвенных измерений их параметров. К таки методам можно отнести измерения в области теплового и оптического излучения, вторичной электронной эмиссии и возникающего рентгеновского излучения, а также методы ионизации газа и стимулирования проводимости полупроводниковых структур. 

Особенности взаимодействия потоков электронов с конденсированными и газообразными веществами позволили осуществить новые технологические процессы, связанные с изменением исходных физико-химических свойств материалов, подвергающихся воздействию пучков: облучение полимерных материалов, сопровождающееся перестройкой молекулярных связей и изменением механической прочности, температуростойкости, электронная литография и др. Интенсивные пучки электронов с высокой мощностью применяются для «чистой» плавки металлов, резки и сварки тугоплавких металлов. Воздействие импульсных пучков дает возможность эффективно воздействовать на свойства поверхностных и приповерхностных слоев металлов, изменяя их структурный и фазовый состав. При помощи хорошо сфокусированных электронных пучков реализуются различные электронно-зондовые методы структурного и элементного анализа состава веществ и материалов, таких как просвечивающая и растровая электронная микроскопия, малоугловое рассеяние рентгеновского излучения, масс-спектрометрия и др.