Лекции на повторение школьного курса математики

Урок 14.  Тригонометрические функции углового аргумента

Цели урока:  ввести понятие тригонометрической функции углового аргумента; ввести понятие радианной меры угла; формировать умение переводить радианную меру угла в градусную и наоборот.

Ход урока 

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

                    II. Проверка домашнего задания.

Опрос по теории:

1. Какие меры угла вы знаете?

2. Чему равен 1 градус?

3. Чему равен 1 радиан?

4. Сколько радиан в 1 градусе?

5.  Сколько градусов в 1 радиане?

6. Как перевести градусную меру в радианную?

7. Как перевести радианную меру в градусную?

Затем вызываются к доске два учащихся для обобщения теоретического материала.

III.  Закрепление нового материала.

                Решение у доски с полным пояснением и ответами на вопросы по теории заданий №135, 137, 139, 141, 142, 144.

                      IV. Проверочная работа.

Вариант №1	Вариант №2
1. Переведите данные числа из радианной меры в градусную: ; ; ; .	1. Переведите данные числа из радианной меры в градусную: ; ; ; .
2. Переведите данные числа из радианной меры в градусную: .	2. Переведите данные числа из радианной меры в градусную: .
Вариант №3	Вариант №4
1. Переведите данные числа из радианной меры в градусную: ; ; ; .	1. Переведите данные числа из радианной меры в градусную: ; ; ; .
2. Переведите данные числа из радианной меры в градусную: .	2. Переведите данные числа из радианной меры в градусную: .

Подведение итогов.

Домашнее задание: №136, 138, 140, 143.

Урок 15. Формулы приведения

Цели урока:  вывести формулы приведения; рассмотреть задания на применение этих формул.

Ход урока 

I.   Организационный момент.

Приветствие, сообщение темы и задач урока.

II.  Объяснение нового материала.

Объяснение нового материала (стр. 43-45):

1. Рассмотреть выражения под знаком тригонометрической функции в формулах приведения.

2. Вспомнить формулы, выведенные ранее, говоря о свойствах синуса, косинуса, тангенса и котангенса.

3. Провести анализ этих формул и составить схему-конспект по теме «Формулы приведения».

Формулы приведения

Выражения под знаком тригонометрической функции

Выражения под знаком тригонометрической функции, при которых наименование функции не меняется

Выражения под знаком тригонометрической функции,  при которых наименование функции меняется

Знаки преобразуемых тригонометрических функций

и

4. Рассмотреть примеры , , .

 III. Закрепление нового материала.

Решаются задания из №151-154 в тетрадях, с полным комментарием.

                   IV. Решение заданий.

Учитель решает (а) в заданиях №155-157, №159, объясняя еще раз как применять формулы приведения. Затем один учащийся из группы Б решает у доски (б) в тех же номерах. И, наконец, все решают самостоятельно (в) в тех же номерах.

Подведение итогов.

Домашнее задание: №155-157 (г), №159 (г)); теория в учебнике

стр. 43-45.

Урок 16. Функция , ее свойства и график

Цели урока:  рассмотреть график функции; сформулировать свойства функции.

Ход урока

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

                   II.   Проверочная работа.

Вариант 1	а	№158	№160
Вариант 2	б

III.  Объяснение нового материала.

Объяснение нового материала по схеме-конспекту  (стр. 46-49):

1. Рассмотреть схему-конспект и описать основные свойства.

2.  Рассмотреть свойство нечетности функции.

3.  Рассмотреть свойство возрастания и убывания функции.

4. Описать основные свойства функции, не выполняя построения самого графика.

Основные свойства функции
Свойства функции	Свойства функции
Во всех следующих свойствах считаем, что
-- возрастает на	-- возрастает на
-- убывает на	-- убывает  на
,	,
,	,

IV.   Закрепление нового материала.

Не выполняя построения графика, опишите свойства функций:

1) ; 2) ; 3) ;

4) .

              V.  Решение заданий по теме.

Решение заданий из №168-170.

Подведение итогов.

Домашнее задание: №171-173; теория в учебнике стр. 46-49.

Урок 17. Функция , ее свойства и график

Цели урока:  сформировать умения: зная график функции , строить графики функций ,  .

Ход урока

                          I.      Организационный момент.

Приветствие, сообщение темы и задач урока.

                       II.      Проверка домашнего задания.

Проверить домашнюю работу можно: провести проверочную работу; приготовить карточки и в течение урока давать их как дополнительное задание, для получения оценки.

Вариант №1	Вариант №2
1. Упростить выражение	1. Упростить выражение
2. Не выполняя построения, определите, принадлежит ли графику функции точка: .	2. Не выполняя построения, определите, принадлежит ли графику функции точка: .
Вариант №3	Вариант №4
1. Упростить выражение	1. Упростить выражение
2. Не выполняя построения, определите, принадлежит ли графику функции точка: .	2. Не выполняя построения, определите, принадлежит ли графику функции точка: .

III. Объяснение нового материала.

Объяснение нового материала (стр. 49-50):

IV. Закрепление нового материала.

В одной системе координат построить графики функций одной группы и описать их свойства:

1) , , , .

Обобщить преобразования графиков функций сдвигом по оси .

В одной системе координат построить графики функций одной группы и описать их свойства:

1) , , , ,

Обобщить преобразования графиков функций сдвигом по оси .

Решить задания из №176 и описать свойства функций.

V. Проверочная работа.

Для учащихся группы A:

Вариант №1	Вариант №2
1. Постройте график функции ; 2. Укажите область значений данной функции; 3. Найдите наибольшее и наименьшее значения функции на интервале	1. Постройте график функции ; 2. Укажите область значений данной функции; 3. Найдите наибольшее и наименьшее значения функции на полуинтервале

Для учащихся группы Б:

Вариант №3	Вариант №4
1. Постройте график функции ; 2. Укажите область значений данной функции; 3. Найдите наибольшее и наименьшее значения функции на отрезке	1. Постройте график функции ; 2. Укажите область значений данной функции; 3. Найдите наибольшее и наименьшее значения функции на полуинтервале

Подведение итогов.

Домашнее задание: №174 (г), 175 (г), 178; теория в учебнике стр. 49-50.

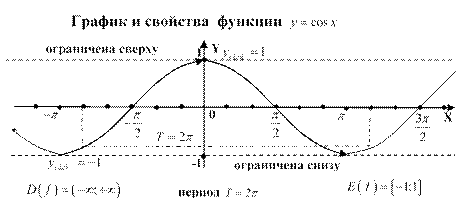
Урок 18. Функция , ее свойства и график

Цели урока: рассмотреть график функции; сформулировать свойства функции.

Ход урока: 

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

II.  Математический диктант.

Вычислите при помощи формул приведения:

1) .

2) .

3) .

4) .

 

III. Объяснение нового материала.

Объяснение нового материала (стр. 51-52):

1.  Рассмотреть схему-конспект и описать основные свойства.

2.  Рассмотреть свойство четности функции.

3.  Рассмотреть свойство возрастания и убывания функции.

4. Описать основные свойства функции, не выполняя построения самого графика.

Основные свойства функции
Свойства функции	Свойства функции
Во всех следующих свойствах считаем, что
-- возрастает на	-- возрастает на
-- убывает на	-- убывает  на
,	,
,	,

IV.   Закрепление нового материала.

Не выполняя построения графика, опишите свойства функций:

1) ; 2) ; 3) ;

4) .

V.  Решение заданий по теме.

Решение заданий из №195-200.

Подведение итогов.

Домашнее задание: №201, 202; теория в учебнике стр. 51-52.

Урок 19. Функция , ее свойства и график

Цели урока:  сформировать умения: зная график функции , строить графики функций , 

Ход урока

I.   Организационный момент.

Приветствие, сообщение темы и задач урока.

II. Объяснение нового материала.

Объяснение нового материала (стр. 52-53):

1. Рассмотреть построенные ранее в одной системе координат  графики функций , , , , , где за и взять конкретные числа.

2. Проанализировать аналогичные построения  в одной системе координат  графики функций , , , , .

 III. Закрепление нового материала.

В одной системе координат построить графики функций одной группы и описать их свойства:

1) , , , .

Обобщить преобразования графиков функций сдвигом по оси .

В одной системе координат построить графики функций одной группы и описать их свойства:

1) , , , ,

Обобщить преобразования графиков функций сдвигом по оси .

Решить задания из №205 (а, б) и описать свойства функций.

IV. Проверочная работа.

Для учащихся группы A:

Вариант №1	Вариант №2
1. Постройте график функции ; 2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции.	1. Постройте график функции ; 2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции.

Для учащихся группы Б:

Вариант №3	Вариант №4
1. Постройте график функции ; 2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции.	1. Постройте график функции ; 2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции.

Подведение итогов.

Домашнее задание: №203, №204 (в, г), №205 (в, г); теория в

 учебнике стр. 52-53.

Урок 20. Периодичность функций  ,

Цели урока:   ввести понятие основного периода; научить находить основной период функции.

I.   Организационный момент.

Приветствие, сообщение темы и задач урока.

II.  Объяснение нового материала.

Объяснение нового материала (стр. 54-55):

1. Ввести понятие период функции.

2.Обобщить метод построения графиков функций  и .

3.Ввести формулу нахождения основного периода функций .

III.  Закрепление нового материала.

Решение заданий из №217, 219.

                   IV. Проверочная работа.

Вариант №1	Вариант №2
1. Докажите, что число  является периодом функции .	1. Докажите, что число  является периодом функции .
2. Найдите наименьший положительный период функции	2. Найдите наименьший положительный период функции
Вариант №3	Вариант №4
1. Докажите, что число  является периодом функции .	1. Докажите, что число  является периодом функции .
2. Найдите наименьший положительный период функции	2. Найдите наименьший положительный период функции

Подведение итогов.

Домашнее задание: №218, 220, 221; теория в учебнике стр. 54-55.

Задание на дополнительную оценку: Постройте график и опишите свойства функций  и , где  и .