Лекционный материал «неопределенный интеграл и его свойства. Таблица интегралов. Непосредственное интегрирование»

Лекция 11 «неопределенный интеграл и его свойства. Таблица интегралов. Непосредственное интегрирование»

Итак, начинаем с простого. Посмотрим на таблицу интегралов. Как и в производных, мы замечаем несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций. Нетрудно заметить, что любой табличный интеграл (да и вообще любой неопределенный интеграл) имеет вид:

Сразу разбираемся в обозначениях и терминах:

– значок интеграла.

 – подынтегральная функция (пишется с буквой «ы»).

 – значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.

 – подынтегральное выражение или «начинка» интеграла.

 – первообразная функция.

 – множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа .

Решить интеграл – это значит найти определенную функцию , пользуясь некоторыми правилами, приемами и таблицей.

Еще раз посмотрим на запись:

Посмотрим в таблицу интегралов.

Что происходит? Левые части  у нас превращаются в другие функции: .

Упростим наше определение.

Решить неопределенный интеграл  – это значит ПРЕВРАТИТЬ его в определенную функцию , пользуясь некоторыми правилами, приемами и таблицей.

Возьмем, например, табличный интеграл . Что произошло?  превратился в функцию .

Как и в случае с производными, для того, чтобы научиться находить интегралы, не обязательно быть в курсе, что такое интеграл, первообразная функция с теоретической точки зрения. Достаточно просто осуществлять превращения по некоторым формальным правилам. Так, в случае  совсем не обязательно понимать, почему интеграл превращается именно в . Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны.

Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найдена правильно, справедливо следующее:

Иными словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.

Вернемся к тому же табличному интегралу .

Убедимся в справедливости данной формулы. Берем производную от правой части:

 – исходная подынтегральная функция.

Вот, кстати, стало понятнее, почему к функции  всегда приписывается константа . При дифференцировании константа всегда превращается в ноль.

Решить неопределенный интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию. В рассматриваемом табличном примере , , ,  и т. д. – все эти функции являются решением интеграла . Решений бесконечно много, поэтому записывают коротко: 

Таким образом, любой неопределенный интеграл достаточно легко проверить (в отличие от производных, где хорошую стопудовую проверку можно осуществить разве что с помощью математических программ). Это некоторая компенсация за большое количество интегралов разных видов.

Переходим к рассмотрению конкретных примеров. Начнем, как и при изучении производной, 
с двух правил интегрирования, которые также называют свойствами линейностинеопределенного интеграла:

 – постоянный множитель можно (и нужно) вынести за знак интеграла.

 – интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.

Как видите, правила, в принципе, такие же, как и для производных.

Таблица

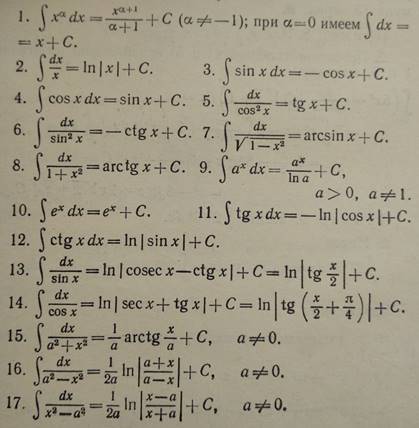
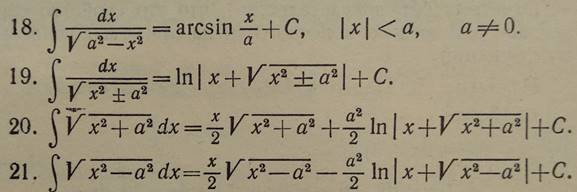
В классе

№8.14

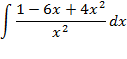
Разделив числитель на знаменатель получаем:

№8.48

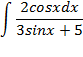
Выражение cosx подведем под знак дифференциала, т.е.  . Следовательно

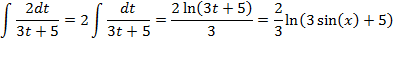
№8.52

№8.47

На дом

№8.13

№8.25

№8.35

Пусть , тогда . Следовательно

Скачано с www.znanio.ru