Лекция № 7 Основные законы алгебры логики

Лекция № 7

Основные законы алгебры логики

1. Законы алгебры логики

В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений. Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствии с законами логики.

 - закон тождества (всякое высказывание тождественно самому себе)

   - переместительный (коммутативный) закон (можно менять местами логические переменные при операциях логического умножения и логического сложения)

  - сочетательный (ассоциативный) закон (если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять)

  - распределительный (дистрибутивный) закон (можно выносить за скобки как общие множители, так и общие слагаемые).

  - закон идемпотентности

  - формулы де Моргана

  - закон поглощения

 - закон двойного отрицания (если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание).

 - закон контрапозиции

 - закон исключения третьего (высказывание может быть либо истинным, либо ложным, третьего не дано. Результат логического сложения высказывания и его отрицания всегда принимает значение истина.)

 - закон непротиворечия (высказывание не может быть одновременно истинным и ложным. Если высказывание А – истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.)

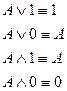 -  законы исключения констант

 - закон транзитивности

Рассмотрим в качестве примера применения законов логики и правил алгебры логики преобразование логического выражения.

Пример: упростить формулу

  (сначала используем закон дистрибутивности, затем – закон операции с константами)

2. Решение логических задач

Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, т.е. записать на языке алгебры высказываний. Полученные логические выражения необходимо упростить и проанализировать. Для этого иногда бывает необходимо построить таблицу истинности полученного логического выражения.

Пример логической задачи. Кто из учеников A, B, C и D играет, а кто не играет в шахматы, если известно следующее:

а) если А или В играет, то С не играет;

б) если В не играет, то играют С и D;

в) С играет?

Решение задачи: Определим следующие простые высказывания:

А – «ученик А играет в шахматы»;

В – «ученик В играет в шахматы»;

С – «ученик С играет в шахматы»;

D – «ученик D играет в шахматы».

Запишем сложные высказывания, выражающие известные факты:

а)

б)

в) С

Запишем произведение указанных сложных высказываний:

Упростим эту формулу:

=

Отсюда А = 0, В = 0, С = 1, D = 1.

Ответ: в шахматы играют ученики С  и D, а ученики А и В – не играют.