Лекция "Понятие о ЦМР"

Тема 1.

1.1. Понятие о ЦМР

Под цифровой моделью рельефа (ЦМР) принято понимать средство цифрового представления трехмерных пространственных объектов (поверхностей, или рельефов) в виде трехмерных данных, образующих множество высотных отметок (отметок глубин) и иных значений аппликат (координаты Z) в узлах регулярной или нерегулярной сети или совокупность записей горизонталей (изогипс, изобат) или иных изолиний.

Цифровая модель рельефа (ЦМР, Digital terain model, DTM; digital elevation model, DEM; Digital Terrain Elevation Data, DTED). Наиболее распространенными способами цифрового представления рельефа является растровое представление и особая модель пространственных данных, основанная на сети TIN и аппроксимирующая рельеф многогранной поверхностью с высотными отметками (отметками глубин) в узлах треугольной сети. Ряд исследователей и направлений различают цифровые модели высот (DEM (1)) и производные от них цифровые модели рельефа (DTM); в этом случае под последними понимается совокупность производных морфометрических показателей; необходимость различения связана отчасти с наименованием и содержанием американского стандарта на ЦМР (DEM (2)); многозначность слова "terrain" является также основанием для его истолкования и использования в сочетании "digital terrain model" как цифровых моделей местности, закрепленном в "ГОСТ 22268-76. Геодезия. Термины и определения"; развитие методов создания ЦМР путем обработки изображений на цифровых фотограмметрических станциях привело к появлению термина "цифровая модель поверхности" (DSM) как ее первичного продукта, нуждающегося в "рафинировании".

Процесс цифрового моделирования рельефа включает создание ЦМР, их обработку и использование.

Обработка ЦМР служит для получения производных морфометрических или иных данных, включая вычисление углов наклона и экспозиции склонов; анализ видимости/невидимости; построение трехмерных изображений, в том числе блок-диаграмм; профилей поперечного сечения; оценку формы склонов через кривизну  их поперечного и продольного сечения, измеряемую радиусом кривизны главного нормального сечения или ее знаком, т.е. выпуклостью/вогнутостью; вычисление (положительных и отрицательных) объемов; генерацию линий сети тальвегов  и водоразделов; цифровое ортотрансформирование при цифровой обработке изображений и другие вычислительные операции и графоаналитические построения. Методы и алгоритмы создания и обработки ЦМР применимы к иным физическим или статистическим рельефам и полям: погребенному рельефу, барическому рельефу и т.п.

Первые эксперименты по созданию ЦМР относятся к самым ранним этапам развития геоинформатики и автоматизированной картографии первой половины 60-х годов XX в. С тех пор разработаны методы и алгоритмы решения различных задач, созданы программные средства моделирования, крупные, в том числе национальные и глобальные, массивы данных о рельефе, накоплен опыт решения с их помощью разнообразных научных и прикладных задач.

Различают четыре типа исходных множеств опорных точек, используемых для построения ЦМР: 1) нерегулярно расположенных точек; 2) нерегулярно расположенных точек, положение которых связано со структурой рельефа (структурные линии); 3) точек, регулярно расположенных вдоль линий, слабо связанных со структурой поля (на изолиниях или профилях); 4) регулярно расположенных точек.

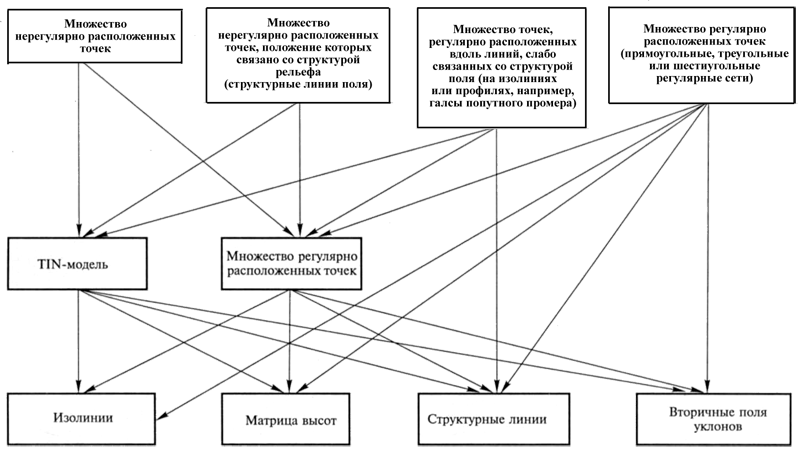
Рис.1.1 Общая схема создания ЦМР [Преамбула Е. Г. Капралова к ст. О. Р. Мусина, 1998]

1.2. Источники данных для построения ЦМР

Источниками исходных данных для создания ЦМР суши служат топографические карты, аэрофотоснимки, космические снимки и другие ДДЗ, данные альтиметрической съемки, спутниковых систем позиционирования, нивелирования и других методов геодезии; подводного рельефа акваторий (батиметрии) – морские навигационные карты, данные промерных работ, эхолотирования, в том числе с использованием гидролокатора бокового обзора; рельефа поверхности и ложа ледников – аэросъемка, материалы фототеодолитной и радиолокационной съемки. Среди перечисленного разнообразия источников данных для моделирования рельефа двум из них – картам и аэрокосмическим материалам – принадлежит особая роль массовых источников.

Роль данных дистанционного зондирования как источника данных для построения ЦМР по разным причинам будет расти, а доля и роль карты — снижаться. Это технологические и технические причины: рост пространственного разрешения систем сканерной съемки (до 1 м и менее), широкое распространение относительно недорогих и доступных цифровых фотограмметрических станций, в том числе на платформе персональных компьютеров, появление принципиально отличного от стереофотограмметрического метода экстракции высот — интерферометрии, известной в приложениях к обработке радиометрических данных. Аэроснимки широко используются для контроля качества и верификации ЦМР. С их относительно крупномасштабной стереомодели, принимаемой за условно истинную, берутся контрольные точки со значениями высотных отметок, точность которых заведомо намного выше, чем у верифицируемой модели. Данные дистанционного зондирования в целом и процедуры их обработки, в том числе экстракции высот, тоже не лишены недостатков. В условиях плотной городской застройки или высокой залесенности (при стопроцентной сомкнутости крон древостоя) полученная цифровая модель в существенной своей части будет отражать геометрию зданий и сооружений или полога леса и требовать вмешательства оператора в автоматизированый процесс ее построения.

Карта остается, бесспорно, основным источником данных для ЦМР, на чем стоит остановиться подробней. К картографическим источникам принадлежат топографические карты и планы, используемые для создания ЦМР суши, и морские навигационные или топобатиметрические карты для ЦМР акваторий. Типовая технология генерации ЦМР основана на цифровании горизонталей как основной ее составляющей, а также высотных отметок и других картографических элементов, используемых для отображения рельефа, с привлечением данных по другим объектам карты (элементов гидрографической сети). При наличии готовой цифровой топографической или аналогичной ей карты используются соответствующие им слои.

Как источник данных для ЦМР, топографическая карта при всех ее достоинствах не лишена недостатков. Один из них связан с изображением рельефа горизонталями. Важный практический вывод, следующий из анализа мелкомасштабных общегеографических карт, заключается в том, что топографические и иные карты суши масштаба 1:500 000 и мельче практически непригодны для создания ЦМР. Как и любой другой элемент картографического изображения, горизонтали проведены на нем с определенной точностью, которая при прочих равных условиях (масштабе, методах съемки или составления карты путем генерализации крупномасштабных картографических источников) зависит от типа, морфологии рельефа. Кроме основных топографические карты содержат дополнительные и вспомогательные горизонтали. Первые из них проводятся на половине высоты сечения и носят также название полуторизонталей и с точки зрения метричности аналогичны основным, вторые же проводятся, согласно инструкциям, на произвольной высоте и, как правило, должны быть надписаны; в противном же случае их учет при построении ЦМР невозможен. Кроме того, топографические карты лишены изображения рельефа дна внутренних водоемов и морских и океанических акваторий. Отсюда общая рекомендация к программным средствам создания ЦМР: они должны поддерживать контроль геометрической корректности цифровых представлений горизонталей, т. е. соблюдение двух условий: 1) одноименные и разноименные горизонтали не должны пересекаться (сливаться, касаться)¹; 2) каждая горизонталь должна быть замкнута на самое себя или границу картографического изображения (обычно рамку карты). Соблюдение первого из условий обеспечивает отсутствие складок (нахлестов) в записи горизонтали и слияния (касания) разноименных (соседних) горизонталей, второе — отсутствие в них разрывов.

Недостатки топокарт в части изображения рельефа горизонталями отчасти могут быть компенсированы другими графическими элементами, используемыми для отображения элементов и форм рельефа, не выражаемых в горизонталях по чисто графическим или содержательным мотивам. К примеру, свод условных знаков топографических карт масштаба 1:10 000 содержит более 50 линейных и точечных знаков, часть из которых — высотные отметки, отметки урезов воды, знаки оврагов с указанием их глубины, обрывов, карстовых воронок и других природных образований, а также ряда искусственных форм рельефа — действительно способны существенно улучшить общую метрическую характеристику рельефа и повысить точность создаваемой модели путем их учета в структурных ЦМР.

1.3. Типы цифровых моделей рельефа

Обычно первичные данные существуют или с использованием тех или иных операций приводятся к одному из двух наиболее широко распространенных представлений поверхностей (полей) в ГИС: растровому представлению (модели) и модели TIN.

Растровые ЦМР представляют собой матрицу высот: регулярную (обычно квадратную) сеть высотных отметок в ее узлах, расстояние между которыми (шаг) определяет ее пространственное разрешение. Преимущество такой модели — в удобстве ее компьютерной обработки. В последнее время довольно часто для обозначения таких моделей используется термин GRID (грид). К растровой, или как ее чаще называют матричной или регулярной, модели путем интерполяции, аппроксимации, сглаживания и иных трансформаций могут быть приведены ЦМР всех иных типов, что чаще всего и делается на практике. Для восстановления поля высот в любой его точке (например, в узле регулярной сети) по заданному множеству высотных отметок (например, по цифровым записям горизонталей) обычно применяются разнообразные методы интерполяции. Среди них наиболее употребительными считаются метод кригинга, средневзвешенная интерполяция по методу Шепарда, полиномиальное и кусочно-полиномиальное сглаживание.

Суть модели TIN в ее наименовании — «Нерегулярная треугольная сеть» (в английском оригинале — Triangulated Irregular Network). В своем пространственном выражении — это сеть треугольников — элементов триангуляции Делоне — с высотными отметками в ее узлах, что позволяет представить моделируемую поверхность как многогранную. Триангуляцией Делоне для множества точек S  на плоскости называют триангуляцию DT(S), такую что никакая точка A из S не содержится внутри окружности, описанной вокруг треугольника из DT(S), такого, что ни одной из вершин его не является точка A. Такая триангуляция максимизирует минимальный угол среди всех углов всех построенных треугольников, тем самым избегаются «тонкие» треугольники.

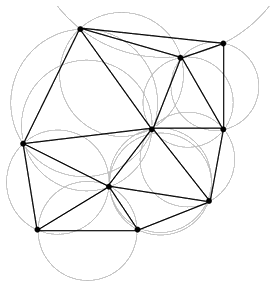
Рис.1.2 Триангуляция Делоне

Модель TIN поддерживается многими мощными универсальными программными средствами ГИС, модулями обработки и создания ЦМР в их составе. Таков, к примеру, модуль 3D Analyst в программных средствах ГИС Arclnfo (ESRI Inc., США). Однако ее использование в технологиях создания ЦМР на основе слоя оцифрованных горизонталей цифровых карт, массовое производство которых налажено большинством национальных топографо-картографических служб, вскрыло его существенные недостатки. Основной из них — «эффект террас», выражающийся в появлении морфологических артефактов — плоских участков в заведомо невозможной геоморфологической ситуации (например, по линии днища V-образных тальвегов). Одна из основных причин — в малости расстояний между точками цифровой записи горизонталей в сравнении с расстояниями между самими горизонталями, что характерно для большинства типов рельефа в их картографическом отображении. Появление таких морфологических артефактов нарушает морфографию и морфометрию моделируемого рельефа и снижает точность и качество самой модели и ее производных. Один из способов значительного улучшения качества и морфологического правдоподобия ЦМР состоит в расширении модели TIN путем ее структурирования — введения в нее сети тальвегов, водоразделов и линий разрывов (бровок, уступов террас и т.п.).

Обратной (двойственной) триангуляции Делоне являются полиномы Вороного. Эти фигуры образуются при соединении середин сторон треугольников, образовывающих триангуляционную сеть. Такие модели практически не используются для отображения рельефа. Большее применение полиномы Вороного нашли для моделирования погребенных поверхностей и создания каркасных моделей рудных тел в горно-геологических ГИС.

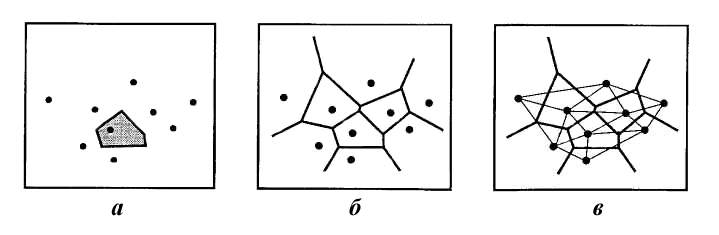
Рис. 1.3 Многоугольник Вороного (а), диаграмма Вороного (б), та же диаграмма Вороного и двойственная ей триангуляция Делоне (в)

Дальнейшее развитие цифрового моделирования рельефа связывается с новыми трехмерными моделями пространственных данных, известными пока лишь в экспериментах и немногих реализациях в коммерческих программных средствах ГИС. Эти модели основаны на трехмерных расширениях «планиметрических» двухмерных моделей. К ним принадлежат модель объемных пикселов — «вокселов» (трехмерное расширение растровой модели данных) и трехмерное расширение модели TIN — тетраэдрическая модель. Оба типа «истинно-трехмерных» моделей способны описывать не только поверхности, но и тела, заимствуя подходы и алгоритмы так называемого «твердотельного моделирования» в компьютерной графике. Известны примеры их использования в геологии, геофизике, маркшейдерии как инструмента «геометризации недр».

1.4. Математические алгоритмы, используемые при построении ЦМР

Создание ЦМР и пересчет их из одного вида в другой базируется на использовании математического аппарата. От правильного его применения зависит не только адекватность построенной модели, но и оптимальность затрат ресурсов машинной памяти и времени вычисления.

Среди основных групп алгоритмов выделяют:

• вычисление отметок высот в произвольных точках по исходному множеству нерегулярно расположенных точек;
• вычисление отметок высот в произвольных точках по исходным точкам, заданным триангуляцией Делоне;
• вычисление отметок высот в произвольных точках по исходным точкам, заданным на матрице высот.

Рассмотрим некоторые примеры таких алгоритмов.

Локальный интерполяционный алгоритм, построенный на триангуляции Делоне. Через три точки в пространстве проходит плоскость, уравнение которой является многочленом первой степени по своим переменным.

Метод скользящего окна (локальный интерполяционный алгоритм). Для получения значения z в точке с координатами х, у выполним следующий алгоритм.

1. Выберем из исходных точек те, которые расположены на плоскости аргументов на расстоянии, меньшем чем заданная величина R от точки с координатами (х,у). Обозначим номера этих точек t₁, t₂,…,t_i.

Если координаты одной из исходных точек, например точки (x_p,y_p), совпадают с координатами (x,y), то положим z=z_p.

В противном случае вычислим z по формуле z = (z_t1d_t1 + z_t2d_t2 + … + z_tid_ti)/(d_t1 + d_t2 + … + d_ti),

где d_ti – вес точки t_i, который может быть равен величине, обратной расстоянию между точкой (x,y) и точкой (x_ti,y_ti).

Метод весового среднего или модифицированный метод скользящего окна (локальный аппроксимационный алгоритм). Для получения значения z в точке с координатами х, у выполним следующий алгоритм.

1.   Выберем из исходных точек т те, которые расположены на плоскости аргументов ближе других от точки с координатами (x,y). Обозначим номера этих точек t₁, t₂,…,t_m.

2.   Вычислим z по формуле z = (z_t1d_t1 + z_t2d_t2 + … + z_imd_tm)/(d_t1 + d_t2 + … + d_tm),

где d_tm – вес точки t_m , который может быть равен величине, обратной расстоянию между точкой (х,у) и точкой (x_tm,y_tm) или быть некоторой степенью этой величины.

Глобальный интерполяционный алгоритм. Используется для восстановления значений функции в точке (х,у) по множеству всех n, исходных точек с использованием многочлена, число членов которого равно числу исходных точек.

В этом случае для определения коэффициентов многочлена необходимо решить систему n уравнений с n неизвестными:

a₁f₁(x_i,y_i) + a₂f₂(x_i,y_i) + … + a_kf_k(x_i,y_i)  = zi, i = 1, …, n,

где f₁(x_i,y_i) = 1, f₂(x_i,y_i) = x_i, f₃(x_i,y_i) = y_i, f₄(x_i,y_i) = x_i², f₅(x_i,y_i) = y_i² и т.д.

Глобальный аппроксимационный алгоритм. Применяется для восстановления значений функции в точке (х,у) по множеству

всех п исходных точек с использованием многочлена, число членов которого (k) не равно числу исходных точек. Коэффициенты определяются исходя из принципа наименьших квадратов:

или

Решение этой задачи эквивалентно решению следующей системы k линейных уравнений с k неизвестными a₁, a₂, a₃, …, a_k:

a₁Sum f₁(x_i,y_i) + a₂Sum (f₁(x_i,y_i) f₂(x_i,y_i)) + ... + a_kSum (f₁(x_i,y_i) f_k(x_i,y_i)) = Sum (z_if₁(x_i,y_i)),

a₁Sum (f₁(x_i,y_i) f₂(x_i,y_i)) + a₂Sum (f₂(x_i,y_i) f₂(x_i,y_i)) + ... + a_kSum (f₂(x_i,y_i) f_k(x_i,y_i)) = Sum (z_if₂(x_i,y_i)),

...
a₁Sum (f₁(x_i,y_i) f₃(x_i,y_i)) + a₂Sum (f₂(x_i,y_i) f₃(x_i,y_i)) + ... + a_kSum (f₃(x_i,y_i) f_k(x_i,y_i)) = Sum (z_if₃(x_i,y_i)),

Это только некоторые примеры из большого многообразия алгоритмов, используемых в различных задачах восстановления значений рельефа (функций) по множеству исходных точек, полученных в результате измерений.

1.5. Использование ЦМР

Готовая цифровая модель способна обеспечить решение самых разнообразных задач благодаря развитым функциям цифрового моделирования рельефа, которые встроены в современные универсальные полнофункциональные инструментальные программные средства ГИС.

Обычно функционально обособленные модули обработки ЦМР в составе таких программных продуктов поддерживают следующие группы функций:

• расчет «элементарных» морфометрических показателей: углов наклона (уклонов) и экспозиций склонов;
• оценка формы склонов через кривизну их поперечного и продольного сечений;
• генерация сети тальвегов и водоразделов (сепаратрисе) и других особых точек и линий рельефа, нарушающих его «гладкость»; подсчет положительных и отрицательных объемов относительно заданного горизонтального уровня в пределах границ участка;
• построение профилей поперечного сечения рельефа по направлению прямой или ломаной линии;
• аналитическая отмывка рельефа;
• трехмерная визуализация рельефа в форме блок-диаграмм и других объемных каркасных (нитяных), полутоновых (светотеневых) и фотореалистичных (текстурированных) изображений, в том числе виртуально-реальностных, например путем драпировки поверхности рельефа цифровыми космо- или аэрофотоизображениями;
• оценка зон видимости или невидимости с заданной точки (точек) обзора (анализ видимости/невидимости);
• построение изолиний по множеству отметок высот (например, генерация горизонталей);
• интерполяция значений высот, другие трансформации исходной модели (например, осреднение, сглаживание, генерализация, фильтрация и т.п.).
• ортотрансформирование аэро- и космических снимков.

Перечисленные функции стандартного коммерческого программного обеспечения ГИС, разумеется, не исчерпывают всех возможностей обработки данных о рельефе; в экспериментах и специализированных средствах обработки ЦМР они существенно богаче, образуя основу разнообразных приложений технологии цифрового моделирования рельефа.