ЛЕКЦИЯ.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

1) ОСНОВНЫЕ ПОНЯТИЯ

   Дифференциальным уравнением второго порядка называется уравнение, содержащее неизвестную (искомую) функцию у(х), независимую переменную х, первую и  вторую производные у', у'' или дифференциалы

   Дифференциальное уравнение второго порядка символически можно записать в общем виде следующим образом:

 или

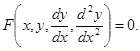
   Дифференциальное уравнение второго порядка, разрешенное относительно второй производной, имеет вид:

 или

   Решением дифференциального уравнения называется всякая функция, которая обращает его в тождество. Дифференциальное уравнение второго порядка имеет бесчисленное множество решений, которые можно представить в виде функции  Эта совокупность решений называется общим решением.

   Функция, получающаяся из общего решения при конкретных значениях постоянных С₁ и С₂, называется частным решением. Частное решение находится при помощи задания начальных условий: у(х=х₀)=у₀ и у'(х=х₀)=у₀', где х₀, у₀, у₀'– конкретные числа.

Задача отыскания частного решения  дифференциального уравнения, удовлетворяющего начальному условию, называется задачей Коши. Практически задачу Коши решают следующим образом: находят общее решение, затем в него подставляют начальные условия, получают систему двух уравнений, определяют произвольные постоянные С₁ и С₂ и  подставляют их конкретные значения в общее решение.

2) ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО

ПОРЯДКА, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА

   Рассмотрим некоторые типы дифференциальных уравнений второго порядка, которые позволяют понизить порядок уравнения и привести его к уравнениям первого порядка.

2.1. Дифференциальное уравнение вида

   Правая часть уравнения не содержит у и у'. Уравнение решается путем последовательного интегрирования. Найдем сначала первую производную (промежуточное общее решение):

   Интегрируя еще раз, получим общее решение:

Пример 1. Найти частное решение уравнения  при заданных начальных условиях у(х=0)=1 и у'(х=0)=1.

Решение. Последовательно интегрируя, найдем сначала первую производную (промежуточное общее решение):

                                                   (2.1)

Интегрируя еще раз, получим общее решение:

                             (2.2)

Так как мы интегрировали дважды, то получили две произвольные постоянные С₁ и С₂. Подставляя начальные условия в соотношения (2.1) и (2.2), получим С₁=1 и С₂=1. Следовательно, частное решение имеет вид:

2.2. Дифференциальное уравнение вида

   Правая часть уравнения не содержит искомой функции у. Уравнение решается с помощью подстановки:  

где z – функция от х. Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка:    .

Решая это уравнение, найдем общее решение в виде  Делая обратную замену  получим еще одно дифференциальное уравнение первого порядка:

 или

Разделяя переменные и интегрируя, получим общее решение

Пример 2. Найти общее решение уравнения  

Решение. Сделаем подстановку:  Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка с разделяющимися переменными:

 или

Разделяем переменные:    Интегрируем:

Получаем промежуточное общее решение:    или

Делая обратную замену  получим еще одно дифференциальное уравнение первого порядка с разделяющимися переменными:    или

Разделяем переменные:

Интегрируя, получим общее решение:

Пример 3. Найти общее решение уравнения  

Решение. Сделаем подстановку:  Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка:

.                                                         (2.3)

   Уравнение (2.3) является однородным и решается с помощью подстановки:

                                               (2.4)

Подставляя (2.4) в (2.3), получим дифференциальное уравнение с разделяющимися переменными:

Сокращаем на х и разделяем переменные:

   Интегрируем:

                                                                    (2.5)

   Интеграл в левой части равенства (2.5) вычисляем методом замены переменной:

После интегрирования (2.5) получаем промежуточное общее решение:

; ;  ;  

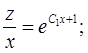
Делая обратную замену  получим дифференциальное уравнение первого порядка с разделяющимися переменными:    или .

Разделяем переменные и интегрируем:        (2.6)

Интеграл, стоящий в правой части, вычисляем с помощью формулы интегрирования по частям:

Тогда

После интегрирования (2.6) получим общее решение: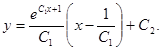   

Пример 4. Найти общее решение уравнения  

Решение. Сделаем подстановку:  Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка:

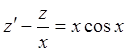       или                     (2.7)

Уравнение (2.7) является линейным неоднородным и решается с помощью подстановки:

                                         (2.8)

Подставляя (2.8) в (2.7), получим:

              (2.9)

Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:

Разделяем переменные и интегрируем:   Получаем:  или       

Функцию подставляем в соотношение (2.9):   

Сокращаем на х, разделяем переменные и интегрируем:   

Находим z:

Делая обратную замену  получим дифференциальное уравнение первого порядка с разделяющимися переменными:  или

Разделяем переменные и интегрируем:

                              (2.10)

Интеграл, стоящий в правой части (2.10), вычисляем с помощью формулы интегрирования по частям:

Тогда

После интегрирования (2.10) получим общее решение: 

2.3. Дифференциальное уравнение вида

   Правая часть уравнения не содержит независимой переменной х. Уравнение решается с помощью подстановки:   или

где z – функция от у, т.е. z= z[y(x)] – сложная функция от х . Тогда:

Исходное уравнение преобразуется в дифференциальное уравнение первого порядка:

где z –  искомая функция, у – независимая переменная.

Решая это уравнение, найдем общее решение в виде  Делая обратную замену  получим еще одно дифференциальное уравнение первого порядка:

 или

Разделяя переменные  и интегрируя, получим общее решение

Пример 5. Найти общее решение уравнения  

Решение. Сделаем подстановку:

Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка с разделяющимися переменными:

Сокращаем на z (z≠0) и  разделяем переменные:

Интегрируем:

Получаем промежуточное общее решение:  или

Делая обратную замену  получим еще одно дифференциальное уравнение первого порядка с разделяющимися переменными:

 или

Разделяем переменные:   Интегрируя, получим общее решение:

3) Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

1.    Линейные однородные дифференциальные уравнения.

Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида   ,                      (1)

т.е. уравнение, которое содержит искомую функцию и её производные только в первой степени и не содержит их произведений. В этом уравнении  и  - некоторые числа, а функция  задана на некотором интервале .

Если  на интервале , то уравнение (1) примет вид    ,       (2)

и называется линейным однородным. В противном случае уравнение (1) называется линейным неоднородным.  Рассмотрим комплексную функцию                  ,                          (3)

где  и  - действительные функции. Если функция (3) является комплексным решением уравнения (2), то и действительная часть , и мнимая часть  решения  в отдельности являются решениями этого же однородного уравнения. Таким образом, всякое комплексное решение уравнения (2) порождает два действительных решения этого уравнения.

Решения однородного линейного уравнения обладают свойствами:

 Если  есть решение уравнения (2), то и функция , где С – произвольная постоянная, также будет решением уравнения (2);

 Если  и  есть решения уравнения (2), то и функция  также будет решением уравнения (2);

 Если  и  есть решения уравнения (2), то их линейная комбинация  также будет решением уравнения (2), где  и  – произвольные постоянные.

Функции  и  называются линейно зависимыми на интервале , если существуют такие числа  и , не равные нулю одновременно, что на этом интервале выполняется равенство

                        .                      (4)

Если равенство (4) имеет место только тогда, когда  и , то функции  и  называются линейно независимыми на интервале .

Пример 1. Функции  и  линейно зависимы, так как на всей числовой прямой. В этом примере .

Пример 2. Функции  и  линейно независимы на любом интервале, т. к. равенство  возможно лишь в случае, когда и ,  и .

2.    Построение общего решения линейного однородного    уравнения.

Для того, чтобы найти общее решение уравнения (2), нужно найти два его линейно независимых решения  и . Линейная комбинация этих решений , где  и  – произвольные постоянные, и даст общее решение линейного однородного уравнения. Линейно независимые решения уравнения (2) будем искать

в виде  ,   (5) ,где   – некоторое число. Тогда , . Подставим эти выражения в уравнение (2):

 или .

Так как , то . Таким образом, функция  будет решением уравнения (2), если  будет удовлетворять уравнению  .                          (6)

Уравнение (6) называется характеристическим уравнением  для уравнения (2). Это уравнение является алгебраическим квадратным уравнением.

Пусть  и  есть корни этого уравнения. Они могут быть или действительными и различными, или комплексными, или действительными и равными. Рассмотрим эти случаи.

 Пусть корни  и  характеристического уравнения действительные и различны. Тогда решениями уравнения (2) будут функции  и . Эти решения линейно независимы, так как равенство  может выполняться лишь тогда, когда и , и . Поэтому общее решение уравнения (2) имеет вид  , где  и  - произвольные постоянные.

Пример 3. Найти общее решение дифференциального уравнения .

Решение. Характеристическим уравнением для данного дифференциального будет . Решив это квадратное уравнение, найдём его корни  и  . Функции  и  являются решениями дифференциального уравнения. Общее решение этого уравнения имеет вид .

 Комплексным числом  называется выражение вида , где  и  - действительные числа, а  называется мнимой единицей. Если , то число  называется чисто мнимым. Если же , то число  отождествляется с действительным числом .

Число называется действительной частью комплексного числа, а - мнимой частью. Если два комплексных числа отличаются друг от друга только знаком мнимой части, то они зазываются сопряжёнными: ,

Пример 4. Решить квадратное уравнение .

Решение. Дискриминант уравнения . Тогда . Аналогично, . Таким образом,  данное квадратное уравнение имеет сопряжённые комплексные корни.

Пусть корни характеристического уравнения комплексные, т.е. , , где .  Решения уравнения (2) можно записать в виде ,  или , .  По формулам Эйлера:   , .

Тогда , . Как известно, если комплексная функция является решением лин. одн. ур-я, то решениями этого уравнения являются и действительная, и мнимая части этой функции. Таким образом, решениями уравнения (2) будут функции  и . Так как равенство

может выполняться только в том случае, если  и , то эти решения линейно независимы. Следовательно, общее решение уравнения (2) имеет вид   ,

где  и  - произвольные постоянные.

Пример 5. Найти общее решение дифференциального уравнения .

Решение. Уравнение   является характеристическим для данного дифференциального. Решим его и получим комплексные корни   , . Функции  и  являются линейно независимыми решениями дифференциального уравнения. Общее решение этого уравнения имеет вид  .

 Пусть корни характеристического уравнения действительные и равные, т.е. . Тогда решениями уравнения (2) являются функции  и . Эти решения линейно независимы, так как выражение  может быть тождественно равным нулю только тогда, когда  и . Следовательно, общее решение уравнения (2) имеет вид .

Пример 6. Найти общее решение дифференциального уравнения .

Решение. Характеристическое уравнение  имеет равные корни . В этом случае линейно независимыми решениями дифференциального уравнения являются функции  и . Общее решение имеет вид .

3.    Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.

Общее решение линейного неоднородного уравнения (1) равно сумме общего решения  соответствующего однородного уравнения и любого частного решения  неоднородного уравнения: .

В некоторых случаях частное решение неоднородного уравнения можно найти довольно просто по виду правой части  уравнения (1). Рассмотрим случаи, когда это возможно.

Пусть неоднородное уравнение имеет вид   ,     (7)

т.е. правая часть неоднородного уравнения является многочленом степени m. Если  не является корнем характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде многочлена степени m, т.е. .

Коэффициенты  определяются в процессе нахождения частного решения.

Если же  является корнем характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде  .

Пример 7. Найти общее решение дифференциального уравнения  .

Решение. Соответствующим однородным уравнением для данного уравнения является

. Его характеристическое уравнение  имеет корни  и .

Общее решение однородного уравнения имеет вид  .

Так как  не является корнем характеристического уравнения, то частное решение неоднородного уравнения будем искать в виде функции . Найдём производные этой функции  ,  и подставим их в данное уравнение :

 или . Приравняем коэффициенты при  и свободные члены: Решив данную систему , получим , . Тогда частное решение неоднородного уравнения имеет вид , а общим решением данного неоднородного уравнения будет сумма общего решения соответствующего однородного уравнения и частного решения неоднородного:

Пусть неоднородное уравнение имеет вид      (8)

Если  не является корнем характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде . Если же  есть корень характеристического уравнения кратности k  (k=1 или k=2), то в этом случае частное решение неоднородного уравнения будет иметь вид .

Пример 8. Найти общее решение дифференциального уравнения .

Решение. Характеристическое уравнение для соответствующего однородного уравнения имеет вид . Его корни , . В этом случае общее решение соответствующего однородного уравнения записывается в виде .

Так как число 3 не является корнем характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде . Найдём производные первого и второго порядков: ,. Подставим в дифференциальное уравнение: +, 

+ , .

Приравняем коэффициенты при  и свободные члены:

 Отсюда , .

Тогда частное решение данного уравнения имеет вид , а общее решение

.