Логарифмические и тригонометрические уравнения смешанного типа профильного уровня.

Уравнения из материалов ЕГЭ профильного уровня смешанного типа.

                    Тригонометрические и показательные уравнения.

1. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

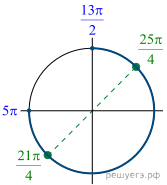Решение. а)  Преобразуем исходное уравнение:

б)  С помощью числовой окружности отберем корни, принадлежащие отрезку Получим числа:

 

Ответ: а) б)

Критерии проверки:

Источник: ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 1.

Классификатор алгебры: Однородные тригонометрические уравнения, Уравнения смешанного типа

Методы алгебры: Сведение к однородному

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, 2.1.5 Показательные уравнения

2.   Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Заметим, что: Далее имеем:

б)  Решая двойное неравенство для каждой из полученных серий корней находим, что заданному промежутку принадлежат числа и только они.

Ответ: а) б)

3. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Запишем уравнение в виде

б)  С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку Получим числа:

 

Ответ: а) б)

4. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Перейдем к одному основанию:

б)  С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку Получим числа:

Ответ: а) б)

5. а)  Решите уравнение:

 

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Перейдем к одному основанию:

 

б)  С помощью числовой окружности отберём корни, принадлежащие отрезку Получим число

 

Ответ: а) б)

6. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Последовательно получаем:

б)  Условию удовлетворяют только числа

 

Ответ: а) б)

7. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащего отрезку

Решение. а)  Запишем исходное уравнение в виде:

Значит, или что невозможно, или откуда или

б)  С помощью числовой окружности отберём корни, принадлежащие отрезку

Получим числа:

 

Ответ: а) б)

8. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. a)  Преобразуем уравнение:

Сделаем замену переменной тогда уравнение примет вид:

Второй корень является посторонним. Таким образом,

 

б)  При помощи единичной окружности отберем корни удовлетворяющие промежутку В него попадают

 

Ответ: а) б)

9. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. a)  Преобразуем уравнение:

б)  При помощи единичной окружности отберём корни, лежащие на отрезке Получаем число

 

Ответ: а) б)

 

 

10. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. a)  Преобразуем исходное уравнение:

Сделаем замену и решим полученное уравнение:

Вернёмся к исходной переменной:

 

б)  Произведем отбор корней при помощи единичной окружности (см. рис.) Подходят корни

Ответ: а) б)

11. Решите уравнение

б)  Найдите корни этого уравнения, по абсолютной величине не превышающие

Решение. а)  Заметим, что

Тогда

 

 

б)  Отберём корни, по абсолютной величине не превышающие т. е. корни, лежащие на промежутке с помощью тригонометрической окружности (см. рис.). Получаем:

 

 

Ответ: а) б)

12. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Дробь равна нулю, если ее числитель равен нулю, а знаменатель существует. Поэтому при условии имеем:

С учетом ограничения

б)  Отберём корни на промежутке с помощью тригонометрической окружности (см. рис.), получим

 

Ответ: а) б)

13. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Сделаем замену и преобразуем уравнение

 

Вернёмся к исходной переменной:

б)   Корни уравнения, принадлежащие отрезку отберём с помощью единичной окружности. Заметим, что тогда а Подходит только корень

 

Ответ: a) б)

14. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие промежутку

Решение. а)  На области определения квадратного корня справедливо равенство Поэтому при условии

правая часть уравнения равна 3. Получаем:

Оба корня удовлетворяют условию (⁎). Итак, x = 0, x = −1.

б)  Заметим, что следовательно, На отрезке лежит число −1.

 

Ответ: а) б) −1.

15. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Преобразуем уравнение:

Решим уравнение (⁎):

Все найденные корни удовлетворяют условию

б)  Отберём корни при помощи единичной окружности (см. рис.). Подходят числа

 

Ответ: а) б)

16. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Упростим показатель степени в правой части уравнения, для этого применим формулу косинуса разности:

Преобразуем исходное уравнение к квадратному относительно показательной функции:

б)  Отберём корни при помощи единичной окружности. Подходят

 

Ответ: а) б)

17. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Дробь равна нулю в случае, когда числитель равен нулю, а знаменатель отличен от нуля. Поэтому исходное уравнение равносильно системе

б)  Заметим, что поэтому найденный корень лежит на заданном отрезке.

 

Ответ: а) б)

18. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Преобразуем уравнение:

б)  Отберём корни при помощи единичной окружности. Подходят

 

Ответ: а) б)

19. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  При условии исходное уравнение эквивалентно уравнению:

Условию удовлетворяет только

б)  Отберём корни при помощи тригонометрической окружности. Подходит

 

Ответ: а) б)

20. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Применим формулу приведения, сведем уравнение к квадратному относительно косинуса:

б)  Отберём корни при помощи тригонометрической окружности. Подходят

 

Ответ: а) б)

21. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Преобразуем показатель степени в правой части уравнения, используя формулу косинуса разности:

Тогда правая часть принимает вид

Положим получим:

Возвращаясь к исходной переменной, получаем:

б)  Для отбора корней воспользуемся тригонометрической окружностью. Подходят:

 

Ответ: а) б)

22. а)  Решите уравнение

б)  Найдите все корни уравнения, принадлежащие отрезку

Решение. a)  Пусть тогда

Вернёмся к исходной переменной:

б)  Отберём корни, принадлежащие отрезку с помощью двойного неравенства:

Тогда,

 

Ответ: а) б)

23. а)  Решите уравнение

б)  Найдите все корни уравнения, принадлежащие отрезку

Решение. а)  Знаменатель дроби должен быть отличен от нуля, то есть

При этом условии числитель дроби должен быть равен нулю. Применим формулы и получим:

Если и угол х лежит в первой четверти, то а тогда что обращает знаменатель в нуль. Если же и угол х лежит во второй четверти, то а тогда что допустимо. Следовательно, решением уравнения является серия

б)  Отберем корни, решая двойное неравенство:

Акрсинус положительного числа лежит в интервале поэтому левая часть двойного неравенства больше  –5π, а правая  — меньше –4,5π. Следовательно, число 2πk лежит в интервале (–5π; –4,5π), а значит, Найденному значению параметра соответствует корень

 

Ответ: а) б)

 

24.

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Решим уравнение:

Пусть тогда

Вернёмся к исходной переменной:

б)  С помощью единичной окружности отберём корни на отрезке Находим:

 

Ответ: а) б)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                           

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                   Решить самостоятельно.

1. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

2. а)  Решите уравнение          

б)  Найдите все корни этого уравнения, принадлежащие отрезку

3. а)  Решите уравнение

б)  Найдите все его корни, принадлежащие отрезку

4. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

5. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

 

6. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

7. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

8. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

9. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

10 а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы.

 

1. а) б) (№5)

 

2.: а) б) (№6)

 

3. а) б) (№12)

4. : а) б)  (№23)

5. а) б)   (№28)

6. : а) б)     (№42)

7. а) б)     )№45)

8. а) б)    (№61)

9. а) б) и      (№65)

10. : а) б)    (№77)

 

 

 

 

 

 

Скачано с www.znanio.ru