Поделиться
Логические задачи 2013.pdf
О. Б. Богомолова
ЛОГИЧЕСКИЕ ЗАДАЧИ
4-е издание, исправленное и дополненное
Москва
БИНОМ. Лаборатория знаний
удк 004.9
ББК 32.97
Б74
Богомолова О. Б.
Б74 Логические задачи / О. Б. Богомолова. — 4-е изд., испр. и доп. — М. : БИНОМ. Лаборатория знаний, 2013.— 277 с. : ил.
rsBN 9786-9963-1001-2
Предлагается система логических задач для школьников разного возраста. Задачи структурированы по смысловому содержанию и приемам решения, Даны подробные схемы решения задач разных типов.
Книга способствует развитию логического мышления, учит правильно строить рассуждения, выдвигать и исследовать гипотезы, самостоятельно принимать решения.
Для школьников 6—11 классов, учителей и методистов. удк 004.9 БЫС 32.97
Учебное изДание
Богомолова Ольга Борисовна
ЛОГИЧЕСКИЕ ЗАДАЧИ
Ведущие редакторы О. А. Полежаева, Д. Ю. Усенков Художник Н. А. Новак
Технический редактор Е. В. Денюњова. Корректор Е. Н. Клитина Компьютерная верстка: Л. В. Катуркина
Подписано в печать 06.11.12. Формат 60х 90/16. Усл. печ. л. 17,5. Тираж 2000 экз. Заказ 1703.
Издательство «БИНОМ. Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. З
Телефон: (499) 157-5272 e-mail: binom@Lbz.ru http://www.Lbz.ru, http://metodist.Lbz.ru
Отпечатано в ООО ПФ «Полиграфист» ,
160001, г. Вологда, ул. Челюскинцев, З.
БИНОМ. Лаборатория rsBN
978-5-9963-1001-2 знаний, 2013
Введение
Перед учителем в настоящее время стоит задача не столько вооружить учащихся прочными знаниями, сколько научить их учиться самостоятельно.
Умение мыслить последовательно, рассуждать доказательно, строить гипотезы, опровергать неправильные выводы не приходит само по себе. Это умение развивает наука логика.
Систематическое овладение азами этой науки невозможно без решения логических задач. И начинать обучение учащихся основам решения таких задач необходимо с самого раннего возраста, с начальной школы.
Задача учителя — привить своим ученикам привычку к упорному, самостоятельному, творческому труду, выработать у них умение преодолевать трудности при решении задач и вообще при любой работе, связанной с учебной деятельностью. Всем известно: дети любят учиться, но при этом забывается, что дети любят хорошо учиться. И одним из мощных рычагов воспитания трудолюбия, желания и умения хорошо учиться является создание условий, обеспечивающих ребенку успех в учебной программе, на пути от незнания к знанию, от неумения к умению. К таким условиям, безусловно, можно отнести процесс решения нестандартных, логических задач.
Решение задач — это практическое искусство; подобно плаванию, катанию на лыжах или игре на фортепиано, научиться ему можно, только подражая хорошим образцам и постоянно практикуясь. Мышление, как учит психология, начинается там, где нужно решить ту или иную задачу. При этом каждая задача неизменно заканчивается вопросом, на который надо дать ответ. Задача пробуждает мысль учащегося, активизирует его мыслительную деятельность. Решение задач по справедливости считается гимнастикой для ума.
Введение
В данном пособии предлагается набор логических задач, классифицированных по смысловому содержанию и логическим приемам решения. 1. Задачи с отношениями (решение нескольких задач рассмотрено очень подробно).
2. Задачи с использованием схем и таблиц.
З. Задачи на переправу.
4. Задачи, решаемые с помощью графов.
5. Задачи на перебор возможных вариантов.
6. Занимательные задачи.
7. Набор заданий для устной работы.
В каждой задаче представлены: о краткая запись;
• запись схемы — модели условия задачи;
• рассуждения к решению задачи;
• выводы, сделанные из этих рассуждений.
Как правило, при решении задачи могут быть выделены следующие этапы.
1. Анализ условия задачи (выделение исходных данных).
2, Поиск метода решения. З. Символическая запись задачи.
4. Рассуждения и пояснения к решению.
5. Анализ полученных результатов и запись ответа.
Условия логических задач лучше наглядно представлять в виде чертежей, рисунков, схем. Это облегчает решение задач, делает его более убедительным и доказательным.
В данной книге рассмотрены возможные приемы, направленные на развитие логического мышления на разных ступенях обучения детей решению задач.
В мыслительной деятельности учащегося при решении задачи анализ и синтез занимают столь большое место, играют настолько большую роль, что в методике им приписывается даже значение метода решения. Анализ и синтез проходят через весь процесс решения
задачи. Сначала учащийся анализирует конкретное содержание задачи: о чем в ней говорится, о каких фактах или явлениях, в какой последовательности они происходят. Читая и перечитывая условие, учащийся выделяет из него данные, старается уловить взаимосвязи, которые существуют между данными в задаче.
Читая вопрос задачи, учащийся сосредоточивает на нем особое внимание, стараясь отчетливее и глубже понять, что спрашивается в задаче или, иначе говоря, в чем именно заключается задача. На этом первом этапе знакомства с задачей преобладает аналитическая деятельность.
Чтобы облегчить анализ условия задачи, учитель прибегает к его конкретизации путем использования той или иной формы наглядности — рисунка, чертежа, схемы, применения того или иного предметного наглядного пособия.
При работе над вопросом задачи главное и наиболее трудное для ученика — определить, в какой связи эта искомая величина находится с заданными исходными величинами.
В простой задаче ответ на последний вопрос вытекает сам собой из предыдущего анализа. Но в сложной задаче незнакомого для ученика типа для ответа на этот вопрос может потребоваться ряд рассуждений, в каждом из которых выражается зависимость одного условия от другого. Рассуждения должны представлять собой стройную логическую цепь суждений, в которой каждое предыдущее суждение является основой для последующего и с необходимостью вытекает из предыдущего.
В результате такой мыслительной деятельности сложная, составная задача распадается на ряд простых, решение которых приводит к ответу на вопрос основной задачи. При этом простые задачи располагаются в определенной последовательности, которая устанавливается планом решения, требуя от ученика формулировать вопросы точно, ясно, кратко. На этом этапе решения на первый план выступает синтетическая деятельность.
Введение
Затем начинается собственно решение задачи. В этом процессе анализ и синтез тесно переплетаются между собой. Поставив вопрос, ученик отбирает из задачи условия, которые необходимы для ответа на этот вопрос. И так — до ответа на последний вопрос.
Из сказанного видно, какую большую роль играют при решении задачи такие приемы логического мышления, как синтез и анализ, конкретизация, абстрагирование, а также умения рассуждать связно и последовательно, формулировать вопросы точно и однозначно.
Назначение логических задач и упражнений
состоит в активизации умственной деятельности ребят, в оживлении процесса
обучения. Применяются они как на занятиях, так и в повседневной жизни.
Раздел 1. Задачи с отношениями
В данном
разделе представлены логические задачи с транзитивными отношениями: «больше» ,
«меньше», «равно» и другими.
Необходимым условием успешного решения таких задач является умение перейти от отношений разного вида между элементами задачи к отношениям одного вида. Например, если в задаче встречаются отношения «легче» и «тяжелее», то надо заменить отношение «легче» отношением «тяжелее» с соответствующей перестановкой исходных данных.
 |
Следует учитывать, что некоторые ученики плохо воспринимают задачи на слух, поэтому учителю нужно проговаривать условие задачи, выделяя голосом слова, показывающие, что происходит с предметом, о котором говорится в условии. После чтения текста задачи начинается работа над усвоением содержания с одновременной его краткой записью. Такая работа над условием помогает детям избежать возможных ошибок в рассуждениях.
Для учащихся 2—5 классов.
1 .1 . ЗАДАЧИ С ТРАНЗИТИВНЫМИ ОТНОШЕНИЯМИ Задача 1. Что тяжелее всего?
Груша тяжелее яблока, а персик легче яблока. Какой из фруктов самый тяжелый?
Решение
Ученики проговаривают условие задачи и записывают его в тетрадь.
Даны фрукты: яблоко, груша, персик. Обозначим их символьными переменными Я, Г, П соответственно и запишем эти данные в раздел «Дано: » .
В задаче требуется узнать, какой из фруктов самый тяжелый. Запишем этот вопрос в раздел «Надо: ».
|
Дано: Яблоко (Я) Груша (Г) Персик (П) |
|
Надо: Что тяжелее всего? |
Рассуждения:
После слова «Дано:» записываются все элементы задачи, причем для каждого из них вводится обозначение символьная переменная. Проводится горизонтальная черта, под которой пишется слово «Надо:» и вопрос задачи. Затем проводится вертикальная черта, отделяющая условие и вопрос от рассуждений (решения).
В разделе «Рассуждения: » строится схема — модель условия задачи, в которой заданные в условии задачи отношения записываются с помощью символьных переменных.
Например, для нашей задачи мы акцентируем внимание на отношении «тяжелее». Тогда первое отношение — «груша тяжелее яблока» будет записано так: ГЯ.
Второе отношение «персик легче яблока» надо перевести в равнозначное отношение, выраженное словом «тяжелее» . Получим: «яблоко тяжелее персика» — ЯП.
Запишем условие задачи с отношением «тяжелее» в одной строке: ГЯЯП.
В данной записи выделим (обведем рамкой) одинаковые символьные переменные и запишем новое отношение с одной переменной вместо выделенных двух: гяп.
Расставим под переменными цифры, обозначающие порядок, соответствующий отношению «тяжелее» : меньшая цифра обозначает более тяжелый предмет.
Полученная запись символизирует отношение «тяжелее» между данными задачи.
с отношениями
Рассуждения ученика:
• Будем записывать решение в одной строке, используя символьные переменные.
о Так как (по условию задачи) груша тяжелее яблока, запишем: ГЯ.
• Так как (по условию задачи) персик легче яблока, яблоко тяжелее персика. Запишем соответственно: яп.
• Выделим прямоугольником две одинаковые символьные переменные.
• Теперь можно ответить на вопрос задачи: тяжелее всех груша.
Эталон записи решения задачи в тетради:
|
Дано: Яблоко (Я) Груша (Г) Персик (П) |
|
Надо: Что тяжелее всех? |
Рассуждения:
г яп
Ответ: груша тяжелее всех фруктов.
Задача 2. Что толще всего?
Ствол дуба толще, чем ствол сосны, а ствол сосны толще, чем ствол березы. Ствол какого дерева самый толстый?
Ответ: ствол дуба самый толстый.
Задача З. Что дороже всего?
Ручка дороже тетради, карандаш дешевле тетради. Что дороже всего?
Ответ: ручка дороже всех предметов.
Задача 4. На что идет больше всего ткани?
На халат идет больше ткани, чем на платье. На рубашку — меньше, чем на платье. На что идет больше ткани — на рубашку или на халат?
Ответ: больше ткани идет на халат.
Задача 5. Кто старше всех?
Три брата — Ваня, Саша, Коля — учатся в разных классах одной школы. Коля старше Вани, а Саша моложе Вани. Назовите имена старшего, среднего и младшего братьев.
Ответ: Коля старший брат, Ваня средний, Саша — младший.
Задача 6. Кто выше?
Назовите имена самого высокого, среднего и самого низкого мальчиков, если Толя выше Коли, а Вася ниже Коли.
Ответ: Толя самый высокий, Коля — среднего роста, Вася ниже всех.
Задача 7. Цветные карандаши
У Пети три карандаша желтый, коричневый и черный. Назовите самый короткий и самый длинный карандаши, если известно, что:
а) желтый карандаш короче коричневого, а черный — короче желтого;
б) желтый карандаш длиннее черного, а коричневый короче черного.
Ответ: а) коричневый карандаш — самый длинный, черный — самый короткий;
б) желтый карандаш — самый длинный, коричневый — самый короткий.
1.2. ЗАДАЧИ С НЕКОРРЕКТНЫМИ УСЛОВИЯМИ
После отработки
решений задач с различными транзитивными отношениями целесообразно предложить
учащимся задачи с некорректными условиями, когда данных недостаточно, имеет
место их излишек или несоответствие. Эти задачи помогут приучить детей к
сознательному, правильному чтению условия задачи и анализу ее исходных данных.
Задача 8. Кто живет выше всех?
Ваня живет выше Сережи, а Сережа — ниже Наташи. Кто живет выше: Наташа или Ваня?
с отношениями
Решение
Эталон записи решения задачи в тетради:
|
Дано: Ваня (В) Наташа (Н) Сережа (С) |
|
Надо: Кто живет выше всех? |
Рассуждения:
вснс
Ответ: нельзя ответить на вопрос задачи — недостаточно исходных данных.
Задача 9. Рыбалка
Рыбак поймал окуня, ерша и щуку. Щуку он поймал раньше, чем окуня, а ерша — позже, чем щуку. Можно ли сказать, какая рыба поймана раньше: окунь или ерш?
Ответ: нельзя ответить на вопрос задачи — недостаточно исходных данных.
Задача 10. Футбольные мячи
Среди трех футбольных мячей красный мяч тяжелее коричневого, а зеленый легче красного. Какой мяч тяжелее: коричневый или зеленый?
Ответ: нельзя ответить на вопрос задачи — недостаточно исходных данных.
Задача 11. Три товарища
В одном классе учатся три товарища Сережа, Толя, Юра. По росту они немного отличаются друг от друга, поэтому на уроке физкультуры в шеренге они стоят подряд по росту. Сережа не ниже Толи, Юра не выше Толи, Сережа выше Юры. Кто из них ниже всех, средний по росту и выше всех?
Ответ: нельзя ответить на вопрос задачи, так как ребята могут быть одного роста («не ниже», «не выше»); избыток условий.
Задача 12. Веселые девочки
Галя веселее Оли, а Оля не веселее Гали. Кто из них веселее?
Ответ: нельзя ответить на вопрос
задачи 
противоречие в условиях.
Задача 13. Темные волосы
У Кати волосы темнее, чем у Зины. У Зины волосы тоньше, чем у Ани. У кого волосы темнее всех?
Ответ: нельзя ответить на вопрос задачи — несоответствие условий.
1 „З. ЗАДАЧИ С ОТНОШЕНИЕМ РАВЕНСТВА
В задачах с отношением равенства некоторые данные приравниваются к другим.
Задача 14. Кто ниже всех?
Винни-Пух такого же роста, как Крокодил Гена, а Крокодил Гена выше Чебурашки. Кто ниже всех?
Решение
Сначала ученики проговаривают условие задачи и записывают его в тетрадь,
Даны персонажи — Винни-Пух, Крокодил Гена, Чебурашка. Обозначим их символьными переменными В, К, Ч соответственно. Запишем эти данные в раздел
«Дано: » .
В задаче требуется узнать, кто ниже всех. Запишем этот вопрос в раздел «Надо: ».
|
Дано: Винни-Пух (В) Крокодил Гена (Г) Чебурашка (Ч) |
|
Надо: Кто ниже всех? |
Рассуждения:
Рассуждения ученика:
• Запишем решение на одной строке, используя символьные переменные.
• Так как (по условию задачи) Винни-Пух и Крокодил Гена одного роста, поставим знак равенства между символьными переменными: В = К.
о Так как (по условию задачи) Крокодил Гена выше Чебурашки, запишем: КЧ.
о Выделим прямоугольником две одинаковые символьные переменные.
• Теперь можно дать ответ на вопрос задачи: Чебурашка ниже Крокодила Гены и Винни-Пуха. Эталон записи решения задачи в тетради:
|
Дано: Винни-Пух (В) Крокодил Гена (Г) Чебурашка (Ч) |
|
Надо: Кто ниже всех? |
Рассуждения:
 |
Задача 15. Кто моложе всех?
На прием к доктору Айболиту пришли филин, щука и цапля. Доктор записал в карточку возраст каждого больного. Оказалось, что щука такого же возраста, как и филин, а цапля моложе филина. Кто старше: цапля или щука? Кто моложе всех?
Ответ: щука старше цапли; цапля моложе всех.
Задача 16. Что толще всего?
Синий карандаш толще красного, а красный такой же по толщине, как и голубой. Какой карандаш толще всех?
Ответ: синий карандаш.
Задача 17. Кто выше?
Ваня и Саша одного роста. Саша и Митя тоже одного роста. Кто выше: Митя или Ваня?
Ответ: все мальчики одного роста.
Задача 18. Что тяжелее?
Арбуз и кочан капусты имеют одинаковый вес. Кочан капусты весит столько же, сколько одна тыква. Что тяжелее: арбуз или тыква?
Ответ: арбуз и тыква весят одинаково.
Задача 19. Кто старше?
Лена и Тамара одного возраста. Тамара и
Маша 
одногодки. Кто старше: Лена или Маша?
Ответ: Лена и Маша одного возраста.
1-4. ЗАДАЧИ С НЕТРАНЗИТИВНЫМИ ОТНОШЕНИЯМИ
В задачах данного типа из-за нетранзитивности отношений для того, чтобы сделать вывод, необходимы дополнительные условия (ограничения).
Задача 20. Музыкальные инструменты
Два мальчика играют на гитарах, а один — на балалайке. На чем играет Юра, если Миша с Петей играют на разных инструментах и Петя с Юрой — тоже?
 |
Даны имена мальчиков: Юра, Миша, Петя. Обозначим их символьными переменными Ю, М, П соответственно (прописные буквы). Даны инструменты, на которых играют мальчики: две гитары и одна балалайка. Обозначим названия инструментов переменными г и б (строчные буквы). Запишем эти данные в раздел «Дано: » .
В задаче требуется узнать, на каком инструменте играет Юра. Запишем этот вопрос в раздел «Надо: ».
Дано: Рассуждения: юра (Ю) Миша (М) Петя (П) гитары (г) балалайка (б) Надо:
На чем играет Юра?
Рассуждения ученика:
• Выделим повторяющуюся в условии задачи переменную. Она соответствует имени Петя. Запишем две одинаковые символьные переменные друг под другом.
• Так как (по условию задачи) Миша и Петя играют на разных инструментах, над символьной переменной П запишем М. Так как (по условию задачи) Петя с Юрой тоже играют на разных инструментах, под символьной переменной П запишем Ю.
• Выделим прямоугольником две одинаковые символы ные переменные.
• Запишем справа и слева переменные, которыми обозначены названия инструментов, и в скобках числа — количества инструментов.
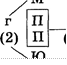
• Так как (по условию) балалайка одна, на ней играет Петя. Следовательно, Миша и Юра играют на гитарах. Тем самым получен ответ на вопрос задачи.
 |
|
Дано: юра (Ю) Миша (М) Петя (П) гитары (г) балалайка (б) |
|
Надо: На чем играет Юра? |
Рассуждения:
м б
(1)
Ответ: Юра играет на гитаре.
Задача 21. Семья
В семье трое детей — два мальчика и одна
девочка. 
Их имена начинаются с букв «А», «В», «Г».
Имена, начинающиеся с букв «А» и «В», это имена одного мальчика и одной
девочки. Имена, начинающиеся с букв «В» и «Г», — это имена одного мальчика и
одной девочки. С какой буквы начинается имя девочки?
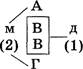
Решение
Эталон записи решения задачи в тетрадь:
|
Дано: в мальчики (м) девочка (д) |
|
Надо: С какой буквы начинается имя девочки? |
Рассуждения:
Ответ: имя девочки начинается с буквы «В».
Задача 22. Сестры
У трех сестер — Юли, Тони и Веры — два платка синего цвета и один — розового. Какого цвета платок у каждой из них, если у Юли и Тони платки разного цвета, а у Веры и Юли — тоже?
 |
синие.
Задача 23. Вышивка
Галя, Маша, Даша и Лена вышивали, Три девочки вышивали листочки, а одна девочка — цветочки. Маша и Галя вышивали разное, Галя и Лена — тоже. Что вышивала каждая девочка?
Решение
|
Дано: Галя (Г) Маша (М) Даша (Д) Лена (Л) листочки (л) цветочки (ц) |
|
Найти: Кто что вышивал? |
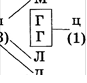Эталон записи решения задачи в тетради: Рассуждения: м
л
(3)
Ответ: Галя вышивала цветочки; Маша, Даша и
Лена — листочки.
Задача 24. Варенье
Оля, Таня, Юля и Ира варили варенье. Две девочки
варили варенье из смородины, две другие
— из крыжовника. Таня и Ира варили из разных ягод, Ира и Оля 
тоже. Ира
варила варенье из крыжовника. Какое варенье варила каждая девочка?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Оля (О) Таня (Т) юля (Ю) ира (И) смородина (с) крыжовник (к) |
|
Найти: Какое варенье варила каждая девочка? |
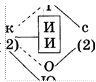Рассуждения:
ю
 |
Оля и Таня — из смородины.
Задача 25. Рыбалка
Дима, Миша и Леша ловили рыбу. Каждый из них поймал щуку или окуня. Кто что поймал, если Дима и Миша поймали одинаковых рыб, Дима и Леша — разных, Леша поймал щуку?
Решение
Эталон записи решения задачи в тетради:
Дано: Рассуждения:
|
(Д) (М) (Л) (щ) унь (о) |
|
какую рыбу поймал? |
|
д д |
|
Дима м
Миша Леша щука щ ок л
Найти:
Кто
Ответ: Миша и Дима поймали окуней, Леша
щуку.
Задача 26. Фрукты
Нина, Валя, Инна, Марина и Костя собирали фрукты. Трое ребят собирали яблоки, двое — груши. Костя и Марина собирали одинаковые фрукты, Марина и Валя разные. Что собирал каждый из ребят, если Валя и Нина собирали разные фрукты?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Нина (Н) Валя (В) Инна (И) Марина (М) Костя (К) яблоки (я) груши (г) |
|
Найти: Что собирал каждый из ребят? |
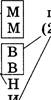Рассуждения:
 |
н и
Ответ: Костя, Марина и Нина собирали яблоки; Валя и Инна — груши.
Задача 27. Рисование
Света, Зина, Галя, Таня рисовали цветы. Одна рисовала красным карандашом, трое других синими. Галя и Зина рисовали карандашами разного цвета, Зина и Таня — тоже. Двое из них рисовали васильки, а другие колокольчики. Кто что рисовал, если Зина и Таня рисовали одинаковые цветы, а Зина рисовала василек?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Света (С) Зина (З) Галя (Г) Таня (Т) василек (в) колокольчик (к) красный (кр) синий (син) |
|
Найти: Кто что рисовал и каким цветом? |
 |
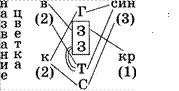Рассуждения:
Ответ: Света и Галя рисовали колокольчик синими карандашами, Зина — василек красным карандашом, Таня — василек синим карандашом.
Задача 28. Фигурки из пластилина
Юра, Гена, Саша и Толя лепили зверей из пластилина. Двое лепили из серого пластилина, двое — из черного. Саша и Гена лепили из пластилина разного цвета, Гена и Толя — тоже. Юра лепил из черного пластилина, как и Гена. Получились трое мишек и один зайчик.
Гена лепил не мишку. Кто кого лепил и какого цвета получились животные?
Решение
|
Дано: юра (Ю) Гена (Г) Саша (С) Толя (Т) мишка (м) зайчик (з) серый (сер) черный (ч) |
|
Найти: Кто что лепил и пластилином какого цвета? |
Эталон записи решения задачи в тетради:
Рассуждения:
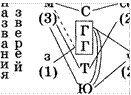п н сер л (2) а
в т е и ч т л и
(2) н
а
Ответ: Толя и Саша мишку,
Гена
лепили серого черного зайчика, Юра — черного мишку.
 |
У Марины, Кати, Сони,
Лизы и Ларисы живут три кошки и две собаки. Кто у какой девочки живет, если у
Сони и Лизы одинаковые животные, у Кати и Сони тоже, у Сони и Ларисы разные
животные?
Решение
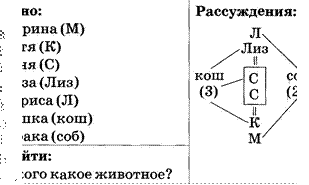Эталон записи решения
задачи в тетради: Дано:
Ответ: у Ларисы и Марины собаки, а у Кати,
Сони и Лизы — кошки.
1.5. ЗАДАЧИ С НЕСКОЛЬКИМИ ОТНОШЕНИЯМИ
Рассматриваемые
составные задачи состоят из нескольких простых. Схема-модель для таких задач
строится следующим образом:
е все отношения записываются символически; о отношения предлагается записывать в несколько строк (не более трех отношений на одной строке);
• кружком выделяются символьные переменные, которые не повторяются дважды; одна из них является началом ответа, а другая — концом;
• последовательно попарно обводятся одинаковые символьные переменные; е все отношения записываются последовательно в одну строку, проставляется порядок и даются ответы на поставленные вопросы.
Задача 30. Кто после кого пришел?
 |
Решение
Рассуждения ученика:
• Так как (по условию) лиса пришла раньше медведя, запишем: ЛМ.
• Так как (по условию) волк пришел позже зайца, заяц пришел раньше волка. Запишем: ЗВ.
• Так как (по условию) медведь пришел раньше зайца, запишем: МЗ.
• Так как (по условию) сорока пришла позже волка, волк пришел раньше сороки. Запишем: ВС.
• Выделим кружком символьные переменные, которые не повторяются дважды. Это Л и С. Теперь мы можем сказать, что лиса пришла первой (буква Л стоит на первом месте в соответствующей паре букв), а сорока — последней (буква С стоит второй в соответствующей паре).
е Обведем попарно
одинаковые символьные переменные в следующем порядке. Сначала обводятся
переменные М (М стоит справа от первого кружка Л 
медведь пришел после
лисы). Затем обводятся переменные З (З стоит справа от М — заяц пришел вслед за
медведем).
о Теперь можно записать все условия в
одну строку и проставить порядок. Получим ответ на вопрос задачи: лиса пришла
первой, медведь — вторым, заяц 
третьим, волк — четвертым, сорока — пятой.
Эталон записи решения задачи в тетради:
|
Дано: Лиса (Л) Волк (В) Заяц (З) Медведь (М) Сорока (С) |
|
Надо: Кто после кого пришел в гости? |
 |
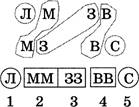Рассуждения:
Ответ: лиса пришла раньше всех, медведь пришел вторым, заяц третьим, волк четвертым, сорока — пятой.
Задача 31. Очередь
Митя, Сережа, Толя, Юра и Костя пришли в музей до открытия и встали в очередь. Митя пришел позже Сережи, Толя раньше Кости, Митя раньше Толи, юра— позже Кости. В каком порядке ребята стояли в очереди?
Ответ: порядок ребят в очереди: Сережа, Митя, толя, костя, юра.
Задача 32. Концерт
Дети приготовили номера выступлений для концерта: фокусы, частушки, танец, песню, стихотворение. На концерте стихи прочли перед танцем, фокусы показывали после частушек, танец исполняли перед песней, частушки пропели после песни. В какой последовательности проходили выступления?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Фокусы (Ф) Частушки (Ч) Танец (Т) Песня (П) Стихотворение (С) |
|
Найти: В какой последовательности проходили выступления? |
Рассуждения:
1
Ответ: стихотворение, танец, песня, частушки, фокусы.
Задача 33. Скачки
 |
Решение
|
Дано: Цыган (Ц) Зорька (З) Скрипка (С) Калитка (К) Траид (Т) |
|
Найти: В какой поёледовательности бежали лошади? |
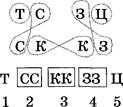Эталон
записи решения задачи в тетради: Рассуждения:
1 5
Ответ: Траид, Скрипка, Калитка, Зорька, Цыган.
Задача 34. Звери
Лисичка пригласила собирать грибы волка, зайца, оленя, мышь и бурундука. Кто больше всех собрал грибов, если мышь собрала не меньше грибов, чем заяц, лиса меньше, чем волк, бурундук больше, чем олень, лиса — больше, чем мышь, бурундук — не больше, чем заяц?
Ответ: больше всех грибов собрал волк.
Задача 35. Стоянка машин
 |
«Волга», «Мерседес», «Тойота», «Ауди».
Задача 36. Урок физкультуры
На уроке физкультуры учитель выстроил девочек 
Свету, Галю, Нину, Олю и Арину — в шеренгу по росту. Известно, что Света выше Нины, Оля не выше Арины, Нина выше Арины, Галя ниже Оли. В каком порядке стоят девочки?
Ответ: Света, Нина, Арина, Оля, Галя.
Задача 37. Деревья
Возле почты растут шесть деревьев: сосна, береза, липа, тополь, ель и клен. Известно, что береза ниже тополя, липа выше клена, сосна ниже ели, липа ниже березы, сосна выше тополя. Укажите, как располагаются деревья по высоте.
Решение
Эталон записи решения задачи в тетради:
|
Дано: Сосна (С) Береза (Б) Липа (Л) Тополь (Т) Ель (Е) Клен (К) |
|
Найти: Как располагаются деревья по высоте? |
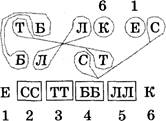Рассуждения:
Ответ: самое высокое дерево — ель, далее идут сосна, тополь, береза, липа, клен.
Задача 38. Животные
 |
Решение
Эталон записи решения задачи в тетради:
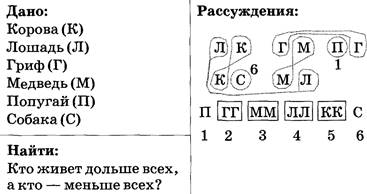
Ответ: дольше всех живет попугай,
меньше всех 
собака.
Задача 39. Растения
Известно, что каждое дерево может прожить определенное количество времени. Какое из деревьев является «долгожителем», если липа живет меньше ели, секвойя — дольше дуба, кипарис дольше секвойи, береза — не дольше груши, липа дольше груши, дуб — не меньше ели?
Ответ: дольше всех живет кипарис.
1.6. ЗАДАЧИ НА СРАВНЕНИЕ ЭЛЕМЕНТОВ В ОТНОШЕНИЯХ
Сопоставление,
или сравнение, это логический прием, с помощью которого устанавливаются
сходство или различия объектов. Результат сравнения обозначается с помощью
терминов «равно», «больше» , «меньше» в зависимости от отношения сравниваемого
объекта к другому объекту, с которым его сравнивают.
 |
Задача 40, Что тяжелее?
Батон хлеба и пачка сахара весят больше, чем батон и коробка конфет. Что весит больше: сахар или конфеты?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Батон (Б) Сахар (С) Конфеты (К) |
|
Надо: Что весит больше: сахар или конфеты? |
Рассуждения:
СБ БК.
Одинаковый компонент обеих частей неравенства — Б. Сократим обе части неравенства на этот компонент. Получим:
Ответ: сахар весит больше, чем конфеты.
Задача 41. Что дороже?
За пакет муки, пачку сахара и пачку кофе заплатили больше, чем за такой же пакет муки, пачку сахара и булку. Что дороже: кофе или булка? Ответ: кофе дороже булки.
Задача 42. Картофель
На одной чаше весов лежат три одинаковых
пакета с картофелем и две гири по 2 кг каждая, а на другой 
четыре таких
же пакета с картофелем и 1 гиря в 1 кг. Сколько весит пакет с картофелем, если
весы находятся в равновесии?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Пакет (П) Гири: 2 кг, 2 кг, 1 кг |
|
Надо: Сколько весит пакет? |
Рассуждения:
3П+2+2=4П+1.
Одинаковый компонент обеих частей равенства:
 |
(сократим обе части равенства). Получим: 2+1-п п=з.
Ответ: пакет картофеля весит З кг.
Задача 43. Фрукты
На одной чаше весов лежат шесть одинаковых яблок и три одинаковые груши, на другой — три таких же яблока и пять таких же груш. Весы находятся в равновесии. Что легче: яблоко или груша? Ответ: яблоко легче груши.
Задача 44. Овощи
На одной чаше весов лежат два одинаковых кочана капусты и три гири по 2 кг, а на другой — четыре таких же кочана капусты. Сколько весит кочан капусты, если весы находятся в равновесии?
Ответ: кочан капусты весит З кг.
Задача 45. Кошки и котята
На чашечных весах взвесили четырех кошек и трех котят, их вес оказался равным 15 кг. Затем взвесили трех кошек и четырех котят, их вес составил 13 кг. Найти вес одной кошки и одного котенка, считая вес всех кошек одинаковым и вес всех котят также одинаковым.
Решение
Эталон записи решения задачи в тетради:
|
Дано: Кошка (К) Котенок (Кт) |
|
Надо: Сколько весит котенок и сколько кошка? |
Рассуждения:
+ зкт -15, (1) ЗК + =13. (2)
Вычтем (2) из ( 1). Получим:
к = кт +2. (3)
 |
13,
(4)
Подставим выражение для Кт из (4) в (З). Получим:
к=з.
Ответ: кошка весит З кг, котенок — 1 кг.
Задача 46. Вес раковины
На чашечных весах три кубика и морская раковина уравновешиваются двенадцатью бусинами. Морская раковина уравновешивается одним кубиком и восемью бусинами. Сколькими бусинами уравновесится одна морская раковина?
Решение
Эталон записи решения задачи в тетради:
Дано: Рассуждения:
Кубик (К) ЗК+Р= 12Б, (1) Раковина (Р) (2)
Бусина (Б) Подставим выражение для Р из (2) в (1). Получим:
Найти: 4k + 12Б,
4k = 4Б, Каков вес раковины в бусинах? (3)
Подставим выражение для К из (З) в (2). Получим:
Р = Б + 8Б,
Ответ: вес раковины равен весу девяти бусин.
Задача 47. Вес бутылки
Бутылка уравновешивается на чашечных весах тарелкой и стаканом. Два кувшина уравновешиваются тремя тарелками. Бутылка и стакан уравновешиваются кувшином. Сколько стаканов уравновесят бутылку?
Решение
Эталон записи решения задачи в тетради:
Дано: Рассуждения:
Бутылка (Б) Б=Т+С, (1)
Тарелка (Т) ж = зт, (2)
Стакан (С) (З)
Подставим выражение для К
Кувшин (К) из (З) в (2). Получим:
2Б + зт. (4) Надо:
Подставим выражение для Б
Каков вес бутылки из (1) в (4). Получим: в стаканах?
21' +2C + зт.
Сократим обе части равенства на 2Т . Получим:
(5) Подставим выражение для Т из (5) в (1). Получим:
Б = 40 + с,
Ответ: бутылка уравновешивается пятью стаканами.
зо
Задача 48. Вес персиков
На чашечных весах три яблока и одна груша уравновешиваются десятью персиками, а одно яблоко и шесть персиков уравновешиваются одной грушей. Сколько персиков уравновешивают одну грушу?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Яблоки (Я) Груши (Г) |
|
Надо: Каков вес груши в персиках? |
Рассуждения:
зя + г = 10п, (1)
(2)
Подставим выражение для Г из (2) в (1). Получим:
+ = 10П.
Сократим обе части равенства на 6П. Получим:
Подставим выражение для Я из (З) в (1). Получим:
зпч-г- 10П,
Ответ: груша уравновешивается семью персиками.
Иногда
учащиеся не справляются с задачей из-за того, что не понимают ее содержания.
Поэтому необходимо развивать навыки изображения исходных данных задачи и
рассуждений в виде схем и таблиц, которые, являясь наглядным графическим
представлением информации, ускоряют и облегчают процесс решения задачи.
 |
Чтобы учащиеся понимали, какие элементы рассуждений даны, а какие получены по доказательству, предлагается проводить линии разных цветов (например, красным и синим карандашами).
С помощью таблиц решаются задачи с четырьмя, пятью и более парами элементов, когда использование схем неудобно и недостаточно наглядно из-за их чрезмерной громоздкости.
Возможно решение подобных задач и с помощью законов алгебры логики.
Для учащихся 4—9 классов.
Задача 1. Одноклассницы
Аня и Таня имеют фамилии Строгова и Добрынина. Какую фамилию имеет каждая из девочек, если известно, что Таня и Добрынина — одноклассницы?
Решение
Ученики проговаривают условие задачи и записывают его в тетрадь:
1. Даны имена девочек: Аня и Таня. Обозначим их символьными переменными А и Т соответственно и запишем в графу «Дано: » .
2. Даны фамилии девочек: Строгова и Добрынина. Обозначим их символьными переменными С и Д соответственно и запишем в графу «Дано: » .
З. В задаче требуется узнать, какую фамилию имеет каждая девочка; запишем этот вопрос в графу «Надо: » .
4. В графе «Рассуждения:» запишем в первый столбик символьные переменные, соответствующие именам, а во второй — символьные переменные, соответствующие фамилиям.
|
Дано: Аня (А) Таня (Т) Строгова (С) Добрынина (Д) |
|
Надо: Кто какую фамилию имеет? |
 |
т с
Далее ученики анализируют условие задачи и строят свои рассуждения, отмечая выводы на схеме и одновременно записывая их. При этом важно, чтобы ребята указывали, откуда следует вывод — из условия задачи или из доказанного ранее.
Рассуждения ученика:
1. Таня
не Добрынина (по условию, они 
одноклассницы, а значит, разные девочки).
Покажем на схеме пунктирной линией отсутствие соответствия между символьными
переменными Т и Д (синим цветом). Значит, Таня — Строгова. Покажем соответствие
между символьными переменными Т и С сплошной линией (красным цветом).
2. Так как Таня Строгова (по доказательству), Аня — не Строгова. Покажем на схеме пунктирной линией отсутствие соответствия между символьными переменными А и С (красным цветом).
З. Так как Аня — не Строгова (по доказательству), Аня — Добрынина. Покажем соответствие между символьными переменными А и Д сплошной линией (красным цветом).
4. Итак, рассуждая, мы пришли к выводу: Аня имеет фамилию Добрынина, а Таня — Строгова. Эталон записи решения задачи в тетради:
|
Дано: Аня (А) Таня (Т) Строгова (С) Добрынина (Д) |
|
Надо: Кто какую фамилию имеет? |
Рассуждения:
-с
1. Так как Таня не Добрынина (по условию), значит, Таня — Строгова.
2.
 |
З. Так как Аня — не Строгова (по доказательству), значит, Аня — Добрынина.
Ответ: Таня имеет фамилию Строгова, Аня — Добрынина.
Задача 2. Друзья
Петя и Миша имеют фамилии Белов и Чернов. Какую фамилию имеет каждый из ребят, если Петя на два года старше Белова?
Ответ: Петя имеет фамилию Чернов, Миша
Белов.
Задача З. Подруги
Света и Наташа имеют фамилии Корчагина и Петрова. Какую фамилию имеет каждая девочка, если Света и Корчагина живут в соседних домах?
Ответ: Света имеет фамилию Петрова,
Наташа 
Корчагина.
2-1703
Задачи такого типа можно постепенно усложнять путем увеличения количества элементов, но между этими элементами обязательно должно быть взаимно однозначное соответствие.
Задача 4. У кого какая оценка?
Когда Аня, Женя и Нина спросили, какие им поставили оценки за контрольную работу по математике, учительница ответила: «Попробуйте догадаться сами, если я скажу, что в вашем классе «двоек» нет, а у вас троих оценки разные, причем:
• у Ани — не «тройка», 
у Нины — не «тройка» и
не «пятерка». Какую оценку получила каждая из учениц?
Решение
Ученики проговаривают условие задачи и записывают его в тетрадЬ••
1. Даны ученицы — Аня, Женя, Нина; обозначим их символьными переменными: А, Ж и Н соответственно и запишем эти данные в графу «Дано: ».
2. Даны оценки за контрольную работу, Так как
«двоек» нет, а ребята получили разные оценки, это «З», «4» и «5». Запишем эти данные в графу « Дано: ».
З. В задаче требуется узнать, какую оценку получила каждая из учениц; запишем этот вопрос в графу «Надо: » .
4. В графу «Рассуждения: » запишем в первый столбик символьные переменные, соответствующие именам девочек, а во второй — оценки, полученные за контрольную работу.
Дано:Рассуждения:
|
З, 4, 5 |
|
оценку получил? |
Аня (А) З Женя (Ж) 4 Нина
(Н)н 5 Оценки:
Надо:
Кто какую
Рассуждения ученика:
1. У Нины не «З» и не «5» (по условию). Покажем на схеме пунктирной линией отсутствие соответствия между символьной переменной Н и оценками «З» и «5» (синим цветом). Значит, у Нины оценка «4». Покажем соответствие между символьной переменной Н и «4» сплошной линией (красным цветом).
2. Так как у Нины «4» (по доказательству), у Ани и Жени — не «4». Покажем на схеме пунктирными линиями отсутствие соответствия между А и «4», Ж и «4» (красным цветом).
З. Так как у Ани — не «З» (по условию) и не «4» (по доказательству), у Ани оценка «5». Покажем отсутствие соответствия между А и «З» пунктирной линией (синим цветом) и соответствие между А и «5» сплошной линией (красным цветом).
4.
 |
5. Так как у Жени — не «4» и не «5» (по доказательству), у Жени —- «З». Покажем на схеме соответствие между Ж и «З» сплошной линией (красным цветом).
6. Итак,
рассуждая, мы пришли к выводу: у Ани оценка «5», у Нины — «4», у Жени
Эталон записи решения задачи в тетради:
|
Дано: АНЯ (А) Женя (Ж) Нина (Н) Оценки: З, 4, 5 |
|
Надо: Кто какую оценку получил? |
Рассуждения:
1. Так
как (по условию) у Нины не «З» и не «5», у Нины —
2. Так как у Нины «4» (по доказательству), у Ани и Жени — не «4».
З. Так как у Ани — не «З» (по условию)
и не «4» (по доказательству), то у Ани
4. Так как у Ани «5» (по доказательству), у Жени — не «5».
5.
Так как у Жени — не «4» и не «5» (по доказательству), у Жени
Ответ: Аня получила оценку «5», Нина
Женя
Задача 5. Праздничный утренник
Галя, Марина и Оля пришли на праздничный утренник в платьях разных цветов — желтом, синем и розовом. Галя была не в желтом, Марина — не в желтом и не в розовом. В платье какого цвета была каждая из девочек?
Ответ: Оля была в желтом платье, Марина — в синем, Галя — в розовом.
Задача 6. Кто где живет?
 |
Ответ: Аня живет на третьем этаже, Вера — на первом, Лиза — на втором.
Задача 7. В каких квартирах живут котята?
В квартирах N2N2 1,
2 и З живут три котенка — белый, черный и рыжий. В квартирах N2N2 1 и 2 живут
не черные котята. Белый котенок живет не в квартире № 1. В какой квартире какой
котенок живет? 
Ответ: рыжий котенок живет в квартире № 1, белый — № 2, черный — № З.
Задача 8. Кто какую игрушку спрятал?
Играя, каждая из трех подруг — Катя, Галя
и Оля 
опустили в свои мешочки одну из трех
игрушек — медвежонка, зайчика, слоника. Оля не прятала ни зайчика, ни
медвежонка. Катя спрятала зайчика. Они предлагают узнать, у кого какая игрушка
находится в мешочке.
Ответ: у Оли в мешочке спрятан слоник, у Кати — зайчик, у Гали — медвежонок.
Задача 9. Кто каким карандашом раскрашивал?
Три товарища — Витя, Сережа и Коля — раскрашивали рисунки карандашами трех цветов: красным, синим, зеленым. Витя раскрашивал рисунок не красным и не синим карандашом, Коля — не синим карандашом. Каким карандашом раскрашивал свой рисунок каждый мальчик?
Ответ: Витя раскрашивал зеленым карандашом, Коля — красным, Сережа — синим.
Задача 10. Соревнование по бегу
В соревнованиях по бегу Юра, Гриша и Толя заняли три первых места. Какое место занял каждый из мальчинов, если Гриша занял не второе и не третье место, а Толя — не третье?
Ответ: Гриша занял первое место, Толя — второе, Юра — третье.
Задача 11. Три поросенка
 |
Ответ: Ниф-Ниф построил домик из соломы, Наф-Наф — из камня, Нуф-Нуф — из веток.
При решении подобных
задач предпочтение надо отдавать рассуждениям, основанным на полном анализе.
Если выполнен полный анализ, то решение задачи само собой вытекает из
рассуждений. При таких рассуждениях у учащихся развивается не только логическое
мышление, но и речь.
Задача 12. Шашечный турнир
В шашечном турнире каждый из ребят — Миша, Сережа и Яша защищал честь своего класса. Один из них учится в третьем «А», другой — в третьем «Б», третий в третьем «В» классе. Первую партию играл Миша и ученик третьего «А» класса. Вторую партию играл Сережа с учеником третьего «В» класса, а Миша отдыхал. Кто за какой класс играл?
Решение
Ученики проговаривают условие задачи и записывают его в тетрадь:
1. Даны имена мальчиков — Миша, Сережа и Яша. Обозначим их символьными переменными М, С и Я соответственно и запишем эти данные в раздел «Дано: ».
2. Даны обозначения классов, в которых учатся мальчики, — А, Б, В. Запишем эти данные в раздел «Дано: » .
З. В задаче требуется узнать, кто за какой класс играл; запишем этот вопрос в графу «Надо: » .
4. В графе «Рассуждения: » запишем в первый столбик символьные переменные, соответствующие именам мальчиков, а во второй обозначения классов, в которых они учатся, — ЗА, ЗВ, ЗВ.
|
Дано: Миша (М) Сережа (С) Яша (Я) Классы: ЗБ зв |
|
Надо: Кто за какой класс играл? |
Рассуждения: м ЗА
 |
Рассуждения ученика:
1. Так как (по условию) первую партию играл Миша и ученик ЗА класса, значит, Миша — ученик не ЗА класса. Покажем на схеме пунктирной линией отсутствие соответствия между символьной переменной М и обозначением класса ЗА.
2. Так как вторую партию играл Сережа с учеником ЗВ класса, а Миша отдыхал (по условию задачи), Сереэка и Миша — ученики не ЗВ класса. Покажем на схеме пунктирной линией отсутствие соответствия между М и ЗВ, С и ЗВ.
З. Так как Миша учится не в ЗА и не в ЗВ классе (по доказательству), Миша — ученик ЗБ класса. Покажем на схеме сплошной линией соответствие между символьной переменной М и обозначением класса ЗБ.
4. Так как Миша — ученик ЗБ класса (по доказательству), Сережа и Яша — ученики не ЗБ класса. Покажем отсутствие соответствия между С и ЗВ, Я и ЗБ пунктирной линией.
5. Так как Сережа — ученик не ЗВ класса (по условию) и не ЗБ класса (по доказательству), Сережа учится в ЗА классе. Покажем на схеме сплошной линией соответствие между символьной переменной С и обозначением класса ЗА.
6. Так как Сережа — ученик ЗА класса (по доказательству), Яша в этом классе не учится. Покажем отсутствие соответствия между символьной переменной Я и обозначением класса ЗА пунктирной линией.
7.
 |
8. Итак, рассуждая, мы пришли к выводу: Сережа защищал в шашечном турнире честь ЗА класса, Миша — ЗБ класса, Яша — ЗВ класса.
Эталон записи решения задачи в тетради:
|
Дано: Миша (М) Сережа (С) Яша (Я)
ЗБ зв |
|
Надо: Кто за какой класс играл? |
Рассуждения:
1. Так как (по условию) первую партию играл Миша и ученик ЗА класса, Миша — ученик не ЗА класса.
2. Так как вторую партию играл Сережа с учеником ЗВ класса, а Миша отдыхал (по условию), Сережа и Миша — ученики не ЗВ класса.
З. Так как Миша учится не в ЗА и не в ЗВ классе (по доказательству), Миша — ученик ЗБ класса.
4. Так как Миша — ученик ЗБ класса (по доказательству), Сережа и Яша — ученики не ЗБ класса.
5. Так как Сережа — ученик не ЗВ класса (по условию) и не ЗБ класса (по доказательству), Сережа учится в ЗА классе.
6. Так как Сережа — ученик ЗА класса (по доказательству), Яша в этом классе не учится.
7. Так как Яша ученик не ЗА и не ЗБ класса, Яша — ученик ЗВ класса.
Ответ: Сережа играл в шашечном турнире за ЗА класс, Миша — за ЗБ класс, Яша — за ЗВ класс.
Задача 13. Как зовут сестер?
 |
Ответ: сестра Володи — Галя, Димы — Оля, Аркаши — Лена.
Задача 14. Одноклассницы
Три одноклассницы — Соня, Таня и Женя —
занимаются в разных спортивных секциях: одна из них 
в гимнастической,
другая — в лыжной, третья — в секции плавания. Каким видом спорта занимается
каждая из них, если известно, что Соня плаванием никогда не увлекалась, Таня в
лыжную секцию никогда не ходила, а Женя является победительницей в
соревнованиях по лыжам?
Ответ: Таня занимается плаванием, Женя — лыжами, Соня — гимнастикой.
Задача 15. У кого какая фамилия?
В одном классе
учатся Иван, Петр, Сергей. Их фамилии Петров, Иванов и Сергеев. Установите
фамилию каждого из ребят, если известно, что фамилия Ивана 
не Иванов,
Петра — не Петров, Сергея — не Сергеев и что Сергей живет в одном доме с
Петровым.
Ответ: фамилии Сергея — Иванов, Петра — Сергеев, Ивана — Петров.
Задача 16. У кого какой цвет волос?
Встретились трое друзей — Белов, Чернов и Рыжов. Один из них блондин, другой — брюнет, третий — рыжий. Брюнет сказал Белову: «Ни у одного из нас цвет волос не соответствует фамилии». Какой цвет волос у каждого из них, если известно, что брюнет всегда говорит правду?
Ответ: Белов рыжий, Чернов блондин, Рыэков — брюнет.
 |
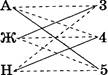
Сидели как-то на берегу реки три школьных товарища и вели неторопливую беседу. Фамилия одного из этих ребят — Токарев, второго — Слесарев, а третьего — Плотников. Отец одного из школьников работает плотником, второго — токарем, третьего — слесарем.
— Интересно, — сказал мальчик, отец которого был слесарем, — что ни один из наших отцов не работает по той специальности, от которой произошла его фамилия.
А ты ведь
прав, подтвердил после раздумий Плотников.
Кем работают отцы ребят?
Ответ: Слесарев работает плотником,
Токарев 
слесарем, Плотников — токарем.
Задача 18. Друзья
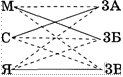
На одном заводе работают три друга слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер. Он — самый младший из друзей. Семенов, женатый на сестре Борисова, старше токаря. Назовите фамилии слесаря, токаря и сварщика.
Ответ: Иванов — слесарь, Семенов — сварщик, Борисов — токарь.
Задача 19. Трое с одной улицы
Кондратьев, Давыдов и Федоров живут на
одной улице. Один из них — столяр, другой — маляр, третий 
водопроводчик.
Недавно Давыдов хотел попросить столяра, который был его старым знакомым,
сделать кое-что для своей квартиры, но ему сказали, что столяр работает в доме
водопроводчика. Известно также, что Федоров никогда не слышал о Давыдове. У
кого какая профессия?
Ответ: Давыдов — маляр, Федоров — водопроводчик, Кондратьев — столяр.
Задача 20. Коробки и крупы
 |
Ответ: в банке с надписью «Гречка» находится манка.
Задача 21. Крепежные принадлежности
У мальчика Димы в трех коробках лежали гвозди, винты и гайки. На каждой коробке было написано, что в ней лежит. Однажды младший брат Димы Алеша пересыпал содержимое коробок так, что надпись на каждой коробке перестала соответствовать ее содержимому. Хорошо еще, что гвозди остались лежать отдельно от гаек и винтов и т. д. Когда Дима открыл коробку с надписью «Гвозди», обнаружил в ней винты. Что было написано на коробке, в которой лежали гвозди, и на коробке, в которой лежали гайки?
Ответ: на коробке, в которой лежали гвозди, было написано «Гайки»; на коробке, в которой лежали гайки, было написано «Винты» .
Золушка
Мачеха, уезжая на бал, дала Золушке мешок, в котором были перемешаны рис и пшено, и велела перебрать их. Когда Золушка уезжала на бал, она оставила три мешка: в одном было пшено, в другом — рис, а в третьем — еще не разобранная смесь. Чтобы не перепутать мешки, Золушка к каждому из них прикрепила по табличке: «Рис», «Пшено» и «Смесь». Мачеха вернулась с бала первой и нарочно поменяла местами все таблички так, чтобы на каждом мешке оказалась неправильная надпись. Ученик феи успел предупредить Золушку, что теперь ни одна надпись на мешках не соответствует действительности. Золушка зачерпнула горсть зернышек из мешка с надписью «Рис» там оказалось только одно пшено. В каком мешке находится рис?
Ответ: рис находится в мешке с надписью «Смесь» . Задача 23. Кто с кем проводит свободное время?
 |
Ответ: Марат проводит время со Светой.
Задача 24. Друзья из летнего лагеря
В летний лагерь
приехали три друга — Миша, Володя и Петя. Известно, что их фамилии — Иванов,
Семенов и Герасимов. Миша — не Герасимов. Володя учится в шестом классе,
Герасимов — в пятом. Отец Володи 
инженер, отец Иванова слесарь. Какая
фамилия у каждого из ребят?
Ответ: фамилия Миши — Иванов, Володи — Семенов, Пети — Герасимов.
Задача 25. Кто на чем ездит домой?
Три друга — Алеша, Боря и Витя — учатся в одном классе. Один из них ездит в школу на трамвае, другой — на троллейбусе, а третий — на автобусе. Однажды после уроков Алеша пошел проводить своего друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!» Кто на чем ездит домой?
Ответ: Алеша ездит на трамвае, Боря — на автобусе, Витя — на троллейбусе.
Теперь рассмотрим более сложные задачи, в которых количество пар элементов увеличено до четырех.
Задача 26. Братья
Четыре брата — Юра, Петя, Володя и Коля — учатся в первом, во втором, в третьем и в пятом классах. Историю начинают изучать с пятого класса. Петя учится только на «4» и «5», а младшие братья стараются брать с него пример. Володя уже изучает историю. Юра помогает решать задачи младшему брату. Кто из них в каком классе учится?
 |
Задача 27. Гимнастика
В соревнованиях по гимнастике Аня, Вера, Галя и Наташа заняли первые четыре места. Определите, кто какое место занял, если известно, что Галя вторая, Наташа хотя не стала победителем, но в призеры попала, Вера проиграла Ане.
Ответ: Аня заняла первое место, Галя второе, Наташа — третье, Вера — четвертое.
Задача 28. Соревнования
Эдик, Вася, Андрей и Миша заняли первые четыре места в соревнованиях. На вопрос, какие они заняли места, мальчики ответили честно:
— Эдик не занял ни первое и ни третье место; — Вася занял второе место;
— Андрей не проиграл Мише.
Какие места заняли мальчики?
Ответ: Андрей занял первое место, Вася — второе,
Миша — третье, Эдик — четвертое.
Кто сколько забил голов?
Володя, Костя, Дима, Саша играли в хоккей. Один из них не забил ни одного гола, другой — один гол, третий —- два гола, четвертый четыре гола. Известно, что Костя забил меньше четырех голов. Володя, как ни старался, все время не попадал в ворота, а Дима забил один гол. Кто сколько забил голов?
Ответ: Володя не забил ни одного гола, Дима забил один гол, Костя —- два гола, Саша — четыре гола.
Задача 30. Веселые принцессы
Жили-были во дворце четыре веселые принцессы 
Наталия, Ольга, Диана и Маргарита. Они очень любили посмеяться. Придворные знали, сколько смеялась каждая принцесса каждый день. Принцессы смеялись 2, 5, 7, 10 минут. Наталия не могла смеяться дольше 2 минут, Маргарита смеялась 10 минут, Ольга смеялась меньше Дианы. Сколько минут смеялась каждая принцесса?
 |
Задача 31. Артек
Боря, Витя, Гриша и Егор встретились и подружились в летнем лагере «Артек». Они приехали сюда из разных городов: один из Твери, другой — из Омска, третий — из Екатеринбурга, четвертый — из Казани. Из какого города приехал каждый, если известно, что:
1) Боря и мальчик из Казани жили в одной комнате;
2) Боря никогда не был ни в Твери, ни в Екатеринбурге;
З) Гриша играл в волейбол в одной команде с мальчиком из Твери, а против них обычно сражался их приятель из Казани;
4) Егор и мальчик из Твери увлекались игрой в шахматы.
Ответ: Гриша приехал из Екатеринбурга,
Витя 
из Твери, Боря из Омска, Егор — из Казани.
Задача Возраст детей
В семье четверо детей, им 5, 8, 13, 15 лет. Детей зовуг Аня, Боря, Вера и Галя. Сколько лет каждому ребенку, если одна девочка ходит в детский сад, Аня старше Бори и сумма лет Ани и Веры делится на З?
Ответ: Вере — 5 лет, Боре — 8 лет, Ане — 13 лет, Гале — 15 лет.
Задача 33. Первые буквы фамилий
Ваня, Петя, Саша и Коля носят фамилии, начинающиеся с букв «В», «П», «С» и «К». Известно, что:
1) Ваня и С. — отличники;
2) Петя и В. — троечники;
З) В. и Коля ростом ниже П.;
4) Саша и Петя имеют одинаковый рост.
 |
Задача 34. В каком сосуде какая жидкость?
В бутылке, стакане, кувшине и банке находится молоко, лимонад, квас и вода. Известно, что вода и молоко — не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке — не лимонад и не вода. Стакан стоит около сосуда с молоком. В какой сосуд налита каждая из жидкостей?
Ответ: молоко налито в кувшин, лимонад в бутылку, квас — в банку, вода — в стакан.
Задача 35. Имена и фамилии
Имена Иванова, Петрова, Семенова и
Николаева 
Иван, Петр, Семен и Николай, причем только
у Николаева фамилия происходит от его же имени. Семенова зовут не Петром.
Назовите фамилию и имя каждого.
Ответ: фамилия Петра — Иванов, Семена — Петров, Ивана Семенов, Николая — Николаев.
Тетради учеников
На столе лежат три пачки тетрадей.
На 1-й пачке написано «10 класс».
На 2-й пачке написано «5 класс или 7 класс».
На 3-й пачке написано «7 класс».
Известно, что ни одна надпись не верна. В какой пачке какие тетради?
Решение
Рассуждения ученика:
Так как (по условию) ни одна надпись не верна, в первой пачке тетради не 10 класса, во второй — не 5 и не 7 класса, в третьей — не 7 класса. Покажем отсутствие соответствия на схеме пунктирными линиями.
1-я пачка- -- тетради 5 класса
2-я пачка-тетради 7 класса
3-я пачка- тетради 10 класса
 |
1-я пачка- -
тетради 5 класса
2-я пачка7 класса
3-я пачка--= тетради 10 класса
Так как в третьей пачке тетради не 7 класса (по условию) и не 10 класса (по доказательству), в ней тетради 5 класса. Продемонстрируем рассуждения на схеме сплошной линией.
Получаем, что в пЬрвой пачке тетради 7 класса. Покажем соответствие на схеме сплошной линией.
1-я пачкатетради 5 класса
2-я пачктетради 7 класса
3-я пачка тетради 10 класса
Ответ: в первой пачке тетради 7 класса, во второй — 10 класса, в третьей — 5 класса.
Задача Выставка
На трех указателях экспозиций выставки имеются следующие надписи:
• на первом — «Экспозиция Русского музея»;
• на втором «Экспозиция Эрмитажа или Русского
музея » ;
• на третьем «Экспозиция Музея-квартиры А. С. Пушкина».
Известно, что все надписи на указателях экспозиции не соответствуют друг другу.
Определите истинные надписи для экспозиций музеев.
Ответ: на первом указателе должна быть надпись «Экспозиция Эрмитажа», на втором — «Экспозиция Музея-квартиры А. С. Пушкина» , на третьем — «Экспозиция Русского музея» .
Задача 38. Поезда
 |
Ответ: на первом перроне стоял поезд на Псков, на втором — на Вологду, на третьем — на Новгород.
Задача 39. ЗАМОК
В одном королевстве жили незамужние
принцессы и голодные тигры. Всякому узнику, осужденному на смерть, король этого
королевства давал последний шанс спастись. Ему предлагалось войти в одну из
трех комнат. В одной из них находилась принцесса, в другой — тигр, а третья
комната была пустой. Если в комнате не оказывалось тигра, узник был спасен.
Выбор надо было сделать на основании табличек на дверях комнат. На первой
табличке было написано «Здесь находится принцесса или тигр», на второй табличке
«Здесь
находится тигр», на третьей табличке «Эта комната пуста» .
Узнику было известно, что таблички на дверях не соответствуют тому, что в них находится. Какие двери мог выбрать узник, чтобы остаться живым?
Решение
Покажем, как задачи этого типа можно решать с помощью алгебры логики, и проверим на схеме. Введем обозначения:
П — в комнате находится принцесса;
П — в комнате не находится принцесса;
Т — в комнате находится тигр;
Т — в комнате не находится тигр.
Утверждение на первой двери: П v Т.
Утверждение на второй двери: Т.
Утверждение на третьей двери: П Т.
Рассуждения ученика:
1. Так как надписи на табличках не соответствуют действительности, для первой комнаты будет истинным
 |
Значит, первая комната — пустая. Проведем соответствующие линии.
1-я табл.здесь
находится тигр
2-я табл.здесь находится принцесса 3-я табл.эта комната пустая
2. Во второй комнате находится не тигр, так как на ней надпись «Здесь находится тигр», и она не пустая (по доказательству), тогда во второй комнате находится принцесса. Проведем соответствующие линии.
1-я табл.- здесь находится тигр
2-я табл.здесь находится принцесса
3-я табл.эта комната пустая
З. Так как первая комната пуста (по доказательству), а во второй находится принцесса (тоже по доказательству), в третьей комнате находится тигр. Проведем соответствующие линии.
Ответ: узник должен выбрать или первую комнату, которая пуста, или вторую, где находится принцесса.
Задача 40. Змея
На первом месте по величине из змей находится анаконда или индийский питон, на втором месте — королевский питон, а на третьем месте — анаконда. Какая змея занимает какое место по величине, если известно, что ни одно из высказываний не является истинным?
Ответ: на первом месте королевский питон, на втором месте — анаконда, на третьем — индийский питон.
Задача 41. Мороженое
Детям купили мороженое. На обертках надписи: «сливочное», «малиновое или шоколадное», «шоколад-
Ни одна надпись не соответствует сорту мороженого. Какое мороженое в какой обертке находится?
Решение
Рассуждения ученика:
Решим задачу с помощью алгебры логики.
Введем обозначения:
С — в обертке сливочное мороженое;
М — в обертке малиновое мороженое;
Ш — в обертке шоколадное мороженое.
1. Так как ни одна из оберток не соответствует сорту мороженого, для второй обертки будет истинно высказывание:
Ш v М = Ш & М (по закону Моргана).
Тогда во второй обертке — сливочное мороженое.
2. В третьей обертке — не шоколадное мороженое, так как на ней надпись «шоколадное мороженое», и не сливочное мороженое (по доказательству). Значит, там малиновое мороженое.
З. Во второй обертке сливочное мороженое, в третьей малиновое (по доказательству), тогда в первой обертке —- шоколадное.
1-я обертка«
сливочное»
2-я обертк«малиновое»
3-я обертка« шоколадное»
Ответ: в первой обертке — шоколадное мороженое, во второй — сливочное, в третьей малиновое.
Задача 42. Обезьяны
На трех клетках в зоопарке висят таблички. На первой табличке написано, что в клетке сидит горилла, на второй — что в клетке сидит орангутанг или шимпанзе, а на третьей — что в клетке сидит шимпанзе. Известно, что надписи на всех табличках не соответствуют содержимому клеток. Какая обезьяна в какой клетке сидит?
Ответ: в первой клетке — шимпанзе, во второй
горилла,
в третьей — орангутанг.
Задача 43. Соревнование по бегу
В соревнованиях по
бегу первое место занял медведь или лиса, второе место занял заяц, а третье
место 
медведь. Все эти утверждения не
соответствуют действительности. Какое место заняли медведь, лиса, заяц?
Ответ: на первом месте — заяц, на втором — медведь, на третьем — лиса.
Дальнейшее увеличение
количества элементов в условии задачи ведет к нагроможденности линий в схемах.
Поэтому более сложные задачи легче ретать с помощью таблиц.
Задача 44. Школьные учителя
В старших классах работают три учителя: Воронов, Соколов и Коршунов. Каждый из них преподает по два предмета, так что в расписании у них всего шесть предметов: математика, физика, химия, история, литература и английский язык. Коршунов — самый молодой из преподавателей. Учитель химии старше учителя истории. Все трое — учитель химии, учитель физики и Соколов занимаются спортом. Когда между учителями литературы и английского языка возникает спор, Коршунов тоже принимает участие в споре. Соколов не преподает ни английский язык, ни математику. Кто какие предметы преподает?
Решение
|
Дано: Воронов Соколов Коршунов математика физика химия история литература английский язык |
|
Надо: Кто какие предметы преподает? |
|
|
|
Предмет |
||||
|
|
|
|
|
ф |
|
|
|
Воронов |
|
|
|
|
|
|
|
Соколов |
|
|
|
|
|
|
|
Коршунов |
|
|
|
|
|
|
 |
Рассуждения ученика:
1. Так как учитель химии, учитель физики и Соколов занимаются спортом (по условию), Соколов не учитель физики и не учитель химии. Ставим минусы в ячейки «Соколов, Химия» и «Соколов, Физика».
2. Так как Коршунов принимает участие в споре между учителем литературы и учителем английского языка (по условию), Коршунов не учитель литературы и не учитель английского языка. Ставим минусы в ячейки: «Коршунов, Литература» и «Коршунов, Английский язык».
З. Соколов не преподает ни английский язык, ни математику (по условию). Ставим минусы в ячейки «Соколов, Английский язык» и «Соколов, Математика» .
4. Так как Коршунов — самый молодой из преподавателей, а учитель химии старше учителя истории (по условию), Коршунов не является учителем химии. Ставим минус в ячейку «Коршунов, Химия».
 |
|
|
Предмет |
|||||
|
|
|
|
|
|
|
|
|
Воронов |
|
|
|
|
|
|
|
Соколов |
|
|
|
|
|
|
|
Коршунов |
|
|
|
|
|
|
5. Каждый учитель преподает по два предмета (по условию). Из таблицы видно, что Соколов преподает историю и литературу (методом исключения). Ставим плюсы в ячейки «Соколов, История» и «Соколов, Литература» и заполняем минусами остальные ячейки столбцов «История» и «Литература».
|
|
Предмет |
|||||
|
|
|
|
|
|
|
|
|
Воронов |
|
|
|
|
|
|
|
Соколов |
|
|
|
|
|
|
|
Коршунов |
|
|
|
|
|
|
6. Тогда Коршунов ведет математику и физику (методом исключения). Заполняем плюсами и минусами соответствующие ячейки столбцов «Математика» и «Физика».
|
|
Предмет |
|||||
|
|
|
|
|
|
|
|
|
Воронов |
|
|
|
|
|
|
|
Соколов |
|
|
|
|
|
|
|
Коршунов |
|
|
|
|
|
|
7.
 |
|
|
Предмет |
|||||
|
|
|
|
|
|
|
|
|
Воронов |
|
|
|
|
|
|
|
Соколов |
|
|
|
|
|
|
|
Коршунов |
|
|
|
|
|
|
Ответ: Коршунов преподает физику и математику, Соколов историю и литературу, Воронов — химию и английский язык.
В некоторых задачах данного раздела вместо плюсов и минусов в ячейках таблицы мы будем ставить единицы и нули.
Задача 45. Спортивные соревнования
Коля, Боря, Вова и Юра заняли первые четыре места в спортивном соревновании. На вопрос, какие места они заняли, они честно ответили:
— Коля не занял ни первое, ни четвертое место; — Боря занял второе место; — Вова не был последним.
Какое место занял каждый мальчик?
Решение
1.
 |
|
Мальчик |
|
Призовое место |
|
|
|
1 |
2 |
з |
4 |
|
|
Коля |
|
|
|
|
|
Боря |
|
1 |
|
|
|
Вова |
|
|
|
|
|
юра |
|
|
|
|
2. Так как Коля не занял ни первое, ни четвертое место (по условию) и не занял второе место, которое занял Боря (по условию), он занял третье место. Ставим в ячейку «Коля, З» цифру 1. Значит, Вова и Юра не могут занимать третье место. Ставим в ячейки «Вова, З», «Юра, З» цифру О.
З. Так как Вова не занял четвертое место (по условию), не занял второе место, так как его занял Боря (по условию), и не занял третье место (по доказательству), он занял первое место, а Юра — четвертое. Ставим в ячейку «Вова, 1» цифру 1, в ячейку «Юра, 1» — цифру О, а в ячейку «Юра, 4» — цифру 1.)
|
Мальчик |
|
Призовое место |
|
|
|
1 |
2 |
з |
4 |
|
|
Коля |
о |
|
1 |
|
|
Боря |
|
1 |
|
|
|
Вова |
1 |
|
|
|
|
юра |
|
О |
|
1 |
 |
Задача 46. У кого какая профессия?
Корнеев, Докшин, Мареев и Скобелев жители нашего города. Их профессии — пекарь, врач, инженер и милиционер.
Известно, что:
1) Корнеев и Докшин — соседи и всегда ездят на работу вместе;
2) Докшин старше Мареева;
З) Корнеев регулярно обыгрывает Скобелева в настольный теннис;
4) пекарь на работу всегда ходит пешком;
5) милиционер живет не рядом с врачом;
6) инженер и милиционер встречались один раз, когда милиционер оштрафовал инженера за нарушение правил уличного движения;
7) милиционер старше врача и инженера.
Определите, кто чем занимается.
Решение
1. Так как Корнеев и Докшин ездят на работу, а пекарь ходит пешком (по условиям 1 и 4), они не пекари. Ставим минусы в ячейки «Пекарь, Корнеев» , «Пекарь, Докшин».
|
Профессия |
|
Фамилия |
|
|
|
Корнеев |
Докшин |
Мареев |
Скобелев |
|
|
Пекарь |
|
|
|
|
|
Врач |
|
|
|
|
|
Инженер |
|
|
|
|
|
Милиционер |
|
|
|
|
2.
 |
|
Профессия |
|
Фамилия |
|
|
|
Корнеев |
Докшин |
Мареев |
Скобелев |
|
|
Пекарь |
|
|
|
|
|
Врач |
|
|
|
|
|
Инженер |
|
|
|
|
|
Милиционер |
|
|
|
|
З. Милиционер старше врача и инженера (по доказательству — Корнеева и Докшина), а Докшин старше Мареева (по условию 2), значит, Мареев не милиционер. Следовательно, милиционер Скобелев . Ставим плюс в ячейку «Милиционер, Скобелев» , а в остальные ячейки строки «Милиционер» и столбца «Скобелев» ставим минусы.
|
Профессия |
|
Фамилия |
|
|
|
Корнеев |
Докшин |
Мареев |
Скобелев |
|
|
Пекарь |
|
|
|
|
|
Врач |
|
|
|
|
|
Инженер |
|
|
|
|
|
Милиционер |
|
|
|
|
4. Из таблицы видно, что Мареев пекарь. Ставим плюс в ячейку «Пекарь, Мареев» и минусы в остальные ячейки столбца «Мареев».
|
Профессия |
|
Фамилия |
|
|
|
Корнеев |
Докшин |
Мареев |
Скобелев |
|
|
Пекарь |
|
|
|
|
|
Врач |
|
|
|
|
|
Инженер |
|
|
|
|
|
Милиционер |
|
|
|
|
5.
 |
врач, а Докшин — инженер. Ставим плюсы в
ячейки «Врач, Корнеев», «Инженер, Докшин» и минусы в остальные ячейки.
|
Профессия |
|
Фамилия |
|
|
|
Корнеев |
Докшин |
Мареев |
Скобелев |
|
|
Пекарь |
|
|
|
|
|
Врач |
|
|
|
|
|
Инженер |
|
|
|
|
|
Милиционер |
|
|
|
|
Ответ: Корнеев врач, Докшин инженер, Мареев — пекарь, Скобелев — милиционер.
Задача 47. Отели
Четыре друга Владимир, Андрей, Александр и Михаил — решили отдохнуть на Канарских островах. Поехав на остров Тенерифе, они все поселились в разных отелях: «Тропикаль», «Конкордия», «Флорида» и «Ла Паз».
Известно, что:
1) Владимир проводил своих друзей в отель «Ла Паз» и отель «Тропикаль»;
2) человек, поселившийся в отеле «Ла Паз», — лучший друг Андрея;
З) житель отеля «Флорида» встречается с Владимиром и Михаилом у моря;
4) Андрей приходит обедать в отель «Флорида» к своему товарищу.
Кто в каком отеле живет?
Решение
1.
 |
|
Имя |
Отель |
|||
|
«Тропикаль» |
«Конкордия» |
«Ла Паз» |
«Флорида» |
|
|
Владимир |
|
|
|
|
|
Михаил |
|
|
|
|
|
Александр |
|
|
|
|
|
Андрей |
|
|
|
|
2. Из таблицы видно, что Владимир живет в отеле «Конкордия». Ставим плюс в ячейку «Владимир, Конкордия» и минусы во все остальные ячейки столбца «Конкордия» .
|
Имя |
Отель |
|
||
|
«Тропикаль» |
«Конкордия» |
«Ла Паз» |
« Флорида» |
|
|
Владимир |
|
|
|
|
|
Михаил |
|
|
|
|
|
Александр |
|
|
|
|
|
Андрей |
|
|
|
|
З. Из условия 4 следует, что Андрей не живет в отеле «Флорида». Ставим минус в ячейку «Андрей, Флорида».
|
Имя |
Отель |
|
||
|
«Тропикаль» |
«Конкордия» |
«Ла Паз» |
«Флорида» |
|
|
Владимир |
|
|
|
|
|
Михаил |
|
|
|
|
|
Александр |
|
|
|
|
|
Андрей |
|
|
|
|
 |
4.
Анализируя таблицу, делаем вывод, что Андрей живет в отеле «Тропикаль», а
Александр в отеле «Флорида». Ставим плюс в ячейку «Андрей, Тропикаль», минусы в
остальные ячейки столбца «Тропикаль», плюс в ячейку «Александр, Флорида» и
минус в оставшуюся ячейку строки «Александр».
|
Имя |
Отель |
|||
|
«Тропикаль» |
«Конкордия» |
«Ла Паз» |
«Флорида» |
|
|
Владимир |
|
|
|
|
|
Михаил |
|
|
|
|
|
Александр |
|
|
|
|
|
Андрей |
|
|
|
|
5. Из таблицы видно, что Михаил живет в отеле «Ла Паз». Ставим плюс в ячейку «Михаил, Ла Паз».
|
Имя |
Отель |
|
||
|
«Тропикаль» |
«Конкордия» |
«Ла Паз» |
« Флорида» |
|
|
Владимир |
|
|
|
|
|
Михаил |
|
|
|
|
|
Александр |
|
|
|
|
|
Андрей |
|
|
|
|
Ответ: Владимир живет в отеле « Конкордия » , Михаил — в отеле «Ла Паз», Александр в отеле «Флорида», Андрей — в отеле «Тропикаль ».
Задача 48. Четыре инженера
Борисов, Кириллов, Данин и Савин инженеры. Один из них автомеханик, другой химик, третий — строитель, четвертый — радиотехник.
Известно, что:
1)
 |
Кириллова, но
проигрывает Савину, ходит на лыжах лучше Кириллова, который моложе его, и лучше
радиотехника, а также посещает театр вдвое чаще, чем тот инженер, который
моложе его и Кириллова;
2) химик, который посещает театр вдвое чаще, чем автомеханик, не является самым молодым, а старше его только один из инженеров;
З) строитель, который на лыжах ходит хуже, чем радиотехник, как правило, проигрывает в шахматных сражениях автомеханику;
4) самый старший из инженеров лучше всех играет в шахматы и чаще всех бывает в театре, а самый молодой лучше всех ходит на лыжах;
5) радиотехник лучший шахматист и самый заядлый театрал, а автомеханик — лучший лыжник.
Назовите профессию каждого из инженеров.
Упорядочите инженеров по возрасту начиная с наибольшего, а лыжников и шахматистов по степени мастерства начиная с наибольшей.
Решение
1. Так как Борисов обыгрывает в шахматы Данина и Кириллова, проигрывает Савину, а самый старший играет в шахматы лучше всех (по условиям 1, 4), Савин — самый старший, и он радиотехник (это следует из условия 5). Ставим плюс в ячейку «Савин, Радиотехник», а все остальные ячейки строки «Савин» и столбца «Радиотехник» заполняем минусами.
|
Фамилия |
Профессия |
|||
|
Автомеханик |
Химик |
Строитель |
Радиотехник |
|
|
Борисов |
|
|
|
|
|
Кириллов |
|
|
|
|
|
Данин |
|
|
|
|
|
Савин |
|
|
|
|
2.
 |
|
Фамилия |
Профессия |
|||
|
Автомеханик |
Химик |
Строитель |
Радиотехник |
|
|
Борисов |
|
|
|
|
|
Кириллов |
|
|
|
|
|
Данин |
|
|
|
|
|
Савин |
|
|
|
|
З. Строитель ходит на лыжах хуже, чем радиотехник Савин (по условию З) (самый старший по возрасту), а самый молодой ходит на лыжах лучше всех (по условию 4), значит, по старшинству инженеры располагаются так: самый старший — Савин (радиотехник), затем Борисов (химик), строитель и автомеханик (самый молодой).
4. Так
как младше Борисова (химика, по доказательству) два инженера, из которых
Кириллов старший (это следует из условия 1), Савин — самый старший (по
доказательству), а моложе Борисова двое 
строитель и затем
автомеханик (по доказательству), Кириллов строитель а Данин автомеханик .
Ставим плюсы в ячейки «Кириллов, Строитель » , «Данин, Автомеханик» и минусы в
оставшиеся ячейки.
|
Фамилия |
|
Профессия |
|
|
|
Автомеханик |
Химик |
Строитель |
Радиотехник |
|
|
Борисов |
|
|
|
|
|
Кириллов |
|
|
|
|
|
Данин |
|
|
|
|
|
Савин |
|
|
|
|
5.
 |
6. Борисов ходит на лыжах лучше радиотехника Савина (по условию 1 и по доказательству), Савин — лучше, чем строитель Кириллов (по условию З и по доказательству), а Данин (самый молодой) — лучше всех (по условию 4 и по доказательству), значит, порядок лыжников начиная с самого лучшего следующий: Данин, Борисов, Савин, Кириллов.
7. Из
условий 1, 2, З и доказательства следует: Кириллов проигрывает автомеханику
(Данину) и оба они проигрывают Борисову, а лучший шахматист 
Савин (самый
старший). Значит, порядок шахматистов начиная с самого лучшего следующий:
Савин, Борисов, Данин, Кириллов.
Ответ: порядок по возрасту: Савин (самый старший), Борисов, Кириллов, Данин; порядок по лыжному мастерству: Данин (лучший), Борисов, Савин, Кириллов; по шахматному мастерству: Савин (лучший), Борисов, Данин, Кириллов.
Задача 49. На конгрессе
На международном конгрессе встретились четверо ученых: физик, историк, биолог и математик. Национальности их различны, и хотя каждый из ученых владеет двумя языками из четырех (русский, английский, французский и итальянский), нет такого языка, на котором они могут разговаривать вчетвером. Есть язык, на котором могут разговаривать сразу трое, — итальянский. Никто из ученых не владеет французским и русским языками одновременно. Хотя физик не говорит по-английски, но может быть переводчиком, если биолог и ИСТОРИК захотят поговорить друг с другом. Историк может говорить с математиком по-французски. Физик, биолог и математик не могут беседовать втроем на одном языке. Какими двумя языками владеет каждый из ученых?
Решение
 |
|
Ученый |
Язык |
|||
|
Русский |
Английский |
Французский |
Итальянский |
|
|
Физик |
|
|
|
|
|
Историк |
|
|
|
|
|
Биолог |
|
|
|
|
|
Математик |
|
|
|
|
Начнем теперь высказывать предположения и проверять их правильность.
Вариант 1.
Предположим, что историк говорит по-итальянски. Ставим плюс в ячейку «Историк, Итальянский».
1. Два языка, на которых говорит историк, определены. Значит, историк не говорит по-английски. Ставим минус в ячейку «Историк, Английский».
|
Ученый |
Язык |
|||
|
Русский |
Английский |
Французский |
Итальянский |
|
|
Физик |
|
|
|
|
|
Историк |
|
|
|
|
|
Биолог |
|
|
|
|
|
Математик |
|
|
|
|
2.
 |
|
Ученый |
Язык |
|||
|
Русский |
Английский |
Французский |
Итальянский |
|
|
Физик |
|
|
|
|
|
Историк |
|
|
|
|
|
Биолог |
|
|
|
|
|
Математик |
|
|
|
|
З. Физик может быть переводчиком между историком и биологом (по условию), значит, он знает один из языков, которые знает биолог, и один из языков, которые знает историк. Биолог говорит по-русски и по-английски (по доказательству), а физик не говорит по-английски (по условию). Значит, физик гово-
3-1703
рит по-русски. Историк говорит по-француски и по-итальянски (по условию и по предположению), а говорящий по-французски не владеет русским (по условию), значит, физик не говорит по-французски. Следовательно, физик говорит по-итальянски. Ставим плюсы в ячейки «Физик, Русский», «Физик, Итальянский» и минус в оставшуюся ячейку строки « Физик ».
|
Ученый |
Язык |
|||
|
Русский |
Английский |
Французский |
Итальянский |
|
|
Физик |
|
|
|
|
|
Историк |
|
|
|
|
|
Биолог |
|
|
|
|
|
Математик |
|
|
|
|
 |
|
Ученый |
Язык |
|||
|
Русский |
Английский |
Французский |
Итальянский |
|
|
Физик |
|
|
|
|
|
Историк |
|
|
|
|
|
Биолог |
|
|
|
|
|
Математик |
|
|
|
|
Из таблицы видно, что последнее условие задачи выполняется: физик, биолог и математик не могут говорить на одном языке. Значит, наше предположение верно и вариант 1 возможен. Проверим, нет ли других вариантов.
Вариант 2.
Предположим, что историк не говорит по-итальянски. Значит, на итальянском говорят остальные трое: физик, биолог, математик, а это противоречит условию. Значит, это наше предположение неверно. Отсюда следует, что решение задачи однозначно.
Ответ: историк и математик говорят по-французски и по-итальянски; биолог по-русски и по-английски; физик — по-русски и по-италь-
ЯНСКИ.
Задача 50. Студенты
Дина, Соня, Коля, Рома и Миша учатся в институте. Их фамилии: Бойченко, Карпенко, Лысенко, Савченко и Шевченко.
Известно, что:
1) у Ромы нет матери;
2) родители Дины никогда не видели родителей Коли;
З) Шевченко и Бойченко играют в одной баскетбольной команде ;
4)
 |
5) родители Лысенко хорошие друзья родителей Бойченко. Все четверо очень довольны, что их дети собираются пожениться.
Установите имя и фамилию каждого из студентов. Решение
1. Так как у Ромы нет матери (по условию 1), а у Карпенко, Лысенко, Бойченко есть родители и у Шевченко есть мать (по условиям 4 и 5), Рома — Савченко. Ставим плюс в ячейку «Савченко, Рома». Все остальные ячейки столбца «Рома» и строки «Савченко» заполняем минусами.
1 Для сведения: баскетбольная команда может состоять только из юношей или только из девушек.
|
Фамилия |
|
|
Имя |
|
|
|
Дина |
Соня |
Коля |
Рома |
Миша |
|
|
Бойченко |
|
|
|
|
|
|
Карпенко |
|
|
|
|
|
|
Лысенко |
|
|
|
|
|
|
Савченко |
|
|
|
|
|
|
Шевченко |
|
|
|
|
|
 |
Миша. Ставим плюс в ячейку «Карпенко,
Миша» . Все остальные ячейки столбца «Миша» заполняем минусами.
|
Фамилия |
|
|
Имя |
|
|
|
Дина |
Соня |
Коля |
Рома |
Миша |
|
|
Бойченко |
|
|
|
|
|
|
Карпенко |
|
|
|
|
|
|
Лысенко |
|
|
|
|
|
|
Савченко |
|
|
|
|
|
|
Шевченко |
|
|
|
|
|
З. В одной баскетбольной команде играют или девушки, или юноши (по условию З), а Савченко — юноша (по доказательству) и Карпенко — юноша (по условию 4). Значит, Шевченко — не Коля и Бойченко — не Коля; тогда Шевченко и Бойченко — девушки. Отметим сделанные выводы в таблице минусами.
|
Фамилия |
|
|
Имя |
|
|
|
Дина |
Соня |
Коля |
Рома |
Миша |
|
|
Бойченко |
|
|
|
|
|
|
Карпенко |
|
|
|
|
|
|
Лысенко |
|
|
|
|
|
|
Савченко |
|
|
|
|
|
|
Шевченко |
|
|
|
|
|
4. Из таблицы видно, что Коля носит фамилию Лысенко. Ставим плюс в ячейку «Лысенко, Коля» и минусы в остальные ячейки строки «Лысенко».
|
Фамилия |
|
Имя |
|
|
|
|
Дина |
Соня |
Коля |
Рома |
Миша |
|
|
Бойченко |
|
|
|
|
|
|
Карпенко |
|
|
|
|
|
|
Лысенко |
|
|
|
|
|
|
Савченко |
|
|
|
|
|
|
Шевченко |
|
|
|
|
|
5.
 |
|
Фамилия |
имя |
||||
|
Дина |
Соня |
Коля |
Рома |
Миша |
|
|
Бойченко |
|
|
|
|
|
|
Карпенко Лысенко |
|
|
|
|
|
|
|
|
|
|
|
|
|
Савченко |
|
|
|
|
|
|
Шевченко |
|
|
|
|
|
Ответ: Дина Шевченко, Соня Бойченко, Коля Лысенко, Рома Савченко, Миша Карпенко.
Задача 51. Забывчивые друзья
Саша надумал навести порядок в своих книгах и обнаружил, что пяти книг не хватает: тома рассказов Марка Твена, книги «Энциклопедия профессора Фортрана», сборника сказок Андерсена, рассказов Бианки и сборника стихов Пушкина.
Саша смутно помнил, что кому-то давал эти книги. Но кому? Всего Саше удалось вспомнить следующее:
1) он давал книги только Андрею, Феде, Ире, Кате и Вале;
2) он всегда строго придерживался правила давать друзьям только по одной книге, причем следующую книгу давал только после того, как ему возвращали предыдущую;
 |
4) у Андрея две литературные привязанности: стихи Пушкина и рассказы Марка Твена, так что книги других авторов Андрей взять не мог;
5) Катя не любит читать ничего, кроме рассказов о животных;
6) Ира не читает ничего, кроме сказок и книг о компьютерах;
7) Валя — неизменный почитатель поэзии; всей остальной литературы для нее просто не существует. У кого какая книга находится?
Решение
По условию задачи имеем:
|
Название книги |
|
Имя |
|
||
|
Андрей |
Федя |
Ира |
Катя |
Валя |
|
|
Рассказы Марка Твена Энциклопедия профессора Фортрана |
|
|
О |
О |
о |
|
|
|
|
О |
о |
|
|
Рассказы Бианки Сборник стихов Пушкина |
|
|
О |
|
|
|
|
|
О |
о |
|
|
|
Сборник сказок Андерсена |
|
|
|
О |
о |
1. Так как Катя ничего не читает, кроме рассказов о животных, книга Виталия Бианки у нее — ведь это единственный из перечисленных авторов, который писал только о животных. Ставим в ячейку «Рассказы Бианки, Катя» цифру 1. В оставшуюся ячейку строки «Рассказы Бианки» ставим цифру О.
2.
 |
 |
|
Название книги |
|
Имя |
|
||
|
Андрей |
Федя |
Ира |
Катя |
Валя |
|
|
Рассказы Марка Твена |
|
|
о |
О |
о |
|
Энциклопедия профессора Фортрана |
|
|
|
О |
|
|
Рассказы Бианки |
|
о |
о |
1 |
|
|
Сборник стихов Пушкина |
|
О |
О |
о |
1 |
|
Сборник сказок Андерсена |
|
|
|
О |
о |
З. Из таблицы видно, что книга «Энциклопедия профессора Фортрана» у Иры. Ставим в ячейку «Энциклопедия профессора Фортрана, Ира» цифру 1 и в оставшуюся ячейку столбца «Ира» цифру О.
4. Так как у Андрея не сборник стихов Пушкина (по доказательству), у него рассказы Марка Твена (это следует из условия 4). Ставим в ячейку «Рассказы Марка Твена, Андрей» цифру 1. Следовательно, цифру 1 надо записать в ячейку «Сборник сказок Андерсена, Федя». В остальные ячейки ставим нули.
|
Название книги |
Имя |
|
|||
|
Андрей |
Федя |
Ира |
Катя |
Валя |
|
|
Рассказы Марка Твена |
1 |
о |
о |
о |
о |
|
Энциклопедия профессора Фортрана |
|
о |
1 |
о |
о |
|
Рассказы Бианки |
|
О |
о |
1 |
|
|
Сборник стихов Пушкина |
|
О |
о |
о |
1 |
|
Сборник сказок Андерсена |
О |
1 |
о |
о |
о |
Ответ: у Андрея — рассказы Марка Твена, у Феди — сборник
сказок Андерсена, у Иры 
«Энциклопедия профессора Фортрана» , у
Кати — рассказы Бианки, у Вали — сборник стихов Пушкина.
Задача 52. На конкурсе
Однажды на конкурсе за круглым столом оказалось пятеро ребят родом из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алеша, Коля и Витя.
Известно, что:
1)
 |
петербуржец сидел между Юрой и Толей, а напротив него сидели пермяк и
Алеша;
2) Коля никогда не был в Санкт-Петербурге; З) Юра не был в Москве и Томске;
4) томич с Толей регулярно переписываются.
Определите, в каком городе живет каждый из ребят. Решение
1. Петербуржец сидел между Юрой и Толей, напротив него сидел Алеша, а Коля никогда не был в Санкт-Петербурге (по условиям 1 и 2), значит, Алеша, Юра, Толя и Коля — не петербуржцы. Отсюда следует, что петербуржец — Витя. Ставим плюс в ячейку «Санкт-Петербург, Витя» и минусы в остальные ячейки строки «Санкт-Петербург» и столбца « Витя».
|
Город |
|
|
Имя |
|
|
|
Юра |
Толя |
Алеша |
Коля |
Витя |
|
|
Москва |
|
|
|
|
|
|
Санкт-Петербург |
|
|
|
|
|
|
Новгород |
|
|
|
|
|
|
Пермь |
|
|
|
|
|
|
Томск |
|
|
|
|
|
2.
 |
|
Город |
|
|
Имя |
|
|
|
юра |
Толя |
Алеша |
Коля |
Витя |
|
|
Москва |
|
|
|
|
|
|
Санкт-Петербург |
|
|
|
|
|
|
Новгород |
|
|
|
|
|
|
Пермь |
|
|
|
|
|
|
Томск |
|
|
|
|
|
З. Так как Юра не был в Москве и Томске (по условию З), а также не живет в Санкт-Петербурге и Перми (по доказательству), Юра — новгородец. Ставим в ячейку «Новгород, Юра» плюс, а во все остальные ячейки столбца «Юра» и строки «Новгород» минусы.
|
Город |
|
|
Имя |
|
|
|
юра |
Толя |
Алеша |
Коля |
Витя |
|
|
Москва |
|
|
|
|
|
|
Санкт-Петербург |
|
|
|
|
|
|
Новгород |
|
|
|
|
|
|
Пермь |
|
|
|
|
|
|
Томск |
|
|
|
|
|
4. Толя переписывается с томичем (по условию 4), значит, он не живет в Томске, а также не является жителем Санкт-Петербурга, Новгорода и Перми (по условию и по доказательству). Значит, Толя — москвич. Ставим плюс в ячейку «Москва, Толя», а все остальные ячейки столбца «Толя» и строки «Москва» заполняем минусами. Тогда из доказательства следует, что Алеша — томич. Ставим плюс в ячейку «Томск, Алеша».
|
Город |
|
|
Имя |
|
|
|
юра |
Толя |
Алеша |
Коля |
Витя |
|
|
Москва |
|
|
|
|
|
|
Санкт-Петербург |
|
|
|
|
|
|
Новгород |
|
|
|
|
|
|
Пермь |
|
|
|
|
|
|
Томск |
|
|
|
|
|
 |
Задача 53. Семья Семеновых
В семье Семеновых пять человек: муж, жена, их сын, сестра мужа и отец жены. Все они работают по профессиям: инженер, юрист, слесарь, экономист и учитель. Известно, что:
1) юрист и учитель — некровные родственники;
2) слесарь — хороший спортсмен. Он пошел по стопам экономиста и играет в футбол за сборную завода. Они оба мужчины;
З) инженер старше жены своего брата, но моложе, чем учитель.
Назовите профессию каждого члена семьи Семеновых. Решение
1. Брат есть только у одного члена семьи — у сестры мужа, а из условия З следует, что брат есть у инженера, значит, сестра мужа — инженер. Ставим плюс в ячейку «Сестра мужа, Инженер», а все остальные ячейки столбца «Инженер» и строки «Сестра мужа» заполняем минусами.
|
Степень родства |
|
Профессия |
|
||
|
Инженер |
Юрист |
Слесарь |
Экономист |
Учитель |
|
|
Муж |
|
|
|
|
|
|
Жена |
|
|
|
|
|
|
Сын |
|
|
|
|
|
|
Сестра мужа |
|
|
|
|
|
|
Отец жены |
|
|
|
|
|
2.
 |
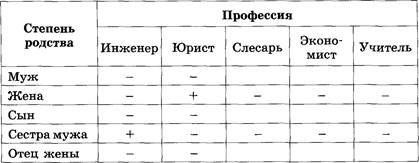
З. Юрист (жена, по доказательству) и
учитель 
некровные родственники (по условию 1),
значит, учитель — муж, так как с сыном и отцом жена находится в кровном
родстве. Ставим плюс в ячейку «Муж, Учитель», а все остальные ячейки столбца
«Учитель» и строки «Муж» заполняем минусами.
|
Степень родства |
|
Профессия |
|
||
|
Инженер |
Юрист |
Слесарь |
Экономист |
Учитель |
|
|
Муж |
|
|
|
|
|
|
Жена |
|
|
|
|
|
|
Сын |
|
|
|
|
|
|
Сестра мужа |
|
|
|
|
|
|
Отец жены |
|
|
|
|
|
 |
|
Степень родства |
|
Профессия |
|
||
|
Инженер |
Юрист |
Слесарь |
Эконо- МИСТ |
Учитель |
|
|
Муж |
|
|
|
|
|
|
Жена |
|
|
|
|
|
|
Сын |
|
|
|
|
|
|
Сестра мужа |
|
|
|
|
|
|
Отец жены |
|
|
|
|
|
Ответ: муж работает учителем, жена юристом, сын — слесарем, сестра мужа — инженером, отец жены — экономистом.
Задача 54. В небольшом городе
В небольшом районном городе живут пятеро
друзей: Иванов, Петренко, Сидорчук, Гришин и Капустин. Профессии у них разные:
один из них маляр, другой 
мельник, третий плотник, четвертый
почтальон, а пятый — парикмахер.
Известно, что:
1) Петренко и Гришин никогда не держали в руках малярной кисти;
2) Иванов
и Гришин уже давно собираются посетить мельницу, на которой работает их товарищ;
З) Петренко и Капустин живут в одном доме с почтальоном;
4) Сидорчук был недавно в загсе одним из свидетелей, когда Петренко и дочь парикмахера сочетались законным браком;
5) Иванов и Петренко каждое воскресенье играют в городки с плотником и маляром;
6) Гришин и Капустин по субботам обязательно встречаются в парикмахерской, где работает их друг, а почтальон предпочитает бриться сам.
Кто есть кто?
Решение
1.
 |
|
Фамилия |
Профессия |
||||
|
Маляр |
Мельник |
Плотник |
Почтальон |
Парикмахер |
|
|
Иванов |
|
|
|
|
|
|
Петренко |
|
|
|
|
|
|
Сидорчук |
|
|
|
|
|
|
Гришин |
|
|
|
|
|
|
Капустин |
|
|
|
|
|
2. Гришин тоже не держал в руках малярной кисти и ходит бриться в парикмахерскую в отличие от почтальона, который бреется сам (по условиям 1, 6). Значит, Гришин не маляр, не парикмахер и не почтальон (ставим минусы в ячейки на пересечении строки «Гришин» и столбцов «Маляр», «Парикмахер», «Почтальон») и не мельник (по доказательству). Следовательно, Гришин плотник. Ставим плюс в ячейку «Гришин, Плотник», а все остальные ячейки столбца «Плотник» заполняем минусами.
|
Фамилия |
Профессия |
||||
|
Маляр |
Мельник |
Плотник |
Почтальон |
Парикмахер |
|
|
Иванов |
|
|
|
|
|
|
Петренко |
|
|
|
|
|
|
Сидорчук |
|
|
|
|
|
|
Гришин |
|
|
|
|
|
|
Капустин |
|
|
|
|
|
 |
|
Фамилия |
Профессия |
||||
|
Маляр |
Мельник |
Плотник |
Почтальон Парикмахер |
||
|
Иванов |
|
|
|
|
|
|
Петренко |
|
|
|
|
|
|
Сидорчук |
|
|
|
|
|
|
Гришин |
|
|
|
|
|
|
Капустин |
|
|
|
|
|
4. Сидорчук был
свидетелем на свадьбе дочери парикмахера (по условию 4), значит, он не
парикмахер. Ставим минус в ячейку «Сидорчук, Парикмахер» . Сидорчук также не
мельник, не плотник и не маляр (по доказательству). Значит, Сидорчук 
почтальон.
Ставим плюс в ячейку «Сидорчук, Почтальон» и минусы в остальные ячейки столбца
«Почтальон». Получаем, что Иванов парикмахер. Ставим плюс в соответствующую
ячейку.
|
Фамилия |
Профессия |
||||
|
Маляр |
Мельник |
Плотник |
Почтальон Парикмахер |
||
|
Иванов |
|
|
|
|
|
|
Петренко |
|
|
|
|
|
|
Сидорчук |
|
|
|
|
|
|
Гришин |
|
|
|
|
|
|
Капустин |
+ |
|
|
|
|
Ответ: Иванов парикмахер, Петренко мельник, Сидорчук почтальон,
Гришин 
плотник, Капустин — маляр.
Задача 55. Удочки
 |
решили купить себе
удочки. Удочки были пяти цветов: красного, синего, белого, зеленого и черного.
Известно, что:
1) Дима любит красный и синий цвета;
2) Сереже нравились синяя и зеленая удочки;
З) Коля купил зеленую удочку;
4) Юра отдавал предпочтение красной, синей и черной удочкам.
Кто какую удочку купил, если у всех были удочки разного цвета?
Решение
Составим таблицу и будем ставить в ячейку 1, если утверждение истинно, и О, если оно ложно.
1. Дима купил или красную, или синюю удочку (по условию 1). В столбцы, не соответствующие этим цветам, ставим нули. Аналогичное рассуждение относится к Сереже и Юре. Коля купил зеленую удочку (по условию З). В ячейку «Коля, Зеленый» ставим 1, а в остальные ячейки столбца «Зеленый» и строки «Коля» ставим нули.
|
Имя |
|
Цвет удочки |
|
||
|
Синий |
Красный |
Черный |
Белый |
Зеленый |
|
|
Дима |
|
|
|
|
|
|
Саша |
|
|
|
|
|
|
Коля |
|
|
|
|
1 |
|
Сережа |
|
|
|
|
|
|
юра |
|
|
|
|
|
2.
 |
|
Имя |
|
Цвет удочки |
|
||
|
Синий |
Красный |
Черный |
Белый |
Зеленый |
|
|
Дима |
|
1 |
|
О |
|
|
Саша |
|
|
|
1 |
|
|
Коля |
|
|
|
|
1 |
|
Сережа |
1 |
|
|
|
|
|
Юра |
|
|
1 |
|
|
Ответ: Дима купил красную удочку, Саша белую, Коля зеленую, Сережа синюю, Юра — черную.
Задача 56. Профессии
В одном небольшом кафе в смене одновременно работали пять человек: администратор, повар, кондитер, кассир и дворник. Одновременно на работу выходили мисс Галбрэйт, мисс Шерман, мистер Вильямс, мистер Вортман и мистер Блэйк. При этом было известно, что:
1) повар — холостяк;
2) кассир и администратор жили в одной комнате, когда учились в колледже;
З) мистер Блэйк и мисс Шерман встречаются только на работе;
4) миссис Вильямс была очень недовольна, когда муж сказал ей, что администратор отказал ему в отгуле на субботний вечер;
5) Вортман собирается быть шафером на свадьбе у кассира и кондитера.
Кто на какой должности в этом кафе?
Решение
1.
 |
|
Должность |
Сотрудник |
||||
|
Мисс Галбрэйт |
Мисс Шерман |
Мистер Вильямс |
Мистер Вортман |
Мистер Блэйк |
|
|
Администратор |
|
|
|
|
|
|
Повар |
|
|
|
|
|
|
Кондитер |
|
|
|
|
|
|
Кассир |
|
|
|
|
|
|
Дворник |
|
|
|
|
|
2. Так как повар и дворник — мужчины, из условия 2 следует, что кассир и администратор — женщины, а кондитер — мужчина. Ставим минусы в ячейки на пересечении строк «Кондитер» и «Повар» и столбцов «Мисс Галбрэйт», «Мисс Шерман», а также в ячейки на пересечении строк «Кассир», «Администратор» и столбцов «Мистер Вортман» , «Мистер Блэйк».
|
Должность |
Сотрудник |
||||
|
Мисс Галбрэйт |
Мисс Шерман |
Мистер Вильямс |
Мистер Вортман |
Мистер Блэйк |
|
|
Администратор |
|
|
|
|
|
|
Повар |
|
|
|
|
|
|
Кондитер |
|
|
|
|
|
|
Кассир |
|
|
|
|
|
|
Дворник |
|
|
|
|
|
 |
|
Должность |
Сотрудник |
||||
|
Мисс Галбрэйт |
Мисс Шерман |
Мистер Вильямс |
Мистер Вортман |
Мистер Блэйк |
|
|
Администратор |
|
|
|
|
|
|
Повар |
|
|
|
|
|
|
Кондитер |
|
|
|
|
|
|
Кассир |
|
|
|
|
|
|
Дворник |
|
|
|
|
|
4. Из таблицы видно, что повар — это мистер Вортман. Ставим плюс в ячейку «Повар, Мистер Вортман» .
|
Должность |
Сотрудник |
||||
|
Мисс Галбрэйт |
Мисс Шерман |
Мистер Вильямс |
Мистер Вортман |
Мистер Блэйк |
|
|
Администратор |
|
|
|
|
|
|
Повар |
|
|
|
|
|
|
Кондитер |
|
|
|
|
|
|
Кассир |
|
|
|
|
|
|
Дворник |
|
|
|
|
|
5. Кондитер мистер Блэйк женится на кассире, а с мисс Шерман он встречается только на работе (по условиям З и 5), значит, кассир — мисс Галбрэйт, а мисс Шерман — администратор. Ставим плюсы в ячейки «Кассир, Мисс Галбрэйт» и «Администратор, Мисс Шерман» и минусы — в остальные ячейки.
|
Должность |
Сотрудник |
||||
|
Мисс Галбрэйт |
Мисс Шерман |
Мистер Вильямс |
Мистер Вортман |
Мистер Блэйк |
|
|
Администратор |
|
|
|
|
|
|
Повар |
|
|
|
|
|
|
Кондитер |
|
|
|
|
|
|
Кассир |
|
|
|
|
|
|
Дворник |
|
|
|
|
|
Ответ: мисс Галбрэйт кассир, мисс
Шерман 
администратор, мистер Вильямс — дворник,
мистер Вортман — повар, мистер Блэйк 
кондитер.
 |
Живут-поживают пять зайчат: Прыгунчик, Ушастик, Тишка, Зайка и Беляк, и у каждого есть мячик. Цвета мячиков такие: синий, зеленый, красный, желтый и оранжевый. У Ушастика мячик желтого цвета, а у Зайки — не зеленый, не синий и не красный. У Прыгунчика был бы синий мячик, если бы у Беляка был зеленый мячик, но у Беляка мячик другого цвета. Беляк не любит игрушки синего цвета. У кого какой мячик?
Решение
1. У Ушастика желтый мячик (по условию). Ставим плюс в ячейку «Желтый, Ушастик», а все остальные ячейки столбца «Ушастик» и строки «Желтый» заполняем минусами. У Зайки не зеленый, не синий и не красный мячик (по условию). Ставим минусы в ячейки на пересечении столбца «Зайка» и строк «Синий», «Красный», «Зеленый». Значит, у Зайки оранжевый мячик. Ставим плюс в ячейку «Оранжевый, Зайка», а все остальные ячейки строки «Оранжевый» заполняем минусами.
|
Цвет мячика |
|
Кличка зайчика |
|
||
|
Прыгунчик |
Ушастик |
Тишка |
Зайка |
Беляк |
|
|
Зеленый |
|
|
|
|
|
|
Синий |
|
|
|
|
|
|
Красный |
|
|
|
|
|
|
Желтый |
|
|
|
|
|
|
Оранжевый |
|
|
|
|
|
2. У Беляка не зеленый и не синий мячик (по условию)
 |
|
Цвет мячика |
|
Кличка зайчика |
|
||
|
Прыгунчик |
Ушастик |
Тишка |
Зайка |
Беляк |
|
|
Зеленый |
|
|
|
|
|
|
Синий |
|
|
|
|
|
|
Красный |
|
|
|
|
|
|
Желтый |
|
|
|
|
|
|
Оранжевый |
|
|
|
|
|
З. У Прыгунчика не синий мячик (это следует из условия) (ставим минус в ячейку «Синий, Прыгунчик») и не красный, не желтый, не оранжевый (по доказательству), значит, у Прыгунчика зеленый мячик. Тогда получаем, что синий мячик — у Тишки. Ставим плюсы в ячейки «Зеленый, Прыгунчик», «Синий, Тишка» и минусы в оставшиеся ячейки.
|
Цвет мячика |
|
Кличка зайчика |
|
||
|
Прыгунчик |
Ушастик |
Тишка |
Зайка |
Беляк |
|
|
Зеленый |
|
|
|
|
|
|
Синий |
|
|
|
|
|
|
Красный |
|
|
|
|
|
|
Желтый |
|
|
|
|
|
|
Оранжевый |
|
|
|
|
|
Ответ: у Прыгунчика — зеленый мячик, у Ушастика — желтый, у
Тишки — синий, у Зайки 
оранжевый, у Беляка — красный.
Задача 58. Машины
 |
Решение
1. У
Джека красная машина (по условию) (ставим плюс в ячейку «Красная, Джек» и
минусы 
в остальные ячейки столбца «Джек» и строки
«Красная»), а у Питера — не черная, не синяя и не голубая машина (по условию)
(ставим минусы в ячейки на пересечении столбца «Питер» и строк «Синяя»,
«Голубая», «Черная»), значит, у Питера — белая машина. Ставим плюс в ячейку
«Белая, Питер», а все остальные ячейки строки «Белая» и столбца «Питер» заполняем
минусами.
|
Цвет машины |
|
|
Гонщик |
|
|
|
Джек |
Питер |
Майк |
Алексей |
Берри |
|
|
Красная |
|
|
|
|
|
|
Черная |
|
|
|
|
|
|
Синяя |
|
|
|
|
|
|
Голубая |
|
|
|
|
|
|
Белая |
|
|
|
|
|
2. У Берри есть белая и синяя машины (по условию), но на белой машине приехал Питер (по доказательству). Значит, Берри приехал на синей машине. Ставим плюс в ячейку «Синяя, Берри», а все остальные ячейки строки «Синяя» и столбца «Берри» заполняем минусами.
|
Цвет машины |
|
|
Гонщик |
|
|
|
Джек |
Питер |
Майк |
Алексей |
Берри |
|
|
Красная |
|
|
|
|
|
|
Черная |
|
|
|
|
|
|
Синяя |
|
|
|
|
|
|
Голубая |
|
|
|
|
|
|
Белая |
|
|
|
|
|
 |
|
Цвет машины |
|
|
Гонщик |
|
|
|
Джек |
Питер |
Майк |
Алексей |
Берри |
|
|
Красная |
|
|
|
|
|
|
Черная |
|
|
|
|
|
|
Синяя |
|
|
|
|
|
|
Голубая |
|
|
|
|
|
|
Белая |
|
|
|
|
|
Ответ: у Джека — красная машина, у Питера — белая, у Майка — черная, у Алексея — голубая, у Берри — синяя.
Задача 59. Выпускники
 |
А актер, врач и банкир оказались целиком правы. Установите, кто из них какую профессию выбрал. Решение
1. Ошиблись в суждениях метрдотель и учитель, а Виктор хотел стать метрдотелем (по условию), следовательно, он не стал метрдотелем (иначе утверждение метрдотеля было бы истинно). Значит, он ошибался, а кроме метродотеля ошибался только учитель (по условию). Значит, Виктор стал учителем. Ставим плюс в ячейку «Учитель, Виктор» и минусы в остальные ячейки строки «Учитель» и столбца «Виктор» .
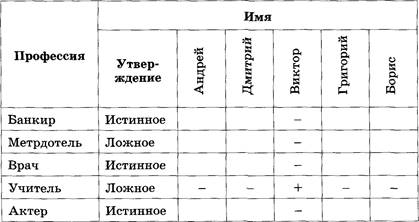
2.
 |
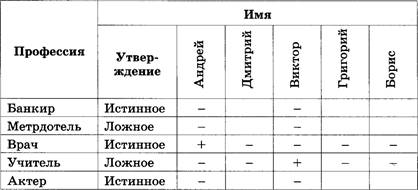
З. Григорий утверждал, что Андрей не будет врачом (по условию), а Андрей стал врачом (по доказательству), значит, Григорий ошибался. А ошибались (по условию) учитель (Виктор, по доказательству) и метрдотель. Следовательно, Григорий стал метрдотелем. Ставим плюс в ячейку «Метрдотель, Григорий» и минусы в остальные ячейки строки «Метрдотель» и столбца «Григорий» .
|
Профессия |
Имя |
|
||||
|
Утверждение |
|
|
|
2-4
|
2-4
|
|
|
Банкир |
Истинное |
|
|
|
|
|
|
Метрдотель |
Ложное |
|
|
|
|
|
|
Врач |
Истинное |
|
|
|
|
|
|
Учитель |
Ложное |
|
|
|
|
|
|
Актер |
Истинное |
|
|
|
|
|
4. Андрей утверждал, что Дмитрий не будет банкиром (по условию), и притом Андрей не ошибался, так как он врач (по доказательству), следовательно, Дмитрий — не банкир, а актер. Получаем, что банкир — Борис. Заполняем оставшиеся ячейки.
|
Профессия |
Имя |
|||||
|
Утверждение |
|
|
|
|
|
|
|
Банкир |
Истинное |
|
|
|
|
|
|
Метрдотель |
Ложное |
|
|
|
|
|
|
Врач |
Истинное |
|
|
|
|
|
|
Учитель |
Ложное |
|
|
|
|
|
|
Актер |
Истинное |
|
|
|
|
|
 |
Задача 60. На шахматном турнире
В шахматном турнире принимали участие шесть партнеров разных профессий: токарь, слесарь, инженер, учитель, врач и шофер.
Известно, что:
1) в
первом туре Андреев играл с врачом, учитель 
с Борисовым, а
Григорьев — с Евдокимовым; в первом туре З партии;
2) во втором туре Дмитриев играл с токарем, а врач — с Борисовым; во втором туре 2 партии;
З) в третьем туре Евдокимов играл с инженером; в третьем туре 1 партия; тем временем токарь обсуждал с учителем ход игры во втором туре;
4) по окончании турнира места распределились так: Борисову присудили 1-е место, Григорьев и инженер поделили 2-е и 3-е места, Дмитриев занял 4-е место, а Золотарев и слесарь поделили 5-е и 6-е места.
У кого какая профессия?
Решение
1. В первом туре З партии (по условию 1), значит, врач — не Андреев, не Борисов, не Григорьев, не Евдокимов. Ставим минусы в ячейки на пересечении столбца «Врач» и строк «Андреев», «Борисов» , «Григорьев», «Евдокимов».
|
Фамилия |
Профессия |
|||||
|
Токарь |
Слесарь |
Инженер |
Учитель |
Врач |
Шофер |
|
|
Андреев |
|
|
|
|
|
|
|
Борисов |
|
|
|
|
|
|
|
Дмитриев |
|
|
|
|
|
|
|
Григорьев |
|
|
|
|
|
|
|
Евдокимов |
|
|
|
|
|
|
|
Золотарев |
|
|
|
|
|
|
 |
|
Фамилия |
Профессия |
|||||
|
Токарь |
Слесарь |
Инженер |
Учитель |
Врач |
Шофер |
|
|
Андреев |
|
|
|
|
|
|
|
Борисов |
|
|
|
|
|
|
|
Дмитриев |
|
|
|
|
|
|
|
Григорьев |
|
|
|
|
|
|
|
Евдокимов |
|
|
|
|
|
|
|
Золотарев |
|
|
|
|
|
|
З. Учитель — не
Андреев, не Борисов, не Григорьев, не Евдокимов (по условию 1) (ставим минусы в
ячейки на пересечении столбца «Учитель» и строк «Андреев», «Борисов»,
«Григорьев», «Евдокимов») и не 30лотарев (по доказательству), значит, учитель 
Дмитриев.
Ставим плюс в ячейку «Дмитриев, Учитель», все остальные ячейки строки
«Дмитриев» заполняем минусами.
|
Фамилия |
Профессия |
|||||
|
Токарь |
Слесарь |
Инженер |
Учитель |
Врач |
Шофер |
|
|
Андреев |
|
|
|
|
|
|
|
Борисов |
|
|
|
|
|
|
|
Дмитриев |
|
|
|
|
|
|
|
Григорьев |
|
|
|
|
|
|
|
Евдокимов |
|
|
|
|
|
|
|
Золотарев |
|
|
|
|
|
|
4.
 |
|
Фамилия |
Профессия |
|||||
|
Токарь |
Слесарь |
Инженер |
Учитель |
Врач |
Шофер |
|
|
Андреев |
|
|
|
|
|
|
|
Борисов |
|
|
|
|
|
|
|
Дмитриев |
|
|
|
|
|
|
|
Григорьев |
|
|
|
|
|
|
|
Евдокимов |
|
|
|
|
|
|
|
Золотарев |
|
|
|
|||
5. Токарь — не Борисов (по условию 2), не Евдокимов (по условию З), не Золотарев и не Дмитриев (по доказательству), значит, токарь — Григорьев (по условию 4). Ставим плюс в ячейку «Григорьев, Токарь», а оставшиеся ячейки строки «Григорьев» и столбца «Токарь» заполняем минусами.
|
Фамилия |
Профессия |
|
||||
|
Токарь |
Слесарь |
Инженер |
Учитель |
Врач |
Шофер |
|
|
Андреев |
|
|
|
|
|
|
|
Борисов |
|
|
|
|
|
|
|
Дмитриев |
|
|
|
|
|
|
|
Григорьев |
|
|
|
|
|
|
|
Евдокимов |
|
|
|
|
|
|
|
Золотарев |
|
|
|
|
|
|
6.
 |
|
Фамилия |
Профессия |
|
||||
|
Токарь |
Слесарь |
Инженер |
Учитель |
Врач |
Шофер |
|
|
Андреев |
|
|
|
|
|
|
|
Борисов |
|
|
|
|
|
|
|
Дмитриев |
|
|
|
|
|
|
|
Григорьев |
|
|
|
|
|
|
|
Евдокимов |
|
|
|
|
|
|
|
Золотарев |
|
|
|
|
|
|
Ответ: токарь — Григорьев, слесарь — Евдокимов, инженер — Андреев, учитель — Дмитриев, врач — Золотарев, шофер — Борисов.
Задача 61. Преподаватели
В педагогическом институте Аркадьева, Бабанова, Корсакова, Дашков, Ильин и Флеров преподают экономическую географию, английский язык, немецкий язык, историю, французский язык и математику.
Известно, что:
1) преподаватель немецкого языка и преподаватель математики в студенческие годы занимались художественной гимнастикой;
2) Ильин старше Флерова, но стаж работы у него меньше, чем у преподавателя экономической географии;
З) будучи студентками, Аркадьева и Бабанова учились вместе в одном университете. Все остальные окончили педагогический институт;
4) Флеров — сын преподавателя французского языка, но студентом у него не был;
5)
 |
6) Аркадьева старше преподавателя немецкого языка. Кто какой предмет преподает?
Решение
1. Преподаватели немецкого языка и математики занимались художественной гимнастикой (по условию 1), следовательно, они женщины. Ставим минусы в ячейки на пересечении строк «Немецкий язык», «Математика» и столбцов «Дашков», «Ильин», «Флеров».
|
Учебный предмет |
Фамилия |
|||||
|
|
|
|
|
|
|
|
|
Эконом. география |
|
|
|
|
|
|
|
Английский язык |
|
|
|
|
|
|
|
Немецкий язык |
|
|
|
|
|
|
|
История |
|
|
|
|
|
|
|
Французский язык |
|
|
|
|
|
|
|
Математика |
|
|
|
|
|
|
2.
 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Эконом. география |
|
|
|
|
|
|
|
Английский язык |
|
|
|
|
|
|
|
Немецкий язык |
|
|
|
|
|
|
|
История |
|
|
|
|
|
|
|
Французский язык |
|
|
|
|
|
|
|
Математика |
|
|
|
|
|
|
З. Из таблицы видно, что математику преподает Корсакова. Ставим плюс в ячейку «Математика, Корсакова», а все остальные ячейки столбца «Корсакова» заполняем минусами.
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Эконом. география |
|
|
|
|
|
|
|
Английский язык |
|
|
|
|
|
|
|
Немецкий язык |
|
|
|
|
|
|
|
История |
|
|
|
|
|
|
|
Французский язык |
|
|
|
|
|
|
|
Математика |
|
|
|
|
|
|
4.
 |
5. Учитель французского языка самый старший по возрасту и по стажу работы (по условию 5), значит, это не Ильин, не Флеров (по условию 2). Ставим минусы в ячейки «Французский язык, Ильин» , «Французский язык, Флеров». Значит, это Дашков. Ставим плюс в ячейку «Французский язык, Дашков», а все остальные ячейки столбца «Дашков» заполняем минусами.
6.
 |
— сын учителя французского языка,
но студентом у него не был (по условию 4), значит, он не преподает историю (по
условию 5). Следовательно, он преподаватель английского языка. Ставим плюс в
ячейку «Английский язык, Флеров» и минус в оставшуюся ячейку столбца «Флеров».
Получаем, что учитель истории — Ильин. Ставим плюс в ячейку «История, Ильин» и
минус в оставшуюся ячейку столбца «Ильин» .
Ответ: Аркадьева преподает экономическую географию, Бабанова — немецкий язык, Дашков — французский язык, Ильин — историю, Корсакова математику, Флеров английский язык.
Задача 62. Финал турнира Российской армии
В финале турнира шахматистов Российской армии встретились представители восьми воинских званий: полковник, майор, капитан, лейтенант, старшина, сержант, ефрейтор и солдат. Все — из разных родов войск: пехотинец, летчик, танкист, артиллерист, кавалерист, минометчик, сапер и связист.
Рассуждая правильно, вы сможете определить воинскую специальность каждого из 8 шахматистов по следующим данным:
1) в 1-м туре полковник играл с кавалеристом, а майор — с танкистом. Летчик приехал только ко второму туру;
2)
 |
З) в 3-м туре лейтенант выиграл у пехотинца, партия полковника с артиллеристом окончилась вничью, а минометчик выиграл у ефрейтора;
4) в 4-м туре сапер выиграл у лейтенанта, а старшина — у полковника.
Указание. Для решения этой задачи не требуется умения играть в шахматы. Следует только знать, что в турнире один и тот же шахматист два раза выходным не бывает и с каждым партнером играет по одной партии.
Ответ: солдат пехотинец, летчик капитан, танкист — ефрейтор,
артиллерист — майор, кавалерист лейтенант, минометчик 
старшина,
сапер — сержант, связист — полковник.
4-1703
Задача 63. Симфонический оркестр
В симфонический оркестр приняли на работу трех музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
1) Смит самый высокий;
2) играющий на скрипке меньше ростом, чем играющий на флейте;
З) играющие на скрипке и флейте и Браун любят пиццу;
4) когда между альтистом и трубачом возникает ссора, Смит мирит их;
5) Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение
1.
 |
2. Браун не умеет играть на скрипке, флейте, трубе и гобое (это следует из условий З и 5). Следовательно, инструменты Брауна — альт и кларнет. Ставим единицы и нули в нужные ячейки строки «Браун», а оставшиеся ячейки столбцов «Альт» и «Кларнет» заполняем нулями. Смит также не играет на трубе (это следует из условия 4). Ставим «О» в ячейку «Смит, Труба».
|
Музыкант |
Музыкальный инструмент |
|
||||
|
Скрипка |
Флейта |
Альт |
Кларнет |
Гобой |
Труба |
|
|
Браун |
|
|
1 |
1 |
|
|
|
Смит |
|
|
|
|
|
|
|
Вессон |
|
|
О |
о |
|
|
З. Из таблицы видно, что на трубе может играть только Вессон. Ставим 1 в ячейку «Вессон, Труба» . Смит — не скрипач (это следует из условий 1 и 2). Ставим «О» в ячейку «Смит, Скрипка». На скрипке
не играет ни Браун, ни Смит, значит, скрипачом является Вессон. Ставим «1» в ячейку «Вессон, Скрипка» . Оба инструмента, на которых играет Вессон, теперь определены. Поэтому остальные ячейки строки «Вессон» можно заполнить нулями.
|
Музыкант |
Музыкальный инструмент |
|
||||
|
Скрипка |
Флейта |
Альт |
Кларнет |
Гобой |
Труба |
|
|
Браун |
о |
|
1 |
1 |
|
|
|
Смит |
|
|
о |
о |
|
|
|
Вессон |
1 |
О |
О |
|
|
1 |
 |
|
Музыкант |
Музыкальный инструмент |
|
||||
|
Скрипка |
Флейта |
Альт |
Кларнет |
Гобой |
Труба |
|
|
Браун |
|
о |
1 |
1 |
|
|
|
Смит |
|
1 |
О |
О |
1 |
|
|
Вессон |
1 |
|
О |
О |
|
1 |
Ответ: Браун играет на альте и
кларнете, Смит 
на флейте и гобое, Вессон на скрипке и
трубе.
Задача 64. Внучка
— Мои четыре внучки — замечательные
девочки, 
рассказывала бабушка Пелагея с
нескрываемой гордостью. Каждая из них играет на каком-нибудь музыкальном
инструменте и говорит на одном из иностранных языков.
— На чем играет Маша? — спросила я.
— На рояле.
— А кто играет на скрипке?
— Помню только, что это та девочка, которая говорит по-французски, — ответила бабушка.
Поговорив с бабушкой, я также узнала, что Оля играет на виолончели, а Лена не говорит по-немецки. Маша не знает итальянского языка, а Оля не владеет английским. Валя не знает французского, Лена не играет на арфе, а виолончелистка не говорит по-итальянски. Я совсем запуталась. Скажите мне, кто на каком инструменте играет и на каком языке говорит.
Решение
1. На арфе играет не Маша (она по условию играет на рояле), не Оля (она по условию играет на виолончели) и не Лена (по условию), значит, на арфе играет Валя, а Лена играет на скрипке. Ставим плюсы в ячейки «Валя, Арфа», «Лена, Скрипка», «Маша, Рояль», «Оля, Виолончель» и минусы в остальные ячейки левой части таблицы.
2.
 |
З. Оля не говорит по-английски (по условию). Она играет на виолончели (по условию), следовательно, не говорит по-итальянски. Оля также не говорит по-французски, так как по-французски говорит Лена. Значит, Оля говорит по-немецки. Ставим плюс в ячейку «Оля, Нем. яз.» и минусы в соответствующие ячейки правой части таблицы.
4. Маша не говорит по-итальянски (по
условию), по-французски и по-немецки (по доказательству), значит, она говорит
по-английски, а Валя 
по-итальянски (ставим плюсы и минусы в
нужные ячейки).
|
Имя |
Музыкальный инструмент |
Язык |
||||||
|
|
|
|
|
|
со
|
|
|
|
|
Маша |
|
|
|
|
|
|
|
|
|
Оля |
|
|
|
|
|
|
|
|
|
Лена |
|
|
|
|
|
|
|
|
|
Валя |
|
|
|
|
|
|
|
|
Ответ: Маша играет на рояле и изучает английский язык, Оля играет на виолончели и изучает немецкий язык, Лена играет на скрипке и изучает французкий язык, Валя играет на арфе и изучает итальянский язык.
Задача 65. На званом вечере
На одном званом вечере среди гостей оказалось пять офицеров: пехотинец, артиллерист, летчик, связист и сапер. Один из них капитан, трое майоры и один — полковник. Дамы окружили офицеров таким вниманием, что все остальные гости оказались просто забытыми.
Из разговора удалось выяснить следующее:
1)у Петра такое же звание, как и у его друга сапера;
2)офицер-связист и Николай — большие друзья;
З) офицер-летчик вместе с Владимиром и Александром недавно были в гостях у Николая;
4)
 |
5) Николай чуть было не стал летчиком, но потом по совету своего друга сапера избрал иной род войск;
6) Петр по званию старше Александра, Владимир по званию старше Николая.
Определите звание каждого офицера и род войск, в котором он служит.
Решение
1.
Александр не артиллерист, не сапер, не связист, не летчик (это следует
из условий З, 4), значит, он 
пехотинец. Ставим в ячейку «Александр,
Пехотинец» плюс, а в остальные соответствующие ячейки левой части таблицы —
минусы.
2. Николай не летчик, не сапер, не связист (это следует из условий 2, 5) и не пехотинец (по доказательству), значит, он — артиллерист. Ставим в ячейку «Николай, Артиллерист» плюс, а в остальные соответствующие ячейки левой части таблицы — минусы.
З. Из условия 1 следует, что Петр может быть только майором: только майоров, по условию задачи, несколько. Ставим плюс в ячейку «Петр, Майор» . Петр (майор) по званию старше Александра (по условию 6), значит, Александр капитан. Ставим в ячейку «Александр, Капитан» плюс, а в остальные соответствующие ячейки правой части таблицы минусы.
4.
 |
5. Остается, что Андрей — майор. Ставим плюс в ячейку «Андрей, Майор» .
6. Сапер — майор, но не Петр (это следует из условия 1), не Николай и не Александр (по доказательству) и не Владимир (который, по доказательству, полковник), значит, сапер — Андрей. Ставим в ячейку «Андрей, Сапер» плюс, а в остальные соответствующие ячейки минусы.
7. Из условия З следует, что Владимир не летчик, Значит, он связист, а Петр летчик. Ставим плюсы в ячейки «Владимир, Связист» и «Петр, Летчик», а в остальные соответствующие ячейки минусы.
Ответ: Петр — летчик, майор; Николай — артиллерист, майор; Владимир связист, полковник; Александр пехотинец, капитан; Андрей — сапер, майор.
Задача 66. Коробочки
— Ой, какие красивые разноцветные шарики! А какие коробочки! Дедушка, ну пожалуйста, подари мне их! — воскликнула Леночка, едва переступив порог дедушкиной комнаты.
Посмотрим,
заслуживаешь ли ты такого подарка, — ответил дедушка и попросил Леночку на некоторое
время выйти из комнаты. Но не прошло и минуты, как девочка услышала, что ее уже
зовут.
 |
Перед
тобой пять коробочек: одна белая, одна красная, одна синяя, одна черная и одна
зеленая, 
сказал дедушка. — Шарики тех же цветов,
что и коробочки, по два шарика каждого цвета: два белых, два черных, два синих,
два красных и два зеленых. В каждую коробочку я положил по два шарика. Чтобы ты
не думала, будто цвет шариков в коробочке совпадает с цветом самой коробочки,
скажу сразу: шарики по коробочкам я разложил как пришлось. Если ты скажешь,
какого цвета шарики лежат в каждой коробочке, то я подарю тебе все шарики
вместе с коробочками.
— Но ведь это очень трудно, — печально вздохнула Леночка.
— Совсем не трудно, — утешил дедушка. — Я помогу тебе — вот слушай:
1) ни один шарик не лежит в коробочке того цвета, что и он сам;
2) в красной коробочке нет синих шариков;
З) в черной коробочке лежит по одному шарику каждого из холодных тонов (Леночка уже знала, что холодными называются зеленый и синий тона);
4) в одной из коробочек нейтрального цвета лежат один красный и один зеленый шарик (Леночка, не выдержав, спросила, что такое нейтральный цвет. Дедушка ответил, что так принято называть белый или черный цвет);
5) в синей коробочке находится один черный шарик;
6) в одной из коробочек лежат один белый и один синий шарики.
Помогите Леночке решить задачу.
Решение
1. В черной коробочке лежат синий и зеленый шарики (это следует из условия З).
2. Коробочка нейтрального цвета — черная или белая. Но содержимое черной коробочки уже определено, значит, речь идет о белой коробочке. В ней — красный и зеленый шарики (это следует из условия 4).
 |
4. В красной коробочке не могут лежать красные шарики, синие шарики (по условию 2), зеленые шарики (они уже разложены в черную и белую коробочки). Значит, в ней — белый и черный шарики.
5. Остается синяя коробочка в ней лежат оставшиеся красный и черный шарики. Окончательно получим:
|
цвет коробочки |
|
Цвет шариков |
|
|||||||
|
Красный |
Белый |
Синий |
Черный |
Зеленый |
||||||
|
Красный |
|
|
|
|
|
|
|
|
|
|
|
Белый |
|
|
|
|
|
|
|
|
|
|
|
Синий |
|
|
|
|
|
|
|
|
|
|
|
Черный |
|
|
|
|
|
|
|
|
|
|
|
Зеленый |
|
|
|
|
|
|
|
|
|
|
Ответ: см. таблицу.
Разнообразие задач и способов их решения часто представляется «океаном», в котором только случай может помочь маленькому беззащитному пловцу найти правильный курс. Между тем, есть надежный «компас» и другие надежные инструменты решения логических задач, которые помогут преодолеть все препятствия каждому, кто научится ими пользоваться.
Далее предлагаются задачи, в которых имеются не два набора элементов, между которыми требуется установить соответствие объединить их в пары, а три набора, т. е. элементы объединяются в тройки, устанавливается соответствие между каждым элементом основного набора (относительно которого решается задача) и двумя элементами двух других наборов. Такие задачи решаются с использованием схем (задачи, где не более трех основных элементов) и в основном таблиц (задачи, где более трех основных элементов).
Задача 67. Костюмы и шапочки
У трех подружек — Ксюши, Насти и Оли — новогодние карнавальные костюмы белого, синего и фиолетового цветов и шапочки тех же цветов. У Насти цвета костюма и шапочки совпадают, у Ксюши ни костюм, ни шапочка не фиолетового цвета, а Оля в белой шапочке, но цвет костюма у нее не такой же. Как одеты девочки?
Решение
1. У Ксюши костюм и шапочка не фиолетовые (по условию) и шапочка не белого цвета (так как белая шапочка у Оли), значит, шапочка у нее синяя. Проводим сплошную линию между именем Ксюша и переменной С (в разделе «шапочки») и пунктирные линии — между «Ксюша» и «Ф» (костюмы), «Ксюша» и «Ф» (шапочки), «Ксюша» и «Б» (шапочки).
Б ш
п
Ксюша О
и Настя к о с
Олят
м ы
2. Шапочка у
Насти не синяя (по доказательству) и не белая (так как белая шапочка у Оли).
Значит, у нее фиолетовая шапочка и такой же костюм (по условию). Проводим
сплошную линию между «На
и «Ф» (шапочки), «Настя» и «Ф» (костюмы) и
пунктирные линии между«Настя» и «С» (шапочки), «Настя» и «Б» (шапочки).
З. Костюм у Оли не фиолетовый (по доказательству) и не белый (по условию), значит, он синий. Проводим сплошную линию между «Оля» и «С» (костюмы) и пунктирные линии между «Оля» и «Ф» (костюмы), «Оля» и «Б» (костюмы). У Оли белая шапочка (по условию). Проводим сплошную линию между «Оля» и «Б» (шапочки).
4. У Оли синий костюм, у Насти — фиолетовый (по доказательству). Значит, у Ксюши белый костюм. Проводим сплошную линию между «Ксюша» и «Б» (костюмы).
 |
Задача 68. Щенки
Три друга — Алеша,
Сережа и Денис — купили щенков разной породы — колли, ротвейлера и овчарку 
и
дали им клички Лесси, Джек и Гриф. Известно, что щенок Алеши темнее по окрасу,
чем овчарка, Лесси и Джек; щенок Сережи старше Джека, ротвейлера и овчарки.
Какой породы щенок и с какой кличкой у каждого из ребят?
Решение
1. Из условия задачи следует, что у Алеши не овчарка, не Лесси и не Джек; у Сережи не Джек, не ротвейлер и не овчарка. Отметим эти выводы на схеме пунктирными линиями.
2. Из схемы видно, что у Сережи колли, значит, овчарка у Дениса. Следовательно, у Алеши ротвейлер. Также из схемы получаем, что Джек — кличка собаки Дениса, а кличка собаки Алеши — Гриф. Значит, у Сережи — собака по кличке Лесси. Отметим эти выводы на схеме сплошными линиями.
колли
ротвейлер
овчарка
Ответ: у Дениса овчарка по кличке Джек, у Сережи колли по кличке Лесси, у Алеши ротвейлер по кличке Гриф.
Задача 69. Украшения
Катя, Володя и Лена делали к празднику украшения: гирлянды, звездочки и флажки. Катя не делала звездочки, а Лена не делала звездочки и гирлянды. Все вырезали украшения из бумаги разного цвета: желтого, красного и оранжевого. Флажки были красного цвета. Катя вырезала из оранжевой бумаги. Какие украшения и какого цвета делали Катя, Володя, Лена?
Решение
1. Катя не делала звездочки, Лена не делала звездочки и гирлянды (по условию). Флажки были красного цвета (по условию). Катя вырезала из оранжевой бумаги (по условию). Отметим эти факты на схеме линиями соответствующих типов.
гирлянды- желтые
звездочки-оранжевые
флажкикрасные
2. Из схемы видно, что Лена делала флажки. Значит, Катя делала гирлянды, тогда Володя делал звездочки. Отметим эти выводы на схеме.
- желтые
оранжевые
красные
З. Из схемы видно, что Лена вырезала красные флажки, а Катя — оранжевые гирлянды. Значит, Володя вырезал звездочки из желтой бумаги. Отметим эти выводы на схеме.
желтые
оранжевые
КРаСНые
 |
звездочки.
Задача 70. Модели
Юра, Коля, Саша и Дима делали модели. Двое делали модели из дерева, а двое — из картона. Коля и Дима делали модели из разного материала. Юра делал модель не из картона. Дима делал модель из картона. Получились три модели самолетов и одна модель корабля. Коля не делал модель самолета. Какую модель и из какого материала делал каждый из мальчиков?
Ответ: Коля делал корабль из дерева; Юра — самолет из дерева; Саша и Дима делали самолеты из картона.
Задача 71. Авиасалоны
В 1995 году состоялись три авиасалона в городах Файрфорд, Ле-Бурже и Москва, в которых участвовало по одному истребителю. В авиасалонах принимали участие истребители Грилпен, Фантом и Миг, которые выполняли фигуры пилотажа «колокол», «петля» и
«бочка» •
Известно, что:
1)Грилпен и Фантом не могут выполнять «колокол» ;
2)первые буквы в названиях двух самолетов и городов, где проводились авиасалоны, совпадают;
З) на авиасалоне в Файрфорде не выполнялась «бочка». Определите, на каком авиасалоне какой самолет выполнял какую фигуру пилотажа.
Решение
1. Самолеты Грилпен и Фантом не могут выполнять фигуру пилотажа «колокол» (по условию 1), значит, ее выполнял Миг. Отметим этот вывод на схеме.
Грилпен- - «
колокол»
Фантом- «петля»
Миг«бочка»
2.
 |
в Файрфорде.
Отсюда следует, что в Ле-Бурже выполнял полеты Грилпен. Отметим эти выводы на
схеме.
Грилпен«колокол»
Фантом«петля»
Миг«бочка»
З. На авиасалоне в Файрфорде не выполнялась «бочка» (по условию З), а в Москве выполнялся «колокол» (как видно из схемы), значит, в Файрфорде выполнялась «петля», а в Ле-Бурже — «бочка». Отметим эти выводы на схеме.
Грилпен-
«колокол»
Фантом«петля»
Миг«бочка»
Ответ: в Файрфорде Фантом показывал
фигуру пилотажа «петля», в Ле-Бурже Грилпен 
«бочку», в Москве Миг
— « колокол» •
Задача 72. Дома
Три девочки — Алиса, Вера и Катя — живут в разных домах. Кто-то из них живет в трехэтажном доме, а кто-то — в одноэтажном. Два дома имеют квадратные окна, один — прямоугольные. Трехэтажные и одноэтажные дома имеют окна разной формы. Алиса живет не в одноэтажном доме. Вера и Катя живут в разных домах. Катя живет в одноэтажном доме с квадратными окнами. Какие окна в доме Веры и сколько этажей в этом доме?
Ответ: Вера живет в трехэтажном доме с прямоугольными окнами.
Задача 73. Горные лыжи
 |
Ответ: у Оли лыжи и ботинки фирмы Тап,
у Лены лыжи фирмы Fisher, а ботинки — Dynastar, у Иры лыжи Dynastar, а ботинки 
Fisher.
Задача 74. Клоуны
Три клоуна — Бим, Бам и Бом — вышли на арену в красной, зеленой и синей рубашках. Их туфли были тех же трех цветов. У Бима цвета рубашки и туфель совпадают. У Бома ни туфли, ни рубашка не красные. Бам в зеленых туфлях, но в рубашке другого цвета. Как одеты клоуны?
Ответ: Бим в туфлях и рубашке красного цвета, Бом в синих туфлях и зеленой рубашке, Бам в зеленых туфлях и синей рубашке.
Задача 75. Музыканты
На концерте в
Санкт-Петербурге встретились трое мальчиков — Андрей, Юра и Денис, которые
играли на фортепиано, скрипке и виолончели. Они живут: один 
в
Санкт-Петербурге, другой в Москве, третий 
в Калининграде. Кто
где живет и на чем играет, если известно, что Юра не умеет играть на струнных
инструментах; у Дениса самый любимый инструмент — скрипка, и он на ней играет;
Юра любит гулять каждое воскресенье по Арбату, а Денис хочет побывать в
Эрмитаже, так как в его городе такого музея нет?
Ответ: Андрей живет в Санкт-Петербурге и играет на виолончели, Юра живет в Москве и играет на фортепиано, Денис живет в Калининграде и играет на скрипке.
Задача 76. Из Москвы в Санкт-Петербург
 |
Известно что:
1) все перечисленные лица живут в Москве, СанктПетербурге и Бологом;
2) все три пассажира живут в разных городах по
Октябрьской железной дороге;
З) все члены поездной бригады живут в одном городе;
4) пассажир Иванов живет в Москве;
5) кондуктор живет в городе Бологое;
6) пассажир однофамилец кондуктора живет в Санкт-Петербурге;
7) пассажир Петров не проживает там же, где его однофамилец;
8) Сидоров из поездной бригады выиграл у кочегара партию в бильярд.
Каковы фамилии членов поездной бригады и где живут они и пассажиры?
Решение
1. Все члены поездной бригады живут в Бологом (по условиям З, 5). Пассажир Иванов живет в Москве (по условию 4). Из условия 7 и из того, что все члены поездной бригады живут в Бологом, следует, что Петров не живет в Бологом. Из условия 8 следует, что Сидоров — не кочегар. Отметим выводы на схеме.
пассажиры: однофамильцы:
МоскваСидоров- - - - - - - кочегар
Бологое-с Иванов кондуктор
Санкт-Петербург-Петров машинист
2.
 |
пассажиры: однофамильцы:
МоскваСидоров
- - кочегар
БологоеИвановкондуктор
Санкт-ПетербургПетров- машинист
З. Из схемы видно, что кочегар — Иванов. Следовательно, Сидоров — машинист. Отметим выводы на схеме.
пассажиры: однофамильцы :
МоскваСидоров-
- кочегар
БологоеИвановкондуктор
Санкт-ПетербургПетров машинист
Ответ: пассажиры проживают: Сидоров — в Бологом, Иванов — в Москве, Петров — в СанктПетербурге; поездная бригада проживает в городе Бологое, причем Сидоров — машинист, Иванов — кочегар, Петров — кондуктор.
Задача 77. На выставке камней-самоцветов
В Санкт-Петербурге была открыта выставка самоцветов. Маша побывала на ней и узнала, что у каждого месяца есть свой камень-талисман и он что-то обозначает. Ее заинтересовали три месяца: июнь, июль, сентябрь. Их камни рубин, сапфир, жемчуг. Значение этих камней: мудрость, здоровье, благополучие.
Узнайте, у какого месяца какой камень-талисман и что он обозначает, если известно, что:
1) жемчуг и рубин не принадлежат сентябрю;
2) июнь и июль ничего не говорят нам о мудрости; З) здоровье не соответствует рубину;
 |
Решение
1. Отметим на схеме пунктирными линиями те несоответствия, которые известны из условия задачи.
Рубинздоровье
сапфирблагополучие
жемчуг- •
мудрость
2. Отсюда сразу видно, что сентябрю соответствуют сапфир и мудрость, июню — здоровье. Отметим эти соответствия сплошными линиями.
РУбињЗДОРОВЬе сапфирблагополучие
жемчуг-мудрость
З. Июню соответствует жемчуг, так как здоровье не соответствует рубину (по условию З), а для июня характерно здоровье (по доказательству). Сапфир же — камень сентября (по доказательству). Следовательно, камень июля — рубин. Из схемы также видно, что июлю соответствует благополучие. Тогда камень июня — жемчуг. Отметим выводы на схеме.
Рубин
сапфир
жемчуг
Ответ: июнь жемчуг здоровье; июль 
бин
— благополучие; сентябрь — сапфир 
мудрость.
Задача 78. В поезде
 |
журналист, дизайнер и
зубной техник. Они читали газеты: «Правда», «Жизнь России» и «Аргументы и
факты» .
Известно что:
1) Галя не доктор;
2) Аня никогда не читала «Аргументы и факты»;
З) у имени, профессии и названия газеты одного из пассажиров совпадают первые буквы.
Кто что читал и у кого какая профессия?
Решение
1. Из условия З следует, что Женя — журналист и читала газету «Жизнь России» (только для буквы Ж можно найти такое тройное совпадение). Галя не доктор (по условию 1). Аня не читала «Аргументы и факты» (по условию 2). Отметим выводы на схеме.
журналист-
-Аняч, «Правда» докторх -Таля- «Жизнь России» зубной техник- - ЖеняЕ
«Аргументы и факты»
2. 
Из схемы видно, что
Аня читала «Правду». Следовательно, Галя читала «Аргументы и факты». Галя не
доктор (по условию 1) и не журналист (по доказательству), значит, она — зубной
техник, а Аня 
доктор. Отметим выводы на схеме. журналист Анях——,
«Правда»
доктор«Жизнь России»
зубной техник«Аргументы и факты»
Ответ: Женя читала «Жизнь России», по профессии она журналист; Аня читала «Правду», по профессии она доктор; Галя читала «Аргументы и факты» , по профессии она зубной техник.
Задача 79. Спортсмены
 |
Известно, что:
1) Джессика не любит хоккей, но хотела бы позаниматься с друзьями своим любимым видом спорта или просто съездить и посмотреть Монреаль и Денвер;
2) Ник хотел бы поехать в Денвер;
З) Линда плохо катается на коньках.
Кто в каком городе живет и каким видом спорта занимается?
Решение
1. Из
условия 1 следует, что Джессика не играет в хоккей и не живет в Денвере и
Монреале. Из условия 2 следует, что Ник живет не в Денвере. Из условия З
следует, что Линда занимается не фигурным катанием и не хоккеем. Отметим выводы
на схеме. фигурное катаниеч
Джессика»
Лас-Вегас
|
хоккеи•: |
|
|
горные лыжи |
- Денвер |
2. Из схемы видно, что в Денвере живет Линда и она занимается горнолыжным спортом, Джессика живет в Лас-Вегасе, а Ник занимается хоккеем. Отметим выводы на схеме.
фигурное катанињ ДЭкеСсика=—Лас-Вегас
хоккей*Монреаль горные лыжиДенвер
З. Отсюда видно, что Ник живет в Монреале, а Джессика занимается фигурным катанием. Отметим выводы на схеме.
фигурное
катаниек—--Джессика
хоккей
горные лыжи Денвер
 |
Задача 80. Сыновья военнослужащих
Гриша, Миша и Игорь — сыновья военнослужащих. У одного из них отец — офицер флота, у второго — ракетчик, а у третьего — десантник. Юноши приняли решение тоже стать военными. Один из них попал на флот, другой стал ракетчиком, а третий десантником. Михаил по состоянию здоровья не попал в десантники, а Игорь не попал на флот. Не попал на флот и сын моряка. Гриша, как и отец, стал ракетчиком. Кто кем стал и кем служат их отцы?
Решение
1. По условию: Миша не десантник, Игорь не моряк, Гриша — ракетчик, отец Гриши тоже ракетчик. Отметим данные факты на схеме.
отцы: сыновья:
моряк -Гриша, моряк
ракетчик - -Миш&ракетчик
десантникИгорь— десантник
2. Из схемы видно, что Игорь — десантник, а Миша — моряк. Миша не сын моряка, так как сын моряка не моряк (по условию), значит, Миша — сын десантника. Тогда Игорь — сын моряка. Отметим выводы на схеме.
отцы: сыновья:
морякморяк
ракетчикракетчик
десантникдесантник
 |
Задача 81. Дерево-покровитель
По гороскопу древних друидов (вещих мудрецов Галлии) у каждого человека есть дерево-покровитель, которое дает некоторую черту характера этого человека. Например: у человека, родившегося в мае, дерево-покровитель каштан, значит, этот человек изобретательный.
Даны три месяца, три качества и три дерева: январь, декабрь, август; отвага, доброжелательность, красота; сосна, кипарис, тополь. Узнайте, что к чему относится, если известно, что:
1) к январю не относится ни доброжелательность, ни отвага, ни сосна, ни тополь;
2) тополь не является покровителем августа;
З) сосна, кипарис и отвага не соответствуют одно другому по гороскопу друидов.
Решение
1. Январю не соответствует ни доброжелательность, ни отвага, ни сосна, ни тополь (по условию 1). Тополь не соответствует августу (по условию 2). Отваге не соответствует ни сосна, ни кипарис (по условшо З). Отметим данные факты на схеме.
январь—:--_-- ------сосна :
— отвага
декабрь- доброжелательность
август- • тополь красота
2. Из схемы видно, что январю соответствует красота, тополю — декабрь, а отваге — тополь. Отметим выводы на схеме.
январь -- отвага
 |
август-красота
З. Теперь видно, что сосне соответствует август и доброжелательность, следовательно, кипарису соответствует красота и январь. Отметим выводы на схеме.
январь - отвага
декабрьдоброжелательность
августкрасота
Ответ: январь — кипарис — красота, август — сосна доброжелательность, декабрь тополь — отвага.
Задача 82. Три учительницы
Три учительницы — Ирина Васильевна, Дарья Михайловна и Софья Петровна преподают различные предметы — химию, биологию и физику в школах Минска, Львова и Курска.
Известно, что:
1) Ирина Васильевна работает не в Минске, а Дарья Михайловна — не во Львове;
2) учительница, живущая в Минске, преподает не физику;
З) учительница, работающая во Львове, преподает химию;
4) Дарья Михайловна преподает не биологию.
Какой предмет и в каком городе преподает каждая учительница?
Решение
1.
 |
физика-Минск
химия'Львов
биология- - - -- - -Дарья Михайловна Курск
2. Дарья Михайловна живет не во Львове (по условию 1), значит, она не преподает химию. Дарья Михайловна не преподает также и биологию (по условию 4). Следовательно, она преподает физику. Но учительница из Минска не преподает физику (по условию 2), значит, Дарья Михайловна живет не в Минске, а в Курске. Следовательно, Ирина Васильевна живет не в Курске, но также она не из Минска (по условию 1), значит, Ирина Васильевна из Львова. Следовательно, Софья Петровна из Минска. Отметим выводы на схеме.
З. Так как учительница из Львова
преподает химию (по условию З), а во Львове живет Ирина Васильевна (по
доказательству), Ирина Васильевна — учительница химии. Следовательно, Софья
Петровна 
учительница биологии. Отметим выводы на
схеме.
физика-
химия
биология
Ответ: Ирина Васильевна живет во Львове и преподает химию, Дарья Михайловна живет в Курске и преподает физику, Софья Петровна живет в Минске и преподает биологию.
Задача 83. Профессии
Антонов, Малеев и Марков живут в разных городах и имеют разные профессии. Один живет в Москве, другой — в Минске, третий — в Астрахани. Один работает механиком, другой — агрономом, третий — артистом.
Определите местожительство и профессию каждого, если известно, что:
1) Марков бывает в Москве лишь во время отпуска, хотя все его родственники живут в Москве; 2) жена артиста приходится Маркову сестрой;
З) у двух из этих людей название профессий и городов, в которых они живут, начинаются с той же буквы, что и их фамилии.
Решение
1. Из условия 1 следует, что Марков не москвич. Сестра Маркова приходится женой артисту (по условию 2), она — родственница Маркова, значит, живет в Москве. Следовательно, москвич артист. Из условия 2 также следует, что Марков не артист. Отметим данные факты на схеме.
Москвамеханик
Минскагроном
Астраханьартист
2.
 |
Астрахань, Антонов). Механик не живет в
Москве и Астрахани (по доказательству), значит, он живет в Минске. Марков не
артист и не агроном (по доказательству), значит, он механик. Следовательно,
Малеев — артист и живет в Москве. Отметим выводы на схеме.
Москвамеханик
Минскагроном
Астраханьартист
Ответ: Марков — механик и живет в Минске, Антонов — агроном и живет в Астрахани, Малеев — артист и живет в Москве.
Задача 84. Цветы знаков зодиака
Ученые, долгое время наблюдавшие за людьми, ро-
дившимися в разные месяцы года, заметили, что их черты характера различаются. Они составили зодиакальный гороскоп, в котором каждому месяцу поставили в соответствие созвездие (знак зодиака). А флористы
(исследователи цветов) каждому знаку зодиака предписали цветок, который обладает чертами человека, родившегося в этом месяце.
Выберем три знака зодиака: Водолей, Рыбы и Овен.
Им соответствуют цветы: омела, мимоза и гортензия. Эти цветы обладают определенными свойствами: щедростью, чувственностью и любопытством.
Узнайте, какому знаку зодиака какой цветок принадлежит и каким свойством он обладает, если известно, что:
1) цветок знака Рыб не омела, но свойство цветка рыб — чувственность;
2) свойство гортензии — не любопытство, она не принадлежит к знакам Водолея и Рыбы.
Решение
1. Отметим на схеме условия задачи.
любопытство омела- Водолей
 |
щедрость гортензия- Овен
2. Из схемы видно, что цветок гортензия соответствует знаку Овна. Цветок знака Рыб — не омела (по условию 1) и не гортензия (по условию 2), значит, цветок знака Рыб мимоза. Следовательно, цветок омела соответствует знаку Водолея. Отметим выводы на схеме.
любопытствоВодолей
чувственностьРыбы
щедрость гортензия Овен
З. Из схемы видно, что свойство знака Рыб — чувственность, значит, мимоза обладает данным свойством. Цветок гортензии не обладает любопытством (по условию 2) и не обладает чувственностью (по доказательству), значит, свойство гортензии — щедрость. Следовательно, любопытство — свойство омелы.
Ответ: цветок Водолея — омела, его свойство — любопытство; цветок Рыб — мимоза, его свойство чувственность; цветок Овна гортензия, его свойство — щедрость.
Задача 85. Строительство
В небольшом садоводческом товариществе на берегу озера рядом стоят три дачных домика: кирпичный, брусовый и шлаковый с железной, шиферной и рубероидной крышами. В них живут семьи Андреевых, Васильевых и Рощиных. Васильевы живут в брусовом доме, а крыша их дома не покрыта рубероидом. Андреевы помогали соседям покрывать кирпичный дом рубероидом. Васильевы часто ходят купаться на озеро и навещают друзей, которые живут в доме с железной крышей.
Какая семья в каком доме с какой крышей живет?
Ответ: семья Андреевых живет в
шлаковом доме с железной крышей, семья Васильевых 
в брусовом доме с
шиферной крышей, семья Рощиных — в кирпичном доме с рубероидной крышей.
Задача 86. Дочери писательницы
Три дочери писательницы Дорис Кей — Джуди, Айрис и Линда — тоже очень талантливы. Они приобрели известность в разных видах искусств: пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго.
Известно, что:
1) Джуди живет не в Париже, а Линда — не в Риме;
2) парижанка не снимается в кино; З) та, кто живет в Риме, певица; 4) Линда равнодушна к балету.
Где живет Айрис и какова ее профессия?
Решение
1. Отражаем в таблице нулями и единицами условия 1
|
|
Город |
|
Имя |
Вид искусства |
||
|
Париж |
Рим |
Чикаго |
Пение |
Балет |
Кино |
|
|
|
|
|
Джуди |
|
|
|
|
|
|
|
Айрис |
|
|
|
|
|
|
|
Линда |
|
О |
|
2.
 |
|
|
Город |
|
Имя |
Вид искусства |
||
|
Париж |
Рим |
Чикаго |
Пение Балет |
Кино |
||
|
|
|
|
Джуди |
|
|
|
|
|
|
|
Айрис |
|
|
|
|
|
|
|
Линда |
|
|
|
З. Из таблицы сразу видно, что Линда — киноактриса, следовательно, Джуди и Айрис не снимаются в кино. Заполняем соответствующие ячейки столбца «Кино».
|
|
Город |
|
Имя |
Вид искусства |
||
|
Париж |
Рим |
Чикаго |
Пение |
Балет |
Кино |
|
|
|
|
|
Джуди |
|
|
|
|
|
|
|
Айрис |
|
|
|
|
|
|
|
Линда |
О |
|
1 |
4. Парижанка не снимается в кино (по условию 2), следовательно, Линда живет не в Париже. Но она экивет и не в Риме. Следовательно, Линда живет в Чикаго. Заполняем соответствующие ячейки строки «Линда» и столбца «Чикаго». Так как Линда и Джуди живут не в Париже, там живет Айрис. Значит, Джуди живет в Риме. Заполняем левую часть табли-
цы. Так как Джуди живет в Риме, она является певицей (это следует из условия З). А так как Линда — киноактриса, Айрис — балерина. Заполняем правую часть таблицы. Окончательно имеем:
|
|
Город |
|
Имя |
Вид искусства |
||
|
Париж |
Рим |
Чикаго |
Пение |
Балет |
Кино |
|
|
|
1 |
О |
Джуди |
1 |
|
|
|
1 |
|
о |
Айрис |
|
1 |
|
|
|
|
1 |
Линда |
|
О |
1 |
Ответ: Айрис — балерина. Она живет в Париже.
Задача 87. Встреча с одноклассниками
 |
бег, страсть третьего
— регби. Юра сказал, что на туризм ему не хватает времени, хотя его сестра —
единственный врач в семье — заядлый турист. Врач сказал, что он разделяет
увлечение коллеги. Забавно, что у двоих из друзей в названиях их профессий и
увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Решение
1. Здесь исходные данные разбиваются на тройки « имя профессия увлечение». Из слов Юры ясно, что он не увлекается туризмом и он — не врач. Из слов врача следует, что он турист.
2. Буква «а», присутствующая в слове «врач», указывает на то, что Влад — тоже не врач. Если бы Влад был врачом, то либо Тимур, либо Юра был бы юристом. Получилось бы, что сразу два друга имели бы в названиях профессий буквы из их имен. Следовательно, врач — Тимур.
|
Имя |
Профессия |
Увлечение |
|
Юра |
|
|
|
Тимур |
Врач |
Туризм |
|
Влад |
|
|
З. В имени Тимур есть буквы «т» и «р», встречающиеся в слове «туризм». Следовательно, два друга, в названиях профессий и увлечений которых не встречается ни одна буква их имен, — это Юра и Влад. Тогда Юра — не юрист и не регбист, так как в его имени содержатся буквы «ю» и «р». Тогда окончательно мы получим:
|
Имя |
Профессия |
Увлечение |
|
юра |
Физик |
Бег |
|
Тимур |
Врач |
Туризм |
|
Влад |
Юрист |
Регби |
 |
Задача 88. Вчера вечером
Вчера вечером:
1)Андрей отправился на концерт;
2)Борис провел все время с Ольгой; З) Евгений так и не увиделся с Розой;
4) Полина побывала в кино;
5) Роза посмотрела спектакль в театре;
6) какая-то пара посетила художественную выставку.
Кроме тех, кого мы уже назвали, постоянно членами той же компании были Дмитрий и Серафима. Вместе с каждым юношей была девушка. Все пары были в разных местах.
Кто с кем был и где?
Решение
1. По условиям 1, 4 и 5 имеем:
|
Имя |
Место досуга |
|
||
|
Концерт |
Кино |
Театр |
Худ. выставка |
|
|
Андрей |
1 |
|
|
|
|
Борис |
|
|
|
|
|
Евгений |
|
|
|
|
|
митрий |
|
|
|
|
|
Ольга |
|
|
о |
|
|
Роза |
|
|
1 |
|
|
Полина |
|
1 |
о |
|
|
Серафима |
|
|
|
|
2.
 |
|
Имя |
|
Место досуга |
|
||
|
Концерт |
Кино |
Театр |
Худ. выставка |
||
|
Андрей |
1 |
|
|
|
|
|
Борис
Евгений |
|
|
|
|
|
|
|
|
|
|
||
|
Дмитрий |
|
1 |
|||
|
Ольга Роза |
|
О |
О 1 |
О
|
|
|
Полина
Серафима |
|
1 |
|
||
|
|
|
|
|||
З. Полина была в кино и не с Андреем (это следует из условия 1), не с Борисом (это следует из условия 2), не с Дмитрием (он был с Розой по доказательству), значит, она была там с Евгением. Ставим в ячейку «Евгений, Кино», цифру 1, а в остальные ячейки столбца «Кино» и строки «Евгений» нули.
|
Имя |
Место досуга |
|||
|
Концерт |
Кино |
Театр |
Худ. выставка |
|
|
Андрей |
1 |
|
|
|
|
Борис |
|
|
о |
|
|
Евгений |
|
1 |
|
|
|
Дмитрий |
|
|
1 |
|
|
Ольга |
|
|
|
|
|
Роза |
|
|
1 |
|
|
Полина |
|
1 |
о |
|
|
Серафима |
|
|
|
|
 |
|
Имя |
|
Место досуга |
|
|
|
Концерт |
Кино |
Театр |
Худ. выставка |
|
|
Андрей |
1 |
|
|
|
|
Борис |
|
|
|
1 |
|
Евгений |
О |
1 |
|
|
|
Дмитрий |
|
|
1 |
1 |
|
Ольга |
|
|
|
|
|
Роза |
|
|
1 |
|
|
Полина |
|
1 |
|
|
|
Серафима |
1 |
|
|
|
Ответ: Андрей с Серафимой были на концерте, Евгений с Полиной в кино, Дмитрий с Розой — в театре, Борис с Ольгой посетили художественную выставку.
Задача 89. Студенты
В одном из петербургских институтов на разных курсах учатся четыре друга. Самый младший из них учится на 1-м курсе, а самый старший — на 4-м.
Определите имя и фамилию каждого студента и курс, на котором он учится, если известно, что:
1)Борис персональный стипендиат по итогам предыдущего курса;
2)Василий должен летом ехать на практику в Омск, а Иванов собирается ехать домой в Донецк; З) Николай курсом старше Петра;
4) Борис и Орлов — коренные петербуржцы;
5) Крылов в прошлом году окончил школу и поступил на тот же факультет, где учился Зуев;
6) Борис иногда пользуется прошлогодним конспектом Василия.
Решение
1.
 |
|
Имя |
Фамилия |
Номер курса |
||||||
|
Зуев |
Иванов |
Крылов |
Орлов |
1 |
2 |
з |
|
|
|
Борис |
|
|
|
|
|
|
|
|
|
Василий |
|
|
|
|
|
|
|
|
|
Николай |
|
|
|
|
|
|
|
|
|
Петр |
|
|
|
|
|
|
|
|
2. Из таблицы видно, что на 1-м курсе учится Петр. Николай курсом старше Петра (по условию З), а Петр — на 1-м курсе (по доказательству). Значит, на 2-м курсе — Николай. Из условия 6 следует, что Борис на курс младше Василия, но оба они учатся не на 1-м и не на 2-м курсе (по доказательству). Значит, Борис — на 3-м курсе, а Василий — на 4-м курсе. Получаем таблицу:
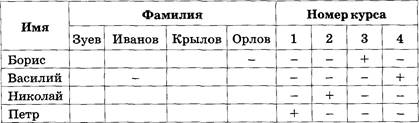
5-1703
З. Из условия 5 следует, что Крылов учится на 1-м курсе, значит, Крылов — Петр. Из условий 2 и 4 следует, что Иванов не Борис. Кроме того, Иванов не Петр (по доказательству), значит, Иванов — Николай. Из условия 4 следует, что Борис не Орлов, но он также не Крылов (это Петр) и не Иванов. Значит, Борис — Зуев, следовательно, Василий — Орлов. Окончательно получим:
|
Имя |
Фамилия |
Номер курса |
||||||
|
Зуев |
Иванов |
Крылов |
Орлов |
1 |
2 |
з |
4 |
|
|
Борис |
|
|
|
|
|
|
|
|
|
Василий |
|
|
|
|
|
|
|
|
|
Николай |
|
|
|
|
|
|
|
|
|
Петр |
|
|
|
|
|
|
|
|
 |
Задача 90. Незадачливый ПСИХОЛОГ
Один психолог решил заняться изучением того, как влияет на нервную систему человека поездка в переполненном трамвае в часы пик. Для этого он опросил по одному пассажиру с каждого из четырех маршрутов трамвая: N2N2 55, 15, 25 и 33. Среди опрошенных, которых звали Андрей, Петр, Виктор и Иван, оказались представители четырех профессий: слесарь, электромонтер, маляр и фрезеровщик. К сожалению, поездки в битком набитых трамваях основательно истрепали нервы самому психологу. Неудивительно, что он напрочь забыл, у кого из опрошенных какая профессия и кто на каком трамвае ездит. В памяти нашего психолога сохранились лишь бессвязные отрывки из того, что рассказал каждый из опрошенных о своем маршруте.
Вот что ему припомнилось:
1) номер трамвая, на котором ездит Виктор, начинается не с двойки;
2) о трамвае № 33 рассказывал кто-то из рабочих-металлистов;
З) номер трамвая, на котором ездит фрезеровщик, составлен из таких цифр, что их сумма равна количеству букв имени фрезеровщика;
4) Иван ездит на трамвае, номер которого состоит из двух одинаковых цифр;
5) имя электромонтера начинается с буквы «В»;
6) Андрей спросил психолога, где лучше сойти, чтобы пересесть на трамвай N2 25;
7) Иван сказал кому-то из пассажиров: «Вы сели не на тот трамвай, вам надо пересесть на № 55».
Определите имя и профессию каждого пассажира, а также номер трамвая, на котором он ездит.
Решение
1. Иван ездит на трамвае с номером из двух одинаковых цифр (по условию 4), но не на N2 55 (это следует из условия 7), значит, Иван ездит на трамвае № 33.
2.
 |
З. На трамвае № 33 ездит Иван (по доказательству), значит, на трамвае 15 ездит или Андрей, или Виктор. Но так как по условию 6 Андрей не может ехать на трамвае .N2 25, Андрей ездит именно на трамвае № 15 и он — фрезеровщик, поскольку из условия 5 следует, что Виктор — электромонтер.
4. Виктор ездит на трамвае, номер
которого начинается не с двойки (по условию 1), но не на трамвае № 15 и не на
трамвае 33 (по доказательству), значит, он ездит на трамвае № 55. Получаем, что
Петр 
маляр и он ездит на трамвае № 25.
Окончательно получим:
|
Имя |
Профессия |
Номер трамвая |
||||||
|
Слесарь |
Электро- маляр монтер |
Фрезеровщик |
55 |
15 |
25 |
33 |
||
|
Андрей |
|
|
|
|
|
|
|
|
|
Петр |
|
|
|
|
|
|
|
|
|
Виктор |
|
|
|
|
|
|
|
|
|
Иван |
|
|
|
|
|
|
|
|
Ответ: Андрей — фрезеровщик, ездит на
трамвае 
15; петр маляр, ездит на трамвае N2 25;
Виктор электромонтер, ездит на трамвае № 55; Иван слесарь, ездит на трамвае №
33.
Задача 91. Рыбалка
 |
одну рыбу, четвертый — ни одной. Известно,
что:
1) тот, кто поймал две рыбы, в качестве насадки пользовался не червями и не живцом;
2) тот, кто ловил на живца, поймал меньше рыб, чем Федор;
З) лучшей насадкой в тот день оказались мухи на них было поймано больше всего рыбы;
4) Толик пользовался в качестве насадки опарышами;
5) Сергей поймал больше, чем тот, кто ловил на живца, но не больше всех;
6) четвертого рыболова зовут Иван.
Кто из них сколько поймал и что использовал в качестве насадки?
Решение
1. Федор ловил не на живца и поймал хотя бы одну рыбу (это следует из условия 2). Лучшей насадкой в тот день были мухи (по условию З), значит, на мух поймали трех рыб. Следовательно, на опарышей были пойманы две рыбы (это следует из доказанного и из условия 1), и этим рыболовом был Толик (это следует из условия 4). Сергей поймал хотя бы одну рыбу, но не три рыбы (это следует из условия 5). Получаем таблицу:
|
|
Имя |
Наживка |
||||||
|
Федор |
Сергей |
Толик |
Иван |
Черви |
Опарыши |
Живец |
Мухи |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
2.
 |
Значит, он ловил на червей, а Иван — на живца. Окончательно получим:
|
|
Имя |
Наживка |
||||||
|
Федор |
Сергей |
Толик |
Иван |
Черви |
Опарыши |
Живец |
Мухи |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
З |
|
|
|
|
|
|
|
|
Ответ: Сергей ловил на червей, поймал одну рыбу; Федор ловил на мух, поймал три рыбы; Толик ловил на опарышей, поймал две рыбы; Иван ловил на живца, ничего не поймал.
Задача 92. Увлечения
Витя, Саша, Андрей и
Толя собирали модели самолетов. Двое делали модели из белой пластмассы, а двое 
из
серой. Саша и Андрей, Саша и Толя делали модели из пластмассы разного цвета.
Получились три модели самолетов фирмы «Ту» и одна — фирмы «Су». Какую модель из
какого материала делал каждый из мальчиков, если Саша делал модель самолета
фирмы «Су» из белой пластмассы?
Ответ: Саша делал самолет фирмы «Су» из белой пластмассы; Андрей и Толя — фирмы «Ту» из серой пластмассы; Витя — фирмы «Ту» из белой пластмассы.
Задача 93. Обновление дачного домика
 |
Сколько было каждой краски и где она находилась?
Ответ: 5 литров белой краски находились в ведре, З литра синей краски в круглой банке, 2 литра желтой краски — в плоской банке, 4 литра черной краски — в бутыли.
Задача 94. В купе поезда
В купе одного из вагонов поезда «Москва—Одесса» ехали москвич, петербуржец, туляк, киевлянин, харьковчанин и одессит. Их фамилии начинались с букв «А» , «Б», «В», «Г», «Д» и «Е». В дороге выяснилось, что:
1) А. и москвич — врачи;
2) Д. и петербуржец — учителя;
З) В. и туляк — инженеры;
4) Б. и Е. — участники Великой Отечественной войны, а туляк в армии совсем не служил;
5) харьковчанин старше А.;
6) одессит старше В.;
7) Б. и москвич сошли в Киеве;
8) В. и харьковчанин сошли в Виннице.
Определите профессию и место жительства каждого из пассажиров.
Решение
1.
 |
2.
Из таблицы видно, что А. — врач, а Д. — учитель. Туляк — инженер
(по условию З), значит, А. и Д. не туляки. Следовательно, туляк — Г., и он
инженер. в. — инженер (по условию З), значит, он не жи
тель Москвы,
Санкт-Петербурга (это следует из условий 1 и 2). Следовательно, В. — житель
Киева. А. не петербуржец (это следует из условий 1 и 2), не туляк, не киевлянин
(по доказательству), значит, А. — одессит. Б. не харьковчанин (это следует из
условий 7 и 8) и не житель Тулы, Киева и Одессы (по доказательству), значит, Б.
— житель СанктПетербурга; следовательно, Б. — учитель. Москвич врач, а Д. —
учитель (по условиям 1 и 2) и А., Б.,
— не москвичи (по
доказательству), значит, москвич — Е., а харьковчанин — Д. Отсюда: Е. 
врач
(это следует из условия 1 и из доказанного). Окончательно получим:
|
Буква |
Город |
|
Профессия |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: А. — одессит, врач; Б. —
петербуржец, учитель; В. — киевлянин, инженер; Г. — туляк, инженер; Д. —
харьковчанин, учитель; Е. 
москвич, врач.
Рассмотрим теперь
несколько задач, в которых не три набора элементов, между которыми требуется
установить соответствие, а четыре. При решении таких задач с помощью таблиц
рекомендуется к основной таблице добавлять дополнительные секции для большей
понятности и наглядности. При этом ответ часто получается при не до конца
заполненной расширенной таблице. Плюсы и минусы в ячейки расставляются
аналогично тому, как это делалось в задачах с тремя элементами.
Задача 95. Школьники
Три друга — Алеша, Боря и Володя — учатся в разных школах Новгорода — ТФ 1, № 8, № 30. Все они экивут на разных улицах — Рогатица, Газон и Ломоносова. Причем один из них любит математику, второй — биологию, а третий — химию.
Известно, что: 1) Алеша не живет на ул. Рогатица, а Боря не живет на ул. Газон;
2) мальчик, живущий на ул. Рогатица, не учится в школе № 30;
З) мальчик, живущий на ул. Газон, учится в школе
1 и любит математику;
4) Володя учится в школе № 30;
5) ученик школы № 8 не любит химию. В какой школе учится каждый из друзей, на какой улице он живет и какой предмет любит?
Решение
 |
1. Алеша не живет на улице Рогатица, а Боря не живет на улице Газон (по условию 1). Соединим пунктирной линией элементы множеств: «Алеша» и «ул. Рогатица»; «Боря» и «ул. Газон».
2. Мальчик, живущий на ул. Рогатица, не учится в школе .N2 30 (по условию 2). Соединим пунктирной линией «ул. Рогатица» и «школа № 30».
З. Мальчик, живущий на ул. Газон,
учится в школе 
1 и любит математику (по условию З).
Соединим сплошными линиями: «школа № 1» и «математика»; «школа № 1» и «ул.
Газон»; «ул. Газон» и «математика».
4. Володя учится в школе 30 (по условию 4). Соединим сплошной линией«Володя» и «школа 30».
5. Ученик школы № 8 не любит химию. Соединим пунктирной линией «школа 8» и «химия».
6. Теперь из схемы видно, что ученик школы № 8 любит биологию, а ученик школы 30 любит химию.
Соответствующие элементы множеств соединим сплошными линиями.
7. Из схемы видно, что ученик школы № 30 не живет на ул. Рогатица и ул. Газон, следовательно, он экивет на ул. Ломоносова, но тогда ученик школы № 8 живет на ул. Рогатица. Соответствующие элементы соединим сплошными линиями.
8. При этом, очевидно, следует соединить сплошными линиями элементы: «ул. Рогатица» и «биология»; «химия» и «ул. Ломоносова».
9. Анализируя
схему, увидим, что Володя живет на улице Ломоносова, Алеша 
на улице
Газон, Боря — на улице Рогатица. Окончательно получим:
ул.
Газон ул. Рогатица ул. Ломоносова
 |
Ответ: Алеша живет на улице Газон, учится в школе № 1 и любит математику; Боря живет на улице Рогатица, учится в школе № 8 и любит биологию; Володя живет на улице Ломоносова, учится в школе N2 30 и любит химию.
Задача 96. Отъезд на работу
У подъезда паркуются четыре машины: «Жигули», «Волга», «Москвич» и «Запорожец». Они красного, желтого, белого и зеленого цветов. По утрам на них уезжают художник, пекарь, учитель и инженер. Происходит это в 8, 9, 10 и 12 часов.
Определите, кому какая машина принадлежит, какого она цвета и когда отъезжает, если известно, что:
1) у учителя не «Москвич»;
2) «Запорожец» не белый, а «Волга» не желтая;
З) инженер уезжает сразу после «Запорожца» ;
4) пекарь на своей желтой машине уезжает не в 9 и не в 12;
5) раньше всех уезжает учитель;
6) художник уезжаёт позже красного «Москвича».
« Жигули »
« Волга»
«Москвич» «Запорожец»
Желтый
Белый
Красный
 |
8 часов
9 часов
10 часов
12 часов
Ответ: у пекаря желтые «Жигули», он уезжает в 10 часов; у художника белая «Волга», он уезжает в 12 часов; у инженера красный «Москвич», он уезжает в 9 часов; у учителя зеленый «Запорожец», он уезжает в 8 часов.
Задача 97. Факультеты
Студенты Васильев, Алексеев, Дмитриева и Сергеев обучаются на физическом, математическом, филологическом и искусствоведческом факультетах в четырехэтажном здании университета. Согласно расписанию, им нужно посетить занятия по истории, литературе, иностранному языку и черчению. Все эти занятия проводятся в аудиториях, расположенных на разных этажах.
Известно, что:
1) занятия по иностранному языку проводятся этажом выше занятий по истории, а занятия по литературе — этажом выше занятий по черчению;
2) студентка Дмитриева не занимается ни литературой, ни иностранным языком;
З) на физическом факультете изучают черчение;
4) студент Сергеев занимается на 1-м этаже;
5) на 3-м этаже работает искусствоведческий факультет;
6) Дмитриева обучается на более высоком этаже, чем Алексеев, но более низком, чем Васильев;
7) Васильев не учится на математическом факультете.
 |
Физический
Математический
Филологический
Искусствоведческий
1 2 з
4
История
Литература
Иностранный язык +
Черчение
Ответ: Васильев: филологический, 4-й этаж, иностранный язык; Алексеев: математический, 2-й этаж, литература; Дмитриева: искусствоведческий, 3-й этаж, история; Сергеев: физический, 1-й этаж, черчение.
Задача 98. Спортивный лагерь
В летний спортивный
лагерь приехали Женя, Юра, Митя и Вася. Один из них занимается боксом, другой 
хоккеем,
третий — футболом, четвертый — бейсболом: один — 1 год, другой — З года, третий
— 5 лет, четвертый — 6 лет. В лагере они провели 4, 6, 8 и 12 недель.
Определите, кто каким видом спорта и сколько лет занимается и какое время
каждый провел в лагере, если известно, что:
1)тот, кто пробыл в лагере меньше всех, — футболист;
2)Митя занимается спортом З года, а Юра не хоккеист;
З) Вася в спорте на 2 года дольше, чем Митя;
4) футболист занимается спортом на 5 лет дольше, чем боксер;
5) хоккеист пробыл в лагере дольше, чем Митя, но меньше, чем Женя.
 |
6 недель
8 недель
12 недель
1 год
З года 5 лет 6 лет
Бокс
Футбол
Бейсбол
Хоккей
Ответ:
Вася: хоккей, 8 недель, 5 лет; Юра: футбол, 4 недели, 6 лет; Митя: бейсбол, 6 недель, З года; Женя: бокс, 12 недель, 1 год.
Завершая раздел,
приведем несколько задач, которые представляют ббльшую трудность, чем описанные
выше, из-за более сложных условий и менее явно прослеживаемых взаимосвязей
между элементами. Схемы их решения отличаются от предложенных выше.
Задача 99. Воскресник
|
28 штук.
У кого какие имя и фамилия?
Решение
1. Все части были по 0,5 метра, значит, из двухметровых кругляков можно было напилить по 4 части из каждого. Следовательно, у Володи с Мишей количество напиленных частей должно быть кратно 4. Кратно 4 только количество частей, напиленных Медведевым и Евдокимовым, — 28. Следовательно, Медведев — фамилия Володи, Евдокимов — фамилия Миши.
2. Так как из полутораметровых кругляков можно напилить по З части полуметровой длины, значит, у Пети с Костей количество напиленных отрезков должно быть кратно З. Кратно З число 27 — количество отрезков, напиленных Галкиным и Пастуховым. Значит, Галкин — Петя, а Пастухов — Костя.
14 з
З. Остается только одна бригада: Вася Лавров, Федя Котов. Проверим: Вася и Федя могли напилить только четное количество частей, а число 26 — четное. Окончательно получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Володя |
|
|
|
|
|
|
|
|
Миша |
|
|
|
|
|
|
|
|
Петя |
1,5 м |
|
|
|
|
|
|
|
Костя |
1,5 м |
|
|
|
|
|
|
|
Вася |
|
|
|
|
|
|
|
|
Федя |
|
|
|
|
|
|
|
|
Кол-во отрезков |
|
26 |
26 |
27 |
27 |
28 |
28 |
Ответ: Володя Медведев, Миша Евдокимов, Петя Галкин, Костя Пастухов, Вася Лавров, Федя Котов.
Задача 100. Дружеский ужин
Три молодые супружеские пары собрались как-то раз на дружеский ужин. Завязалась беседа. Настроение у всех было превосходное, дамы — явно молоды, поэтому вопросы о возрасте присутствующие не исключали.
Были высказаны следующие утверждения:
1) Андрей: «Каждый из трех мужей на 5 лет старше своей жены»;
2) Ева: «Не стану скрывать — я самая старшая из всех жен»;
З) Игорь: «Нам с Юлией вместе 52 года»;
4) Леонид: «Всем нам шестерым вместе 151 год»; 5) Юлия: «Нам с Леонидом вместе 48 лет» .
К сожалению, Марта так и не смогла принять участие в застольной беседе, поскольку ей пришлось выполнять хлопотливые обязанности хозяйки дома, и она то и дело отлучалась не кухню.
Кому сколько лет и кто на ком женат?
Решение
Решим задачу, составив и решив систему уравнений.
1. Каждая из жен младше мужа на 5 лет (по условшо 1), значит, в сумме их возраст должен составлять нечетное число, следовательно, Юлия не может быть женой Игоря (им в сумме 52 года (по условшо 3)) и Леонида (им в сумме 48 лет (по условию 5)). Следовательно, Юлия — жена Андрея.
2. Игорь старше Леонида на 4 года (это следует из условий 1, З и 5), значит, и жена Игоря старше жены Леонида на 4 года (это следует из условия 1). Следовательно, Игорь женат на Еве, Леонид на Марте.
З. В сумме всем
шестерым 151 год (по условию 4), а каждая жена младше мужа на 5 лет (по усло
1),
значит: Е + Ю + М + А + И + Л = Е + Ю +
+ М + (Е + 5) + (Ю + 5) + (М + 5) = 151; + ТО + + 2М = 151 - 15; + Ю + М) = 136. Тогда трем женам в сумме: Е + Ю + М = 68 (лет).
4. Ева — старшая из жен, она на 4 года старше Марты, следовательно, можно записать:
5. В то же время Юлии с Леонидом (мужем Марты) в сумме 48 лет, а Леонид, как и все мужья, старше жены Марты на 5 лет. Следовательно, можем записать:
ю + л- 48, 
м = 43, 
— ю - 43 - м.
6. Получили систему уравнений:
Е+Ю+М=68,
ю = 43 -м.
Решим ее:
М+4+43-М+М=68
м = 21 Е = 25 ю- 22.
Ответ: Игорь (30 лет) женат на Еве (25 лет), Леонид (26 лет) на Марте (21 год), Андрей (27 лет) на Юле (22 года).
Задача 101. Буфет
Шестеро друзей в ожидании электрички заскочили в буфет, в котором:
1) Маша купила то же, что Егор, и вдобавок еще бутерброд с сыром;
2) Аня купила то же, что Саша, но не стала покупать шоколадное печенье;
З) Кирилл ел то же, что Наташа, но без луковых чипсов;
4) Егор завтракал тем же, что и Наташа, но бутерброду с котлетой предпочел картофельные чипсы;
5) Саша ела то же, что Наташа, но вместо молочного коктейля пила лимонад.
Из чего состоял завтрак каждого из друзей?
146
Решение
Обозначим:
бутерброд с сыром — ВС; шоколадное печенье — П; луковые чипсы — ЛЧ; картофельные чипсы — КЧ; бутерброд с котлетой — БК; молочный коктейль — МК; лимонад — Л.
Далее будем рассуждать и ставить плюсы и минусы в таблицу.
1. Маша купила бутерброд с сыром, а Егор — нет (это следует из условия 1).
2. Егор купил картофельные чипсы, а не бутерброд с котлетой, Наташа бутерброд с котлетой, а не картофельные чипсы (это следует из условия 4).
З. Кирилл не ел луковые чипсы, а Наташа их ела (по условию З).
4. Саша не пила молочный коктейль, а пила лимонад; Наташа — наоборот (по условию 5).
5. Аня не купила шоколадное печенье, Саша — купила (это следует из условия 2).
6. Наташа ела то же, что Егор (по условию 4), а Егор не ел бутерброд с сыром (по доказательству), значит, Наташа не ела бутерброд с сыром.
7. Саша ела то же, что и Наташа (по условию 5), а Саша ела шоколадное печенье (по доказательству), значит, Наташа ела шоколадное печенье.
8. Наташа ела то же, что и Егор (по условию 4), а Наташа ела луковые чипсы, шоколадное печенье, пила молочный коктель и не пила лимонад (по доказательству), значит, Егор ел луковые чипсы, шоколадное печенье, пил молочный коктель, но не пил лимонад.
9. Маша ела то же, что и Егор (по условию 1), а Егор ел луковые чипсы, картофельные чипсы, шоколадное печенье, молочный коктель, Маша не пила лимонад и не ела бутерброд с котлетой (по доказательству), значит, ставим в таблицу в строку «Маша» те же
знаки, что и в строку «Егор», кроме первого столбца
10. Саша ела то же, что и Наташа (по условию 5), а Наташа ела бутерброд с котлетой, луковые чипсы и не ела бутерброд с сыром и картофельные чипсы (по доказательству), значит, Саша ела бутерброд с котлетой, луковые чипсы и не ела бутерброд с сыром и картофельные чипсы.
11. Кирилл ел то же, что и Наташа (по условию З), а Наташа ела бутерброд с котлетой, шоколадное печенье, пила молочный коктель, не ела бутерброд с сыром, картофельные чипсы и не пила лимонад (по доказательству), значит, ставим такие же знаки в строку «Кирилл» .
12. Аня ела то же, что и Саша (по условию 2), а Саша ела бутерброд с котлетой, луковые чипсы, пила лимонад и не ела бутерброд с сыром, картофельные чипсы и не пила молочный коктель (по доказательству), значит, ставим такие же знаки в строку « Аня».
Окончательно получим:
|
Имя |
|
|
|
Еда |
|
|
|
|
БС |
БК |
лч |
кч |
п |
мк |
л |
|
|
Маша |
|
|
|
|
|
|
|
|
Егор |
|
|
|
|
|
|
|
|
Аня |
|
|
|
|
|
|
|
|
Саша |
|
|
|
|
|
|
|
|
Кирилл Наташа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: см. таблицу.
Задача 102. Любители животных
Четыре семьи, дружившие между собой, держат по 10 различных животных. Их питомцы — белки, кролики, хомяки и ежи. Каждая семья держит разное число животных разных видов — от одного до четырех, и в разных семьях разное количество зверушек одного вида.
148
Определите, сколько и каких животных в каждой семье, если известно, что:
1) у Ивановых, Сидоровых и Петровых ежей не по два;
2) у Ивановых и Петровых кроликов, а у Кузнецовых кроликов и хомяков не по одному;
З) в семьях Сидоровых, Петровых и Кузнецовых живуг не по три белки;
4) в семьях Ивановых и Петровых хомяков не по два и не по четыре.
Решение
1. У Ивановых, Сидоровых и Петровых ежей не по 2 (по условию 1), значит, у Кузнецовых 2 ежа.
2. У Кузнецовых кроликов и хомяков не по одному (по условию 2) и не по 2 (по доказательству), значит, хомяков и кроликов может быть только З или 4. У Ивановых и Петровых кроликов не по одному (по условию 2), значит, по 2, З или 4.
З. В семьях Сидоровых, Петровых и Кузнецовых не по З белки (по условию З), значит, у Ивановых З белки.
4. В семьях Ивановых и Петровых не по 2 и не по 4 хомяка (по условию 4), а так как у Кузнецовых 2 ежа, у Кузнецовых 4 хомяка.
5. У Кузнецовых 4 хомяка и 2 белки (по доказательству), значит, у них З кролика (см. условие 2). Следовательно, белка у них одна, так как всего животных должно быть 10.
6.
У Ивановых, Петровых и Кузнецовых кроликов не по одному (по
условию 2), значит 1 кролик 
у Сидоровых.
7. У Ивановых и Петровых не по 2 хомяка (по условию 4), а у Кузнецовых 4 хомяка (по доказательству), значит 2 хомяка — у Сидоровых.
8. У Сидоровых 2 хомяка, а у Кузнецовых 4 хомяка (по доказательству), значит у Ивановых может быть З или 1 хомяк. Но у Ивановых З белки (по доказательству), а число разных животных должно быть разным. Значит, у Ивановых один хомяк. Тогда у Петровых — З хомяка.
9. У Сидоровых 1 кролик и 2 хомяка (по доказательству). У Ивановых — З белки (по доказательству). Значит, у Сидоровых белок может быть только 4 (животных в семье разное количество разных видов). Тогда у Сидоровых З ежа.
10. Белок у Ивановых З, у Сидоровых 4, у Кузнецовых — 1. Тогда у Петровых — 2 белки.
11. У Петровых не 1 кролик (условие 2), а у Кузнецовых — З кролика (по доказательству). При этом у Петровых 2 белки (по доказательству). Значит, у Петровых 4 кролика. Тогда у Ивановых — 2 кролика.
12. Животных каждого вида всего 10. Выполняя арифметические подсчеты, получим, что ежей: у Ивановых — 4, у Сидоровых — З, а у Петровых — 1. Окончательно получим:
|
Семьи |
|
Животные |
|
Итого |
|
|
Белки |
Кролики Хомяки |
Ежи |
|||
|
Ивановы |
з |
2 1 |
4 |
10 |
|
|
Сидоровы |
4 |
1 |
2 |
з |
10 |
|
Петровы |
2 |
4 |
з |
1 |
10 |
|
Кузнецовы |
1 |
з |
4 |
2 |
10 |
Ответ: у Ивановых З белки, 2 кролика, 1 хомяк, 4 ежа; у Сидоровых 4 белки, 1 кролик, 2 хомяка, З ежа; у Петровых 2 белки, 4 кролика, З хомяка, 1 еж; у Кузнецовых 1 белка, З кролика, 4 хомяка, 2 ежа.
Раздел З. Задачи на переправу
Трудность
задач на переправу связана с ограниченной грузоподъемностью плавательных
средств в условиях задач и с количеством и особенностями пассажиров.
Для записи хода решения таких задач используют схему, которую предлагается составлять следующим образом: схематично изображаются река, берега и плавательное средство; каждый этап переправы отделяется горизонтальной чертой; направление движения плавательного средства указывается стрелкой над обозначениями тех, кто переправляется на текущем этапе.
 |
Для учащихся 4—6 классов.
Задача 1. Поход
Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться на другой берег отцу и сыновьям?
Сколько времени (минимально) потребуется на переправу, если каждая поездка через реку занимает З минуты?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Первый сын (01) Второй сын (02) Отец (О) |
|
Надо: |
Как переправиться? 
Рассуждения:
|
Берег 1 |
Река |
Берег 2 |
|
С1 С20 |
|
|
|
о |
|
|
|
о |
01 |
|
|
|
о |
|
|
|
|
о |
|
|
|
о |
|
|
|
|
Ответ: на переправу потребуется 15 минут.
Задача 2. Отряд солдат
Отряд солдат подходит к речке, через которую необходимо переправиться. Но мост сломан, а река глубока. Вдруг командир замечает двух мальчиков, которые катаются на лодке недалеко от берега. Но лодка так мала, что на ней может переправиться только один солдат или только двое мальчиков — не больше! Однако все солдаты переправились через реку именно на этой лодке. Как это было сделано?
Решение
Аналогично решению предыдущей задачи, по предложенной выше схеме вместо отца каждый раз переправляется один из солдат, а затем оба мальчика возвращаются назад. Затем этот цикл повторяется для каждого очередного солдата.
Задача З. Волк, коза и капуста
Крестьянину нужно перевезти через реку волка, козу и капусту. Но лодка такова, что в ней может поместиться только крестьянин, или крестьянин только с волком,
или только с козой, или только с капустой. Но если оставить волка с козой одних, то волк съест козу, а если оставить козу одну с капустой, то коза съест капусту. Как крестьянин перевез свой груз?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Капуста (Ка) Волк (В) Коза (Ко) Крестьянин (Кр) |
|
Надо: Как переправиться? |
Рассуждения:
|
Берег 1 |
Река |
Берег2 |
|
В кр Ка ко |
|
|
|
В Ка |
кр ко |
|
|
В Ка |
|
ко |
|
в |
кр Ка |
ко |
|
в |
кр ко |
Ка |
|
ко |
крв
Кр
|
Ка |
|
ко |
В Ка |
|
|
|
В Ка |
|
|
|
|
В кр Ка ко |
Задача 4. Пожар в джунглях
В джунглях разгорелся пожар. Багира должна перенести котенка, лисенка и мышонка через пропасть. В какой последовательности она будет их переносить, учитывая, что котенок и лисенок охотятся за мышами?
Решение
Аналогично решению задачи З.
Задача 5. Три рыцаря и три оруженосца
Три рыцаря — Виктор, Ромул и Конунг каждый в сопровождении оруженосца Веньямина, Романа и Константина, съехались на берег реки, намереваясь переправиться на другую сторону. Им удалось найти маленькую двухместную лодку, и переправа произошла бы легко, ведь лошади могли перебраться вплавь. Но одно затруднение чуть было не помешало этому предприятию.
Все оруженосцы, словно сговорившись, наотрез отказались оставаться в обществе незнакомых рыцарей без своих хозяев. Не помогли ни уговоры, ни угрозы. Трусливые оруженосцы упорно стояли на своем.
И все же переправа состоялась, все шесть человек благополучно переправились на другой берег с помощью одной двухместной лодки. При этом было соблюдено условие, на котором настаивали оруженосцы. Как это было сделано при условии, что гребли только оруженосцы?
Решение
Эталон записи решения задачи в тетради
|
Дано: Рыцари (В, Р, К) Оруженосцы (в, р, к) Причем: в — оруженосец рыцаря В, р — оруженосец рыцаря Р, к — оруженосец рыцаря К |
|
Надо: Как переправиться? |
Рассуждения:
|
Берег 1 |
Река |
Берег 2 |
|
ВРКврк |
|
|
|
ВР Кк |
|
|
|
ВР Кк |
в |
|
|
РКк |
вв |
|
|
РКк |
|
в |
|
Ррк |
|
в |
|
Ррк |
|
вв |
|
|
|
вв |
|
|
к |
ввк |
|
|
|
ввк |
|
|
|
ВКРв |
|
|
|
ВКРв |
|
|
|
ВКРвкр |
Задача 6. Четыре рыцаря и четыре оруженосца
К реке подъехали четыре рыцаря с оруженосцами и обнаружили одну трехместную лодку. Могут ли они переправиться на другой берег при условии, чтобы, оказавшись отдельно от своего рыцаря, ни один оруженосец не находился при этом в обществе других рыцарей? Рыцари тоже согласились грести.
Решение
Эталон записи решения задачи в тетради:
|
Дано: рыцари (А, Б, В, Г) оруженосцы (А 1, Б1, В1, Г 1) |
|
Надо: Как переправиться? |
Рассуждения:
|
Берег 1 |
Река |
Берег 2 |
|
|
АБВГА1БIВ1Г1 |
|
|
|
|
АБВГА1 |
|
|
|
|
АБВГА1 |
|
|
|
|
АБА1Б1 |
вг |
|
|
|
АБА1Б1 |
АБВ |
|
|
|
|
|||
|
|
АБВГ |
||
|
|
|
АБВГ |
|
|
|
|
АБВГБIВ1 |
|
|
|
АБВГБ1В1 |
||
|
|
|
АБВГА1 Б1 Г1 |
Задача 7. Три капризные девочки
 |
Таким образом, неожиданно возникли дополнительные условия переправы, но ради забавы путники решили попытаться их выполнить. Как они действовали?
Решение
Данная задача похожа на задачу 5 про трех рыцарей и трех оруженосцев, но с отличием: в данной задаче грести могут все. Соответственно, получается другое решение.
Эталон записи решения задачи в тетради:
|
Дано: Отцы (А, Б, В) Дочери (А1, Б1, В1) Причем: А 1 — дочь А, — дочь Б, — дочь В |
|
Надо: Как переправиться? |
Задача 8. Четыре капризные девочки
Веселая компания (из предыдущей задачи) благополучно переправилась на противоположный берег реки и уселась отдыхать. Возник вопрос: можно ли было организовать переправу через реку на тех же условиях с помощью одной лодки четырех пар, если девочки откажутся грести? Выяснилось, что при сохранении условий, выдвинутых девочками, переправу можно было бы осуществить только при наличии лодки, поднимающей трех человек. Каким образом?
Решение
Аналогично задаче 6 с тем отличием, что гребут только четверо отцов.
Задача 9. Переправа через реку с островом
Наши путешественники (см. задачу 8) решили, что и на лодке, вмещающей только двух человек, можно осуществить переправу с одного берега на другой четырех девочек с их отцами, если посреди реки есть остров, на котором можно делать промежуточную остановку и высаживаться. В этом случае для окончательной переправы требуется совершить не менее девяти переездов. (Переездом считается переправа туда и обратно.) Найдите решение этой задачи, если предполагается, во-первых, как и в предыдущих задачах, что ни одна девочка не будет находиться ни в лодке, ни на острове, ни на берегу в обществе других отцов без своего отца и, во-вторых, что девочки еще настолько малы, что ни одна из них сама грести не может.
Решение
Эталон записи решения задачи в тетради:
Дано:
Отцы (А, Б, В, Г) Дочери (А1, Б1, В1, Г1)
Надо:
Как переправиться?
Задачи
Задача 10. Переправа через реку с островом
Четыре рыцаря с оруженосцами должны переправиться через реку на лодке, которая вмещает не более двух человек. Посреди реки есть остров, на котором можно высаживаться. Как совершить эту переправу так, чтобы ни на острове, ни в лодке ни один оруженосец не находился в обществе чужих рыцарей без своего хозяина?
Решение
Аналогично задаче 9 с тем отличием, что грести могут все.
Задача 11. Два путешественника и два разбойника
К реке, у берега которой находилась лодка, вмещающая только двух человек, подошли два разбойника и два путешественника. Разбойники не решались напасть на путешественников. Они могли бы совершить нападение, только если на берегу остались бы два разбойника и один путешественник. У одного из разбойников была сломана рука, и он даже не мог грести веслами. Как надо переправиться через реку разбойникам и путешественникам,чтобы последние избежали нападения?
Решение
Эталон записи решения задачи в тетради:
Задачи
Рассуждения:
|
Берег 1 |
Река |
Берег 2 |
|
|
|
|
|
|
112 Р2 |
|
|
|
п2 |
Р2 |
|
|
гп П2 |
|
|
|
|
|
|
|
|
|
|
|
|
ГП Р1112 Р2 |
При решении следующей
задачи необходимо обратить внимание на то, что не только важно переправиться
через реку, но и последовательность переправы должна быть такой, чтобы каждый
участник выполнил свои обязанности.
Задача 12. Поход с ночлегом
Таня, Коля и их отец отправились в поход.
К вечеру они вышли к реке, тихой и неглубокой. У берега был плот, выдерживающий
груз до 100 кг. Вес отца 
80 кг, Тани — 50 кг, Коли — 40 кг, рюкзака
— 15 кг. Переправившийся на противоположный берег Коля прежде всего должен
набрать хворост и развести костер, Таня — почистить картошку и рыбу для ухи,
отец 
поставить палатку для ночлега. Для
выполнения каждого из этих трех дел требуется 20 минут. Одна переправа через
реку занимает 10 минут. Как осуществить переправу, чтобы менее чем за полтора
часа все трое успели выполнить свои обязанности? При этом необходимо учесть,
что через час будет темно и в течение часа надо разжечь костер.
6-1703
Решение
Эталон записи решения задачи в тетради:
|
Дано: Таня (Т) — 50 кг Коля (К) — 40 кг Отец (О) — 80 кг Рюкзак (Р) — 15 кг |
|
Надо: Как переправиться и выполнить поручения? |
Рассуждения:
|
Берег 1 |
Река |
Берег2 |
Время, мин |
Обязанности |
|
ТКОР |
|
|
|
|
|
ОР |
тк |
|
10 |
|
|
ОР |
т |
|
20 |
20 мин костер |
|
о |
тр |
|
зо |
|
|
О |
|
тр |
|
|
|
|
о |
ТР |
50 |
|
|
|
т |
ОР |
60 |
20 мин палатка |
|
|
тк |
ОР |
70 |
|
|
|
|
Т КОР |
|
|
Задачи со сказочными
сюжетами очень нравятся детям. Являясь занимательными по форме, они усиливают
интерес, побуждают ребенка решать проблему, вызывают желание помочь
полюбившимся героям. Красота решения, неожиданный поворот мысли, логика
рассуждений все это усиливает эмоциональное восприятие детей.
Задачи
Однако условия задач со сказочными
сюжетами во многих случаях громоздки. Выбранная форма условия влечет за собой
относительно большой объем 
ведь очень часто при составлении задачи
приходится следовать литературному тексту сказки. Зато в таком случае дети с
большим удовольствием читают условие, вникают в его смысл, а работа над текстом
является существенной частью психологической подготовки ребенка.
Задача 13. Смекалка кузнеца Хечо
ЗОО лет тому назад жил злой, надменный князь. Была у князя дочь-невеста по имени Дариджан. Обещал князь свою Дариджан в жены богатому соседу, а она полюбила простого парня, кузнеца Хечо. Попытались было Дариджан и Хечо убежать в горы от неволи, но поймали их слуги князевы.
Рассвирепел князь и решил назавтра казнить обоих, на ночь же приказал запереть в высокую, мрачную, заброшенную недостроенную башню их, а вместе с ними еще и служанку Дариджан, девочку-подростка, которая помогала им бежать.
Не растерялся в башне Хечо, осмотрелся, поднялся по ступенькам в верхнюю часть башни, выглянул в окошко — прыгать невозможно, разобьешься. Тут заметил Хечо около окна забытую строителями веревку, перекинутую через заржавленный блок, укрепленный повыше окна. К концам веревки было привязано по пустой корзине. Хечо вспомнил, что при помощи этих корзин строители поднимали вверх кирпич, а вниз спускали щебень, причем если вес груза в одной корзине превышал вес груза в другой более чем на 5 кг, то корзина довольно плавно опускалась на землю; другая корзина в это время поднималась к окну.
Хечо на глаз определил, что Дариджан весит около 50 кг, служанка не более 40 кг. Свой вес Хечо знал около 100 кг. Кроме того, он нашел в башне цепь в 30 кг. В каждой корзине могли поместиться человек и цепь или даже 2 человека. Как они выбрались из башни?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Дариджан (Д) — 50 кг Хечо (Х) — 100 кг Служанка (С) — 40 кг цепь (Ц) — ЗО кг Корзина находится внизу
|
|
Надо: Как все выбрались из башни? |
Рассуждения:
|
Башня |
1-я корзина |
2-я корзина |
Земля |
||
|
содер- жимое |
Местонахождение |
Содер- жимое |
Местонахождение |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СХ |
|
|
|
|
|
|
сх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дх |
|
|
|
|
|
|
дх |
|
|
|
|
|
|
сдх |
В жизни
человеку часто приходится сталкиваться с проблемами, которые можно решить
несколькими способами.
Усвоив прием решения задач из данного раздела, учащийся и при рассмотрении других задач (и разных жизненных проблем) сумеет увидеть различные подходы к решению и уже не будет искать единственный способ выполнения задания, а постарается представить себе несколько вариантов решения и выбрать из них наиболее удобный.
Приведенные ниже задачи решаются с помощью
графа: в ходе решения задачи вычерчивается граф 
фигура, состоящая из
отдельных вершин, соединенных друг с другом. Сначала необходимо научить детей
решать задачу по готовому графу, далее — достраивать предложенный граф, а затем
уже переходить к заданиям по его самостоятельному построению. Для учащихся 3—6
классов.
Задача 1. Игрушки
У Юры два автомобиля, четыре медвежонка и три мяча. Он хочет выбрать из этих игрушек один автомобиль, одного медвежонка и один мяч. Сколько у него есть вариантов выбора?
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
мячи
медвежата
автомобили
Ответ: 24 варианта.
Задача 2. Мебельная мастерская
Мебельная
мастерская имеет три образца стульев 
с бордовой, серой и зеленой обивкой и два
образца столов — круглые и квадратные. Маша с отцом пришли
в магазин, им нужно купить стол со стульями.
Сколько вариантов
выбора у них есть? Закончите составление дерева и перечислите эти варианты.
Покажите путь, по которому можно выбрать стол круглой формы и стулья с зеленой
обивкой. зеленые синие бордовые стулья
столы
квадратный круглый
Ответ: 6 вариантов.
Задача З. Одежда
У Даши четыре блузки — красная, желтая, голубая и зеленая и две юбки синяя и оранжевая. Сколько у нее вариантов подбора костюма? Закончите составление дерева и раскрасьте его ветви в соответствии с цветами одежды.
юбки
зеленая голубая желтая красная
блузки
Ответ: 8 вариантов.
Задача 4. Меню
В школьной столовой на первое можно заказать щи, гороховый суп или борщ, на второе котлету или рыбу, а на третье — чай или морс. Сколько вариантов обеда можно получить из указанных блюд? Закончите
графов
составление дерева и покажите цветным карандашом путь, который соответствует обеду «гороховый суп, котлета, морс». морс чай
3-е блюдо
2-е блюдо
1-е блюдо
Ответ: 12 вариантов.
Задача 5. Полдник
У мамы две груши и три банана. Каждый день в течение пяти дней она дает сыну на полдник по одному фрукту. Сколькими способами она может это сделать? Со-
ставьте дерево и отметьте на нем путь: «груша — банан 
банан
— груша — банан» (группа — Г, банан — Б).
5-й день
4-й день
3-й день
2-й день
1-й день
Ответ: 10 способами.
Задача 6. Гирлянды
Имеются две красные и три зеленые гирлянды. Их соединяют последовательно для украшения актового зала. Сколько различных комбинаций соединений мож-
но получить? Закончите составление дерева и покажите на нем цепочку «красная — зеленая — зеленая — красная — зеленая».
5-я гирлянда
4-я гирлянда
3-я гирлянда
2-я гирлянда
1-я гирлянда
Ответ: 10 комбинаций.
Задача 7. Книжные полки
Сколько существует вариантов расположения
трех книг на пяти книжных полках при условии, что на каждой полке должно
находиться не более одной книги? Закончите составление дерева, обозначая полки,
на которых стоит книга, буквой «К», а пустые полки 
буквой «П».
5-я полка
4-я полка
3-я полка
2-я полка
1-я полка
Ответ: 10 вариантов.
Задача 8. Башни из кубиков
Сколькими способами можно построить башню из трех синих и двух желтых кубиков, если должны быть использованы все пять кубиков? Сделайте рисунки этих башен.
Ответ: 10 способами.
Задача 9. Грибы
Сколькими способами можно разделить 10 одинаковых грибов между двумя ребятами? Предполагается, что каждому достанется хотя бы один гриб. Ответ: 9 способами.
 |
Три поросенка — Ниф-Ниф, Нуф-Нуф и
Наф-Наф 
решили построить себе домики. Выбрали три
прекрасных места — у реки, на озере и на горе. Найдите все возможные варианты
размещения домиков с помощью дерева, закончив его составление, и с помощью
таблицы, дописав в нее недостающие строки. Сколько таких вариантов получилось?
Перечислите их.
гора
НаФ-НаФ
Нуф-Нуф
Ниф-Ниф
|
Ниф-Ниф |
Наф-Наф |
Нуф-Нуф |
|
|
О |
|
|
|
|
|
Ответ: 6 вариантов.
1) Ниф-НиФ — у реки, Нуф-Нуф — У озера,
Наф-Наф — на горе; 2) Ниф-Ниф — У реки, Нуф-Нуф — на горе,
Наф-НаФ — у озера; 3) Ниф-НиФ — у озера, НуФ-Нуф — У реки,
НаФ-Наф — на горе;
4) Ниф-Ниф — У озера, Нуф-Нуф — на горе,
Наф-Наф — у реки;
5) Ниф-Ниф — на горе, Нуф-Нуф — У реки,
Наф-НаФ — У озера;
6) Ниф-Ниф — на горе, Нуф-Нуф — у озера, Наф-Наф — У реки.
Задача 11. Фотография на память
Виталик, Дима и Сергей решили сфотографироваться все вместе. Сколькими различными способами они могут встать друг рядом с другом? Ответ: 6 способами.
 |
В классе хорошо поют и хотят участвовать в конкурсе песни четыре девочки — Света, Лиля, Марина и Наташа. Однако нужно выбрать только двоих. Сколькими способами это можно сделать? Ответ: 6 способами.
Задача 13. Остров Ро-ко-ко
На острове Ро-ко-ко живет племя, которое использует только три буквы «А», «Б» и «В». В словах они могут повторяться не более двух раз каждая. Сколько различных слов у жителей этого острова, если все их слова трехбуквенные? Ответ: 24 слова.
Задача 14. Урок танцев
На урок в танцкласс пришли слон, волк и лев. Партнершами для них были выбраны мышка, белочка и лисичка. Помогите учителю расставить их в пары, если белочка боится, что ее съест волк, а слон — что он раздавит мышку. Сколько вариантов составления пар есть у учителя танцев? Перечислите их.
Решение
|
Дано: Слон (С) волк (В) Лев (Лев) Мышка (М) Белочка (Б) Лисичка (Л) |
|
Надо: Найти все варианты пар. |
Рассуждения:
Рассуждения:
Изобразим на графе условия задачи.
Белочка боится, что ее съест волк, значит, белочка может танцевать только со львом или слоном. (Изобраэкаем на графе.)
Лисичка может танцевать и со слоном, и со львом, и с волком. (Изображаем на графе.)
 |
лев С Лев С В Лев в
- 
- „партнеры
- партнерши
Теперь рассмотрим различные варианты составления пар.
Вариант 1
Пусть белочка танцует со львом. Тогда мышка может танцевать только с волком, значит, лисичка танцует со слоном. (Зачеркиваем соответствующие линии на графе.)
Лев С Лев С В Лев В
- -партнеры
- - -партнерши
Получаем пары: лисичка слон, белочка лев,
мышка — волк.
Вариант 2
Пусть белочка танцует со слоном. Тогда лисичка может танцевать с волком или львом. Пусть в этом варианте она танцует со львом. Значит, мышка танцует с волком. (Зачеркиваем соответствующие линии на графе.)
Лев С Лев С В Лев в
---- ---партнеры
- -партнерши
 |
Вариант З
Как и в предыдущем варианте, пусть белочка танцует со слоном, но лисичка не со львом, а с волком. Значит, мышка танцует со львом, (Зачеркиваем соответствующие линии на графе.)
Лев С Лев С В Лев в
- 
-партнеры
- -партнерши
Получаем
пары: белочка слон, лисичка 
волк,
мышка — лев.
|
Ответ: З варианта: |
|
|
|
|
1) лисичка слон, мышка — волк; |
белочка |
|
лев, |
|
2) белочка слон, мышка — волк; |
лисичка |
|
лев, |
|
З) белочка слон, лисичка — волк. |
мышка |
|
лев, |
Задача 15. Урок английского языка
На уроке английского языка присутствуют шесть человек — Настя, Оля, Егор, Аня, Витя, Глеб. Учительница хочет рассадить ребят так, чтобы каждый мальчик обязательно сидел с девочкой. Какие варианты у нее есть, если Настя и Глеб хотят сидеть вместе?
|
Дано: Настя (Н) Оля (О) Егор (Е) Аня (А) Витя (В) Глеб (Г) |
|
Надо: Найти все варианты |
Рассуждения:
 |
Изобразим на графе условия задачи.
Настя хочет сидеть с Глебом (по условию), значит, Витя и Егор с ней сидеть не будут. Следовательно, каждый из них может сидеть либо с Олей, либо с Аней.
(Изображаем на графе.)
девочки
-мальчики
Теперь рассмотрим различные варианты составления пар.
Вариант 1
Глеб сядет с Настей (по условию). Пусть Витя сядет с Олей, тогда Егор сядет с Аней. (Зачеркиваем соответствующие линии на графе.)
Получаем пары: Глеб — Настя, Витя— Оля,
Егор 
Аня .
Вариант 2
Глеб сядет с Настей (по условию). Пусть Витя сядет с Аней, тогда Егор сядет с Олей. (Зачеркиваем соответствующие линии на графе.) Ответ: 2 варианта:
1) Глеб — Настя, Витя — Оля, Егор — Аня; 2) Глеб — Настя, Витя — Аня, Егор — Оля.
Задача 16. В лодочном походе
Ребята сидели на трех лодках и ожидали еще трех своих товарищей — Тараса, Федю и Игната, которые задержались, покупая для всех продукты. Когда опоздавшие подошли к реке, внимательно посмотрели, как распределились в лодках их друзья. Зная, что им надо сесть в разные лодки, они выразили такие пожелания:
Тарас: «Я хотел бы сесть в первую или во вторую лодку ».
Федя: «Мне хочется сесть в первую или в третью лодку» .
 |
Определите, сколько существует вариантов решения задачи, и перечислите их.
Ответ: 2 варианта:
1) Тарас
сядет в первую лодку, Федя 
в третью, Игнат — во вторую;
2) Тарас
во вторую лодку, Федя 
в первую, Игнат — в третью.
Задача 17. Экскурсия
Учащиеся собрались на экскурсию и высказали пожелания, чтобы в день экскурсии урок математики был первым или вторым, чтения вторым или третьим, природоведения первым или третьим. Можно ли удовлетворить пожелания учащихся? Если можно, то сколькими способами и какими?
Ответ: 2 варианта:
1) первый
урок математика, второй 
чтение, третий — природоведение;
2) первый
урок — природоведение; второй 
математика; третий — чтение.
18. Бальные танцы
В кружок бальных танцев пришли три девочки со своими братьями: Аня с Алешей, Соня с Сашей, Таня с Толей. Пожеланиями ребят было, чтобы брат с сестрой не танцевали в паре. Кто с кем должен танцевать? Перечислите варианты составления пар.
Ответ: 2 варианта:
1) Аня Саша,
Соня Толя, Таня 
Алеша;
2) Аня
— Толя, Соня — Алеша, Таня 
Саша.
Задача 19. Квартет
 |
осел и козел.
«Ударили в смычки, дерут, а толку нет». Тогда осел и козел
поменялись местами. «Расселись, начали квартет. Он все-таки на лад нейдет».
Таким образом, они перепробовали все возможные варианты. Медведь всегда
оставался на одном месте. Сколько всего было вариантов расположения
незадачливых музыкантов?
мартышка козел мартышка осел осел козел
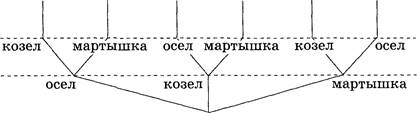
мишка Решение
Ответ: 6 вариантов.
Задача 20. Рамка
Из проволоки длиной 12 см согнули прямоугольную рамку. Длина и ширина этой рамки составляют целое число сантиметров. Сколькими способами можно получить рамку?
Ответ: З способами.
21. Трехзначные числа
Сколько трехзначных чисел можно составить из цифр 1, З, 5 при условии, что цифры в записи повторяться не будут? Перечислите эти числа.
Решение
Эталон записи решения задачи в тетради:
|
Дано: Цифры — 1, З, 5 |
|
Надо: Найти все трехзначные числа. |
 |
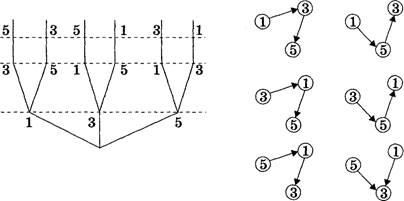
Ответ: 6 чисел 135, 153, 351, 315, 513, 531.
22. Скамейка
Три товарища — Алеша, Коля и Саша — хотят сесть на скамейку в один ряд. Сколькими способами они могут это сделать?
Ответ: 6 способами.
Задача 23. Лыжники
Аня, Боря, Вера и Гена —- лучшие лыжники школы. Надо составить команду из трех лыжников при условии, что Боря должен обязательно войти в данную команду. Сколькими способами можно составить команду?
Ответ: З способами.
Задача 24. Четырехзначные числа
Какие четырехзначные числа можно составить из цифр О и 1? Цифры могут повторяться.
Ответ: 8 чисел: 1000, 1001, 1010, 1011, 1100, 1101,
 |
Сколькими способами можно положить три цветных карандаша красный, желтый и синий друг рядом с другом?
Ответ: 6 способами.
Задача 26. Игрушки
Даны четыре игрушки кубик, машинка, рыбка и лодка. Сколькими способами их можно поставить друг рядом с другом? Решение
Дано:
Кубик (К)
Машинка (М) Рыбка (Р) Лодка (Л)
Надо:
Найти все способы.
Рассуждения:
 |
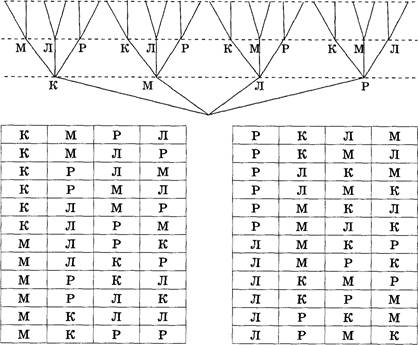
Ответ: 24 способами.
Задача 27. Рейсы самолетов
В связи с плохой погодой задерживаются три рейса самолетов — в Читу, Минск и Петрозаводск. Командиры самолетов высказали пожелания, чтобы рейс в Читу был первым или вторым, в Минск — вторым или третьим, в Петрозаводск — первым или третьим. Можно ли удовлетворить пожелания летчиков? Если да, то перечислите возможные варианты вылетов.
Ответ: 2 варианта:
1) первый рейс — в Читу, второй — в Минск, третий — в Петрозаводск;
2) первый
рейс — в Петрозаводск, второй 
в Читу, третий — в Минск.
Задача 28. Команды космических кораблей
Известно, что при составлении команд многоместных космических кораблей возникает вопрос о психологической совместимости участников космического путешествия. Даже вполне подходящие порознь люди могут оказаться непригодными для длительного совместного путешествия.
Предположим, что надо составить команду космического корабля из трех человек — командира, инженера и врача. На место командира есть четыре кандидата: а1, а2, аз, а4, на место инженера —- три кандидата: 61, 62, 63 и на место врача — три кандидата: с1, с2, сЗ.
 |
Перечислите все возможные варианты составления команды космического корабля, все члены экипажа которого психологически совместимы.
Решение
Рассуждения:
с2 сз с2 сз с1 с2 сз ст с2 сз
Алгоритм решения:
1. Построить граф, используя условия задачи о совместимости командиров кораблей с инженерами и врачами.
2. Провести анализ совместимости инженеров с врачами и вычеркнуть на графе линии, соответствующие несовместимости.
 |
Задача 29. Испытания Иванушки
«Задаю тебе задачу, сказала принцесса Иванушке. — Принеси мне из сада розу, найдя верный путь из этой комнаты. В следующую комнату можно пройти через одну из дверей: левую, правую или центральную. Такие же три двери будут перед тобой при переходе из этой, второй, комнаты в третью, а из третьей — в сад» . «Учти мои советы, — продолжила принцесса. — первый: из этого зала пройди через правую дверь. Второй: из второй комнаты через правую дверь не проходи. Третий: из третьей комнаты не проходи через левую дверь» .
Иванушка знал, что обычно из трех советов принцессы двум следовать нельзя. Кроме того, служанка принцессы успела шепнуть ему, что надо обязательно пройти через дверь каждого вида по одному разу.
Как и полагается в сказке, принес Иванушка розу и был вознагражден.
Какой же маршрут оказался единственно верным?
Ответ: путь Иванушки левая дверь, правая дверь, центральная дверь.
Задача 30. Загадка Бабы Яги
 |
По какому пути Иван Царевич должен пойти в царство Кощея?
Ответ: всего существует 9 возможных путей; самый короткий путь, когда Иван Царевич будет каждый раз выбирать среднюю дорогу.
Суть следующих задач
на выбор наиболее удобного способа действия заключается в том, что учащиеся
ставятся в более трудное положение: им нужно из нескольких верных ответов
выбрать наилучший, наиболее оптимальный. В рамках этого всегда творческого
задания дети находят удобное направление движения, самый короткий и удобный
путь до поставленной цели.
Задача 31. Путешествие Винни-Пуха
Винни-Пух решил навестить своих друзей: Пятачка, Кролика и Иа-Иа. Ему обязательно нужно побывать у каждого из своих друзей и вернуться домой. Если он к кому-то не зайдет, то его друг обидится. Но вы же знаете Винни-Пуха: он не любит длительных путешествий. Помогите ему выбрать кратчайший путь, если известно, как расположены домики друзей и на каком расстоянии они находятся друг от друга:
Винни-Пух
Иа-Иа
Пятачок
 |
|
Дано: Иа-Иа (И) Винни-Пух (В) Пятачок (П) Кролик (К) |
|
Надо: Найти кратчайший путь . |
Рассуждения:
в в в В в в
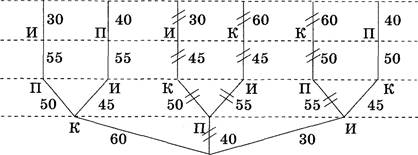
в
Алгоритм решения:
1. Построить граф, используя условие задачи, и расставить на нем расстояния.
2.
Определить пары симметричных вариантов (симметричные варианты —
это, например, пути В — К 
— п — и — в и в — и — п — к — В) и
вычеркнуть на графе один вариант из каждой пары.
З. Выписать оставшиеся варианты и подсчитать расстояния:
60 + 50 + 55 + зо = 195;
в— к —и— п— в = 60 + 45 + 55 + 40 = 200; в— и— к— п— в = зо +
45 + 50 + 40 = 165. Ответ: самый короткий путь Винни-Пуха: 
165.
Задача 32. Путешествие Пятачка
 |
Винни-Пух
Кролик
Ответ: самый короткий путь Пятачка:
п— в —и— к— п- 165 (либо симметричный путь:
165).
Задача 33. Космическое путешествие
На планету Земля из космоса пришли таинственные радиосигналы с предупреждением о начале сжатия нашей галактики Млечный Путь с последующим превращением ее в черную дыру, мощным взрывом и вспышкой сверхновой звезды.
После расшифровки удалось установить, что сигналы были посланы из созвездия Персея, туманности Андромеды и Магеллановых облаков.
 |
В каждый экипаж должны войти два юноши и две девушки. Отбор идет среди юношей — Юрия, Криса, Стива, Леонида, Эли и Ивана и девушек: Ольги, Джой, Наталии, Татьяны, Ребекки и Шарон.
Юрий, Леонид, Иван,
Ольга, Татьяна, Наталия 
русские, остальные — американцы.
Найдите варианты формирования экипажей, если известно, что:
1) в каждом космическом корабле должны быть двое русских и двое американцев;
2) Леонид
мечтает лететь вместе с Ольгой, Эли 
с Джой, Иван — с Ребеккой, Крис — с
Наталией;
З) Леонид и Эли готовятся к полету в созвездие Персея, Иван — к туманности Андромеды.
Решение
|
Дано: Три космических корабля Юноши: Юрий (Ю), крис Стив (С), Леонид (Л), Эли (Э), Иван Девушки: Ольга (О), джой (Д), Наталия (Н), Татьяна (Т), Ребекка (Р), Шарон (Ш) |
|
Надо: Найти все варианты с учетом заданных условий. |
 |
Алгоритм решения:
1. Построить граф, используя условия задачи по взаимной симпатии юношей и девушек и желание полететь в ту или иную звезную систему.
----- девушки
юноши корабли
|
«Пегас», |
«Пожиратель |
«Голубое |
|
туманность |
пространства» , |
пламя» , |
|
Андромеды |
созвездие |
Магеллановы |
|
|
Персея |
облака |
2. Провести анализ вариантов на графе.
Ответ: З варианта:
1) Иван, Ребекка, Юрий, Шарон летят к туманности Андромеды; Леонид, Ольга, Эли, Джой в созвездие Персея; Стив, Татьяна, Крис, Наталия — к Магеллановым облакам;
2) Иван, Ребекка, Стив, Татьяна летят к туманности Андромеды; Леонид, Ольга, Эли, Джой — в созвездие Персея; Юрий, Шарон, Крис, Наталия к Магеллановым облакам;
З) Иван, Ребекка, Крис, Наталия летят к туманности Андромеды; Леонид, Ольга, Эли, Джой — в созвездие Персея; Юрий, Шарон, Стив, Татьяна к Магеллановым облакам.
Задача 34. Озеленение района
 |
Найдите все варианты озеленения, если известно, что дуб плохо влияет на рост жасмина и сирени, а липа — на рост шиповника. Несовместимы: сосна и береза, сосна и липа, ель и дуб, ель и береза. Решение
Дано:
Три группы растений:
хвойные Деревья: ель (Е), сосна (С); лиственные Деревья: береза (Б), дуб (Д), липа (Л); кустарники: жасмин (Ж), сирень (С), шиповник (Ш).
Надо:
Найти все варианты с учетом заданных условий.
Рассуждения:
кустарники
лиственные
хвойные
Алгоритм решения:
1. Построить полный граф, отображающий все возможные варианты озеленения района по плану архитектора.
2. Провести анализ вариантов на графе с учетом совместимости зеленых насаждений. Ответ: З варианта:
1) ель — липа — жасмин;
2) ель — липа — сирень;
З) сосна — дуб — шиповник.
 |
Известно, что при составлении троек нападения в команде учитывается сыгранность и психологическая совместимость игроков. В команде по хоккею в основном три тройки нападения.
Надо составить из кандидатов тройки нападения, со-
стоящие из центрального нападающего, левого и правого крайних. На место центрального нападающего имеются кандидаты Ц1, Ц2, ЦЗ, на место левого крайнего кандидаты Л 1, Л2, ЛЗ, правого крайнего — П1, П2, ПЗ. Проверка показала, что Ц 1 хорошо совместим с Л1, .Л2, П2•, Ц2 — с Л1, П1, пз•, цз — с л, П2, пэ.
Решение Дано:
|
(Ц 1, Ц2, ЦЗ 1) ПЗ) |
|
учетом заданных условий. |
Три тройки нападения; центральные нападающие левые крайние (Л 1, Л2, ЛЗ) правые крайние (П 1, П2, Надо:
Составить все тройки с
Рассуждения:
гп П2 пз ш 112 пз гп
 |
1, Построить граф, используя условия задачи по составлению троек нападения.
2. Провести анализ вариантов на графе с учетом совместимости игроков.
Ответ: 6 вариантов:
3) Ц2 — Л1 — 111;
4) Ц2 — .J11 — ПЗ;
5) цз — лз — П2•,
6) цз — лез — пз.
 |
Задачи на перебор возможных вариантов решаются следующим образом:
выдвигается некая гипотеза, которая подтверждается или опровергается в ходе
дальнейших рассуждений. Гипотезы выдвигаются до тех пор, пока не найдется
единственный истинный вариант. Решение задач сопровождается записью
рассуждений, а там, где это необходимо для наглядности, еще и графической
иллюстрацией. В рассуждениях выдвижение гипотезы начинается со слова «Пусть».
Если при рассмотрении какой-то гипотезы получен ответ на вопрос задачи, то надо
обязательно проверить и другие варианты для подтверждения того, что найденное
решение является единственным истинным. Проверить гипотезу возможно с помощью
основ алгебры логики.
Для учащихся 6—11 классов.
Задача 1. Школа собаководства
Друзья усердно занимались в школе собаководства, тренируя своих питомцев — Джека, Лесси и Грифа, и вскоре приняли участие в соревнованиях.
Трое судей на вопрос друзей о результатах соревнований соответственно сказали:
1) Джек занял второе место;
2) Лесси заняла не второе место; З) Гриф не был первым.
После объявления результатов оказалось, что двое судей ошиблись, а один был прав.
Как распределились призовые места, если собаки заняли разные места?
Решение
Эталон записи решения задачи в тетради:
Дано:
Рассуждения:
Вариант 1
Пусть истинно высказывание о том, что Джек занял второе место.
Тогда высказывание о том, что Лесси заняла не второе место, должно быть ложно, значит, Лесси заняла второе место. Получили противоречие, так как Джек и Лесси не могли поделить второе место.
Значит, наше предположение о том, что первое высказывание истинно, неверно. Графическая иллюстрация:
д
1 л2
з противоречие
Вариант 2
Пусть истинно высказывание о том, что Лесси заняла не второе место.
Тогда высказывание о том, что Гриф не был первым, должно быть ложно, значит, Гриф занял первое место.
Гриф занял первое место (по доказательству), значит, Лесси и Джек заняли не первое место. Но из условия следует, что Лесси заняла не второе место. Значит, Лесси заняла третье место.
возможных 191
Из условия также следует, что высказывание о том, что Джек занял второе место, тоже должно быть ложно. Но он занял и не первое место (по доказательству). Следовательно, Джек занял третье место. Но он не мог поделить третье место с Лесси. Получилось противоречие.
Значит, наше предположение о том, что второе высказывание истинно, также неверно. Графическая иллюстрация:
д 1
з противоречие
Вариант З
Пусть истинно высказывание о том, что Гриф не был первым.
Тогда высказывание о том, что Джек занял второе место, должно быть ложно, значит, Джек занял не второе место.
Из условия также следует, что высказывание о том, что Лесси заняла не второе место, должно быть ложно. Значит, Лесси заняла второе место.
Лесси заняла второе место (по доказательству), значит, Гриф занял не второе место.
Гриф занял не первое (по условию) и не второе место (по доказательству), значит, Гриф занял третье место.
Гриф занял третье место (по доказательству), значит, Джек занял не третье место.
Джек занял не второе
и не третье место (по доказательству), значит, Джек занял первое место.
Графическая иллюстрация: д
преДположение верно
Ответ: Джек занял первое место, Лесси второе,
Гриф — третье.
Решение с помощью алгебры логики
В этой задаче высказывания обозначим так:
«Джек занял второе место» — Д2', «Лесси заняла не второе место» — Л2; «Гриф не был первым» — 111.
По условию задачи, после объявления результатов оказалось, что двое судей ошиблись, а один был прав. Это условие можно записать так:
По закону двойного отрицания имеем:
|
Выражение равно О, |
Выражение равно О, так |
|
так как Джек и Лесси |
как Гриф не может од- |
|
не могут одновременно |
новременно занимать |
|
занимать второе место (по условию). |
первое и второе места. |
Результат упрощения: Д2Л2Г1 = 1.
Изобразим результат графически:
-1
2
з
Из схемы видно, что Гриф мог занять
только третье место. Значит, Джек занял первое место.
Ответ: Джек занял первое место, Лесси второе, Гриф — третье.
Задача 2. Прогулка в парке
В парке гуляли дети, среди них три
подружки 
Аня, Валя и Люда. Одна из них была в
красном платье, другая — в белом, а третья — в синем. Когда их друзей спросили,
какое платье было на каждой из девочек, они ответили:
193
1) Аня была в красном платье;
2) Валя была не в красном платье; З) Люда была не в синем платье.
В каком платье была каждая из девочек, если извест-
но, что только одно утверждение в этих ответах истинно?
Решение:
Вариант 1
Пусть истинно высказывание о том, что Аня была в красном платье.
Анярасное
Валясинее
|
Люда |
белое |
противоречие
Вариант 2
Пусть истинно высказывание о том, что Валя была не в красном платье, тогда Люда единственная, кто может быть в красном платье, но она должна быть в синем (высказывание З должно быть ложно).
Анярасное
Валя- синее
Людбелое
противоречие
Вариант З
Пусть истинно высказывание о том, что Люда была не в синем платье.
предположение верно
Ответ: Люда была в белом платье, Аня в синем, Валя — в красном.
7-1703
Задача З. В магазине
Три подружки — Ксюша, Лена и Даша купили в магазине груши, яблоки и сливы, причем каждая девочка покупала только один вид фруктов и все покупки были разными. На вопрос, кто что купил, покупатели, стоящие в очереди, ответили:
1) Ксюша купила груши;
2) Лена купила не груши;
З) Даша купила не сливы.
Как оказалось позже, два из трех ответов были ложными и только один истинным.
Кто что купил?
Ответ: Ксюша купила сливы, Лена груши, Даша — яблоки.
Задача 4. День рождения
Три мальчика собрались идти на день рождения к своему другу и стали обсуждать вопрос о подарке. Вот часть их разговора.
Петя: «Давайте подарим ему книгу. Он любит книги, и у него их не меньше 100» .
Вася: «По-моему, у него их меньше 100» .
Коля: «Не знаю, сколько у него книг, но хотя бы одна книга у него есть» .
На дне рождения выяснилось, что из троих мальчиков был прав только один. Сколько книг было у именинника?
Ответ: прав был Вася. У именинника вообще нет книг.
Задача 5. Богатыри
Микула Селянинович узнал, что Змей Горыныч побежден. Победить его мог либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич. Вскоре Микуле Селяниновичу сообщили, что:
1) Змея Горыныча победил не Илья Муромец; 2) Змея Горыныча победил Алеша Попович.
Спустя некоторое время оказалось, что одно из этих сообщений истинно, а другое — ложно. Кто же победил Змея Горыныча?
195
Решение
Вариант 1
Пусть высказывание о том, что Змея Горыныча победил не Илья Муромец, истинно.
Тогда из условия следует, что высказывание о том, что Змея Горыныча победил Алеша Попович, ложно, т. е. его победил не Алеша Попович. Следовательно, Змея Горыныча победил Добрыня Никитич.
Вариант 2
Пусть высказывание о том, что Змея Горыныча победил Алеша Попович, истинно.
Тогда из условия следует, что высказывание о том, что Змея Горыныча победил не Илья Муромец, ложно, т. е. его победил Илья Муромец.
Получили противоречие, значит, наше предположение неверно.
Решение с помощью алгебры логики
В этой задаче высказывания обозначим так:
«Змея Горыныча победил не Илья Муромец» — им;
«Змея Горыныча победил Алеша Попович»
Запишем условие задачи: 1
Им Ап Им Ап = 1.
По закону двойного отрицания имеем:
им Ап Им Ап = 1.
Выражение равно О, так как Илья Муромец и Алеша Попович не могли одновременно убить Змея Горыныча.
Результат упрощения: Им Ап = 1.
Изобразим результат графически:
- Алеша Попович
Змей
Горыныч--
Илья Муромец
Добрыня Никитич
Из схемы видно, что Змея Горыныча победил Добрыня Никитич.
Ответ: Змея Горыныча победил Добрыня Никитич.
Задача 6. Кража
Инспектору Борисову стало известно, что совершена кража в ювелирном магазине. «Кто же мог на это пойти? » — задумался инспектор. Он знал, что это мог сделать либо вышедший недавно на свободу матерый уголовник по кличке Лось, либо появившийся в городе Аполлон Рубашкин, либо «начинающий» , но уже поднаторевший в преступном промысле Павел Смышляев. Вскоре инспектору Борисову поступила с разных сторон информация:
1) ювелирный магазин ограбил не Аполлон; 2) магазин ограбил Смышляев.
Спустя некоторое время оказалось, что одно из сообщений верно, а другое — ложно. Этого оказалось достаточным для того, чтобы Борисов установил, кто совершил кражу.
Кто это сделал?
Ответ: кражу совершил Лось.
Задача 7. Дорога к дедушке
Дедушка Вити работает лесником и живет в маленькой лесной деревушке под названием Солнечная полянка. Однажды захотелось Вите съездить на велосипеде к дедушке. Стал он просить маму:
— Разреши мне съездить к дедушке!
Говорит ему мама:
Ты заблудишься, сынок. На пути, по
которому тебе надо ехать к дедушке, есть перекресток, а от него расходятся три
дороги. И только одна из них ведет в Солнечную полянку, остальные же ведут в
дремучий лес. Надо знать, по какой из трех дорог следует ехать. Боюсь я тебя
одного отпускать!
— Пусти, мама! — просит ее сын, — я сумею найти дорогу!
Отвечает ему мама:
Ну хорошо, только обещай мне, если дорогу
не найдешь, то сразу возвращайся.
197
Обрадовался Витя и поехал сразу, пока мама не передумала. Едет и видит у перекрестка три дороги. Около каждой колышек со словами. Стал Витя надписи читать:
1) на первом колышке: «Эта дорога ведет в Солнечную полянку» ;
2) на втором колышке: «Эта дорога не ведет в Солнечную полянку» ;
З) на третьем
колышке: «Внимание! На одном из двух других колышков правда написана, а на
другом 
неправда. На мне — истина несомненная».
Остановился Витя на распутье. Помогите ему выбрать дорогу в Солнечную полянку.
Ответ: надо поехать по третьей дороге.
Задача 8. Экспедиция на Луну
Корреспонденту удалось узнать, что в составе экспедиции на Луну на должности командира корабля, физика и радиста назначены Сергеев, Матвеев и Алексеев. Он записал предположение, что командиром корабля будет Сергеев, Матвеев не будет физиком, а Алексеев командиром корабля быть не может. Позже выяснилось, что только одно из этих утверждений оказалось верным. Какие обязанности на корабле выполняли Сергеев, Матвеев и Алексеев?
Ответ: Сергеев — физик, Матвеев — радист, Алексеев — командир.
Задача 9. Кросс зверей
В лесу проводился кросс. Обсуждая его
итоги, одна белка сказала: «Заяц занял первое место, а второе 
лиса» .
Другая белка возразила: «Заяц занял второе место, а лось — первое». На что
филин заметил, что в высказывании каждой белки одна часть верная, а другая —
нет. Кто был первым, а кто вторым в этом кроссе?
Решение
Вариант 1
Пусть в высказывании первой белки первое утверждение «Заяц занял первое место» истинное.
Тогда второе «Лиса заняла второе место» — ложное,
т. е. лиса заняла не второе место.
8—1703
Тогда в высказывании второй белки первое утверждение «Заяц занял второе место» ложное, значит, второе утверждение «Лось занял первое место» истинное. Но по предположению первое место занял заяц.
Получили противоречие. Значит, наше предположение неверно.
Кратко можно записать:
Ы: заяц — 1 (И), лиса
Б2: заяц — 2 (Л), лось
Вариант 2
Пусть в высказывании первой белки истинно второе утверждение «Лиса заняла второе место» .
Тогда первое утверждение «Заяц занял первое место» ложное, т. е. заяц занял не первое место.
Так как по предположению лиса заняла
второе место, в высказывании второй белки первое утверждение 
«Заяц занял
второе место» ложное, значит, второе утверждение «Лось занял первое место»
истинное.
Получаем, что первое место занял лось,
второе 
лиса.
Кратко можно записать:
Б1: лиса — 2 (И), заяц — 1 (Л); Б2: заяц — 2 лось — 1
Решение с помощью алгебры логики
В этой задаче высказывания обозначим так:
«Заяц занял первое место» — 31 ;
«Лиса заняла второе место» — сих, «Заяц занял второе место» — 32 ; «Лось занял первое место» — лось1.
Запишем условие задачи:
Для высказывания первой белки: 31Л2 v 31Л2 — 1.
Для высказывания второй белки:
х./ 32J10Cb1 - 1 .
31Л2) Л 
32J10Cb1) - 1.
199
Перемножим скобки:
31J1232J10Cb1 х., 
31J1232J10Cb1—1.
Выражение Выражение Выражение равно О, так равно О, так равно О, так как заяц как лось и заяц как лиса и заяц не может занять не могут не могут одновременно одновременно одновременно первое занять первое занять второе и второе места. место. место.
Результат вычислений: 31Л2З2ЛOСЬ1 — 1.
заяц
-с: 1
лиса2 лосьз
Изобразим результат графически:
Ответ: первое место занял лось, второе — лиса.
Задача 10. Иностранные языки
Вадим, Сергей и Михаил изучают разные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны.
Какой язык изучает каждый из молодых людей?
Решение с помощью алгебры логики
В этой задаче высказывания обозначим так:
Вадим изучает китайский — Вк•,
Сергей не изучает китайский — Ск;
Михаил не изучает арабский — Ма.
В задаче известно, что только одно утверждение верно, а два других ложны.
Запишем формулу, которая правильно отражает условие задачи:
ВкСкМа Л вкскма Л ВкСкМа = 1.
Упростим выражение с учетом того, что по закону ДВОЙНОГО отрицания ск = Ск; Ма = Ма. Получим:
вкскма Л ВкСкМа Л вкскма = 1 .
|
Выражение равно О, так |
Выражение равно О, так |
|
как Михаил не может од- |
как Вадим и Сергей не |
|
новременно знать китай- |
могут одновременно знать |
|
ский и арабский языки. |
один и тот же язык. |
Результат вычислений: ВкСкМа = 1 . Изобразим результат графически:
Вадитуьарабский
Сергейяпонский
Михаилкитайский
Из схемы видно, что японский язык изучает Михаил, тогда арабский изучает Вадим.
Ответ: Сергей изучает китайский язык,
Михаил 
японский, Вадим — арабский.
Задача 11, Конкурс песни
Жюри распределило места в конкурсе песни.
Один из членов жюри
сказал: «Первое место я бы отдал песне «Поверь, мне тоже очень жаль», а второе 
песне
«Любочка».
Другой из членов жюри ответил: «Песне «Поверь, мне тоже очень жаль» я отдал бы второе место, а песне «Школьная пора» — первое».
Когда места были распределены, оказалось, что в каждом из высказываний членов жюри одна часть оказалась верной, а другая — нет.
Какие песни заняли первое и второе места в конкурсе? Ответ: первое место заняла песня «Школьная пора», второе — «Любочка» .
Задача 12. Чемпионат мира по футболу
Два футбольных болельщика спорили между собой о результате чемпионата мира, прошедшего восемь лет назад.
201
Первый болельщик говорил, что восемь лет назад чемпионом стала сборная Бразилии, а второе место заняла сборная Италии.
Второй болельщик говорил, что первое место заняла сборная Англии, а второе — сборная Бразилии.
На следующий день они снова встретились, уже зная, кто же был чемпионом, и один из них заметил: «Каждый из нас был прав в своем утверждении наполовину».
Можно ли установить, кто занял первое и второе места в чемпионате мира восьмилетней давности?
Ответ: первое место заняла сборная Англии, второе — Италии.
Задача 13. Необычная тетрадь
Однажды на лестнице была наидена странная тетрады В ней было записано 100 утверждений:
«В этой тетради ровно одно неверное утверждение».
«В этой тетради ровно два неверных утверждения» .
«В этой тетради ровно три неверных утверждения».
«В этой тетради ровно сто неверных утверждений» .
Есть ли среди этих утверждений верные и если да, то какие?
Решение
Каждые два утверждения в этой тетради противоречат друг другу. А это означает, что если в ней и найдется верное утверждение, то оно будет единственным. Если верно только одно какое-то утверждение, то девяносто девять ложны. И такое утверждение есть: «В этой тетради ровно девяносто девять неверных утверждений ».
Ответ: верное утверждение «В этой тетради ровно девяносто девять неверных утверждений».
Задача 14. Отдых в летнем лагере
Три ученика разных школ Новгорода приехали на отдых в один летний лагерь. На вопрос вожатого, в каних школах города Новгорода они учатся, каждый дал ответ .
Петя: «Я учусь в школе № 24, а Лена в школе
Вожатый, удивленный противоречиями в ответах ребят, попросил их объяснить, где правда, где ложь. Тогда ребята сознались, что в ответах каждого из них одно утверждение верно, а другое ложно. Вожатый подумал и сообразил, кто в какой школе учится.
Попробуйте и вы определить, учеником какой школы является каждый из ребят.
Решение
Вариант 1
1. Пусть утверждение Пети о том, что он учится в школе 24, истинно.
Тогда его утверждение о том, что Лена учится в школе N2 8, ложно.
2. Утверждение Пети о том, что он учится в школе № 24, истинно (по предположению), тогда утверждение Лены о том, что она учится в школе № 24, ложно, значит, истинно ее утверждение о том, что Петя учится в школе .N2 30. Но Петя учится в школе № 24 (по предположению),
Получили противоречие. Значит, наше предположение неверно, т. е. утверждение Пети о том, что он учится в школе № 24, ложно.
Петя- школа № 8
Лена-- школа № 24
Коляшкола № 30 противоречие
Графическая иллюстрация:
Вариант 2
1. Пусть утверждение Пети о том, что он учится в школе № 24, ложно.
Тогда истинно его утверждение о том, что Лена учится в школе 8.
203
2. Утверждение
Пети о том, что Лена учится в школе № 8, истинно (по предположению), тогда
утверждение самой Лены о том, что она учится в школе 
24, ложно, значит,
истинно ее утверждение о том, что Петя учится в школе № 30.
З. Утверждение Лены о том, что Петя учится в школе .N2 30, истинно, утверждение Коли о том, что Петя учится в школе № 8, ложно, а истинно его утверждение о том, что он сам учится в школе № 24.
Получаем, что Петя учится в школе .N2 30, Лена — в школе № 8, Коля — в школе № 24. Графическая иллюстрация:
Петя -школа № 8
Ленашкола № 24
Коляшкола № 30 преДположение верно
Решение с помощью алгебры логики
Приведенные в условии высказывания обозначим следующими переменными:
Высказывания Пети:
«Я учусь в школе № 24» — 1124.
«Лена учится в школе № 8» — Л8.
Высказывания Лены:
«Я учусь в школе № 24» — Ли.
«Петя учится в школе № 30» — Пзо
Высказывания Коли:
«Я учусь в школе .N2 24» — Ки.
«Петя учится в школе .N2 8» — П8.
Высказывание Пети можно записать так:
Формулы для высказываний второго и третьего учениксов:
липзо липзо - 1;
1.
Если из этих трех высказываний образовать логическое произведение, то оно должно быть истинным:
(П24Л8 1124.718) л (J12J130 липзо) л
л 
К24П8) = 1. (1)
Умножим сначала первую скобку на вторую. Получим:
|
Выражение рав- |
Выражение рав- |
Выражение рав- |
|
но О, так как |
но О, так как |
но О, так как |
|
Петя и Лена не |
Петя не может |
Лена не может |
|
могут учиться |
одновременно |
одновременно |
|
в одной школе. |
учиться в двух |
учиться в двух |
|
|
школах. |
школах. |
Исключая эти высказывания, получим:
Это уравнение умножим на третью скобку уравнения (1):
Перемножим скобки:
Выражение равно О, так как Лена и Петя не могут учиться в одной школе.
Результат вычислений: П24Л8Л24ПзоК24П8.
205
Графическая иллюстрация:
Петяшкола .N2 8
Ленашкола № 24
Коляшкола N2 30
Ответ: Коля учится в школе № 24, Лена -— в школе N2 8, Петя — в школе № 30.
Задача 15. Змеи
Ученые спорили, какая из змей самая опасная. Первый ученый сказал, что на первом месте по смертоносности укуса стоит очковая кобра, а на втором месте — габонская гадюка. Второй ученый сказал, что на первом месте — королевская кобра, на втором — очковая кобра. Известно, что в каждом из высказываний одна часть ложна, а другая истинна. Какая змея на каком месте по смертоносности укуса?
Решение
Эталон записи решения задачи в тетради:
|
Дано: Королевская кобра (К) Очковая кобра (О) Габонская гадюка (Г) |
|
Надо: Какая змея на каком месте? |
Рассуждения:
О
О
|
Вариант 1 |
|
|
1 у: О (истина) |
Г (ложь) |
|
2 у: К (истина) |
О (ложь) |
Вариант 2
1 у: О (ложь) Г (истина)
2 у: К (истина) О (ложь)
п преДположение верно
Ответ: на первом месте по
смертоносности укуса королевская кобра, на втором месте 
габонская гадюка.
Задача 16. Дежурные
В школе четырем дежурным старшеклассникам 
Андрееву,
Костину, Савельеву и Давыдову — поручили убрать седьмой, восьмой, девятый и
десятый классы. При проверке обнаружили, что десятый класс плохо убран. Стали
выяснять, кто какой класс убирал. Получили следующие ответы.
Андреев: «Я убирал седьмой класс, а Давыдов 
восьмой » .
Костин: «Я убирал
девятый класс, а Андреев 
восьмой» .
Савельев: «Я убирал
восьмой класс, а Костин 
десятый» .
Оказалось, что одна половина ответа каждого ученика была правильной, а другая — нет.
Кто убирал десятый класс?
Ответ: Десятый класс убирал Давыдов.
207
Задача 17. Дорога в театр
Мужчина спросил у встречных прохожих, как пройти в театр, и получил следующие ответы.
Первый прохожий сказал: «Сначала поверните направо, а потом идите прямо» .
Второй прохожий сказал: «Сначала поверните налево, а потом идите прямо» .
Третий прохожий сказал: «Сначала идите прямо, а потом поверните налево» .
Оказалось, что каждый из прохожих ошибся в одном направлении.
Как же надо было идти в театр?
Ответ: надо было все время идти прямо.
Задача 18. Что есть у Бори?
Боря учится в одном из старших классов. Надо узнать, в каком классе учится Боря и что он имеет, если каждое из приведенных ниже высказываний верно лишь наполовину.
1) Боря учится в 10 классе и имеет собственную лодку.
2) Боря учится в 9 классе, и никакой лодки у него нет.
З) Боря учится в 8 классе, и у него есть лодка и велосипед.
Ответ: Боря учится в 9 классе и имеет лодку и велосипед.
Задача 19. История с амфорой
Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый из них высказал по два предположения.
Алеша: «Это сосуд греческий и изготовлен в V веке».
Боря: «Это сосуд финикийский и изготовлен в III веке» .
Гриша: «Это сосуд не греческий и изготовлен в IV веке» .
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Решение с помощью алгебры логики
В условии нам даны высказывания школьников и учителя, где некоторые высказывания школьников
противоречат друг другу. Нам нужно найти истинное высказывание, отвечающее на поставленный в задаче вопрос.
Введем следующие обозначения:
«Это сосуд греческий» — G;
«Это сосуд финикийский» — Р;
«Сосуд изготовлен в III веке» — Уз; «Сосуд изготовлен в IV веке» — V4,• «Сосуд изготовлен в V веке» — У5.
Запишем в данных обозначениях условия задачи (формализуем ее).
Со слов учителя следует, что Алеша прав только в чем-то одном: или G = 1, или У5 = 1. Тогда тождественно истинным будет высказывание GV5 •v GV5.
Аналогично, из слов Бори и учителя следует:
FV3 FV3 = 1,
а из слов Гриши и учителя:
GV4 = 1.
Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия можно записать так:
V3V4V5 V3V4V5 V3V4V5 = 1,
Итак, мы получили пять тождественно истинных высказываний. Их нужно логически перемножить. Результат должен быть также тождественно истинным высказыванием:
1 = (GV5 х., GV5) л FV3) л (GV4 к., GV4) л л СО FG) л (V3V4V5 V3V4 V5) -
— {упростим: сначала перемножим первую и третью скобки и вторую и четвертую скобки} —
(GV50V4 GV5GV4 х., 
CV5GV4) л (FV3FO х., FV3FG
FV3FG ж., FV3FG) л (V3V4V5
3aAaT.1H Ha nepe60p B03MO'KHb1X BapøaHTOB 209
— {ynpocTHM Bblpa9KeHHfl B nepB0ü BTopoii CK06Kax,
YHHTb1Baa, qrro, Harrpm.aep, GG = O, GG = G, G G = G} = = (Gß5V4 v A (FV3Ö v A
{nepeMH0}KHM nepBY10 
CK06RM
ynpocTHM
110JryqeHHoe BblpææceHHe}
= (Gß5V4Fß3G v Gß5V4FV3G v
GV5V4Fß3C v GV5V4FV3G) A v v = (GFV3V4ß5 v 
v v =
GFV3V4V5V3V4ß5 v v GFV3V4V5V3V4V5 v v GFV3V4V5V3V4V5 v v
GFV3V4V5V3V4V5 v GFV3V4V5V3V4V5 = GFV3V4V5.
Pe3YJ1bTarr Bblt1HCJ1eHHiâ: GFV3V4V5 = 1. 3Haqwr, G 1,
H31'OTOBJ1eH B V Berce.
PeueHue Ha 983bLEe npoepa»wwupoeaHug Tlacrcanb
MeT0A COCTOHT B TOM, t1T06b1
nepe6paTb BCe zlonycT¼Mb1e 3HaT-reHHfl neperueHHb1x G, F, V3,
V4, 175 HaÜTH, 1-•caI-CHX HAX OCHOBHafl 
rrpHHHMaerr
3HaqeHHe 1 (HCTHHa). HT06b1 He YCJIŒKHflTb J101'1•rqeCKoe Bblpaycerme,
HC110J1b3YK)TCfl rra1-0Ke nepeMeHHb1e:
Fl = not F, Gl = not G, not V3, W4 = not V4, W5 — not V5•
program sosud; var 
Boolean;
begin write In ( 'G' •.7, 'V3' 
for G:=false
to true do for F: —false to true do for V3: —false to true do for V4 to
true do for V 5: —false to true do begin 
not 
not 
not 
not 
W5: not
Ä:=( (G and W5 or Gl and V 5) and (F and W3 or Fl and V 3) and (GI and W4 or G and V4)
and (F and Gl or Fl and G) and (V 3 and W4 and W5 or V4 and W 3 and W5 or V5 and W3 and w4) ) ; write (G.•7, F: 7, V3:7, v5:7, A: 7) ; if A true then write ( ' 0TBeT t : 15) ; write In end; read In end.
Pe3YJ1bTarr pa60Tb1 nporpaMMb1•.
0TBerr
CTpot1Ka, BblAeJ1eHHafl 
YCHPHb1M
1.11pHd)T0M, YRa-
3b1BaeT OTBeT.
Omeem: cocyA 
H31'OTOBJ1eH B V BeKe.
211
Задача 20. Сбор металлолома
Дима, Боря и Костя отправились собирать металлолом. Они нашли увесистую деталь, погрузили ее на тележку и повезли.
— Нам повезло, — сказал Дима по дороге. — Эта штука из чистой меди, да и весит килограммов тридцать.
— Какая там медь, — возразил Боря. — Это ржавое железо. Но ты не унывай. В нем сто килограммов будет.
Да, это явно
не медь, — вмешался Костя, — а весу пятьдесят килограммов, я думаю, наберется.
Оказалось, что каждый был прав только наполовину.
Что же нашли ребята и каков вес находки? Ответ: деталь из железа, весит 30 кг.
Задача 21. Карнавальные костюмы
На новогоднем карнавале самыми красивыми были признаны костюмы Ани, Вали, Гали и Димы. Это были костюмы феи, кота, паука и петуха. На вопрос, кто в каком костюме пришел на праздник, были даны следующие ответы.
— «Аня была в костюме феи, а Дима — в костюме петуха» ;
«Аня была в
костюме кота, а Валя в костюме 
феи » ;
— «Галя была в костюме феи, а Дима — в костюме паука» .
Дед Мороз сказал, что каждый ответ лишь наполовину правдив.
Кто в каком костюме был на карнавале, если все были в разных костюмах?
Решение
Вариант 1
1. Пусть в первом ответе его первая часть «Аня была в костюме феи» истинна. Тогда вторая часть «Дима был в костюме петуха» ложна.
2. Аня была в костюме феи (по предположению), тогда во втором ответе первая часть «Аня была в костюме кота» ложна, значит, истинна вторая часть «Валя была в костюме феи». Но в костюме феи была Аня (по предположению).
Получим противоречие, значит, наше предположение неверно.
Графическая
иллюстрация: Аняфея
Валякот Галя паук
Дима-------------петух противоречие
Вариант 2
1. Пусть в первом ответе его первая часть ответа «Аня была в костюме феи» ложна. Тогда вторая часть «Дима был в костюме петуха» истинна.
2. Дима был в костюме петуха (по предположению), тогда в третьем ответе вторая часть «Дима был в костюме паука» ложна, значит, истинна первая часть «Галя была в костюме феи».
З. Галя была в костюме феи (по доказательству), тогда во втором ответе вторая часть «Валя была в костюме феи» ложна, значит, истинна первая часть «Аня была в костюме кота» .
4. Дима был в костюме петуха, Галя —
феи, Аня 
кота, значит, Валя была в костюме паука.
Графическая иллюстрация:
Аня -
фея
Валя кот
Галя- паук
Димапетух предположение верно
213
Решение с помощью алгебры логики
В этой задаче высказывания обозначим так:
«Аня была в костюме феи» — Аф;
«Дима был в костюме петуха» — Дп;
«Аня была в костюме кота» — Ак;
«Валя была в костюме феи» — Вф',
«Галя была в костюме феи» — Гц;
«Дима был в костюме паука» — Да («а» 
вторая
буква в слове «паук»).
В условиях задачи сказано, что либо Аф
1, либо
Эту мысль можно выразить тождеством:
Аф
АфДп
Второе тождество: АкВф х./ АкВф 
Третье
тождество:
(1)
Если из полученных трех выражений образовать логическое произведение, то оно будет истинным:
(АфДп АфДп) Л (АкВф х., АкВф) Л (ГфДа РФ да) - 1.
Умножим сначала первую скобку на вторую, получим:
АфДпАкВф Х., АфДпАкВф АфДпАкВф - 1.
|
Выражение равно О, так |
Выражение равно О, так |
|
как Аня не может быть |
как Аня и Валя не могут |
|
одновременно в двух кос- |
быть одновременно в од- |
|
тюмах. |
ном и том же костюме. |
Исключая эти выражения, получим:
АДпАкВф АфЦпАкВф = 1. (2)
Уравнение (2) умножим на уравнение (1):
(АфДпАкВф АфДпАкВф) Л (ГфДа ГфДа) = 1;
АфДпАкВфГфДа
АфДпАкВфГфДа АфДпАкВфГфДа
АкВфГфДа - 1. 
|
Выражение рав- |
Выражение рав- |
Выражение рав- |
|
но О, так как |
но О, так как |
но О, так как |
|
Дима не может |
Дима не может |
Валя и Галя |
|
быть одновре- |
быть одновре- |
не могут быть |
|
менно в двух |
менно в двух |
одновременно в |
|
разных костю- |
разных костю- |
одном и том же |
|
мах . |
мах . |
костюме. |
Результат вычислений: АфДп АкВфГфДа = 1 .
Значит, Дима был в костюме петуха, Аня кота, Галя — феи. Следовательно, Валя была в костюме паука. Ответ: Аня была в костюме кота, Валя паука, Галя — феи, Дима — петуха.
Задача 22. Лукавые девушки
Четыре подруги — Маша, Полина, Ольга и Наташа — участвовали в соревнованиях по бегу и заняли первые четыре места.
Установите, кто какое место занял, если известно, что в каждом из приведенных ниже ответов, которые дали лукавые девушки опоздавшему к финишу корреспонденту, верной является лишь половина.
Наташа: «Ольга была второй, а Полина — первой».
Маша: «Нет, Наташа. Ольга была первой, а второй была ты» .
Ольга: «Да, что вы, девочки! Маша была третьей, а Полина прибежала четвертой».
Решение
Вариант 1
1. Пусть в ответе Наташи первое утверждение истинное, а второе — ложное, т. е. Ольга — вторая, а Полина не первая.
215
2. Ольга — вторая (по предположению), тогда в ответе Маши первое утверждение ложное, а второе истинное, т. е. Наташа — вторая. Но вторая — Ольга (по предположению).
Получили противоречие, значит, наше предположение неверно.
Графическая иллюстрация:
Маша-1 Полина-2 Ольгаз
Наташа4
противоречие
Вариант 2
1. Пусть в ответе Наташи первое утверждение — ложное, а второе — истинное, т. е. Ольга не вторая, Полина — первая.
2. Полина
— первая (по предположению), тогда в ответе Маши первое утверждение — ложное, а
второе 
истинное, т. е. Ольга не первая, Наташа —
вторая.
З. Полина — первая (по предположению), тогда в ответе Ольги второе утверждение — ложное, а первое — истинное, т. е. Маша была третьей. Тогда сама Ольга была четвертой.
Графическая иллюстрация:
Маша 1 
Полина2
Ольгаз
Наташа4 предположение верно
Решение с помощью алгебры логики
Обозначим высказывания следующим образом.
«Ольга была второй» — 02;
«Полина была первой» — 111;
«Ольга была первой» — 01',
«Наташа была второй» — Н2',
«Маша была третьей» —- Мз;
«Полина была четвертой» — П4.
В высказывании Наташи истинно либо 02, либо Щ. Это выражается так: 02111 v 02П1 = 1.
Рассуждая таким же образом, составляем логические тождества для высказываний второй и третьей девушек:
011-12 011-12 = 1,
МзП4 мзП4 = 1. (1)
Если из трех полученных высказываний образовать логическое произведение, то оно будет истинным:
(02111 02111) л (01Н2 01Н2) л (МзП4 МзП4) = 1,
Умножим сначала первую скобку на вторую:
0211101Н2
02П101Н2 х., 02П101Н2 
0211101H2 = 1.
|
но О, так как |
но О, так как |
но О, так как |
|
Ольга не может |
на втором месте |
на первом месте |
|
занять два места |
Ольга и Ната- |
Ольга и Поли- |
|
одновременно. |
ша одновременно |
на одновременно |
|
|
быть не могут. |
быть не могут. |
Выражение рав- Выражение рав- Выражение рав-
Исключая эти выражения, получим:
оп 2 1он - 1. (2)
217
Уравнение (2) умножим на уравнение (1):
02П101Н2 л (МзП4 мзП4) = 1;
02П1О1Н2М3П4 х., О2П1О1Н2М3П4 = 1.
Выражение равно О, так как Полина не может занять два места одновременно.
РезультАт вычислений: 02П1О1Н2МзП4 = 1. Тогда Полина на первом месте, Наташа — на втором, Маша — на третьем. Значит, Ольга заняла четвертое место.
Ответ: Полина заняла первое место, Наташа — второе, Маша — третье, Ольга — четвертое.
Задача 23. Участники математического кружка
Четыре участника математического кружка — Алексеев, Борисов, Васильев и Григорьев — учатся в разных параллельных классах. Им было предложено составить следующую задачу.
На вопрос «Из какого класса ты и твой друг?» каждый должен был дать ответ, одна часть которого правильна, а вторая — нет, но ответы должны быть такими, чтобы по ним можно было определить, кто в каком классе учится.
Мальчики дали следующие ответы.
Алексеев: «Я — из «А», а Васильев — из «В». Борисов: «Я — из «Б», а Васильев — из «Г».
Васильев: «Я — из «В», а Алексеев — из «Б».
Григорьев: «Я — из «А», а Алексеев — из «В».
Определите, в каком из параллельных классов учится каждый ученик.
Ответ: Алексеев учится в «Г», Борисов
Васильев — в «В», Григорьев
Задача 24. На пляже
На пляже в Сочи школьник Сергей познакомился с четырьмя мальчиками. На его вопрос, кто из какого города приехал отдыхать, они ответили:
Арташ: «Сурен из Еревана, Гураш из Тбилиси». Отар: «Сурен из Тбилиси, Арташ из Баку» .
9-1703
Сурен: «Арташ из Сочи, Отар из Тбилиси».
Все мальчики — из разных городов, и каждый из них прав наполовину.
Кто из какого города приехал отдыхать в Сочи?
Ответ: Сурен приехал из Еревана, Арташ из Баку, Отар — из Тбилиси, Гураш — из Сочи.
Задача 25. Диктант
Учитель проводил диктант по теме «Определения» . Каждый из учеников Коля, Сережа, Ваня, Толя и Надя — ошибся в одном из пяти заданий диктанта, причем все они ошиблись в разных заданиях. По окончании работы учащиеся высказались об ошибках, сделанных их одноклассниками.
Первый ученик: «Коля ошибся в первом задании, Ваня — в четвертом» .
Второй ученик: «Сережа ошибся во втором задании, Ваня — в четвертом» .
Третий ученик: «Сережа ошибся во втором задании, Коля — в третьем».
Четвертый ученик: «Толя ошибся в первом задании, Надя — во втором» ,
Пятый ученик: «Надя ошиблась в третьем задании, Толя — в пятом».
Определите, кто из ребят в КаКОМ задании допустил ошибку.
Решение
Вариант 1
1. Пусть в высказывании первого ученика утверждение «Коля ошибся в первом задании» истинное. Тогда утверждение «Ваня ошибся в четвертом задании» ложное.
2. В высказывании второго ученика утверждение «Ваня ошибся в четвертом задании» ложное, тогда утверждение «Сережа ошибся во втором задании» истинное.
З. В высказывании третьего ученика утверждение «Сережа ошибся во втором задании» истинное, тогда утверждение «Коля ошибся в третьем задании» ложное.
219
4. В высказывании четвертого ученика утверждение «Толя ошибся в первом задании» ложное, так как в первом задании ошибся Коля (по предположению). Тогда утверждение «Надя ошиблась во втором задании» истинное. Но во втором задании ошибся Сережа (по доказательству).
Получили противоречие, значит, утверждение о том, что Коля ошибся в первом задании, ложное.
Графическая иллюстрация:
Коля
Сережа
Ваня
Надя
Толя5 противоречие
Вариант 2
1. Пусть в высказывании первого ученика утверждение «Коля ошибся в первом задании» ложное.
Тогда утверждение «Ваня ошибся в четвертом задании» истинное.
2. В высказывании второго ученика утверждение «Ваня ошибся в четвертом задании» истинное, тогда утверждение «Сережа ошибся во втором задании» ложное.
З. В высказывании третьего ученика утверждение «Сережа ошибся во втором задании» ложное, тогда утверждение «Коля ошибся в третьем задании» истинное .
4. В высказывании пятого ученика утверждение «Надя ошиблась в третьем задании» ложное, так как в третьем задании ошибся Коля (по доказательству). Значит, утверждение «Толя ошибся в пятом задании» истинное.
5. В высказывании четвертого ученика утверждение «Толя ошибся в первом задании» ложное, так как Толя ошибся в пятом задании (по доказательству). Значит, утверждение «Надя ошиблась во втором задании» истинное.
Имеем: Ваня ошибся в четвертом задании, Коля 
в третьем,
Толя — в пятом, Надя — во втором. Значит, Сережа ошибся в первом задании.
Графическая иллюстрация: Коля1
Сережа -
2
Ваняз
Надя4
Толя5 преДположение верно
Решение с помощью алгебры логики
Обозначим высказывания следующим образом.
«Коля ошибся в первом задании» — 161 ;
«Ваня ошибся в четвертом задании» —
«Сережа ошибся во втором задании» — ф;
«Коля ошибся в третьем задании» — Ю;
«Толя ошибся в первом задании» — 7'1',
«Надя ошиблась во втором задании» — Н2', 
«Надя
ошиблась в третьем задании» — Нз; «Толя ошибся в пятом задании» — Т5.
В высказывании первого ученика либо IC1
1, либо
Это выражается так: К1В4 v ЕIВ4 — 1.
221
Рассуждая таким же образом, составляем логические уравнения для второго, третьего, четвертого и пятого одноклассников:
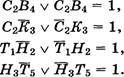(1)
Если из пяти полученных выражений образовать логическое произведение, то оно будет истинным: (k1B4 k1B4) л (С2В4 С2В4) л (С2К3 C2k3) л л (Т1Н2 Т1Н2) л (Н3Т5 нзТ5) = 1.
Умножим сначала первую скобку на вторую и получим:
|
Выражения равны О, так как Ваня не мог одновременно ошибиться и не ошибиться в одном и том же задании. |
= 1 |
Исключая эти выражения, получим:
(2)
Умножим теперь четвертую скобку на пятую. ПолуЧИМ:
Выражение равно О, так Выражение равно О, так как Толя не мог ошибить- как Надя не могла ошися в двух заданиях. биться в двух заданиях.
Исключая эти выражения, получим:
ТIН2Н3Т5 - 1. (3)
Уравнение (1) умножим на уравнение (2), получим:
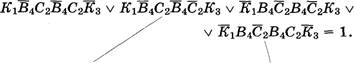
Выражение равно О, так Выражение равно О, так как Коля не мог ошибить- как Сережа не мог однося в двух заданиях. временно ошибиться и не ошибиться в одном и том же задании.
Исключая эти выражения и учитывая, что, напри-
мер, С2С2 = С2, В4В4 В4, получим:
(4)
Умножим» уравнение (З) на уравнение (4), получим:
|
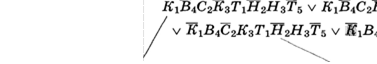
Выражение рав- |
Выражение рав- |
Выражение рав- |
|
но О, так как |
но О, так как |
но О, так как |
|
Коля и Толя не |
Коля и Надя не |
Надя и Сережа не |
|
могли одновре- |
могли одновре- |
могли одновре- |
|
менно ошибить- |
менно ошибить- |
менно ошибить- |
|
ся в одном и том |
ся в одном и том |
ся в одном и том |
|
же задании. |
же задании. |
же задании. |
Результат вычислений: К1В4С2КзТIН2НзТ5 = 1. Таким образом, Ваня ошибся в четвертом задании, Коля — в третьем, Надя — во втором, Толя — в пятом. Значит, Сережа ошибся в первом задании.
Ответ: Сережа ошибся в первом задании, Надя — во втором, Коля — в третьем, Ваня — в четвертом, Толя — в пятом.
Задача 26. Друзья
В поездке пятеро друзей — Антон, Борис, Вадим, Дима и Гриша — знакомились с попутчицей. Они предложили ей отгадать их фамилии, причем каждый из
223
них высказал одно истинное и одно ложное утверждение:
Дима сказал: «Моя фамилия Мишин, а фамилия Бориса — Хохлов». Антон сказал: «Мишин — это моя фамилия, а фамилия Вадима — Белкин» . Борис сказал: «Фамилия Вадима — Тихонов, а моя фамилия — Мишин». Вадим сказал: «Моя фамилия — Белкин, а фамилия Гриши — Чехов». Гриша сказал: «Да, моя фамилия Чехов, а фамилия Антона — Тихонов».
Какую фамилию носит каждый из друзей? Ответ: Антон Мишин, Вадим Тихонов, Дима Белкин, Борис Хохлов, Гриша Чехов.
Задача 27. Лыжный кросс
Учитель физкультуры объявил, что на следующем уроке он проведет соревнования по бегу на лыжах, и ребята высказали предположения о лучшей шестерке спортсменов класса. В предыдущем учебном году лучшими лыжниками класса считались Алешин, Иванов, Комаров, Соколов, Мамех и Токарев.
«Я думаю победа достанется Комарову, а Иванов будет только четвертым» , — сказал один мальчик.
«Я тоже думаю, что Иванов будет только четвертым, но победит Токарев» , — было мнение второго.
«Нет, Токарев будет пятым, а Мамех, пожалуй, выйдет на второе место» , — заявил третий ученик» .
Спор утих, но возник снова.
«Первое место — Соколову, а пятое место — Комарову», — сказал один из мальчиков.
«Нет, Комарову второе место, а третье
место 
Мамеху » , — возразил другой.
«На втором месте будет Алешин, а Комаров займет четвертое место», — завершил спор третий.
Оказалось, что шесть названных фаворитов в самом деле заняли в соревнованиях шесть первых мест, не разделив между собой ни одного места. Но в остальном каждое предсказание сбылось только наполовину.
Определите итоги соревнований.
Ответ: Соколов занял первое место, Алешин — второе, Мамех третье, Иванов — четвертое, Токарев — пятое, Комаров — шестое.
Задача 28. Сессия
Студент Лентяев, встретив в конце зачетной недели своих товарищей по группе, спросил их о том, какие экзамены и в какой очередности им придется сдавать. Ребята решили подшутить над Лентяевым и дали ему такие ответы.
Сергей: «Математику мы сдаем вторым экзаменом, а физику — третьим» .
Николай: «Нет, третьей мы сдаем историю, а последней — психологию» •
Петр: «Психология будет первым экзаменом, а вторым — история».
Федор: «Все-таки второй экзамен не математика, а четвертый — педагогика» .
Леонид: «Пятый экзамен у нас — физика, а психология — четвертая».
В своих ответах каждый из ребят лишь наполовину сказал правду, в чем они честно признались Лентяеву. После этого Лентяев, поразмыслив, установил точное расписание экзаменов.
Попытайтесь сделать это и вы.
Ответ: расписание сдачи экзаменов: первый экзамен психология, второй математика, третий — история, четвертый — педагогика, пятый — физика.
Задача 29. Ребята из разных городов
Пять школьников из пяти городов приехали в Смоленск для участия в областной математической олимпиаде. «Откуда вы, ребята?» — спросили мы их. Вот что ответил каждый.
Андреев: «Я приехал из Рославля, а Григорьев живет в Гжатске».
Борисов: «В Гжатске живет Васильев, а я прибыл из Вязьмы ».
Васильев: «Из
Рославля приехал я, а Борисов 
из Ельни» .
Григорьев: «Я прибыл
из Гжатска, а Данилов 
из Ярцева».
Данилов: «Да, я действительно из Ярцева, а Андреев живет в Вязьме».
225
Мы удивились
противоречивости их ответов. Ребята объяснили, что в каждом ответе одно
утверждение 
истинное, а другое — ложное. «Но наших
ответов достаточно, чтобы установить, откуда мы приехали», — заметили участники
олимпиады.
Попробуйте определить, откуда приехал каждый школьник.
Ответ: Андреев приехал из Рославля,
Борисов 
из Ельни, Васильев — из Гжатска, Григорьев
— из Вязьмы, Данилов — из Ярцева.
Задача 30. Формула-1
Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
«Вот увидишь, Шумахер не придет первым, — сказал Джон. — Первым будет Хилл».
«Да нет же, победителем будет, как всегда, Шумахер» , — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым» .
Питер, к которому обратился Ник, возмутился: «Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину» .
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение
Введем обозначения для логических высказываний:
«Победит Шумахер» — Ш;
«Победит Хилл» — Х;
«Победит Алези» — А.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займет этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Из высказывания Джона «Первым будет Хилл» следует, что Шумахер не придет первым. То есть первую часть высказывания Джона можно не учитывать. Аналогично для высказывания Ника.
Зафиксируем высказывания каждого из друзей: Джон: Х; ник: Ш; Питер: Х.
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание:
хшх ХШХ хш х = хш ХШ -
То есть Шумахер победил.
Ответ: победителем этапа гонок стал Шумахер.
Задача 31. Кто разбил стекло?
Один из пяти братьев — Андрей, Витя, Дима, Толя или Юра — разбил окно.
Андрей сказал: «Это сделал или Витя, или Толя».
Витя сказал: «Это сделал не я и не Юра».
Дима сказал: «Нет, один из них сказал правду, а другой — неправду» .
Юра сказал: «Нет, Дима, ты не прав».
Их отец, мнению которого можно доверять, уверен, что не менее трех братьев сказали правду.
Кто из братьев разбил окно? Кто сказал неправду? Решение
1. Высказывания Димы и Юры не могут быть одновременно истинными или ложными в силу своего смысла, значит, если одно из них истинно, то другое ложно.
2. Не менее трех братьев сказали правду (по условию), значит, правдивыми могут быть утверждения Андрея, Вити, Димы или Андрея, Вити, Юры.
З. Высказывание Вити в любом случае истинно, значит, окно разбил не он и не Юра.
4. Высказывание Андрея также в любом случае истинно, а мы уже знаем, что окно разбил не Витя, значит, его разбил Толя.
5. Мы установили, что Андрей и Витя сказали правду, значит, неправду сказал Дима (из смысла его высказывания).
Ответ: окно разбил Толя; неправду сказал Дима.
227
Задача 32. Кто испек пирог?
Один из пяти братьев — Никита, Глеб, Игорь, Андрей или Дима — испек маме пирог. Когда она спросила, кто сделал ей подарок, братья ответили следующее.
Никита: «Пирог испек Глеб или Игорь» .
Глеб: «Это сделал не я и не Дима».
Игорь: «Вы оба шутите».
Андрей: «Нет, один из них сказал правду, а другой обманул» .
Дима: «Нет, Андрей, ты не прав».
Мама знает, что трое из сыновей всегда говорят правду.
Кто испек пирог?
Ответ: пирог испек Игорь.
Задача 33. Кто принес букет цветов?
Кто-то принес букет цветов. Ребята стали гадать и высказали предположения, что букет принесли:
1) Андрей или Борис;
2) Андрей или Сергей; З) Борис или Даша; 4) Борис или Володя; 5) Володя или Галя; 6) Галя или Даша.
Учительница сказала, что в одном из этих предположений одно имя названо правильно, а второе — неправильно. Во всех же остальных предположениях оба имени названы неправильно. Кто принес цветы?
Решение
Если в каком-то предположении одно из имен названо правильно, то оно не может повторяться ни в одном из остальных предположений, так как в них все имена названы неправильно.
Единственное неповторяющееся имя это Сергей. Значит, именно он и принес цветы. Ответ: букет цветов принес Сергей.
Задача 34. Кто дежурный?
Староста назначил двух дежурных, но он заболел, и ребята не знали, кто должен дежурить. В результате класс остался неубранным. Когда стали выяснять, кто
должен был убрать класс, было высказано семь предположений о паре дежурных:
1) Сергей и Даша;
2) Даша и Андрей; З) Борис и Даша; 4) Галя и Борис;
5) Галя и Сергей;
6) Коля и Володя;
7) Борис и Володя.
Учительница сказала, что в первых пяти предположениях одно из имен названо верно, второе неверно, а в двух последних оба имени названы неверно.
Кто должен был дежурить?
Ответ: дежурить должны были Даша и Галя.
Задача 35. Уголовная история
У учительницы одной из начальных школ Нью-Йорка пропал кошелек. Украсть кошелек мог только один из пяти учеников — Лилиан, Джуди, Девид, Тео или Маргарет. При опросе этих детей каждый из них дал три показания.
Лилиан:
«Я не брала кошелек. (1)
Я никогда в своей жизни ничего не воровала. (2) Это сделал Тео». (З)
Джуди:
«Я не брала кошелек. (4)
Мой папа достаточно богат, и я имею свой собственный кошелек. (5)
Маргарет знает, кто это сделал». (6)
Девид:
«Я не брал кошелек. (7)
С Маргарет я не был знаком до поступления в шко-
Это сделал Тео». (9)
Тео:
«Я не виновен. (10)
Это сделала Маргарет. (11)
Лилиан лжет, утверждая, что я украл кошелек». (12)
229
Маргарет:
«Я не брала кошелек у учительницы. (13)
В этом виновата Джуди. (14)
Девид может поручиться за меня с рождения». (15)
При дальнейшем расследовании каждый из учеников признал, что в одном из своих показаний он солгал. Кто украл кошелек?
Решение
1. Предположим, что высказывание З — истинно, тогда высказывания 10 и 12 — ложные, значит, Тео солгал дважды, что невозможно по условию задачи. Следовательно, высказывание З — ложное, т. е. кошелек украл не Тео.
2. Высказывание З ложное, тогда и высказывание 9 ложное, значит, высказывание 8 истинное. Но тогда высказывание 15 ложное, следовательно, высказывание 14 истинное. То есть кошелек украла Джуди.
Ответ: кошелек украла Джуди.
Задача 36. Найдите преступника
Шорти Финелли был найден убитым, полиция арестовала по подозрению в убийстве троих: Бака, Джо и Тилпи. На допросе задержанные дали следующие показания.
Бак: «Я не убивал. Я никогда не видел Джо раньше. Я знаю Шорти» .
Джо: «Я не убивал. Бак и Тилпи мои приятели. Бак никогда никого не убивал» .
Тилпи: «Я не убивал. Бак лжет, говоря, что он никогда раньше не видел Джо. Я знаю, кто из двух других подозреваемых — убийца» .
Известно, что одно из высказываний каждого из задержанных ложно и один из подозреваемых — убийца. Кто убийца?
Решение
Вариант 1 
Пусть убийца — Тилпи.
Тогда его утверждение «Я не убивал»
ложно. Но если убийца — он, то его утверждение, что убийца 
один из двух других подозреваемых, тоже ложно. Тогда в утверждении Тилпи два ложных высказывания, что невозможно.
Получили противоречие. Значит, наше предположение, что Тилпи — убийца, неверно.
Графическая иллюстрация:
1.
«Я не убивал».
2. «Бак лжет, говоря, что он никогда Тилпираньше не видел Джо» .
-3. «Я знаю, кто из двух других подозреваемых — убийца».
противоречие
Вариант 2
Пусть убийца Бак, и его первое показание ложно.
Тогда истинны его высказывания «Я никогда не видел Джо раньше» и «Я знаю Шорти». Но в этом случае в показании Джо получится два ложных высказывания: «Бак и Тилпи мои приятели» и «Бак никогда никого не убивал».
Снова получено противоречие. Значит, наше предположение неверно.
Графическая иллюстрация:
1. «Я не убивал».
Бак
2. «Я никогда не видел Джо раньше» .
|
З. «Я знаю Шорти» |
|
|
|
. 1. «Я не убивал». |
|
джо=-_ |
2. «Бак и Тилпи — мои приятели». |
«Бак никогда никого
не убивал». противоречие
231
Вариант З
Тогда убийца — Джо. Остается проверить, что все остальные высказывания удовлетворяют условию задачи.
Джо: «Я не убивал» (ложь), «Бак и Тилпи — мои приятели» (истина), «Бак никогда никого не убивал» (истина).
Тогда:
Бак: «Я не убивал» (истина), «Я никогда не видел Джо раньше» (ложь), «Я знаю Шорти» (истина).
Тилпи: «Я не убивал (истина), «Бак лжет, говоря, что он никогда раньше не видел Джо» (истина), «Я знаю, кто из двух других подозреваемых -— убийца» (ложь).
Противоречия нет. Наше предположение подтвердилось.
Графическая иллюстрация:
1, «Я не убивал».
Бак- 2. «Я
никогда не видел Джо раньше» .
З. «Я знаю Шорти».
1. «Я не убивал».
Джо
2. «Бак и Тилпи — мои приятели».
З. «Бак никогда никого не убивал».
1. «Я не убивал».
Тилпи2. «Бак лжет, говоря, что он никогда раньше не видел Джо» .
«Я знаю, кто из двух
других подозреваемых — убийца».
преДположение верно
Ответ: убийца — Джо.
Задача 37. Суд идет
Перед судом стоят три человека, из которых только один может быть преступником. Известно, что преступник, отвечая на вопросы, всегда лжет. А те, кто не совершал преступления, всегда говорят правду.
Получив ответ одного из подозреваемых на вопрос «Виновны ли вы?» , судья задал двум другим один и тот же вопрос «Прав ли первый?» и получил следующие ответы.
Второй подозреваемый ответил: «Первый прав». Третий подозреваемый ответил: «Первый солгал». Кто же преступник?
Решение
На первый вопрос к первому подозреваемому может быть только один ответ «Нет, не виновен» . Если этот человек — преступник, он лжет, если невиновен, — говорит правду.
Вариант 1
Пусть первый подозреваемый говорит правду — он не виновен. Тогда второй подозреваемый говорит правду, а третий лжет. Значит, он и есть преступник.
Вариант 2
Пусть подозреваемый лжет — на самом деле он виновен. Тогда второй подозреваемый тоже лжет, а третий говорит правду. Данное решение противоречит условию задачи, так как лгут сразу двое.
Значит, наше второе предположение неверно.
Ответ: преступник — третий подозреваемый.
Задача 38. Найдите рыцаря
На острове Неизвестность живут рыцари и лжецы. Рыцари говорят только правду, лжецы — только ложь.
Незнакомец встретил трех жителей А, В и С этого острова, разговаривающих между собой. Он спросил у А: «Вы рыцарь или лжец?» Тот ответил, но неразборчиво, ничего нельзя было понять. Тогда незнакомец спросил у В: «Что сказал А?» «А сказал, что он лжец», — ответил В. «Не верьте В! Он лжет!» вмешался в разговор С.
Кто из островитян В и С рыцарь и кто — лжец?
233
Решение
На вопрос «Вы рыцарь или лжец?» и рыцарь, и лжец ответят одинаково: «Я — рыцарь». Поэтому В солгал, значит, С сказал правду. Следовательно, В — лжец, С — рыцарь.
Ответ: В — лжец, С рыцарь.
Задача 39. Школьный буфет
В очереди в школьный буфет стоят Вика, Соня, Боря, Денис и Алла.
Известно, что:
1) Вика стоит впереди Сони, но после Аллы;
2) Боря и Алла не стоят рядом;
З) Денис не находится рядом ни с Аллой, ни с Викой, ни с Борей.
В каком порядке стоят ребята?
Решение
Девочки стоят в таком порядке: Алла, Вика, Соня (по условию 1).
Боря по отношению к девочкам может стоять либо между Викой и Соней, либо после Сони (по условию 2).
Вариант 1
Пусть Боря и девочки стоят в таком порядке: Алла, Вика, Боря, Соня. Тогда Денис может стоять только после Сони, с краю (по условию З). И этот вариант удовлетворяет всем условиям задачи.
Вариант 2
Пусть Боря и девочки стоят в таком порядке: Алла, Вика, Соня, Боря. Тогда для Дениса в этой очереди нет такого места, которое удовлетворяло бы условию З. Значит, данное предположение неверно.
Эталон записи решения задачи в тетради:
|
Дано: Боря (Б) Соня (С) Вика (В) Денис (Д) Алла (А) |
|
Найти: В каком порядке стоят ребята? |
Рассуждения:
АВС
А ВБС А ВСБ
А ВБ С Д места для Д нет
верное предположение противоречие
Ответ: ребята стоят в следующем порядке: Алла, Вика, Боря, Соня, Денис.
Задача 40. Очередь к врачу
Пятеро друзей — Сергей, Михаил, Петр, Тимофей и Федор — сидят в очереди к зубному врачу.
Известно, что:
1) Сергей войдет к врачу раньше, чем Тимофей, но позже, чем Петр;
2) Федор и Петр не сидят в очереди рядом;
З) Михаил не сидит рядом ни с Петром, ни с Сергеем, ни с Федором.
В какой последовательности друзья будут лечить зубы?
Ответ: первым к врачу пойдет Петр, затем Сергей, Федор, Тимофей, Михаил.
Задача 41. Беседа подружек
На улице, встав в кружок, беседуют четыре подружки: Ася, Катя, Галя и Нина. Девочка в зеленом платье (не Ася и не Катя) стоит между девочкой в голубом платье и Ниной. Девочка в белом платье стоит между девочкой в розовом платье и Катей.
В платье какого цвета одета каждая девочка?
Ответ: Галя — в зеленом платье, Нина — в розовом,
Ася — в белом, Катя — в голубом.
235
Задача 42. Фигуры
На столе лежат в ряд четыре фигуры: треугольник, ромб, круг, квадрат. Цвета этих фигур — зеленый, желтый, синий, красный. В каком порядке лежат фигуры и какой цвет имеет каждая из них, если фигура красного цвета лежит между зеленой и синей фигурами, справа от желтой фигуры лежит ромб, круг лежит правее треугольника и ромба, причем треугольник лежит не с краю, и, наконец, фигура синего цвета не лежит рядом с фигурой желтого цвета?
Решение 
1. Красная фигура лежит между двумя фигурами (по условию), т. е. не с краю:
2. Желтая
фигура при этом лежит с краю, иначе она окажется рядом с красной фигурой, что
противоречит условию (красная фигура между зеленой и синей). Причем справа от
желтой фигуры есть еще фигура — ромб (по условию), поэтому желтая фигу
—
первая слева.
З. Красной фигуре остается третье место, синей — четвертое (так как синяя не должна быть рядом с желтой, по условию), а зеленой — второе.
4. Ромб — зеленый (так как он, по условию, справа от желтой
фигуры). Треугольнику достается третье место (только оно еще осталось не с
краю), а кру
последнее (он правее треугольника по
условию). Значит, квадрату остается первое место. а пав
Ответ: первым слева лежит желтый квадрат, следом — зеленый ромб, красный треугольник и синий круг.
Раздел б.
Занимательные задачи
Арифметические
задачи заслуживают особого внимания. Большинство учащихся не любят решать даже
простые задачи арифметическим способом. В то же время поиск таких решений
требует подчас весьма остроумных рассуждений, умения глубоко вникнуть в
ситуацию. Существует множество занимательных задач, которые достаточно быстро и
легко можно решить с помощью возможностей электронных таблиц.
Для учащихся 8—11 классов.
Задача 1. Хитрая лиса
В первую минуту лиса выбросила с воза 1
рыбку, во вторую минуту 2 рыбки, в третью минуту 
4 рыбки, в четвертую
минуту — 8 рыбок и т, д. Сколько всего рыбок выбросила лиса за 10 минут?
Решение
Обозначим:
i — номер минуты;
S — общее количество выброшенных рыбок.
Алгоритм:
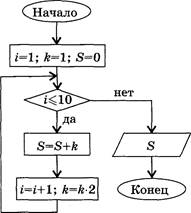
237
в электронных таблицах:
|
|
|
в |
||
|
1 |
Номер минуты |
Кол-во рыбок |
||
|
2 |
1 |
1 |
||
|
з |
|
|
||
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
Количестворыбок за 1 О минут |
-СУММ (В2:В11) |
||
Стрелки означают, что надо копировать формулы вниз до строки 11.
Результат — в ячейке В12.
Задача 2. Изумруды
У царя было семь
сыновей. В сундуке лежали изумруды. Затем пришел первый сын и взял половину
того, что было. Пришел второй сын и взял половину того, что осталось, и т. д.:
каждый из сыновей приходил и забирал половину того, что осталось. Наконец,
пришел последний, седьмой сын и увидел почти пустой сундук 
с двумя
изумрудами.
Сколько изумрудов лежало в сундуке первоначально?
Решение
Обозначим:
— номер сына;
S — общее количество изумрудов.
Алгоритм:
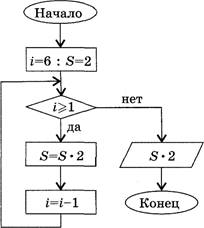
Решение в электронных таблицах:
|
|
|
в |
||
|
1 |
Номер сына |
Кол-во изумрудов |
||
|
2 |
7 |
2 |
||
|
з |
=А2-1 |
|
||
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
Стрелки означают, что надо копировать формулы вниз: в столбце А — до строки 8; в столбце В — до строки 9. Результат — в ячейке В9.
Задача З. Шахматная доска
На шахматной доске
64 клетки. На первую клетку кладут 1 зерно, на вторую — 2 зерна, на третью 
З зерна
и т. д.: на каждую следующую клетку кладут на одно зерно больше, чем на
предыдущую.
Сколько всего зерен будет на всей доске и каков вес этих зерен в килограммах, если 15 зерен весят 1 г?
239
Обозначим: i — номер клетки;
S — общее количество зерен. Алгоритм:
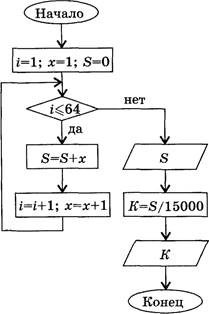
Решение в электронных таблицах:
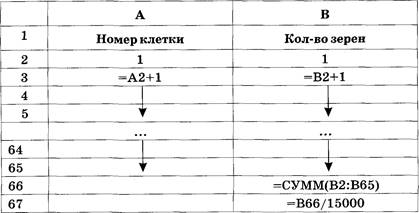
Стрелки означают, что надо копировать формулы вниз до строки 65.
Общее количество зерен записано в ячейке Вбб с помощью формулы =СУММ(В2:В65).
Вес зерен в килограммах записан в ячейке Вб7: =В66/15000.
Задача 4. Кратные числа
Найдите сумму, произведение и количество нечетных чисел от О до 1000, кратных одновременно З и 5.
Решение Обозначим: i — число;
S -— сумма чисел; Р — произведение чисел; К — количество чисел.
Алгоритм:
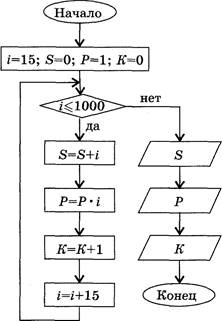
241
в электронных таблицах:
|
|
|
в |
с |
|
||
|
1 |
Число |
Сумма |
Произведение |
Количество |
||
|
2 |
15 |
|
15 |
|
||
|
з |
=А2+15 |
|
|
|
||
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
Стрелки означают, что надо копировать формулу до тех пор, пока число в ячейке столбца А не превысит 1000.
В столбцах
«Сумма» и «Количество» в формулы нужно вместо вопросительных знаков подставить
номер последней ячейки столбца А со значением, меньшим 1000.
В столбце «Произведение» конечное значение будет находиться в строке, номер которой будет известен из столбца А.
Для решения следующих задач также нужно составить алгоритм и выполнить его реализацию в электронных таблицах.
Задача 5. Площадь круга
Выведите таблицу зависимости площади круга от его диаметра, начиная с диаметра, равного 0,1 м, и до тех пор, пока площадь круга не станет больше одного квадратного метра.
Задача 6. Перевод валюты
Один доллар равен 29 рублям. Составьте таблицу перевода рублей в доллары от 2 до 200 рублей с шагом в 5 рублей.
Задача 7. Мешок орехов
Пятеро друзей набрали мешок орехов. В первую ночь первый друг взял 1/5 часть всех орехов. Во вторую ночь второй взял 1/5 часть того, что осталось после того, как свои орехи взял первый. И так далее: каждый следующий брал 1/5 часть того, что осталось. В пятую ночь пятый нашел в мешке 256 орехов.
Сколько орехов набрали мальчики первоначально? Ответ: 625.
Задача 8. В гостях у бабушки
Пятеро подруг гостили у бабушки одной из них. Бабушка набрала девочкам корзину орехов. Пришла первая девочка и досыпала в корзину в З раза больше орехов, чем она там увидела. Пришла вторая девочка и досыпала в З раза больше орехов, чем она увидела в корзине и т. д. Пришла пятая девочка и увидела 2560 орехов. Сколько орехов набрала бабушка? Ответ: 10.
Задача 9. Клетка
В лаборатории в 6 часов утра в колбу положили клетку. Каждые З часа каждая клетка делится на 5 клеток и одна клетка погибает.
Через сколько суток в колбе будет 1 ООО ООО клеток?
Решение
|
1 2 |
|
в с |
||||
|
Сутки
|
|
|
Количество клеток
|
|||
|
|
||||||
|
|
|
|||||
|
||||||
В столбцах А, В, С формулы копируются до тех пор, пока в столбце С не появится число, равное или большее 1 000 000.
Задача 10. Амеба
В лаборатории в 8 часов утра в колбу положили амебу. Каждые 4 часа каждая амеба делится на 4 амебы и 2 амебы погибают.
243
Через сколько суток в колбе будет 1000 амеб?
Решение
|
|
|
в |
с |
|||
|
1 |
Сутки |
Часы |
Количество амеб |
|||
|
2 |
1 |
8 |
1 |
|||
|
|
|
|
|
|
|
|
В столбцах А, В, С формулы копируются до тех пор, пока в столбце С не появится число, равное или большее 1000.
Задача 11. Модель распространения слухов
Один человек в 8 часов утра увидел НЛО. В течение 15 минут он встретил трех своих знакомых и рассказал об этом. В течение следующих 15 минут каждый из этих троих тоже встретил трех своих знакомых и т. д. Продемонстрируйте этот процесс, пока количество людей не станет больше 100 ООО.
Сколько до этого момента пройдет полных часов?
Решение
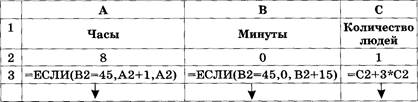
В столбцах А, В, С формулы копируются до тех пор, пока в столбце С не появится число, равное или большее 100 ООО. Количество часов можно прочитать в этой строке в столбце А.
Задача 12. Прогулка в саду
Четыре подруги — Аня, Валя, Саша и Даша — гуляли в саду. Аня нарвала яблок и поделила их поровну между собой и подругами, причем свою часть тут же съела, Затем Валя также поделила яблоки между собой и подругами, а свою часть съела. Затем так же поступила Саша, потом — Даша.
Сколько яблок в итоге осталось у каждой девочки? У кого яблок осталось больше? Решение
|
|
|
в |
с |
|
|
1 |
Аня |
Валя |
Саша |
Даша |
|
2 |
|
|
|
|
|
з 4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
Задача 13. Диофант
Путник! Здесь прах погребен Диофанта, И числа поведать могут,
О чудо, сколь долог был век его жизни.
Часть шестую его представляло прекрасное детство.
Двенадцатая часть протекла 
Покрылся пухом его подбородок.
Седьмую в бездетном браке провел Диофант.
Еще прошло пятилетие 
Он был осчастливлен рожденьем
Прекрасного первенца-сына,
Коему рок половину лишь жизни
Прекрасной и светлой
Дал на земле по сравненью с отцом.
И в печали глубокой
Старец земного удела конец воспринял,
Переживши года четыре с тех пор, как сына лишился. Скажи, сколько лет жизни достигнув, Смерть воспринял Диофант.
Решение
Построим электронную таблицу, задав формулы вычисления продолжительности жизни Диофанта, учитывая, что 9 прошедших лет жизни (5 + 4) без пояснения событий составляют столько частей жизни, какова разность между 1 и суммой всех перечисленных выше частей. Отсюда нетрудно найти, сколько лет составляла вся жизнь Диофанта.
245
|
|
|
в |
|
1 |
детство |
1/6 |
|
2 |
юношество |
1/12 |
|
З |
брак без детей |
1/7 |
|
4 |
еще прошло лет |
5 |
|
5 |
жизнь сына |
1/2 |
|
6 |
после смерти сына |
4 |
|
7 |
сумма всех дробей |
|
|
8 |
сумма лет без пояснения событий |
|
|
9 |
жизнь Диофанта |
|
Ответ: 84 года.
Каждому учителю хочется на уроке настроить учеников на полноценную работу. Предлагаемые задачи учат детей быстро оценивать ситуацию и принимать верное решение. Задачи, решаемые по трафаретам, помогают ученикам максимально сконцентрироваться. Такую учебную работу можно назвать «разминкой для ума».
Учитель читает текст задачи, а ученики решают ее на розданном им готовом трафарете, где делают нужные записи. Для ответа нужно соединить сплошной линией обозначения понятий, между которыми есть соответствие. Проверка проводится фронтально, учащиеся меняются тетрадями и оценивают друг друга. Оценки выставляются по следующему принципу: «5» — без ошибок; «4» — одна ошибка; «З» — две ошибки; «2» — более двух ошибок.
Правильные ответы учитель может продемонстрировать с помощью проектора или написать на доске. Пример трафарета на 5 задач:
1. т
2. с
з. с к в в
4. ю 1
|
п с |
2 з |
|
5. п Р д |
1 2 з |
247
РАБОТА 1
Задача 1
Таня, Оля, Света и Наташа по путевкам поехали во Францию, Италию и Англию. Известно, что только две девочки побывали в одной и той же стране. Оля ездила в Италию. Света была вместе с Наташей не в Англии. Кто из девочек в какой стране побывал?
Решение т
Оф
си
н
Задача 2
Света, Валя и Галя писали сочинение разными чернилами. Одна девочка писала синей ручкой, а две девочки — фиолетовой. Известно, что Света и Галя писали разными чернилами, Галя и Валя тоже. Кто какими чернилами писал сочинение?
Решение
син.фиол.
(1)(2)
Задача З
В Санкт-Петербурге жили три подружки: Соня, Вероника и Ульяна. Их дома были в разных районах: Кировском и Василеостровском. Известно, что Соня и Вероника родные сестры и живут вместе. Соня живет в Кировском районе.
Кто из девочек в каком районе живет?
Решение
в
Задача 4
Юра, Петя и Стас участвовали в соревнованиях по бегу. Петя занял не первое и не второе место. Стас прибежал после Юры.
Какие места заняли мальчики при условии, что они заняли разные места?
Решение ю
1
п2
сз
Задача 5
Володя прочитал за июнь три книги:
«Пятнадцатилетний капитан», «Дети капитана Гранта» и «Робинзон Крузо». Какую
книгу Володя прочитал последней, если известно, что книгу «Пятнадцатилетний
капитан» он прочитал не последней, а книгу «Робинзон Крузо» 
перед книгой
«Пятнадцатилетний капитан» ?
Решение
1
2
д
з
РАБОТА 2
Задача 1
Витя, Саша и Ира делали домашнее задание по математике, русскому языку и литературе. Цвета учебников — синий, красный, белый. Известно, что Витя занимался русским языком по красному учебнику, Саша — литературой не по синему.
Кто какой предмет изучал и какие цвета были у учеб-
ников?
Решение син.мат. кр.РУС. бел.лит.
249
Задача 2
Саша, Витя и Игорь
участвовали в соревнованиях по бегу. Ребята пробежали разные дистанции 
и З
км. Кто-то занял первое место, кто-то второе, а кто-то — третье. Известно, что
Саша бежал не 2 км, но занял первое место. Витя бежал З км и занял не
третье место.
Кто какую дистанцию бежал и какое место занял?
Решение 1
с
1 км
22 км зЗ
км
Задача З
В поле, парнике и саду растут роза, гладиолус и ромашка. Они разных цветов — желтого, красного и белого. Известно, что роза — теплолюбивый цветок и она желтого цвета, гладиолус растет в саду и он не белого цвета.
Узнайте, какого цвета
цветы и где они растут. Решение полежел.
парникбел.
сад
кр.
Задача 4
Юра, Толя, Ира и Катя говорили о собаках. Выясни-
лось, что троим из них нравятся овчарки, а четвертому — бульдоги. У Юры и у Толи разные вкусы. Кате и Юре нравятся разные породы собак. Кому какая порода нравится?
Решение
овчаркабульдог
(3)
10-1703
Задача 5
У Толи, Вовы и Оли есть домашние животные. У кого-то — собака, а у кого-то кошка. Но кошка есть только у одного из ребят. Также известно, что Толя и Вова вместе выгуливают своих любимцев. У кого какое животное?
Решениет
соб.кош.
О
(2)(1)
в
РАБОТА З
Задача 1
Волк, медведь и заяц пошли на день рождения к лисе. Двое купили торт, а один — конфеты. Волк и медведь купили разные подарки, заяц и волк тоже. Кто что подарил имениннице?
Решение в
торт 
конф. м
(2) (1)
з
Задача 2
Три мальчика умеют играть на музыкальных инструментах. Мальчиков зовут Глеб, Вадим и Андрей. Двое из них играют на гитаре, один — на саксофоне.
Кто на каком инструменте играет, если известно, что Глеб играет на духовом инструменте?
Решение
гит.сакс.
(2)
251
Задача З
В зоомагазине четыре девочки покупали птиц. Девочек зовут: Алиса, Ира, Вика и Кира. Две из них покупали попугайчиков, а две — канареек.
Кто какую птицу купил, если известно, что Алиса и Вика не покупали канареек?
Решение
попуг.кан.
(2)(2)
Задача 4
Поход Батыя на Киев, битва со шведами на Неве и Ледовое побоище были в 1240 и 1242 годах. Известно, что два события были в 1240 году, а одно — в 1242 году. Поход на Киев и битва на Неве происходили в один и тот же год.
В каком году каждое
событие произошло? Решение
1242
(1)
Задача 5
Даша, Ксюша и Таня сочиняли стихи и сказки. Две девочки сочиняли стихи, а одна — сказки.
Кто что сочинял, если известно, что Даша и Таня приняли участие в конкурсе с произведениями одного жанра?
Решение
стихисказки
(2)
РАБОТА 4
Задача 1
У Сидорова, Журавлева и Уткина разные профессии — сварщик, журналист и учитель. Первые буквы профессии и фамилии совпадают только у учителя. Кто-то ездит на работу на автобусе, кто-то — на метро, а кто-то — на такси. Журналист не может ездить на метро — ему душно, Журавлев ездит каждый день на такси.
Какие профессии имеют Сидоров, Журавлев и Уткин и на каком виде транспорта они ездят на работу?
Решениеавтобус
сварщик
журналистметро
учительтакси
Задача 2
Оле, Тане и Насте подарили мягкие игрушки: медведя, обезьянку и белку коричневого и рыжего цветов, причем две игрушки — коричневого цвета.
Кому какую игрушку и
какого цвета подарили, если известно, что Оля не любит коричневый цвет,
обезьянка и медведь одного цвета, медведя подарили Тане? Решениемедведь
корич.
(2)
рыж.обезьяна
(1)
белка
Задача З
В саду растут цветы: нарциссы, тюльпаны, купальницы и крокусы. Они белого, желтого, красного и синего цветов.
Определите, какие цветы какого цвета и роста, если известно, что нарцисс — не самый высокий и имеет белуко окраску, тюльпан самый высокий цветок красного цвета, купальницы желтые и они выше крокусов, но ниже нарциссов на 30 см.
Решение
Рассмотрим знаки зодиака: Скорпион, Весы, Дева и Лев. Их планеты-покровители[1] : Солнце, Меркурий, Венера и Марс. Их стихии: вода, воздух, земля и огонь.
Определите, к какому знаку зодиака что относится, если известно, что Скорпион имеет стихию «вода», а его планета Марс, стихия Льва — огонь, и его «планета» самая жаркая. Деве не покровительствует Венера. Деве больше по душе земля, чем воздух.
Решение Солнцевода
Марсвоздух
Венераземля
Мерк.огонь
Задача 5
На день рождения к зайцу пришли Винни-Пух, кот Матроскин и Карлсон. Они подарили зайцу торт, книгу и воздушный шарик.
В каком порядке пришли гости и что каждый из них подарил зайцу, если Винни-Пух и Карлсон не дарили книгу, кот пришел вторым, Карлсон пришел не первым и подарил воздушный шарик?
Решение торт
в
1
книга
м
2 шарик
к
з
РАБОТА 5
Задача 1
Сергей, Эдик и Артем читали книги. Двое читали «Смешные истории», а один — сказки. Эдик и Сережа читали разные книги, Артем и Эдик тоже. Кто что читал?
Решение с
«
Смешныесказки истории»(1)
(2)
Задача 2
Миша, Коля, Вадим и Дима занимаются в разных спортивных секциях: волейбольной, футбольной, лыжной и хоккейной.
Кто чем занимается, если известно, что Миша не любит игровые виды спорта, Вадим никогда не катался на коньках, Дима — лучший волейболист в своей команде?
Решениев
ф
л
д х
Задача З
Русский музей, Казанский собор и Екатерининский дворец построены в Санкт-Петербурге и г. Пушкин. В Санкт-Петербурге находятся два из этих зданий.
Какие здания где находятся, если Екатерининский дворец построен далеко от Казанского собора и Русского музея, а последние — близко друг к другу?
Решение
с.-п.Пушкин
(2)(1)
255
Задача 4
На уроке физкультуры Миша, Сережа, Аня и Толя выполняли упражнения. Трое подтягивались, а один прыгал. Миша и Сережа делали одинаковые упражнения. Миша и Толя тоже. Что делал каждый?
Решение м
подтяг.прыжки
(3)(1)
т
Задача 5
На географии спросили Любу, Машу, Вадика и Юлю о том, какая самая высокая гора в мире. Люба ответила правильно — Эверест. Килиманджаро —- это неправильный ответ. Люба и Вадик ответили по-разному.
Кто как ответил, если трое ответили правильно, а один — неправильно?
Решение
л
ЭверестКилиманджаро
(правильно — З)(неправильно — 1)
РАБОТА 6
Задача 1
Четыре мальчика — Коля, Вася, Толя и Федя — писали контрольную работу. Трое из них написали на «4», и только один написал на «5».
У кого какие оценки, если известно, что Коля и Вася получили разные оценки, а Вася и Толя — одинаковые?
Решение 4
(3)
Саша, Таня, Костя и Дина решили купить йогурты. Трое из них купили малиновые йогурты, а один — банановый.
Кто какой йогурт купил, если известно, что у Дины и Тани йогурты имели разный вкус, а Дина с Костей купили одинаковые йогурты?
Решение малин. с банан.
(3) 
(1)
Задача З
В выходной день
Миша, Володя и Коля решили сходить в музей и в кино. В музей пошли двое, а в
кино 
один.
Кто где побывал в воскресенье, если у Коли с Володей и у Коли с Мишей были разные планы?
|
музей |
кино в |
|
(2) |
(1) |
Решение м
Задача 4
Оля, Таня, Володя, Леша и Сергей нашли разные грибы. У каждого — либо лисички, либо подберезовики, либо белые грузди. Девочки не нашли груздей, а мальчики — лисичек. Оля не нашла подберезовиков. У Оли и Тани разные грибы, у Тани и Володи — одинаковые. У Володи и Леши разные грибы, у Леши и Сергея — одинаковые.
Какие грибы у каждого из них?
Четыре девочки — Катя, Вера, Лена и Оля — ходят в спортивные секции, двое из них на плавание, а двое — на гимнастику.
Кто куда ходит, если известно, что Катя с Леной занимаются в одной секции и у них аллергия на хлорированную воду?
Решение
гимн.плав.
(2)(2)
о РАБОТА 7
Задача 1
Пять девочек — Ира, Даша, Лена, Галя и Таня — рисовали. Три девочки рисовали портреты и две — пейзажи. Известно, что Ира и Даша рисовали разное, Даша с Леной — разное, Лена с Галей — разное. Даша рисовала пейзажи.
Кто что рисовал?
Решение
портретпейзаж
(3)(2)
Задача 2
Четыре мальчика — Юра, Рома, Саша и Миша — выступали на концерте. Три мальчика пели, а один танцевал. Рома с Юрой показывали разные номера, Рома с Сашей — тоже разные. Кто что показывал?
Решение с
песнятанец
(3)(1)
Задача З
 |
Кто какое дерево любит?
Решение
березалипа
(З)(1)
Задача 4
Пять девочек — Света, Таня, Аня, Лена и
Юля 
писали контрольную работу. Три девочки
написали на «пять» и две девочки — на «четыре». Известно, что у Светы с Таней
разные оценки, у Светы с Аней — разные, у Светы с Леной — разные. Кто какую
оценку получил?
Задача 5
Из трех знаков зодиака — Козерог, Стрелец и Рак — два относятся к зимнему времени, а один — к летнему. Если смотреть по лунному календарю, который начинается с весны, то за Раком следует Стрелец, за ним — Козерог.
К какому времени относится каждый знак, если Стрелец приходится на ноябрь—декабрь?
Решение
зималето
(2)(1)
РАБОТА 8
Задача 1
Гиена, газель и коала живут на материках Африка и Австралия. В Африке живут двое из этих животных, а в Австралии — одно. Известно, что гиена нападает на газель.
Где какое животное живет?
Решение
АфрикаАвстралия
(2)(1)
Задача 2
Три города Троян, Брус и Елена относятся к странам Болгария и Сербия. Из них два города относятся к Болгарии, а один — к Сербии. Город Троян находится там же, где и Елена.
В каких странах находятся города?
Решение
БолгарияСербия
(2)(1)
Задача З
Катя, Галя и Даша сажали дубы и тополя. Две девочки сажали дубы, а одна тополя. Галя сажала не дубы .
Кто что сажал?
Решение
 |
(2)(1)
д
Задача 4
Света, Марина и Ксюша ходят в детский сад, там они лепят. Две девочки лепили зайчиков, а одна лисичек. Марина лепила не зайчиков. Кто что лепил?
Решение
зайч.лис.
(2)(1)
Задача 5
Попугаи Кеша, Паша и Тоша умеют говорить. Два попугая говорят «Добрый вечер», а один «Доброе утро» .
Что говорит каждый попугай, если Кеша не говорит «Добрый вечер»?
РАБОТА 9
Задача 1
Из трех видов попугаев — Ара, Жако и Амазон — в Европу завезен один из Африки и два — из Южной Америки.
Какой попугай откуда завезен, если известно, что Ара и Амазон обитают в одной стране?
Решение Ара
АфрикаЮэк. Америка
(1)(2)
Задача 2
Из трех архипелагов 
Канарских,
Гавайских и Мальвинских островов 
два находятся в Атлантическом океане, а
один — в Тихом океане.
Какие острова где находятся, если время на Гавайских островах отличается от времени на Канарских островах на 10 часов, а время на Мальвинских островах отличается от времени на Гавайских островах на 9 часов?
Решение
Атл. океанТихий океан
(2)(1)
м
Задача З
Из трех городов — Мадрид, Бильбао и Глазго — один находится в Великобритании, а два — в Испании. Какой город где находится, если известно, что в Мадриде и Бильбао говорят на одном и том же языке?
На свободном уроке Рита, Даша и Женя делали уроки. Две девочки выполняли задание по математике, а одна — по русскому языку. Даша и Рита выполняли задание по одному и тому же предмету.
Кто чем занимался?
Решение
матем.рус. яз. д
(2) (1)
ж
Задача 5
Четыре мальчика ели
фрукты. Их зовут Сергей, Андрей, Коля и Леня. Трое ели апельсины, а один 
яблоки.
Андрей и Коля ели одинаковые фрукты, а Андрей и Леня — разные.
 |
Решение
ап.ябл.
(3)(1)
РАБОТА 10
Задача [2]
Четыре школы N2N2 5, 10, 13 и 85 — участвовали в соревнованиях. Две школы заняли первое место, а две другие школы поделили второе место. Известно, что школы № 10 и № 5 заняли разные места, № 5 и № 13 тоже. Школа № 5 стала призером . Какая школа какое место заняла?
Олег, Вова, Петя и Митя пошли на день рождения. Один мальчик купил розы, а трое других — гвоздики. Вова и Митя купили разные цветы, Вова и Олег тоже. Кто какие цветы подарил?
Решение о
в
розыгвозд.
(1)(3) п
м
Задача З
Винни-Пух, Кролик и Пятачок взяли на воспитание собак разных пород: немецкую овчарку, болонку и дога, Они дали им разные клички: Пупсик, Мухтар и Рекс.
У кого какая собака и как ее зовут, если Пятачок любит маленьких собачек со смешными кличками, а Винни-Пух назвал Мухтаром пограничную собаку?
Решение бол.Пупсик
нем. овч.Мухтар
дог 
Рекс
Задача 4
Три девочки — Лена, Катя и Валя — учатся в 5, 6 и 7 классах с буквами «А», «Б» и «В».
Кто в каком классе учится и с какой буквой, если Лена учится в 6 классе не с буквой «В», а Катя не в 5 классе с буквой «А»?
Коля, Петя и Миша ходили за грибами: лисичками и подберезовиками. Два мальчика собирали лисички. Миша собирал подберезовики. Кто что собирал?
Решение
лис.подбер.
(2)(1)
РАБОТА 11
Задача 1
Ученики 7А, 7Б и 7В классов посещали по абонементам Русский музей и Эрмитаж. Известно, что Эрмитаж посещали два класса.
|
Решение
ЭрмитажРусский музей
(2)(1)
Задача 2
Вася, Соня, Галя и Юля живут в городах Омск и Тула. Соня, Галя, Юля живут в одном доме. Соня живет не в Туле.
В каких городах живут ребята? Решение в
с
Тула 
Омск
ю
Задача З
Три девочки — Тася, Оля и Алена — собирали черную и красную смородину. Известно, что две девочки из трех собирали черную смородину. Алена и Тася собирали одинаковые ягоды.
Кто какие ягоды собирал?
Решение т
чер. см.красн. см.
(2)(1)
Задача 4
В школе организовали два кружка — антропологии и ботаники. Лена, Оля, Саша и Таня записались в эти кружки. Известно, что две подруги — Лена и Оля — посещают кружок вместе. Саша и Таня не ходят в кружок ботаники.
 |
Решение
антропологияботаника
Задача 5
На темном небе ночью можно увидеть три очень крупные звезды: Бетельгейзе, Ригель и Спику. Звезды находятся в созвездиях Девы и Ориона. Известно, что две из этих звезд находятся в созвездии Ориона, а Спика — самая яркая и большая звезда Девы.
В каком созвездии находится каждая звезда?
Решение
деваОрион
(1)(2)
РАБОТА 12
1
Аня, Ксюша и Олеся — пришли в магазин. Две из них купили платья, а одна —- блузку. Покупки были разных цветов: красного, белого, фиолетового.
Кто купил блузку и какого цвета она была, если Олеся и Ксюша купили одинаковые вещи и их покупки не были красного цвета?
Решение
платьекр.
(2) блузкабел.
(1)
О фиол.
Задача 2
 |
Кто решал задачу с помощью цикла «пока» и какую оценку получил, если известно, что Лена и Ира решали задачи не с помощью цикла «пока» и получили не самые плохие оценки?
Решение З«
пока»
4«для»
5 и «до»
Задача З
У Наташи, Лены и Гали есть игрушки котята, причем разных цветов: желтого, красного, зеленого. Игрушки им подарили их друзья — Илья, Дима, Леша.
У кого желтый котенок и кто его подарил, если известно, что котята Лены и Гали — не желтые, а Илья не дарил котенка Лене и Гале?
Решение ЭКе.Л.
н
Илья кр. л Дима
зел. Леша
Задача 4
Ася, Таня, Алена и Яна пришли в бассейн. Там они плавали брассом, баттерфляем и вольным стилем.
Каким стилем плавала каждая девочка, если Аня и Алена не плавали брассом, но они плавали разным стилем, Алена не плавала вольным стилем, а Яна и Таня не плавали баттерфляем и вольным стилем?
Решение
 |
Задача 5
Закончился учебный
год, началось лето и летние каникулы. Классному руководителю подарили много
букетов цветов. Среди них тремя самыми красивыми были букеты роз, лилий и
орхидей. Эти букеты подарили Лена, Саша и Инна. В каждом букете находилось
разное количество цветков
Известно, что Саша не дарил розы, роз было три, Инна подарила лилии, и их было не пять.
Кто подарил букет орхидей и сколько их там было?
Решение з
розы
5лилии
7орхидеи
РАБОТА 13
1
Катя, Оля и Саша — родились в январе и в апреле. Известно, что две девочки родились в зимнем месяце, а одна — весной.
В каком месяце родилась каждая девочка, если известно, что Катя и Саша родились в разные месяцы, Саша и Оля тоже?
Решение
янв.апр.
(2)(1)
Задача 2
 |
Что исполняли учащиеся этих классов, если в 7 А классе не любили музыку, в 7В классе некоторые занимались бальными танцами?
Решение 
Задача З
В шахматы любит играть один мальчик, в
шашки — двое. Кто во что играет, если Алеша умеет играть в шахматы, а Саша и
Костя свободное время проводят вместе за своей любимой игрой?
Решение
шахм.шаш. (1)(2)
4
Четверо мальчиков — Саша, Олег, Дима и
Андрей 
записались в спортивные секции: трое на
хоккей и один — на футбол.
Кто в какую секцию записался, если Олегу не нравится хоккей?
Решение с
хоккейфутбол
(3)(1)
Задача 5
Три девочки — Оля, Аня и Ира — купили три карандаша — белый и два черных.
Какой карандаш кто купил, если Оля не покупала черного карандаша?
 |
Решение
бел.чер.
(1)(2)
и
РАБОТА 14
Задача 1
Три девочки — Ира, Люба и Настя — собирали цветы. Ира собирала не те цветы, которые собирала Настя. Люба собирала не те цветы, которые собирала Настя. Известно, что две девочки собирали ромашки, а одна — васильки.
Кто какие цветы собирал?
Решение и ром. вас. л
(2) (1)
н
2
Катя, Полина и Лена — шили платья и блузку кукле. Катя и Полина шили разные вещи. Лена помогала Кате. Известно, что Лена шила не платье.
Что шила каждая из девочек?
Решение
платья—П блузки
л
Задача З
Четыре девочки — Вера, Ксюша, Лена и Надя — играли во дворе. Игры назывались «горелки» и «прятки» . Лена играла с Надей, Ксюша не играла в горелки. Вера играла вместе с Ксюшей.
 |
Решение
прят.гор.
(2)(2)
н
Задача 4
Три девочки — Юля, Маша и Даша — для новогодней елки делали игрушки: зайчиков и белочек. Маша и Юля не делали зайчиков.
Кто из девочек какие игрушки делал?
Решение ю
зай. м бел.
д
5
Известны древние богини Рима и Греции: Диана, Флора и Артемида. Они покровительствовали животным и цветам.
Кто кому покровительствовал, если Артемида — греческий аналог Дианы и она покровительствовала животным?
Решение д
жив.
ЦВ.
РАБОТА 15
Задача 1
 |
Кто в каком фильме снимался, если Юрий Никулин снимался только в одном из перечисленных фильмов, а Евгений Леонов не снимался в фильме «Родственные души»? Вместе они не снимались ни в одном из перечисленных фильмов.
Решение
НикулинЛеонов
(1)(3)
Задача 2
Три друга — Костя, Саша и Дима — играли в машинки. Всего было две легковые и одна грузовая машинка. У Саши и у Димы были одинаковые игрушки. У кого какая машинка была?
Решение легк.
д
Задача З
Даша, Света, Оля и Настя поехали кататься на велосипедах. Три велосипеда были марки «Кросс» и один велосипед -— марки «Кама». У Насти и у Светы велосипеды разных марок.
Какие велосипеды у девочек, если известно, что у Светы и Даши одинаковые велосипеды?
Решение «Кросс»«
Кама»
(З)(1)
н
Задача 4
В математической олимпиаде участвовали три мальчика: Петя, Вася и Денис. Перед началом олимпиады было сказано: «Чтобы пройти в следующий тур, надо правильно решить все задания» .
Кто прошел в следующий тур, если Денис не решил одного задания, а остальные решили все задания, но Петя допустил в решении ошибки?
Решение
не прошел 
прошел
д
Задача 5
У четырех девочек —-
Оли, Кати, Алисы и Вики 
есть кошки. Из них три кошки белые, а одна
— черная.
У кого какого цвета кошка, если известно, что у Оли и Кати кошки разного цвета, у Вики и Кати тоже?
Решение о
бел.чер.
(3)(1)
РАБОТА 16
Задача 1
 |
Что рисовал каждый из них?
Решение
м
дер.дом
(2)
(1)
Задача 2
Алла, Вера и Галя вязали. Две девочки вязали шапки, а одна варежки. Алла и Вера вязали разные вещи, Вера и Галя тоже.
Что вязала каждая девочка?
Решение
варежшап. (1)(2)
Задача З
Оля, Света, Юля и Галя собирали марки и открытки. Две девочки собирали марки, две открытки. Света и Галя собирали разное, Оля и Галя тоже. Галя собира-
ла открытки.
Кто что собирал?
Решение С
мар.откр.
(2)(2)
ю
Задача 4
Маша, Даша и Сережа играли на песчаном пляже. Кто-то строил дом, а кто-то делал куличики. Маша не строила дом. Даша работала вместе с Машей, а Сере-
эка —- отдельно.
 |
Решение м
кул. д дом
с
Задача 5
Нина, Валя, Инна, Марина и Костя собирали
фрукты. Трое собирали яблоки, двое — груши. Костя и Марина собирали одинаковые
фрукты, Марина и Валя 
разные, Валя и Нина — разные.
Что собирал каждый из ребят?
Решение
н
в
ябл.гр. и
(3)(2)
м
Задача 6
Люба, Катя, Марина, Даша и Света летом уезжали из города. Две девочки отправлялись в деревню, а три — на юг. Света поехала туда же, куда и Марина. Катя и Марина поехали в разные места, Даша и Марина тоже, Люба и Даша отдыхали вместе.
Кто из девочек поехал в деревню, а кто — на юг?
 |
юг деревня
(3)(2)
с
Литература
1. Богомолова О. Б. Логические задачи по информатике. М.: Информатика и образование, 2001.
2. Болховитинов В. Н., Колтовой Б. И., Лаговский И. К. Твое свободное время. М.: Детская литература, 1975.
З. Брайт В. И. Развиваем интеллект, СПб. , 1997.
4.
 |
5. Духнякова В. Л. Логика, СПб.: Центр развития альтернативного образования, 1996.
6. Задачи для внекласной работы по математике в 5—6 классах / сост. В. Ю. Сафанова. Под ред. Д. Б. Фукса, А. Л. Гавронского. М.: Мирос, 1993.
7. Игнатьев Е. И. В царстве смекалки. М.: Наука, Главная редакция физико-математической литературы, 1978.
8. ЕорДемский Б. А. Математическая смекалка. М.: Государственное издательство технико-теоретической литературы, 1995.
9. Лихтарников Л. А. Занимательные логические задачи. СМ.: Лань, мик, 1996; 1997.
Оглавление
Введение
Раздел 1 . Задачис отношениями
1.1.
Задачи с
транзитивными отношениями
1.2.
 |
Задачи с
некорректными условиями
10
1.3.
Задачи с
отношением равенства
12
1.4.
Задачи с
нетранзитивными отношениями
14
1.5.
Задачи с
несколькими отношениями
. 21
1.6.
Задачи на
сравнение элементов в отношениях
. 26
Раздел 2. Задачи, решаемые с помощью
схем и таблиц
31
Раздел З. Задачи на переправу
. 150
|
Раздел 4. Задачи, решаемые с помощью |
|
|
графов Раздел 5. Задачи на перебор возможных |
|
|
вариантов |
|
|
Раздел 6. Занимательные задачи |
|
|
Раздел 7. Задачи, решаемые по трафаретам |
|
|
Литература |
|
[1] Конечно, каждый школьник знает: Солнце это не планета. Однако астрологические приметы рождались тогда, когда люди еще не знали «устройства» Солнечной системы. — Прим. ред.
[2] Призером считается участник, занявший 2-е или 3-е место. — Прим. ред.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
ник
Линда
Корзина находится вверху
165
