Логика методичка практика 1 часть

логика методичка практика 1 часть

УЧЕБНО-МЕТОДИЧЕСКИЙ МАТЕРИАЛ ПО ИНФОРМАТИКЕ И ИКТ

«АЛГЕБРА ЛОГИКИ»

ПРАКТИКА

1 часть

СОДЕРЖАНИЕ:

1. Основные формы мышления -2

2. Логические операции и порядок составления таблиц истинности

для логических выражений -3

3. Законы алгебры логики. Правила преобразования логических выражений - 5

4.Решение задач с помощью кругов Эйлера - 9

1. Основные формы мышления.

Задание 1.

Какие из приведенных фраз являются высказываниями? Определите значение высказывания (истина или ложь):

1. Обязательно займись спортом.

2. Переводчик обязательно должен знать хотя бы два языка.

3. Ты играешь в футбол?

4. Пять больше трех.

5. Каждый ромб является параллелограммом.

6. В марте 28 дней.

7. Все мальчики – драчуны.

8. Все ученики любят биологию

9. Некоторые ученики любят историю

10. А ты любишь информатику?

11. Посмотри в окно

12. Х*Х*X<0

13. 2*Х -5>0 при X = 3

14. Без труда не выловишь и рыбку из пруда.

15. Как хорошо быть генералом!

16. Революция может быть мирной и немирной.

17. Зрение бывает нормальное, или у человека имеется дальнозоркость или близорукость.

18. Познай самого себя

19. Талант всегда пробьет себе дорогу

20. Москва – столица Эстонии

21. На улице хорошая погода.

22. В город прилетели инопланетяне.

23. Сколько в мире прекрасных людей!

24. Я люблю математику.

25. Кто пойдет в кино?

26. Переведите 1 Кб в биты.

27. В равнобедренном треугольнике углы при основании равны.

28. Число 6 – четное.

29. Париж – столица Китая

30. Посмотрите в окно.

31. Луна – спутник Земли.

32. 4х + 3.

33. Кто отсутствует?

34. 2<3

Задание 2.

Из сложных высказываний выделите простые:

а) Если три стороны одного треугольника соответственно равны трем сторонам другого, то такие треугольники равны.

б) Все ученики изучают математику и литературу.

в) Неверно, что любой четырехугольник – параллелограмм.

г) Завтра будет туман, и мы не сможем вылететь на соревнования.

Задание 3.

Из приведенных простых высказываний и словосочетаний составьте сложные высказывания, используя различные союзы или связки:

1. Поедем на дачу.

2. Хорошая погода.

3. Мы поедем на пляж.

4. Сергей приглашает нас в театр.

5. Сергей приглашает нас в кино.

6. После школы я пойду работать.

7. После школы я поступлю в институт.

8. Сильный ветер.

9. Отсутствие ветра.

10. Плохая погода.

Задание 4.

Постройте таблицы истинности для высказываний:

а) А и (не А) б) А или (не А);

в)не (А влечет В); г) А влечет (не В);

д) А и (А влечет В); е) ( не А) влечет (не А).

Задание 5.

Постройте отрицания высказываний:

а) не (не А); б) не (не (не А));

в) не ( А и В и С ); г) не ( А или В или С ).

Задание 6.

Постройте отрицания высказываний:

а) «Существует собака, у которой одно ухо белое, а другое черное»;

б) « У всех собак плохая память»;

в) «Существует треугольник, у которого сумма углов меньше 180°»;

г) «Каждая задача имеет решение».

2. Логические операции и порядок составления таблиц истинности для логических выражений.

Задание 7.

Таблицы истинности сложных логический выражений.

1.D = ù A \/ ù D /\ ù C ;

2. D = ù ( A \/ B ) /\ ( B \/ C ) ;

3. D = (ù A \/ B ) /\ (ù B \/ C ) ;

4. D = ( B /\ ù A ) \/ ( B /\ ù C ) ;

5. D = ù ( B \/ ù A ) /\ ù ( A \/ C ) ;

6. D = ù (ù B /\ C ) \/ ( A /\ ù B ) ;

7. D = ( B /\ C /\ A ) \/ ù ( A /\ B ) ;

8. D = (ù B \/ ù C ) /\ ù ( A \/ C ) ;

9. D = ( B /\ ù A /\ ù C ) \/ ( B /\ A ) ;

10. D = ( B /\ ù A \/ C ) \/ ù ( A /\ ù C ) .

Задание 8.

Определите, в каком порядке необходимо вычислять значение логического выражения:

Задание 9.

Записать высказывание в форме логического выражения. Определить значение выражения:

• Приставка есть часть слова, и она пишется раздельно со словом.

• Рыбу ловят сачком или крючком, или приманивают мухой или червячком.

• Буква «а» - первая буква в слове «аист» или «сова».

• Я поеду в Таллинн и, если встречу там друзей, то мы интересно проведем время.

Задание 10.

Пусть a = "это утро ясное", а b = "это утро теплое". Выразите следующие формулы на обычном языке:

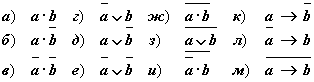
Задание 11.

Составить таблицы истинности следующих выражений:

10.

2. Законы алгебры логики. Правила преобразования логических выражений.

Задание 12.

Упростить выражения:

10.

11.

12.

13.

14.

15.

16.

Задание 13.

Упростите следующие формулы, используя законы склеивания:

· а)

· б)

· в)

· д)

Задание 14.

Упростите следующие формулы, используя законы поглощения:

· а)

· б)

· в)

· г)

Задание 15.

Постройте таблицы истинности для логических формул и упростите формулы, используя законы алгебры логики:

· а)

· б)

· в)

· г)

· д)

· е)

· ж)

· з)

· и)

· к)

Задание 16.

Найдите значения выражение:

а) (1 + 1) Ú (1+0); е) ((1 Ú 0) Ù (1Ù 1) Ù (0 Ú 1);

б) ((1+0)+1) + 1; ж) ((1 Ù А) Ú (В Ù 0)) Ú 1;

в) (А + 1) + (В + 0); з) (( 1 Ù 1) Ú 0) Ù (0 Ú 1);

г) (0 Ù 1) Ù 1; и) ((0 Ù 0) Ú 0) Ù (1 Ú 1);

д) 1 Ù (1 Ù 1 ) Ù 1; к) ((0 × 1)+(1 + 1)) × 1;

Задание 17.

Переведите на язык алгебры логики высказывания

1) « Я поеду в Москву, и если встречу там друзей, то мы интересно проведём время там время».

2) «Если я поеду в Москву и встречу там друзей, то мы интересно проведём там время».

3) «Неверно, что если дует ветер, то солнце только тогда, когда нет дождя».

4) «Если будет солнечная погода, то ребята пойдут в лес, а если будет пасмурно, то пойдут в кино»

5) «Неверно, что если погода будет пасмурная, то дождь тогда и только тогда, когда нет ветра»

6) «Если урок по информатике будет интересным, то ни Миша, ни Света, ни Вика не будут смотреть кино»

Задание 18.

Упростите формулы :

1) A+A×B+A×B×C+A×D×F;

2) A×B+A×B×C+A×B×D;

3) A×(A+B)×(A+C);

4) A×B×(A×C+A×B).

Задание 19.

Символом F обозначена логическая функция от двух аргументов (A и B), заданная таблицей истинности. Какое выражение соответствует F?

1) A → (¬A Ú ¬B) 2) A Ù B 3) ¬A → B 4) ¬A Ù ¬B

Задание 20.

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?

1) ¬(X Ù Y) Ù Z 2) ¬(X Ú ¬Y) Ú Z

3) ¬(X Ù Y) Ú Z 4) (X Ú Y) Ù Z

X	Y	Z	F
0	0	0	1
0	0	1	1
0	1	0	1

Задание 21.

1) A → (¬(A Ù ¬B)) 2) A Ù B

3) ¬A → B 4) ¬A Ù B

A	B	F
0	0	0
0	1	1
1	0	1
1	1	1

Задание 22.

Дан фрагмент таблицы истинности выражения F (см. таблицу). Какое выражение соответствует F?

1) (X ↔ Z) Ù (¬X → Y) 2) (¬X ↔ Z) Ù (¬X → Y)

3) (X ↔ ¬Z) Ù (¬X → Y) 4) (X ↔ Z) Ù ¬(Y → Z)

X	Y	Z	F
1	0	1	0
0	1	0	1
1	1	1	0

Задание 23.

Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?

1) X Ú Y → Z 2) ¬X Ú Y → Z

3) ¬X Ù Z → Y 4) X Ú ¬Z → Y

X	Y	Z	F
1	0	0	1
1	0	1	0
1	1	1	0
0	1	0	1

Задание 24.

Для какого символьного выражения верно высказывание:

¬ (Первая буква согласная) Ù ¬ (Вторая буква гласная)?

1) abcde 2) bcade 3) babas 4) cabab

Задание 25.