Логико-математические игры как условия формирования элементарных математических представлений у детей старшего дошкольного возраста ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА по специальности 44.02.01 Дошкольное образование

МИНИСТЕРСТВО ОБРАЗОВАНИЯ НОВГОРОДСКОЙ ОБЛАСТИ

 

ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ

ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

 «БОРОВИЧСКИЙ ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ»

 

 

 

 

 

Логико-математические игры как условия формирования элементарных математических представлений у детей старшего дошкольного возраста

 

выпускная квалификационная РАБОТА

по специальности 44.02.01 Дошкольное образование

 

Профессиональный модуль

ПМ.03 Организация занятий по основным общеобразовательным программам дошкольного образования

 

 

 

 

 

Работа рекомендована к защите   Рецензент Кириллова Лидия Владимировна Методист ДО2 муниципального автономного учреждения «Средняя общеобразовательная школа №11 с углубленным изучением экономики и биология» г. Боровичи   «     »              2023г. /_________/         Допустить к защите   Нормоконтролёр Архипова Эльвира Николаевна лаборант методического кабинета ОГА ПОУ «Боровичский педагогический колледж» «     »              2023г. /_________/         Заместитель директора (учебная работа) /__________ / С.Г. Поликарпова Приказ от «     »        _2023г. №

Выполнил Федорова Виолетта Сергеевна выпускник 5 курса, очная форма обучения, группа Д1849 Работа завершена «     »              2023г. /_________/         Руководитель Буданова Ирина Владимировна преподаватель ОГА ПОУ «Боровичский педагогический колледж» Работа проверена «     »              2023г. /_________/         Выпускная квалификационная работа защищена «     »              2023г.         Оценка Секретарь ГЭК

 

2023 г.

 

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ	3
1 Теоретические основы формирования математических представлений у детей дошкольного возраста с использованием логико-математических игр	7
1.1 Психолого-педагогические особенности формирования математических представлений у детей старшего дошкольного возраста	7
1.2 Логико-математические игры и их влияния на развитие математических представлений у детей старшего дошкольного возраста	15
2 Применение логико-математических игр в процессе формирования математических представлений у детей старшего дошкольного возраста	27
ЗАКЛЮЧЕНИЕ	51
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ	54
ПРИЛОЖЕНИЕ А	60
ПРИЛОЖЕНИЕ Б	71
ПРИЛОЖЕНИЕ В	73
ПРИЛОЖЕНИЕ Г	100

 

 

 

 

 

 

 

 

ВВЕДЕНИЕ

 

В настоящее время в связи с процессами информатизации и технологиза­ции, происходящими в современном обществе, математическому образованию отводится особая роль, так как математика – весьма значимая область знаний и культурная практика. Двадцать первый век – век информационных технологий, когда наиболее актуальной становится проблема человека мыслящего, творчески думающего, умеющего решать нетрадиционные задачи, основываясь на логике мысли.

Логическое мышление формируется на основе образного и является выс­шей стадией развития мышления. Достижение этой стадии – длительный и слож­ный процесс, так как полноценное развитие логической сферы требует не только высокой активности умственной деятельности, но и обобщенных знаний об об­щих и существенных признаках предметов и явлений действительности, которые закреплены в словах. Начинать развитие логической сферы следует в дошколь­ном детстве.

Требования федерального государственного образовательного стандарта дошкольного образования (далее – ФГОС ДО), представляют собой социально-нормативные характеристики возможных достижений ребенка на этапе заверше­ния уровня дошкольного образования. Ребенок должен проявлять любознатель­ность, задавать вопросы взрослым и сверстникам, интересоваться причинно-следственными связями, пытаться самостоятельно придумывать объяснения яв­лениям природы и поступкам людей, быть способен к принятию собственных решений, опираясь на свои знания и умения.

Развитие всех этих качеств, способствует формированию логической сферы детей дошкольного возраста. Логическое мышление по праву занимает значимое место в системе дошкольного образования. Оно оттачивает ум ребенка, развивает гибкость мышления, учит логике. Взаимозависимость математиче­ского развития и формирования логических приемов умственных действий – одна из основных методических проблем математического образования детей дошкольного возраста, которой уделяли внимание З.А. Михайлова, Л.А. Венгер, А.А. Столяр, А.З. Зак.

В своих работах А.З. Зак подчеркивал, что усложнение и развитие ранней формы мыслительной деятельности ведет к появлению у детей образного мыш­ления, интенсивно развивающегося в период дошкольного детства (Зак, 2005).

Усвоению достаточно сложных логических приемов, понятий, их форми­рованию способствует игра-ведущий вид деятельности детей дошкольного воз­раста. На первый план выходят логико-математические игры и упражнения, как основной вид деятельности детей старшего дошкольного возраста. Логико-мате­матические игры и упражнения направлены на развитие познавательных, иссле­довательских способностей: умению обобщать, сравнивать, выявлять и устанав­ливать закономерности и отношения, решать проблемы, выдвигать их, предви­деть результаты и ход решения задач, обогащать представления о закономерно­стях объектов, об их зависимостях по размеру, количеству, форме, расположе­нию в пространстве.

Проблемой исследования является выявление влияния использования ло­гико-математические игр в работе дошкольных учреждений для формирования элементарных математических представлений у детей старшего дошкольного возраста.

Объект исследования: процесс формирования математических представле­ний у детей старшего дошкольного возраста.

Предмет исследования: применение логико-математические игр в про­цессе формирования математических представлений у детей старшего дошколь­ного возраста.         

Гипотеза: если изучить тeopeтикo-мeтoдичecкиe основы формирования элементарных математических представлений у детей старшего дошкольного возраста, подобрать логико-математические игры и использовать их в совмест­ной деятельности воспитателя и детей старшего дошкольного возраста, то это будет способствовать обучению детей старшего дошкольного возраста матема­тике.

Цель исследования: изучить тeopeтикo-мeтoдичecкиe основы и определить влияние использования логико-математические игр на формирования элемен­тарных математических представлений у детей старшего дошкольного возраста.

Задачи исследования:

–     изучить нормативно-законодательную, психолого-педагогическую и ме­тодическую литературу по проблеме исследования;

–     раскрыть психолого-педагогические особенности формирования мате­матических представлений у старших дошкольников;

–     охарактеризовать понятие и сущность игры, рассмотреть классификации игр для детей дошкольного возраста и описать применение логико-математиче­ских игр в процессе формирования элементарных математических представле­ний у детей старшего дошкольного возраста;

–     выбрать критерии, показатели, подобрать диагностические методики и изучить уровни сформированности математических представлений у детей стар­шего дошкольного возраста;

–     создать развивающую предметно-пространственную среду, насыщен­ную логико-математическими играми для формирования математических пред­ставлений у детей дошкольного возраста математических представлений у детей старшего дошкольного возраста.

Нoвизнa иccлeдoвaния зaключaeтcя в тoм, чтo в paбoте cдeлaнa пoпыткa cиcтeмнo   paccмoтpeть, c тoчки зpeния тeopии и пpaктики, вoпpoc логико-мате­матические игры как условия формирования элементарных математических представлений у детей старшего дошкольного возраста.

Пpaктичecкaя знaчимocть cocтoит в пoдбope yпpaжнeний, игр и cocтaвлeнии кoмплeкcoв логико-математических yпpaжнeний, кoтopыe мoгyт быть иcпoльзoвaны в пpaктичecкoй дeятeльнocти вocпитaтeля гpyппы пpи opгaнизaции paбoты в oбpaзoвaтeльнoй oблacти по математическому paзвитию.

 

1 Теоретические основы формирования математических представлений у детей дошкольного возраста с использованием логико-математических игр

 

1.1 Психолого-педагогические особенности формирования математических представлений у детей старшего дошкольного возраста

 

Формирование математических представлений является одной из самых важных частей интеллектуального и личностного развития дошкольника. В со­ответствии с ФГОС, дошкольное образовательное учреждение является первой образовательной ступенью, выполняя важную функцию подготовки детей к школе. В старшем дошкольном возрасте проблема развития математических представлений наиболее актуальна, что связано с предстоящим переходом ре­бенка к систематическому обучению в школе. Требования ФГОС ДО к образова­тельной программе направлены, в том числе, и на приобретение детьми опыта в игровой деятельности. В дошкольном возрасте ведущим видом деятельности яв­ляется игра. Так как именно в игре ребенок учиться обобщать и делать анализ, запоминать и припоминать то, что нужно в данный момент. Игра является осо­бой, необходимой для гармоничного развития ребенка школой. Это самое при­вычное для дошкольников занятие, в котором дети могут многому научиться.

Традиционными направлениями по формированию математических пред­ставлений являются: 

−    величина – представления о величинах, их измерении и сравнении, (длина, ширина, высота, толщина и так далее); 

−    форма – представления о форме предмета, геометрические фигуры (объ­емные и плоские), их свойства и отношения; 

−    количество и счёт – представления о числе, множестве, счете, арифме­тические действия, задачи; 

−    ориентировка в пространстве – ориентироваться относительно себя, от­носительно другого лица, относительно предметов, а также ориентироваться на листе бумаги, на плоскости; 

−    ориентировка во времени – ориентироваться во временах года, месяцах, днях недели, частях суток, а также развитие «чувства времени» [1, с.17]. 

Основным и ведущим видом деятельности дошкольников является – игра. Рассмотрим подход формирования математических представлений через игро­вую деятельность. Именно развивающие игры осуществляют немаловажную роль в процессе формирования познавательного интереса. Они интересны для детей, эмоционально захватывают их.

Дошкольников повседневно окружают игры, которые способствуют разви­тию, стимулируют познавательный интерес.  Дидактическую игру включают как одно из основных средств реализации программных задач. Дидактические игры по формированию математических представлений условно делятся на следую­щие группы:

–     игры с цифрами и числами;

–     игры путешествие во времени;

–     игры на ориентирование в пространстве;

–     игры с геометрическими фигурами;

–     игры на логическое мышление [2, с.94].

В процессе формирования математических представлений у детей стар­шего дошкольного возраста необходимо учитывать психолого-педагогические особенности этого процесса, чтобы с их учетом выделить условия для успешного формирования этих представлений. Прежде чем рассмотреть эти особенности, раскроем смысл понятий «представления», «математические представления» и «формирование». В психологии «представление – это «чувственный образ явле­ния или предмета, который в данный момент не воспринимается, но был воспри­нят ранее в той или иной форме» [32, с.221]. На основе таких представлений че­ловек может описывать свойства предмета или явления, отсутствующего в насто­ящий момент. У человека нет иного способа общения с внешним миром, чем с помощью уже существующих и вновь создаваемых представлений. В.Д. Шадри­ков уточняет, что представление – это психический процесс, в результате кото­рого образы предметов, явлений и событий возникают в сознании на основе их припоминания или продуктивного воображения» [21, с.31]. Такого же мнения придерживается И.В. Макарова, которая указывает, что «большая часть пред­ставлений – это 22 образы, возникающие на основе ощущений и восприятия. Из данных образов постепенно формируется и корректируется картина мира чело­века» [26, с.73]. Как отмечает Л.С. Выготский, «любое представление, обобщая конкретный предмет (или явление), одновременно может служить обобщением и целого класса аналогичных предметов (явлений). Представления о реальных предметах формируются на основе чувственных восприятий (зрения, слуха, обоняния, осязания). Представления об абстрактных понятиях формируются в деятельности» [15, с.61]. Так, например, представления о геометрических фигу­рах у дошкольников формируются на основе их восприятия (геометрические фи­гуры можно увидеть, потрогать), а представления о величине, количестве фор­мируются у детей в процессе деятельности – порядкового счета, измерения пред­метов. Психологический механизм формирования представлений В.Д. Шадри­ков представляет в виде последовательности процесса познания, в котором ребе­нок от ощущений переходит к восприятию, потом – к формированию представ­лений и затем – к системе знаний об окружающем мире» [21, с.33]. На этой ос­нове в сознании «строятся» чувственнонаглядные образы, которые сохраняются в сознании ребенка благодаря деятельности мышления, памяти, воображения, познавательной активности и речи» [21, с.34]. Итак, в целом представления – это «предшественники» знаний, которые помогают отражать окружающую действи­тельность, существующие в ней связи и отношения. Математические представ­ления являются своеобразным «инструментарием», средствами и способами по­знания, необходимыми для освоения мира и действования в нем: сосчитать ко­личество, определить размер, сравнить, подобрать по размеру и тому подбное. По мнению А.В. Белошистой, «математические представления, логико-матема­тические приемы и способы познания (эталоны, модели, речь, сравнение и дру­гое) составляют первоначальный логико-математический опыт ребенка до­школьного 23 возраста» [5, с.18].

Одним из ведущих познавательных процессов детей дошкольного воз­раста является восприятие, которое «помогает отличить один предмет от дру­гого, объединяет свойства предметов в целостный образ, то есть в форму пред­ставлений, обеспечивает согласованную работу всех остальных познавательных процессов по переработке и получению информации и – в конечном итоге – фор­мирует целостную картину мира в соответствии уровнем развития ребенка» [35, с.183].

Переход от чувственного восприятия формы предмета к ее логическому осознанию осуществляется на базе сенсорного восприятия. Это восприятие у до­школьников, как указывают Н.Н. Поддъяков и В.Н. Аванесовой, «направлено на то, чтобы на основе работы зрительного, слухового, тактильного анализаторов, видеть, узнавать формы предмета наряду с другими его признаками» [36, с.25]. Чтобы лучше познать предмет, дети стремятся коснуться его рукой, взять в руки, повернуть, ощупать. Основную роль в восприятии предмета имеет обследование с последующим обозначением словом. Однако, по наблюдениям Т.В. Тарунтае­вой, «даже у старших дошкольников наблюдается весьма низкий уровень обсле­дования формы предметов: чаще всего они ограничиваются беглым зрительным восприятием и поэтому не различают близкие по сходству фигуры (например, такие как овал и круг, прямоугольник и квадрат, разные треугольники)» [31, с.31].

Формирование математических представлений дошкольников «происхо­дит в сфере интеллектуального развития, особенно – его логического мышления» [32, с.263]. Н.Н. Поддьяков указывает, что «старшие дошкольники уже могут улавливать причинные отношения между наблюдаемыми явлениями, выделять общие схемы причинно-следственных связей и рассуждать о них» [33, с.19]. Про­цесс развития наглядно-образного и словесно-логического видов мышления, по мнению Н.Н. Поддьякова, «связан с овладением ребенком понятиями, то есть знаниями об общих и существенных признаках предметов и явлений действи­тельности, которые закрепляются в словах и терминах» [23, с.69]. В старшем до­школьном возрасте дети могут выделять в предмете те существенные признаки, по которым единичный предмет может быть отнесен к определенной категории или группе, то есть связан с определенным родовидовым понятием» [7, с.47].

Вторая особенность формирования математических представлений у детей дошкольного возраста, по мнению З.А. Михайловой, «состоит в овладении логи­ческими приемами мышления» [39, с.143]. По наблюдениям Е.А. Носовой и    Р.Л. Непомнящей, «в 5-6 лет ребенок может овладеть на элементарном уровне такими приемами логического мышления, как сравнение, обобщение, классифи­кация, систематизация. Формирование этих приемов должно осуществляться с опорой на наглядный материал» [23, с.79]. Е.В. Колесникова считает, что «вла­дение этими приемами ведет к более высокому уровню обобщения предметов и явле­ний, что способствует формированию у детей более полных, осознанных и обоб­щенных математических представлений» [28, с.6].

К логическим приемам мышления относятся анализ, синтез, сравнение, классификация, обобщение, сериация. Их формирование у старших дошкольни­ков имеет свои особенности.

Анализ – «расчленение предмета (мысленное или практическое) на состав­ляющие его элементы с последующим их сравнением и определением суще­ственных и несущественных среди них» [17, с.50].

Синтез – обратный анализу процесс, который «восстанавливает целое, находя существенные связи и отношения, то есть синтез – это построение целого из заданных частей» [17, с.50]. Уже в раннем возрасте (1,5-2 года) в манипуля­тивной деятельности с предметами у ребенка возникают зачатки анализа и син­теза.

Дети 3-4 лет «часто разбирают, точнее ломают игрушки, части которой они потом никак не используют. Это проявление механистического анализа, который оторван от других логических операций мышления» [44, с.290]. По наблюдениям Н.Н. Поддьякова, дети старшего дошкольного возраста способны осуществлять аналитико-синтетическую деятельность, проявляя при этом в ходе анализа: уме­ния выделять части в целом, описать каждую часть, установить связи и отноше­ния между ними, сделать вывод; в ходе синтеза: объединять разрозненные пред­ставления о внешних признаках отдельных предметов и их свойствах в единое целое, перечислить основные части, из которых должно состоять целое, указать их месторасположение, предложить, как соединить эти части в единое целое» [50, с.20].

Сравнение – «логический прием, направленный на установление призна­ков сходства и различия между предметами и явлениями» [17, с.51]. По наблю­дениям Л.Ф. Обуховой, к 5-6 годам ребенок обычно уже умеет сравнивать раз­личные предметы между собой, но делает это, как правило, «на основе только 1-2 признаков, не больше (например, цвета и формы, величины и формы и некото­рых других). Кроме того, выделение этих признаков часто носит случайный ха­рактер и не опирается на разносторонний анализ» [44, с.290].

Классификация – «мысленное распределение предметов на классы в соот­ветствии с наиболее существенными признаками на основе сравнения и обобще­ния» [17, с.53]. Обобщение – «мысленное объединение предметов и явлений по их общим и существенным признакам» [17, с.51]. Старшие дошкольники спо­собны к простым обобщениям: «Лошадь – это животное, зверь», «Карандаш – палочка для рисования, писания», «Кукла – игрушка», «Вилка – это посуда» и так далее. Однако, встречая малознакомые предметы, ребенок опускается на уро­вень беспорядочного перечисления их внешних признаков или указывает на назначение предмета: «Барометр – это такой круглый, и стрелка, как часы, чтобы погоду узнавать» [33, с.70]. Овладеть приемами обобщения и классификации в полном объеме старшие дошкольники пока не в состоянии» [34, с.291].

Сериация – «упорядочивание объектов по степени интенсивности одного или нескольких признаков» [17, с.54]. В.В. Данилова, Т.Д. Рихерман и З.А. Ми­хайлова считают, что в старшем дошкольном возрасте ребенок может овладеть следующими умениями, необходимыми для осуществления систематизации и сериации: «находить закономерность расположения объектов, упорядоченных по одному признаку и размещенных в одном ряду; упорядочивать объекты ряда, расположенные случайным образом; находить закономерность расположения объектов, упорядоченных на основе двух и более признаков» [19, с.61].

Однако в целом не следует переоценивать умственные возможности детей старшего дошкольного возраста. Словесно-логическая форма мышления хотя и доступна, но еще не характерна для них. Даже приобретая черты обобщенности, их мышление остается в основном наглядно-образным, опирающимся на реаль­ные действия с предметами и их «заместителями».

По наблюдениям Л.Ф. Обуховой, в возрасте пяти лет «внимание ребенка еще неустойчиво, он не может сам долго сосредоточиваться на чем-либо, делает это только под влиянием взрослого, когда, например, воспитатель говорит: «Будь внимательным», «Слушай внимательно», «Смотри внимательно» [34, с.104]. Вы­полнение требований взрослого способствует развитию произвольного внима­ния ребенка.

Старший дошкольный возраст характеризуется интенсивным развитием способности к запоминанию и воспроизведению. Память ребенка этого возраста еще «носит непроизвольный характер» [37, с.156]. Это значит, что ребенок чаще всего не ставит перед собой осознанных целей что либо запомнить, и запомина­ние и припоминание происходит независимо от его воли и сознания: «ребенок запоминает то, на что было обращено внимание в деятельности, что произвело на него впечатление, что было интересно» [37, с.157]. Наиболее благоприятные условия для овладения произвольным запоминанием и воспроизведением созда­ются в игре.

При развитии математической речи детей воспитатель добивается, чтобы ребенок понимал, о чем идет речь, и сам мог грамотно сформулировать свои наблюдения, умозаключения, выводы и обобщения. По словам А.В. Белошистой, «такого рода исследовательско-лингвистическая работа увлекает дошкольников и способствует тому, что сложные математические термины осознаются, а не за­поминаются путем зубрежки» [9, с.47].

Н.А. Арапова-Пискарева полагает, что «главная роль в формировании ма­тематических представлений у дошкольников принадлежит обучению» [3, с.16]. Следовательно, важно создать педагогические условия для успешного формиро­вания математических представлений у детей дошкольного возраста. Эти усло­вия относятся к сфере образовательной деятельности. На третью особенность и связанное с ней педагогическое условие указывал А.В. Запорожец, который пи­сал, что важными элементами системы формирования математических представ­лений у дошкольников являются «задачи и содержание обучения» [22, с.319].

В содержании формирования математических представлений детей 5-          6 лет, согласно программе «От рождения до школы», входят представления о мно­жестве и подмножестве, прямой и обратный счет с помощью различных ана­ли­заторов (зрительного, слухового, тактильного), счет групп предметов, деление целого на части, сопоставление совокупности предметов, независимость числа предметов от их размера и формы расположения, решение текстовых арифмети­ческих задач и так далее [45, с.56].

В образовательной программе «Детство» сформулированы следующие за­дачи по формированию элементарных математических представлений у детей подготовительной к школе группы: сравнивать объекты по заданному признаку; классифицировать картинки и строить наглядную модель понятийных отноше­ний; изготавливать заместители в соответствии с выраженностью признака, ве­личины объекта; определять соотношение понятий по выраженности признака на основе созданной модели; группировать объекты по заданному признаку и соотносить полученные группы с наглядной моделью.

В этой программе определено содержание математического образования дошкольников по разделам «Свойства», «Отношения», «Числа и цифры», «Со­хранение (неизменность) количества и величины», «Алгоритмы», названы виды деятельности детей: доматематические (сравнение, уравнивание, комплектова­ние, элементы логики и математики) и математические (счет, измерение, вычис­ление).

В программе «Детство» перечислены методы формирования математиче­ских представлений у старших дошкольников:

−    практические (игровые);

−    экспериментирование;

−    конструирование и моделирование;

−    воссоздание;

−    преобразование;

Таким образом, анализ литературы показал, что к психолого-педагогиче­ским особенностям формирования математических представлений у старших до­школьников относятся:

–     сенсорная основа формирования этих представлений (от восприятия к мысленному образу, а затем – к понятиям), достаточный уровень развития вос­приятия, наглядно-образного мышления, внимания, памяти, воображения и речи детей;

–     овладение логическими приемами мышления;

–     выполнение программных задач и программного содержания по форми­рованию элементарных математических представлений у детей определенного возраста.

Учет этих особенностей позволил выделить следующие условия, которые необходимо создать для успешного формирования элементарных математиче­ских представлений у старших дошкольников:

–     разработка и внедрение комплекса логико-математических игр;

–     подбор логико-математических игр с учетом возрастных особенностей, возможностей и интересов детей старшего дошкольного возраста;

–     выполнение программных требований по задачам и содержанию форми­рования элементарных математических представлений у детей старшего до­школьного возраста – количественных, числовых, геометрических, простран­ственных, временных представлений и представлений о величинах;

–     развивающая предметно-пространственная среда, эффективная для фор­мирования элементарных математических представлений у старших дошкольни­ков.

Таким образом, развивающие игры как средство формирования математи­ческих представлений для детей старшего дошкольного возраста, являются неотъемлемой частью учебной деятельности. Они способствуют развитию ин­теллектуальных, творческих и математических способностей ребенка, а также являются средством воспитания, как для ребенка, так и для взрослого. Большое внимание уделяют формированию произвольного внимания и памяти, развитию умственных действий (анализ, синтез, сравнение, обобщение), смекалки и сооб­разительности, развитию интереса к приобретению знаний, которое постигается через игру.

 

1.2 Логико-математические игры и их влияния на развитие математических представлений

 

Логико-математические игры развивают у детей: самостоятельность, спо­собность автономно, независимо от взрослых решать доступные задачи в разных видах деятельности, а также способность к элементарной творческой и познава­тельной активности. Способствуют: освоению детьми средств познания: этало­нов (цвет, форма, эталонов мер (размер, масса, моделей образов, представлений речи; накоплению логико-математического опыта, овладению способа­ми позна­ния: сравнением, обследованием, уравниванием, счетом.

Для данного вида игр характерна: игровая направленность деятельности, насыщение проблемными ситуациями, творческими задачами, наличие ситуаций поиска с элементами экспериментирования, практического исследования, схема­тизацией. Обязательным требованием к данным играм является их развивающее воздействие.

Логико-математические игры конструируются на основе современного взгляда на развитие математических способностей ребенка. К ним относятся стремление ребенка получить результат: собрать, соединить, измерить, проявить инициативу, и творчество; предвидеть результат; изменить ситуацию; активно не отвлекаясь, действовать практически и мысленно; оперировать образами; устанавливать связи и зависимости, фиксировать их графически.

Данные игры способствуют развитию внимания, памяти, речи, воображе­ния и мышления ребенка, создают положительную эмоциональную атмосферу, побуждают детей к обучению, коллективному поиску, активности в преобразо­вании игровой ситуации.

Современные логико-математические игры разнообразны: настольно-пе­чатные игры: «Цвет и форма», «Игровой квадрат», «Геометрический конструк­тор»; игры на плоскостное моделирование: «Танграм»; игры из серии «Кубики и цвет»: «Сложи узор», «Сложи квадрат».

 В ходе логико-математических игр ребенок осознанно воспринимает иг­ровую задачу, целенаправленно решает ее.

Также в работе с детьми, использую большое количество коллективных игр, как в совместной, так и в самостоятельной деятельности. Это такие игры, как «Геометрическое лото», «Домино», «Угадай-ка», «Найди пару», «Засели до­мики», «Сложи гусеницу», «Найди лишнее», «Собери бусы», «Подбери за­платку», «Сложи квадрат», и так далее.

Все логико-математические игры учат детей мыслить логически, удержи­вать в уме сразу несколько свойств предмета, уметь кодировать и декодировать информацию.

Использование развивающих, логико-математических игр способствует появлению у ребят интереса к познавательной деятельности, развитию их мыш­ления, речи, воображения, мелкой моторики рук. Каждый ребенок учился играть в своем темпе, так как после занятий можно было еще раз выполнить задание, лучше понять его суть.

Немаловажную роль занимает организация самостоятельной деятельности в специально организованной развивающей среде. В свободном пользовании у детей находятся разнообразные логико-математические игры: «Сделай сам», «Сложи квадрат», «Игровой квадрат», «Танграм», «Сложи узор», «Игра с цве­том», «Змейка», «Собери бусы», «Гусеница» и другие.

В основных образовательных программах дошкольного образования со­держание работы по формированию логико-математических представлений представлено как:

–     развитие представлений:

а)   о математических свойствах и отношениях предметов;

б)  числах;

в)  величинах;

г)   геометрических фигурах;

д)  зависимостях и закономерностях;

–     освоение экспериментально-исследовательских способов познания ло­гико-математического содержания:

а)   моделирование;

б)  экспериментирование;

в)  трансформация;

–     развитие сенсорных (предметно-действенных) способов познания ло­гико-математических свойств и отношений:

а)   обследование;

б)  упорядочивание;

в)  группировка;

г)   разбиение;

д)  сопоставление;

–     развитие логических способов познания:

а)   анализ, сравнение;

б)  обобщение, классификация;

в)  сериация, абстрагирование, отрицание;

–     овладение логико-математическими способами познания:

а)   счет, измерение, простейшие;

б)  вычисления.

В своем исследовании З.А. Михайлова и Е.А. Носова выделили логико-математические представления и способы их познания, которые лежат в основе построения работы по формированию логико-математических представлений у детей дошкольного возраста (приложение В).

Развитие логического мышления и познавательной активности невоз­можно без участия родителей. На всех этапах требуется поддержка ребенка дома, в семье. Развитие познавательной активности происходит исходя из потребности в получении новых знаний, которая присуща большинству людей от рождения. В старшем дошкольном возрасте на основе потребности в получении новых зна­ний, в процессе формирования ориентировочной, исследовательской деятельно­сти, у детей формируется стремление открыть и узнать для себя больше нового.

Анализируя образовательные программы по формированию математиче­ским представлениям можно отметить, что дети старшего дошкольного возраста осваивают способы установления различного рода математических отношений, связей, самостоятельности мышления, а также мыслительных операций сравне­ния, анализа, синтеза, способности к отвлечению и обобщению, к пространствен­ному воображению.

Таким образом, включение логико-математических игр в образовательном процессе в развитии познавательной активности детей дошкольного возраста со­держит в себе большие потенциальные возможности: активизирует познаватель­ные процессы (мышление, внимание, память, воображение), формирует любо­знательность, позволяет ребенку проявлять самому инициативу; закрепляет зна­ния, умения, навыки. Логико-математические игры представляют собой игры, моделирующие математические закономерности, отношения, предполагающие выполнение доступных для ребенка логических действий и операций. В процессе игры дети осваивают операции мышления. Логико-математические игры – «раз­новидность математических игр, которые специально разрабатываются таким образом, чтобы они формировали не только элементарные математические пред­ставления, но и логические приемы мышления, необходимые для формирования у дошкольников элементарных математических представлений» [34, с.186].

Этим объясняется название «логико-математические игры». Отличитель­ными особенностями этих игр являются: творческие задачи, проблемные ситуа­ции, ситуации поиска с элементами экспериментирования, практического иссле­дования, схематизации, моделирования и конструирования.

А.В. Белошистая отмечает, что логико-математические игры конструиру­ются на основе современного взгляда на развитие математических способностей ребенка-дошкольника: «стремление получить практический результат: собрать, соединить, измерить, отсчитать нужное количество, построить, сконструиро­вать; проявить самостоятельность, инициативу и творчество; изменить ситуа­цию; действовать практически и мысленно; оперировать образами; устанавли­вать связи и зависимости, фиксировать их графически, делать выводы и обобще­ния» [6, с.249].

В настоящее время в процессе формирования математических представле­ний у дошкольников реализуется идея логической подготовки дошкольников А.А. Столяра, которым разработана методика введения детей в мир математиче­ских представлений посредством обучающих логико- математических игр.     А.А. Столяр отмечает, что эти игры «выполняют свою обучающую функцию го­раздо успешнее, если они применяются целенаправленно и в системе, предпола­гающей вариативность, постепенное усложнение и по содержанию, и по струк­туре, связь с другими методами и формами работы по формированию элементар­ных мате­матических представлений» [30, с.106].

Система обучающих игр А.А. Столяра состоит из отдельных серий. Каж­дая серия игр предназначена для формирования отдельных логических приемов мышления или подготовки к усвоению определенного математического понятия или математической закономерности. Внутри каждой серии игры располагаются в определенной последовательности с постепенным усложнением игровых за­дач, стоящих перед детьми. Наряду с развивающей функцией эти игры выпол­няют обучающую функцию. Например, изображая работу «вычислительной ма­шины» (в виде блок-схемы или программы машины Поста), дети обучаются вы­полнять арифметические действия над числами. Некоторые из этих игр являются сюжетно-отобразительными играми с правилами. Например, игра «Кто где жи­вет?» имеет дидактическую задачу: сформировать представления о внутренней и внешней области по отношению к замкнутой линии, включить в активную речь детей словосочетания «внутри обруча» и «вне обруча» [29, с.33]. Игровые дей­ствия в ней носят соревновательный характер (кто быстрее выполнить опреде­ленные правилами действия).

Современные логико-математические игры очень разнообразны по своему виду и задачам. Это разнообразие делает их наиболее эффективными для форми­рования у детей количественных, пространственных, временных представлений, представлений и величие, форме, и цвете. Кратко охарактеризуем эти игры.

Настольно-печатные игры – это «игры, в которые дети играют за столом, в них используются разрезные картинки, карточки (например, «Цвет и форма», «Игровой квадрат», «Логоформочки» и другие)» [11, с.133]. По задачам эти игры могут быть на выделение части и целого; на развитие приемов логического мыш­ления: обобщение, сравнение, счет, составление задач, ассоциации, классифика­цию, сериацию; на формирование умения ориентироваться в пространстве; на усвоение математических знаков и символов.

Особую группу логико-математических игр составляют игры на конструи­рование и моделирование, в которых детям предлагается выполнить математи­ческие задания из объемных или плоских фигур. Например, игры на объемное моделирование («Кубики для всех», «Геометрический конструктор», «Шар»); игры-головоломки по конструированию на плоскости («Волшебный круг», «Ко­лумбово яйцо»); игры на плоскостное конструирование и моделирование (ста­ринная восточная головоломка «Танграм», «Крестики», «Соты», «Монгольская игра», «Вьетнамская игра», «Пентамино» и так далее) [43, с.23]. Очень увлекают детей 5-7 лет математические игры-развлечения (головоломки, ребусы, лаби­ринты, математические загадки, задачи-шутки, кроссворды (словесные по мате­матическому материалу и числовые), магические квадраты).

А.В. Белошистая утверждает, что математические игры-развлечения «ин­тересны по содержанию, занимательны по форме, отличаются необычностью ре­шения, парадоксальностью результата» [5, с.261].

Головоломка – это задача, для решения которой, как правило, требуется сообразительность и смекалка, и математические знания. Например, в голово­ломке «Веселые пингвины» от ребенка требуется расставить 7 пингвинов таким образом, чтобы сумма чисел, проставленных на пингвинах во всех указанных ря­дах, составляла 12.

Математический ребус – «особый вид загадок, в которых загаданные слова зашифрованы с помощью последовательности картинок, букв, цифр и других символов» [5, с.262]. При решении этих ребусов дети получают ответы матема­тического характера – это математические термины: например, «минус», «вычи­тание», «сложение», «задача», «два» и так далее.

Лабиринт – «запутанные дорожки (линии), часть из которых оканчивается тупиком или неправильным ответом, и только один путь – правильный, он пред­ставляет собой выход из лабиринта» [5, с.262]. Его и должен найти ребенок.

К словесным логико-математическим играм относятся старинные матема­тические задачи, задачи на смекалку и задачи-шутки. Их применение, по мнению Е.И. Щербаковой, обеспечивает «развитие умений считать, оперировать циф­рами, количественными величинами и отношениями, умениями сравнивать, обобщать, классифицировать» [34, с.344]. Старинные задачи интересны для до­школьников тем, что из них дети узнают, что было важно сосчитать для наших предков, какими предметами быта они пользовались, чем занимались. Логиче­ские задачи на смекалку в своих условиях содержат намеки и подсказки на пра­вильное решение. Они способствуют развитию «критичности мышления, при­учают к анализу воспринимаемой информации, ее разносторонней оценке, повы­шают интерес к математике» [34, с.345].

Задачи-шутки – это занимательные игровые задачи с математическим смыс­лом. Для решения таких задач надо проявить находчивость, смекалку, по­нима­ние юмора.

Математические загадки – это рифмованные строки, небольшие стихотво­рения, их отгадки – математические термины и понятия: цифры (от 0 до 9), ма­тематические знаки (плюс, минус, равно) и так далее. К этому же виду логико-математических игр относятся загадки-шутки, взятые из литературных произве­дений. Например, очень известная загадка-шутка про Кондрата, который «шел в Ленинград», составленная К. Чуковским, в которой нужно правильно определить направление движения, а не производить довольно сложные математические вы­числения, чтобы ответить на вопрос: «Сколько мышат и котят ребята несут в Ле­нинград?».

Среди логико-математических игр есть и подвижные игры, которые, фор­мируют математические представления дошкольников в двигательной активно­сти. Например, игра «Больше – меньше» направлена на «формирование логиче­ского приема сравнивать предметы по размеру и одновременно – на развитие моторной координации движений» [38, с.115].

Варианты этой подвижной игры – формирование понятий «выше – ниже», «толще – тоньше», «длиннее – короче» и другие. Подвижная игра «Покажи по­разному» построена по тому же принципу: дети по словесному сигналу (воспи­татель произносит словосочетания), меняют характер своих движений [58, с.117]. Например, воспитатель говорит «высокие ворота», и дети шагают в пол­ный рост, потом воспитатель говорит «низкие ворота», дети выполняют ходьбу в полуприсяде и так далее.

К конструктивным логико-математическим играм, которые применяются для формирования элементарных математических представлений у старших до­школьников, относятся логические блоки Дьенеша и палочки Кюизенера.

В нашей стране, как и во многих странах мира, успешно используются ло­гико-математические игры с блоками З.П. Дьенеша, разработанные венгерским психологом и математиком Дьенешем. Блоки Дьенеша – универсальный дидак­тический материал, представляющий собой набор из 48 объемных геометриче­ских фигур (круги, треугольники, квадраты, прямоугольники), раскрашенные в красный, синий и желтый цвет, большие и маленькие по размеру, разные по тол­щине. Основная цель использования блоков Дьенеша: научить решать логиче­ские задачи на разбиение по свойствам.

Основные умения, необходимые для решения логико-математических за­дач – это «умения выявлять в объектах разнообразные свойства, называть их, адекватно обозначать словом их наличие или отсутствие, абстрагироваться и удерживать в памяти одно или одновременно два или три свойства объектов, обобщать объекты по одному, двум или трем свойствам с учетом наличия или отсутствия каждого» [25,с.35]. Именно эти умения формируются у дошкольников с помощью логических блоков Дьенеша, которые могут быть широко использо­ваны воспитателем в формировании элементарных математических представле­ний детей как в организованной взрослым деятельности, так и в самостоятельной деятельности детей.

Методика применения логико-математических игр с помощью блоков Дье­неша состоит в постепенном переходе от простых игр к более сложным по своим правилам. Например, вначале ребенку дается задание отобрать одинаковые по только размеру и форме фигуры и построить из них то, что захочет ребенок. За­тем проводятся игры, более сложные по своим правилам. Игры с блоками Дье­неша могут включать смежные правила, но отличаться игровым материалом для решения поставленной игровой задачи. Палочки Кюизенера названы по фамилии бельгийского педагога, который первым предложил использовать цветные бру­сочки для формирования математических представлений детей. При разработке своей методики он опирался на идеи М. Монтессори и Ф. Фребеля. Это дидакти­ческий набор, в который входят 116 палочек (самый простой вариант) или 241 палочка (классический вариант), окрашенные в 10 различных цветов и имеющие размер от 1 см до 10 см [21,с.50]. К набору прилагаются карточки-схемы, по которым организуются игры.

Логико-математические игры с палочками Кюизенера формируют пред­ставления о размере, цвете, длине, количестве и счете, о соотношении цифры и числа, ориентировке в пространстве (верх – низ, слева – справа, спереди – сзади и так далее).

Разработанный М. Монтессори сенсорный материал используется в ло­гико-математических играх на обучение дошкольников умениям различать и классифицировать признаки предметов, различать геометрические фигуры, срав­нивать числа. В сенсорном материале Монтессори представлены самые разные воспринимаемые качества объектов – форма, цвет, размеры, температура, вес, гладкость или шероховатость поверхности, запахи, звуки и другое, причем дан­ные качества как бы «очищены», «изолированы» от самих предметов [38, с.46]. Так, например, для различения высоты или объема используются просто цилин­дры или призмы, убывающие в размерах; для различения формы – плоские гео­метрические фигуры; для различения цвета – простые таблички из цветной бу­маги или цветного шелка. Специальной задачей многих игр является «сериация, то есть расположение предметов в порядке убывания (или возрастания) качества: от бледного к самому интенсивному оттенку цвета, от самой гладкой к самой шероховатой поверхности, от самого широкого к самому узкому кубику и так далее» [68, с.51].

Для формирования математических представлений у старших дошкольни­ков применяется игровая технология – круги Эйлера. Это геометрическая схема, с помощью которой наглядно отображаются отношения между множествами объектов или понятий. Игры с кругами Эйлера формируют у старших дошколь­ников приемы логического мышления: анализ, синтез, обобщение; установление причинноследственных связей; выбор оснований для сравнения, классификации объектов; подведение под понятие, выведение следствий; построение логиче­ской цепи рассуждения, формулирование вывода [25,стр.24]. В играх с кругами Эйлера используются пересекающиеся, непересекающиеся, равные между собой множе­ства и множества, состоящие из подмножеств. С ними проводятся игры на фор­мирование количественных представлений у детей, понимания состава чисел, представлений о форме, цвете и размере геометрических фигур, умений сравни­вать и классифицировать. Большую группу составляют логико-математические игры на формирование пространственных и временных представлений и у стар­ших дошкольников.

Логико-математические игры на формирование пространственных пред­ставлений у старших дошкольников – это игры-лабиринты, игры, в которых иг­ровое задание учит ребенка ориентироваться на листе бумаги, в пространстве ка­кого-либо помещения, по схемам и картам. Например, игра «найди игрушку», в которой по устной инструкции воспитателя, в какую сторону нужно двигаться, ребенок находит игрушку и после этого повторяет свой маршрут. Или игры на формирование умения ориентироваться на листе бумаги, которые проводятся по типу «графического диктанта». Воспитатель указывает направление «в центре», «посередине», «справа», «слева», «левый (правый) верхний угол», «левый (пра­вый) нижний угол», а дети отображают его карандашом на листе бумаги. Это игры «Фигуры высшего пилотажа» (или «Летчики»), «Я еду на машине (на вело­сипеде)», «Путешествие на корабле», «Футбол», «Космос» и другие. В игре «До­рога в детский сад» ребенок по схеме должен рассказать, какие объекты он про­ходит, когда идет в детский сад. Эти игры подробно описаны в методических пособиях А.В. Белошистой, З.А. Михайловой, Т.А. Мусейибовой и других.

Логико-математические игры на формирование временных представлений у детей старшего дошкольного возраста по содержанию – это игры на:

–     знание названий частей суток, дней недели, их последовательности, ме­сяцев, времен года, их последовательности и того, какие месяцы составляют то или иное время года;

–     умения определять: какой день был вчера, сегодня, будет завтра; время с использованием календаря и часов; время по цикличности природных явлений и деятельности человека в то или иное время суток или времени года [54, с.89]. По видам они очень разнообразны: настольно-печатные («Сутки», «Части суток» (работа по картинкам), «Веселый поезд» (понятия «вчера», «сегодня», «завтра»),

Н.В. Нищева предлагает проводить усвоение разнообразной деятельности человека, характерной для каждой из частей суток, посредством игр [45, стр.23]. Это могут быть игры-путешествия в утро, день, вечер и ночь. В ходе таких игр дети закрепляют навык в определении частей суток, свободного включения в речь их названий.

Таким образом, логико-математические игры широко и активно применя­ются в процессе формирования элементарных математических представлений у детей старшего дошкольного возраста. Они отличаются большим многообра­зием: наглядно-печатные, словесные, конструкторские (с плоскими и объем­ными фигурами), подвижные. На основе указанных особенностей этих игр можно сформулировать следующие рекомендации по их применению в процессе формирования элементарных математических представлений у детей старшего дошкольного возраста:

–     каждая игра должна содержать элемент новизны, формировать новые для детей математические представления, умения и навыки;

–     воспитателю необходимо не только уметь проводить игру, но и увле­ченно играть вместе с детьми;

–     ни в коем случае нельзя применять дисциплинарные меры к детям, нару­шившим правила игры или игровую атмосферу.

 Это может быть лишь поводом для доброжелательного разговора, объяс­нения, а еще лучше, когда, собравшись вместе, дети анализируют, разбирают, кто как проявил себя в игре и как надо была бы избежать конфликта.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 Применение логико-математических игр в процессе формирования математических представлений у детей старшего дошкольного возраста

 

Практико-ориентированное исследование осуществлялось на базе муници­пального автономного дошкольного образовательного учреждения детский сад «Березка» города Боровичи. В практико-ориентированное исследование прини­мали участие 20 детей старшей группы, в возрасте 5-6 лет. Все эти дети посе­щают детский сад в течение трех-четырех лет.

Цель практико-ориентированного исследования – обоснование эффектив­ности использования логических игр в качестве условия формирования элемен­тарных математических представлений у детей старшего дошкольного возраста.

Задачи:

–     определить уровень знаний детей старшего дошкольного возраста;

–     выбрать критерии, показатели, подобрать методики, направленные на выявление уровня сформированности математических представлений у детей старшего дошкольного возраста;

–     провести диагностическое изучения уровней сформированности мате­матических представлений у детей старшего дошкольного возраста, обработать результаты, представить их графически, сделать выводы.

 Опытно-поисковая работа состояла из трех этапов:

–     первый этап – констатирующий. Первичное изучение уровня сформиро­ванности математических представлений у детей старшего дошкольного воз­раста;

–     второй этап – формирующий. Проведение работы по формированию ма­тематических представлений у детей старшего дошкольного возраста с исполь­зованием логико-математических игр. Цель этапа заключалась в создании педа­гогических условий для успешного формирования элементарных математиче­ских представлений у старших дошкольников, главным из которых является раз­работка и реализация комплекса логико-математических игр, обеспечивающих формирование этих представлений;

–     третий этап – контрольный. Итоговая диагностика уровней сформиро­ванности математических представлений у детей и проведение сравнительного анализа результатов обследования до и после использования комплекса логико-математических игр.

На первом этапе была определена база исследования детей старшего до­школьного возраста, которые подлежат обследованию. Затем была разработана программа диагностического изучения уровней сформированности математиче­ских представлений у детей старшего дошкольного возраста, определены крите­рии, показатели, уровневые характеристики сформированности математических представлений у детей, подобраны методики, стимульный материал и инструк­ции к ним для изучения математических представлений детей. Далее было про­ведено первоначальное обследование детей, составлен сводный протокол. Полу­ченный экспериментальный материал был обработан с применением методов ко­личественного и качественного анализа, проведена интерпретация полученного материала, сделаны выводы по результатам первого этапа опытно-поисковой ра­боты.

Целью первого этапа стало изучение начального уровня сформированно­сти математических представлений у детей старшего дошкольного возраста.

Задачи этапа:

–     подобрать методики и диагностические задания (критерии, показатели, уровневые характеристики) для оценки уровня сформированности математиче­ских представлений у детей старшего дошкольного возраста;

–     провести диагностическое изучение начального уровня сформированно­сти математических представлений у испытуемых детей, проанализировать его результаты, сделать выводы;

–     дать качественный и количественный анализ уровням и особенностям математических представлений детей старшего дошкольного возраста.

На основе анализа психолого-педагогической литературы были опреде­лены критерии и показатели сформированности математических представлений у старших дошкольников, предложенные в программе «От рождения до школы» [46, с.45] (таблица 1).

Таблица 1 – Критерии и показатели сформированности элементарных математических представлений у детей 5-6 лет

 

Критерии	Показатели
1 Количественные представления и счет	– соотнесение числа с количеством в пределах 8; – порядковый счет от 1 до 10;  – умение оценивать количественную характеристику видоизменяющейся конструкции
2 Величина и ее измерение	– умение сравнивать предметы по величине и строить упорядоченный ряд;  – умение измерять величину с помощью условной мерки
3 Геометрические фигуры	– представления о геометрических формах, умение их сравнивать;  – умение классифицировать геометрические фигуры по форме, размеру и цвету
4 Пространственные представления	– понимание пространственных отношений;  – умение ориентироваться на листе бумаги;  – умение передвигаться в пространстве, ориентируясь на план-схему
5 Временные представления	– знание названий частей суток, их последовательности и умение определить часть суток по деятельности человека;  – знание названий дней недели и их последовательности;  – умения определять время по часам и выставлять нужное время на часах

 

Оценка каждого показателя сформированности математических представ­лений у старших дошкольников проводилась по следующей шкале:

–     2 балла (высокий уровень) – ребенок самостоятельно и верно выполняет задание, помощь взрослого ему не нужна;

–     1 балл – ребенок выполняет задание при помощи воспитателя, допускает 1-2 ошибки, которые сам исправляет;

–     0 баллов – ребенок не справляется с заданием, допускает более 3 оши­бок, от помощи воспитателя отказывается или она ему не помогает.

Оценивание каждого критерия и общего уровня сформированности мате­матических представлений у детей старшего дошкольного возраста проводилось по сумме баллов, которые смог набрать каждый дошкольник за выполнение всех заданий по пяти критериям. Всего таких заданий 15. Максимальное количество баллов, которое может получить каждый ребенок по всем этим заданиям – 30 (таблица 2, таблица А приложения А).

Таблица 2 – Оценочная шкала уровня сформированности математических представлений у детей старшего дошкольного возраста

 

Критерии	Количество заданий	Уровни/баллы
		высокий	средний	низкий
1 Количественные представления и счет	3	5-6	2-4	0-1
2 Величина и ее измерение	3	5-6	2-4	0-1
3 Геометрические фигуры	3	5-6	2-4	0-1
4 Пространственные представления	3	5-6	2-4	0-1
5 Временные представления	3	5-6	2-4	0-1
Общий уровень	15	23-30	14-22	0-13

 

Анализ уровней сформированности математических представлений у де­тей старшего дошкольного возраста.

Высокий уровень сформированности математических представлений:

–     по критерию «Количественные представления и счет» ребенок самосто­ятельно и правильно умеет соотнести количество с числом пределах от 1 до 8, осуществляет порядковый счет от 1 до 10, правильно оценивает количественную характеристику видоизменяющейся конструкции, то есть понимает, что количе­ство не зависит от пространственного расположения предметов;

–     по критерию «Величина и ее измерение» ребенок самостоятельно срав­нивает предметы по различным величинам и строит упорядоченный ряд, имеет четкие и правильные представления о том, как можно измерить размер предме­тов и их массу, и самостоятельно производит эти измерения с помощью условной мерки;

–     по критерию «Геометрические фигуры» ребенок имеет полные и осо­знанные представления о геометрических формах (квадрат и треугольник), умеет их сравнивать по указанным признакам, правильно классифицирует геометриче­ские фигуры по форме, размеру и цвету;

–     по критерию «пространственные представления» ребенок имеет четкие представления о пространственных отношениях, правильно без помощи взрос­лого называет нахождение предметов в пространстве по словесному образцу с использованием наречий, обозначающих место, умеет самостоятельно ориенти­роваться на листе бумаги и передвигаться в пространстве, ориентируясь на план-схему, постоянно комментируя свои передвижения;

–     по критерию «временные представления» ребенок имеет полные и осо­знанные представления о названиях частей суток, дней недели, времен года, их последовательности, умеет самостоятельно определять время по часам и выстав­лять нужное время на часах.

Средний уровень сформированности математических представлений:

–     по критерию «Количественные представления и счет» ребенок только с помощью взрослого может соотнести количество с числом в пределах от 1 до 8, с одной-двумя ошибками осуществляет порядковый счет от 1 до 10, при помощи взрослого проводит оценку количественной характеристики видоизменяющейся конструкции, то есть у этого ребенка не вполне сформировано понимание того, что количество не зависит от пространственного расположения предметов;

–     по критерию «Величина и ее измерение» ребенок при помощи взрослого сравнивает предметы по различным величинами не с первого раза, а со второй или третьей попытки строит упорядоченный ряд, имеет не вполне четкие и пра­вильные представления о том, как можно измерить размер предметов и их массу, и нуждается в помощи взрослого, чтобы произвести эти измерения с помощью условной мерки;

–     по критерию «Геометрические фигуры» ребенок демонстрирует непол­ные и не вполне осознанные представления о геометрических формах (квадрат и треугольник), их сравнение по указанным признакам производит с помощью взрослого, допускает 1-2 ошибки, не вполне уверенно и с помощью взрослого сравнивает и классифицирует предметы по форме, размеру и цвету;

–     по критерию «пространственные представления» ребенок затрудняется без помощи взрослого назвать нахождение предметов в пространстве; путает по­нятия «справа» и «слева», допускает 1-2 ошибки при ориентации на листе бу­маги, у него не получается передвигаться в пространстве по плану-схеме без до­полнительной помощи взрослого, ребенок затрудняется выразить словами направление своих передвижений;

–     по критерию «временные представления» ребенок знает названия частей суток, дней недели, времен года, но допускает ошибки в их последовательности; по часам правильно определяет, который час, но не может поставить время, ука­занное взрослым на часах (или наоборот).

Низкий уровень сформированности математических представлений:

–     по критерию «количественные представления и счет» ребенок не умеет соотносить количество с числом в пределах от 1 до 8, допускает 3 и более ошибок в порядковом счете в пределах 10: не умеет оценивать количественную характе­ристику видоизменяющейся конструкции, то есть не понимает, что количество не зависит от пространственного расположения предметов;

–     по критерию «величина и ее измерение» ребенок не умеет сравнивает предметы (полоски по длине), не знает названия цветов, не может построить упо­рядоченный ряд; не имеет представлений о том, как можно измерить размер и массу предметов, не может даже при помощи взрослого произвести такие изме­рения;

–     по критерию «геометрические фигуры» ребенок имеет неправильные и неосознанные представления о геометрических формах (квадрат и треугольник), не умеет их сравнивать по указанным признакам; не умеет сравнивать и класси­фицировать предметы по форме, размеру и цвету даже при помощи взрослого;

–     по критерию «пространственные представления» ребенок не может назвать нахождение предметов в пространстве по словесному образцу или по­стоянно при этом ошибается, не умеет ориентироваться на листе бумаги и пере­двигаться в пространстве, ориентируясь на план-схему, не может рассказать о своих передвижениях даже при помощи взрослого;

–     по критерию «временные представления» ребенок плохо знает названия частей суток, дней недели, времен года, допускает ошибки в их последователь­ности; не умеет по часам правильно определять время, не может поставить время на часах.

 Для изучения начального уровня сформированности математических представлений у испытуемых детей 6-7 лет использовались 15 заданий из работ А.В. Белошистой [4, с.18] количественные представления и счет; величина и ее измерение; геометрические фигуры,  З.А. Михайловой и другие (пространствен­ные представления) и Т.Д. Рихтеман [54, с.22] (временные представления) (при­ложение А).

Таким образом, была составлена программа диагностического изучения уровней сформированности математических представлений у детей старшего до­школьного возраста, в которой определены критерии, показатели, даны уровне­вые характеристики сформированности математических представлений у детей, подобраны методики и диагностические задания с наглядным и раздаточным ма­териалом и инструкции к ним по всем критериям изучения математических пред­ставлений детей 5-6 лет.

Далее, проанализированы результаты изучения начального уровня сфор­мированности математических представлений у детей старшего дошкольного возраста и представлены в приложении Б.

Данные, представленные на рисунке 1, показывают, что на начальном этапе работы 25% (5 детей) показали высокий уровень, 55% (11 детей) имеют средний уровень и 20% (4 ребенка) – низкий уровень сформированности количе­ственных представлений и счетной деятельности.

Таким образом, большинство детей показали средний уровень. В ходе ка­чественно анализа полученных результатов установлено, что четверо детей с вы­соким уровнем, выполняя три задания, самостоятельно правильно соотносили количество с числом в пределах от 1 до 8, осуществляли порядковый счет от од­ного до десяти, оценивали количественную характеристику видоизменяющейся конструк­ции.

Четырнадцать детей со средним уровнем выполняли задания постоянно c помощью взрослого, у них не вполне сформировано понимание того, что коли­чество не зависит от пространственного расположения предметов. Двое детей с низким уровнем не справились с заданиями даже при помощи взрослого, они не понимают, что количество не зависит от пространственного расположения пред­метов.

Данные, представленные на рисунке 1, показывают, что на начальном этапе работы 15% (3 ребенка) показали высокий уровень, 75% (15 детей) имеют средний уровень и 10% (2 ребенка) – низкий уровень сформированности пред­ставлений о величинах и способах их измерения. Таким образом, большинство детей показали средний уровень. Качественный анализ полученных данных по­казал, что трое дошкольников с высоким уровнем, выполняя задания, самостоя­тельно сравнили предметы по размеру, с первой попытки построили упорядочен­ный ряд, рассказали, как измерить размер предметов и их массу, и самостоя­тельно провели эти измерения условной меркой. Пятнадцать детей со средним уровнем выполняли задания с постоянной помощью взрослого, построили упо­рядоченный ряд со второй или третьей попытки, неуверенно и неполно расска­зывали о том, как можно измерить размер предметов и их массу, просили по­мощи у воспитателя при измерении длины полосок и массы предметов с помо­щью условной мерки. Двое детей с низким уровнем не справились с заданиями, они даже при помощи взрослого не смогли правильно сравнить полоски по длине, выложить из них лестницу, не знали, как измерить размер и массу пред­метов при помощи условной мерки, воспитателю пришлось показывать, как это нужно сделать.

  Данные, представленные на рисунке 1, показывают, что на начальном этапе работы 15% (3 ребенка) показали высокий уровень, 80% (16 детей) имеют средний уровень и 5% (1 ребенок) – низкий уровень сформированности пред­ставлений о геометрических фигурах. Таким образом, большинство детей пока­зали средний уровень. В ходе качественно анализа полученных результатов уста­новлено, что трое дошкольников с высоким уровнем осознанно применили свои представления о квадрате и треугольнике, нашли их изображения, они правильно провели классификацию геометрических по форме, размеру и цвету. Шестна­дцать детей со средним уровнем имеют неполные и не вполне осознанные пред­ставления о квадрате и треугольнике, допускали ошибки при их сравнении, клас­сифицировали геометрические фигуры по форме, размеру и цвету неуверенно, пользовались помощью взрослого. Один ребенок с низким уровнем назвал все фигуры, но не смог отличить квадрат от прямоугольника, сравнить их между со­бой, с классификацией он тоже не справился, несмотря на активную помощь взрослого.

Данные, представленные на рисунке 1, показывают, что на начальном этапе работы 15% (3 ребенка) показали высокий и низкий уровни, 70%            (14 детей) имеют средний уровень сформированности пространственных пред­став­лений.

Таким образом, большинство детей показали средний уровень. Качествен­ный анализ полученных данных показал, что трое дошкольников с высоким уровнем имеют четкие представления о пространственных отношениях, они пра­вильно назвали нахождение предметов с помощью наречий, при ориентировке на листе бумаги не сделали ни одной ошибки, хорошо ориентируются по плану-схеме, правильно называют направление своих передвижений в пространстве. нахождение предметов в пространстве, путали «право» и «лево», допустили 1-   2 ошибки при ориентации на листе бумаги, просили помощи при чтении план-схемы, не всегда называли направление своих передвижений. Трое детей с низ­ким уровнем постоянно ошибались и путались в назывании местонахождения предметов в пространстве, допустили 3-6 ошибок при ориентировке на листе бу­маги, не смогли сами прочесть план-схему и передвигаться в пространстве, ори­ентируясь на нее, делали это неправильно, молча, никак не обозначая направле­ние своих передвижений по комнате.

Данные, представленные на рисунке 1, показывают, что на начальном этапе работы по15% (по 3 ребенка) имеют высокий и низкий уровни, 70%            (14 детей) показали средний уровень сформированности временных представле­ний. Таким образом, большинство детей показали средний уровень. Трое до­школьни­ков с высоким уровнем продемонстрировали полные (соответствующие про­грамме) и осознанные представления о названиях частей суток, дней недели, вре­мен года, правильно указали их последовательность, умеют самостоятельно определять время по часам и выставлять нужное время на часах, которое указал взрослый. Четырнадцать детей со средним уровнем знают названия частей суток, дней недели, времен года, но допускают ошибки в перечислении их последова­тельности, некоторые из детей правильно определяли время по часам, но не могли поставить время на часах, а некоторые – наоборот. Трое детей с низким уровнем плохо знают названия частей суток, не знают названий некоторых дней недели (вторник, четверг), знают названия времен года, постоянно допускают ошибки, когда нужно назвать их последовательность, не умеют определять время по часам и не могут поставить указанное взрослым время на часах.

 

 

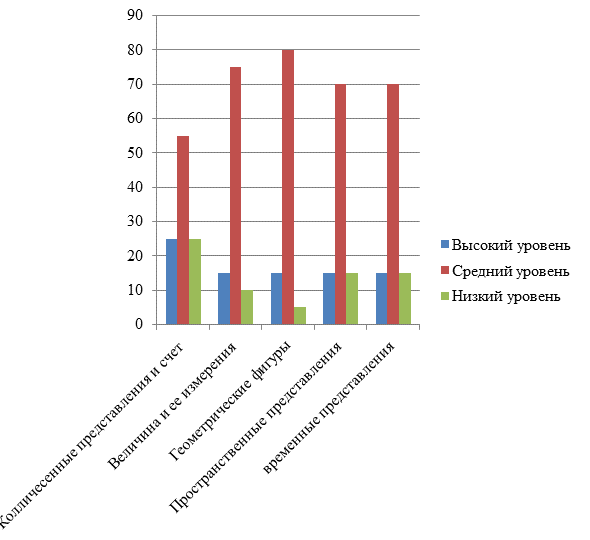
Рисунок 1 – Количественные результаты выявления уровней сформированности математических представлений у детей старшего дошкольного возраста

 

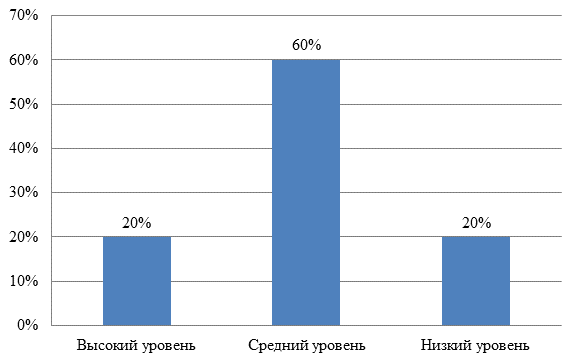
Рисунок 2 – Результаты выявления уровней сформированности математических представлений у детей старшего дошкольного возраста

 

Данные, представленные на рисунке 2, показывают, что на начальном этапе работы у 20% (4 ребенка) обнаружен высокий уровень, у 60% (12 детей) –средний уровень и у 20% (4 ребенка) – низкий уровень. Таким образом, боль­шинство детей показали средний уровень сформированности математических представлений. Такой результат не является удовлетворительным, так как на среднем уровне математические представления детей не вполне соответствуют требованиям образовательной программы по ФЭМП, эти представления фраг­ментарные, отчасти не осознанные, не все дети умеют применять их на практике в новых и нестандартных ситуациях. Все это свидетельствует об актуальности разработки и использования комплекса логико-математических игр в качестве условия формирования элементарных математических представлений у детей старшего дошкольного возраста.

Цель формирующего этапа: разработать и использовать комплекс логико-математических игр как условие формирования математических представлений у детей старшего дошкольного возраста.

Задачи этапа:

–     обучающие задачи: формировать полные, правильные, осознанные, обобщенные и активные количественные, числовые, геометрические, простран­ственные, временные представлений и представления о величинах и их измере­нии, развитие логических приемов мышления (анализ, синтез, сравнение, обоб­щение, классификация, сериация);

–     развивающие задачи: развивать познавательную активность, сенсорное и наглядно-образное восприятие, мышление, память, внимание, речь, положи­тельное отношение к математическому материалу; вызвать, интерес к матема­тике с помощью;

–     воспитательные задачи: воспитывать волевые способности, стремление достигать поставленной цели в процессе познания математических объектов, ре­шения математических задач.

Решение поставленных задач обеспечивал комплекс логико-математиче­ских игр, направленных на формирование математических представлений у де­тей старшего дошкольного возраста. Этот комплекс представлен в приложе-    нии В. Он разработан с учетом требований ФГОС ДО, образовательной про­граммы по математическому развитию детей подготовительной к школе группы, учета возрастных психологических особенностей детей данного возраста.

Комплекс логико-математических игр по формированию математических представлений у детей старшего дошкольного построен на принципах:

–     принцип личностно-ориентированного обучения, то есть опора на инди­видуальные особенности, возможности и интересы каждого ребенка с устране­нием выравнивания детей;

–     принцип системности и целенаправленности в формировании математи­ческих представлений детей;

–     принцип природосообразности, то есть адекватность методов, приемов и форм работы с детьми их возрастным особенностям с преобладанием игровых ситуаций; – принцип от простого к сложному, предполагающий постепенное усложнение содержания и правил игр, формирующих элементарные математи­ческие представления детей;

–     принцип поддержки самостоятельности и инициативы детей, означаю­щий сотрудничество воспитателя и детей, обеспечивающее условия, при кото­рых ребенок не боится высказывать свои мысли, чувства, действовать по соб­ственной инициативе.

Логико-математические игры были подобраны с учетом возрастных осо­бенностей, возможностей и интересов детей старшего дошкольного возраста. Учет возрастных психологических особенностей детей означал, что эти игры, по­мимо формирования элементарных математических представлений у детей, од­новременно развивали наглядно-образное и словесно-логическое виды мышле­ния, сенсорный опыт, произвольность, устойчивость концентрацию, распределя­емость и переключаемость внимания, память, воображение, связную речь, в том числе и математическую. При выборе игр учитывались возможности детей 5-       6 лет, то, что их содержание соответствует требованиям образовательной про­граммы по формированию элементарных математических представлений (далее – ФЭМП) для подготовительной к школе группы, и то, что игровые правила и условия были посильны, понятны и выполнимы для детей, создавали ситуацию успеха, когда в игре победить и выиграть может каждый ребенок. Учет интересов детей означал, что игры выбирались так, чтобы их тематика увлекала детей, со­держание и яркий наглядный игровой материал привлекали внимание детей, цели и задачи игр удовлетворяли стремление детей получить практический ре­зультат: измерить, отсчитать нужное количество, изменить ситуацию на новую, устанавливать связи и зависимости, построить, сконструировать, смоделировать и проявить при этом самостоятельность, инициативу и творчество.

Разработанный комплекс логико-математических игр для детей старшего дошкольного возраста включает 5 групп игр:

–     игры на формирование количественных представлений и счетной дея­тельности;

–     игры на формирование представлений о величинах и способах их изме­рения;

–     игры на формирование представлений о геометрических фигурах и форме предметов;

–     игры на формирование пространственных представлений;

–     игры на формирование временных представлений.

Характеристика каждой группы игр по отдельности.

Первая группа – логико-математические игры на формирование количе­ственных представлений и счетной деятельности обеспечивали:

–     овладение умением соотносить число с количеством: игры «Сколько?» (2 варианта), «Найди пару» (2 варианта), «Бьют часы»;

–     закрепление умения производить порядковый и обратный счет от 1 до 10: игры «Домино», «Математическое лото», «Веселый счет», домино «Веселая зарядка», домино «Белоснежка и семь гномов», «Мои первые цифры». Краткие конспекты игр представлены в приложении В.

 Методика проведения этих игр одинаковая: сначала предлагаются для сравнения предметы в количестве 1, 3 и 5, потом их количество увеличивается до 10. Воспитатель задает детям вопросы и после каждого вопроса просит ре­бенка сосчитать предметы, чтобы доказать ответ: «Каких предметов всего один, каких много? Сосчитай», «Чего больше, чего меньше? Сосчитай».

 Вторая группа – игры на формирование представлений о величинах были направлены на развитие и закрепление у дошкольников умений сравнивать пред­меты по величине (в том числе методами прикладывания и накладывания) и строить упорядоченный ряд: игры «Построй лестницу», «Состав восьмерки», «Коричневая лестница» (палочки Кюизенера).

В игре «Построй лестницу» детям предлагалось выстроить из брусочков сначала большую лестницу для великана, потом – маленькую для гнома, сосчи­тать, сколько палочек в каждой из этих лестниц, найти самую длинную и самую короткую палочку, назвать их цвет. Аналогично ребенок может построить до­мик, кроватки, столы, стулья разных размеров.

Игра «Коричневая лестница» проводилась с помощью логических блоков Дьенеша: десять деревянных призм с квадратным основанием (длина каждой     20 см); размер бокового ребра каждой призмы уменьшается от 10 до 1 см. Детям дается задание – построить лестницу. В ходе игры призмы прикладываются друг к другу в определенной последовательности – от самой толстой к самой тонкой так, чтобы толщина каждой последующей была на 1 см меньше предыдущей. В результате получается лестница, равномерность ступенек которой можно легко увидеть или ощутить руками. В этой игре используется алгоритм построения упорядоченного, сериационного ряда.

Во вторую группу логико-математических игр входят и игры на формиро­вание умений измерять величину и вес с помощью условной мерки: игры «Изме­рим ленту», «Измерь удава», «Весовые качели», «Как измерить пшено в ка­стрюльках», «В каком стакане больше гороха». Конспекты игр представлены в приложении В.

Игровые действия в этих играх – это измерение величины предметов и массы продуктов формирует умение устанавливать численное отношение между измеряемой величиной и заранее выбранной единицей измерения (условной мер­кой), масштабом или эталоном. При этом у детей развиваются логические при­емы мышления – сравнение, обобщение, так как в играх дети измеряют величину нескольких предметов, определяя, какой из них длиннее, выше, шире, толще, или вес нескольких продуктов, определяя, какой из них тяжелее, а какой легче.

Третья группа – игры на формирование представлений о геометрических фигурах и форме предметов способствовали:

–     развитию представлений о геометрических формах и умению их сравни­вать: игры «Чей домик, «Почини ковер-самолет», «Магазин»;

–     формированию и закреплению умению классифицировать геометриче­ские фигуры по форме, величине и цвету: игры «Какой фигуры не хватает?», игры с кругами Эйлера «Непересекающиеся множества», «Пересекающиеся множества», «Три кольца», «Три обруча». Конспекты игр представлены в прило­жении В.

Четвертая группа – игры на формирование пространственных представле­ний обеспечивали:

–     осознание и понимание детьми пространственных отношений и форми­рование, и закрепление умения ориентироваться на листе бумаги по словесной инструкции взрослого: игры «Рисуем фигуры». «Геометрический диктант», «Я еду на машине»;

–     формирование умения передвигаться в пространстве, ориентируясь на словесную инструкцию или план-схему: игры «Синхронное плавание», «Новая походка» «Преодолей лабиринт и проведи друзей».

Пятая группа – игры на формирование временных представлений вклю­чала игры из пособий Т.Д. Рихтерман «Формирование представлений о времени у детей дошкольного возраста» [53, стр.45] и Т.И. Тарабриной и Е.И. Соколовой «Детям о времени» [60,стр.30]:

–     на закрепление представлений детей о названиях частей суток, их после­довательности и умения определить часть суток по деятельности человека: «Что бывает только днем», «Помощник будильника», «Четыре принцессы» – модель частей суток», «Что перепутал художник»;

–     на закрепление представлений детей о названиях дней недели и их по­следовательности: «Живая неделька», «Радужное лото», «Что сначала, что – по­том», «Домик дней»;

–     на формирование умений определять время по часам и выставлять нуж­ное время на часах: «Распорядок дня», «Часы», «Определи, который час», «Нари­суй стрелки у часов» (по словесной инструкции взрослого).

Ведущим видом деятельности в дошкольном возрасте является игра, фор­мирование логико-математических представлений у детей старшего дошколь­ного возраста строится в форме игровых занятий. Для этого использовались ди­дактические игры, головоломки, загадки, занимательные игры и упражнения, ор­ганизуются подвижные игры с познавательным компонентом, игры-исследова­ния. Организовывалось  общение с детьми с целью закрепления и использования полученных знаний; учили  с ними поговорки и пословицы, читали сказки, име­ющие в своем содержании числа; связывающие логико-математические пред­ставления с окружающей жизнью, опытом ребенка (например, предлагалось по­ставить на стол столько чашек, сколько на нем тарелок); объяснялось назначение в жизни людей календаря, часов; знакомили с последовательностью смены ча­стей суток, дней недели, месяцев, времен года; рассматривали  с  детьми  номера домов, ценники в магазинах и так далее, рассматривали с детьми окружающие предметы  в составлении количественной характеристики, сравнении по высоте, ширине, величине и тому подобное.

Выявлялся логико-математический опыт ребенка, что помогало ему в вы­полнении конкретных действий сравнения, разбиения, упорядочивания, класси­фикации, стимулировалась интеллектуальная активность ребенка, побуждая его к проявлению сообразительности, смекалки, к новому поиску вариантов реше­ния задач.

Совместная деятельность со взрослым способствовала продвижению ре­бенка на новый уровень в познании закономерностей, зависимостей и связей, по­строении логических высказываний, стимулировала его интерес к логико-мате­матическим знаниям.

Создавались условия для самостоятельной игровой деятельности детей. Для этого использовались дидактические и настольно-печатные игры, пособия, занимательный материал, различные конструкторы, кубики, мозаики и так далее. Важным условием являлось предоставление ребенку возможности выбора игры, материала, цели, способа решения, оценки своих действий.

Результатом успешной работы по формированию логико-математических представлений у детей старшего дошкольного возраста являлось формирование у ребенка субъектной позиции, развитие активности, инициативности, самосто­ятельности, находчивости, смекалки, стремления к поиску нестандартных реше­ний, ответственности и так далее.

Дидактические игры и упражнения использовались в определенной си­стеме:

–     от простых предметных действий (нахождение, выделение, разделение, группировка) к мыслительным действиям (абстрагирование, сравнение, класси­фикация, обобщение);

–     от действий с одним свойством (цветом, формой, размером) к действиям с двумя, тремя свойствами [39, с.24].

Исходя из основных разделов программы, дидактические игры были пред­ставлены следующими блоками:

–     игры с числами и цифрами («Сколько?», «Какой цифры не стало?», «Назови соседей» и другие;

–     игры на ориентирование в пространстве («Далеко-близко», «Найди клад», «Художник» и другие);

–     игры на ориентирование во времени («Дни недели», «Времена года», «Назови скорее» и другие);

–     игры с геометрическими фигурами («Геометрическое лото», «Чудесный мешочек», «Найди предмет такой же формы», «Назови геометрическую фигуру» и другие);

–     игры с величинами («Разложи по размеру», «Больше – меньше», «Рас­ставь по порядку» и другие).

Основными дидактическими пособиями, способствующими логико-мате­матическому развитию дошкольников, являлись логические блоки Дьенеша, па­лочки Кюизенера, игры В.В. Воскобовича, Б.П. Никитина, игры-головоломки.

Благодаря их использованию процесс формирования логико-математиче­ских представлений у детей проходит в доступной и привлекательной форме. Игры В.В. Воскобовича, Б.П. Никитина «Геоконт», «Квадрат», «Сложи узор», «Кубики» можно предложить детям во время самостоятельной деятельности, ис­пользовать при индивидуальной работе и в непосредственно образовательной деятельности. Также можно рекомендовать эти игры для развития логико-мате­матических представлений у ребенка в семье – для игры с родителями или дру­зьями. Большие возможности для формирования логико-математических пред­ставлений имеются в играх «Танграм», «Волшебный круг», «Колумбово яйцо», «Кубики для всех» и другие.

Дети могут использовать не только один, но и 2-3 набора для создания но­вых, более сложных силуэтов. Особое место занимают игры на составление плос­костных изображений предметов, животных, птиц, домов из специальных набо­ров геометрических фигур. Наборы фигур при этом представляют собой части, разрезанной определенным образом фигуры: треугольника, квадрата, овала, круга. Детей увлекает результат составить увиденное по образцу, и они активно включаются в практическую деятельность по подбору способа расположения фигур с целью создания силуэта.

Для стимулирования коллективных игр и творческой деятельности исполь­зуются фланелеграфы с наборами фигур, магнитные доски, счетные палочки, альбомы для зарисовки придуманных задач, составления фигур.

Большой интерес у детей старшего дошкольного возраста вызывают голо­воломки, игры на смекалку, занимательные игры. Интерес детей к головоломкам может поддерживаться за счет веревочных головоломок, игр на передвижение, использования игр-головоломок со счетными палочками (спичками) они называ­ются задачами на смекалку геометрического характера. В ходе их решения идет трансфигурация, преобразование одних фигур в другие, а не только изменение их количества. Из наборов обычных счетных палочек, составляются наглядные задачи-головоломки. Также использовались таблицы с графически изображен­ными на них фигурами, которые подлежат преобразованию. С обратной стороны таблицы указывается, какое преобразование надо проделать и какая фигура должна в результате получиться. На таких занятиях формируются важные каче­ства личности ребенка: наблюдательность, самостоятельность, находчивость, со­образительность, вырабатывается усидчивость, развиваются конструктивные умения. Для формирования и развития логико-математических представлений у детей используют разнообразные виды логических упражнений и задач. К ним относятся задачи на продолжение ряда фигур, нахождение пропущенной фи­гуры, на поиск закономерностей, чисел, задачи типа на поиск недостающей в ряду фигуры (нахождение закономерностей, лежащих в основе выбора этой фи­гуры) и тому подобное. Например «Какое число надо поставить в пустую клетку?», «Какая из фигур здесь лишняя и почему?», «Четвертый лишний» и так далее. Назначение логических упражнений и задач состоит в активации умствен­ной деятельности детей, в оживлении процесса обучения.

Учитывая важность и сложность формирования у детей старшего дошколь­ного возраста логико-математических представлений, педагогам необходимо не только использовать дидактические игры и пособия в своей работе с детьми, но рекомендовать их родителям воспитанников для работы с детьми дома. Для этого проводятся консультации, мастер-классы, практические показы и демон­страция возможностей использования игрового материала.

Цель контрольного этапа – выявить эффективность применения логико-ма­тематических игр в формировании элементарных математических представле­ний у детей старшего дошкольного возраста.

Задачи этапа:

–     провести итоговую диагностику уровней сформированности математи­ческих представлений у детей, обработать полученные результаты;

–     дать сравнительный анализ результатов обследования детей до и после использования комплекса логико-математических игр. Итоговая диагностика де­тей старшего дошкольного возраста осуществлялась по тем же критериям, пока­зателям, уровням и с помощью тех же методик и диагностических заданий, ко­торые использовались при проведении начальной диагностики. Результаты ито­говой диагностики детей занесены в сводный протокол 2 (приложение Г).

Сравнительные результаты сформированности математических представ­лений по критерию «Количественные отношения и счет» у детей на начальном и итоговом этапах работы представлены на рисунке 3.

Данные рисунка 3 показывают, что у детей имеется положительная дина­мика в формировании математических представлений по критерию «количе­ственные отношения и счет». После реализации комплекса логико-математиче­ских игр увеличилось количество детей с высоким уровнем (было 25% – 5 чело­век, стало 35% – 7 человек), не изменилось количество детей со средним уровнем (было 55% – 11 человек), детей с низким уровнем (вначале было 20% – 4 чело­века, стало 10% – 2 человека).

 

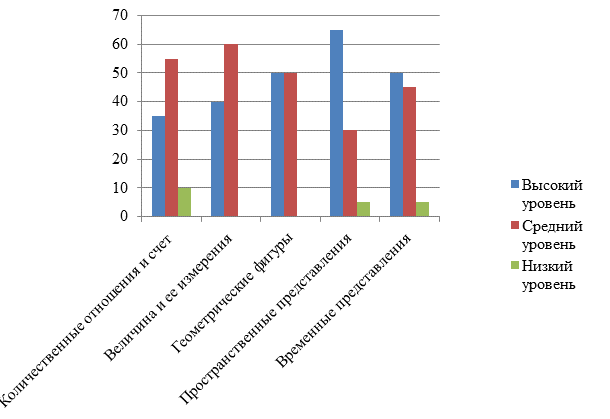
Рисунок 3 – Сравнительные результаты сформированности математических представлений по критерию «количественные отношения и счет» у детей на начальном и итоговом этапах работы

 

Это говорит о том, что количественные представления детей стали соот­ветствовать программным требованиям, большинство дошкольников осознанно научились осознанно соотносить количество с числом, без ошибок осуществлять порядковый и обратный счет от 1 до 10, давать количественную характеристику видоизменяющейся конструкции, то есть дети хорошо поняли, что количество не зависит от пространственного расположения предметов.

Сравнительные результаты сформированности математических представ­лений по критерию «величина и ее измерение» у детей на начальном и итоговом этапах работы представлены на рисунке 3. Они показывают, что у детей имеется положительная динамика в формировании математических представлений по критерию «величина и ее измерение».

После реализации комплекса логико-математических игр увеличилось ко­личество детей с высоким уровнем (было 15% – 3 человека, стало 40% – 8 чело­века), уменьшилось количество детей со средним уровнем (было 75% – 15 чело­век, осталось 60% – 12 человек), не осталось детей с низким уровнем (вначале было 10% – 2 человека).

Эти положительные изменения отразились в качестве представлений детей о величине и способах ее измерения: большинство детей научились самостоя­тельно сравнивать предметы по величине, строить упорядоченный ряд, у них имеются четкие и правильные представления о том, как можно измерить размер предметов и их массу, поэтому они правильно производят эти измерения с помо­щью условной мерки.

Сравнительные результаты сформированности математических представ­лений по критерию «форма предметов» у детей на начальном и итоговом этапах работы представлены на рисунке 3.

Данные рисунка 3 показывают положительную динамику в формировании математических представлений у старших дошкольников по критерию «геомет­рические фигуры». После реализации комплекса логико-математических игр увеличилось количество детей с высоким уровнем (было 15% – 3 человека, стало 50% – 10 человек), уменьшилось количество детей со средним уровнем (было 80% – 16 человек, осталось 50% – 10 человек), не осталось детей с низким уров­нем (вна­чале было 5% – 1 человек).  Эти положительные изменения показывают, что у большинства дошкольников имеются полные и осознанные представления о гео­метрических формах, дети по указанным признакам умеют отличать квад­раты от треугольников, правильно классифицируют геометрические фигуры по форме, размеру и цвету.

Сравнительные результаты сформированности математических представ­лений по критерию «пространственные представления» у детей на начальном и итоговом этапах работы представлены на рисунке 3.

Данные, представленные на рисунке 3, свидетельствуют о положительной динамике в формировании математических представлений у старших дошколь­ников по критерию «пространственные представления». После реализации ком­плекса логико-математических игр увеличилось количество детей с высоким уровнем (было 15% – 3 человека, стало 65% – 13 человек),  уменьшилось коли­че­ство детей со средним уровнем (было 70% – 14 человек, осталось 30% – 6 че­ловек),  детей с низким уровнем (вначале их было 15% – 3 человека, осталось 5% – 1 чело­век).  Это говорит о том, что пространственные представления детей стали более полными, осознанными, соответствующими программным требова­ниям. Дети научились правильно определять местонахождение предметов в про­странстве, обозначать его с помощью наречий, самостоятельно ориентироваться на листе бумаги и передвигаться в пространстве, ориентируясь на план-схему, постоянно комментируя свои передвижения.

Сравнительные результаты сформированности математических представ­лений по критерию «временные представления» у детей на начальном и итого­вом этапах работы представлены на рисунке 3.

Данные, представленные на рисунке 3, показывают положительную дина­мику в формировании математических представлений у старших дошкольников по критерию «временные представления». После реализации комплекса логико-математических игр увеличилось количество детей с высоким уровнем (было 15% – 3 человек, стало 50% – 10 человек),  уменьшилось количество детей со сред­ним уровнем (было 70% – 14 человек, осталось 45% – 9 человек),  детей с низким уров­нем (вначале их было 15% – 3 человека, осталось 5% – 1 человек). Качество времен­ных представлений у детей возросло, что проявилось в том, что большинство де­тей стали демонстрировать полные, осознанные и активные представления о названиях частей суток, дней недели, времен года, их последо­вательности, умеют самостоятельно определять время по часам и выставлять нужное время на часах.          

Сравнительные результаты сформированности математических представ­лений у детей старшего дошкольного возраста на начальном и итоговом этапах работы представлены на рисунке 4.

Данные, представленные на рисунке 4, показывают, что у дошкольников имеется положительная динамика в формировании математических представле­ний. После реализации комплекса логико-математических игр увеличилось ко­личество детей с высоким уровнем (было 20% – 4 человека, стало 40% – 8 чело­век),  изменилось количество детей со средним уровнем (было 65% – 13 человек, осталось 50% – 7 человек), уменьшилось детей с низким уровнем (в начале ра­боты их было 20% – 4 человека, осталось 10% – 2 человека).

 

 

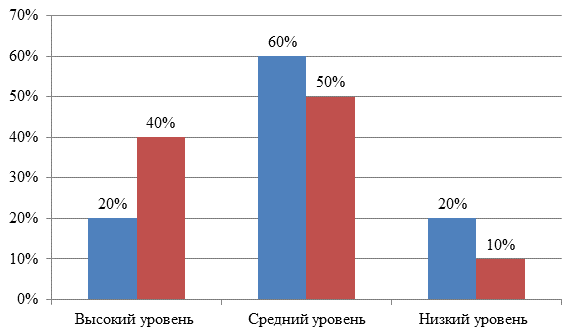
Рисунок 4 – Сравнительные результаты сформированности математических представ­лений у детей старшего дошкольного возраста на начальном и итоговом этапах работы

 

Таким образом, результаты, полученные на контрольном этапе, показали, что у детей отмечается положительная динамика в уровне сформированности элементарных математических представлений. Это показывает эффективность реализованных логико-математических игр и доказывает, что их использование является важным условием для формирования количественных, счетных, гео­метрических, пространственных, временных представлений, представлений о ве­личине и форме предметов у детей старшего дошкольного возраста.

 

 

ЗАКЛЮЧЕНИЕ

 

В ходе проведенного исследования были получены следующие резуль­таты.

В ходе изучения нормативно-законодательной, психолого-педагогической и методической литературы по проблеме исследования установлено, что разра­ботка содержания математического образования детей дошкольного возраста за последние десятилетия показала, что содержание математических представле­ний детей составляют количественные и счетные представления, представления о величинах и их измерении, о форме предметов и геометрических фигур, про­странственные и временные представления. Важным направлением в формиро­вании математических представлений старших дошкольников является овладе­ние логическими приемами мыслительной деятельности.

Анализ литературы показал, что к психолого-педагогическим особенно­стям формирования математических представлений у детей старшего дошколь­ного возраста относятся:

–     сенсорная основа формирования этих представлений, достаточный уро­вень развития восприятия, наглядно-образного мышления, внимания, памяти, воображения и речи детей;

–     овладение логическими приемами мышления;

–     выполнение программных задач и программного содержания по форми­рованию элементарных математических представлений у детей.

Учет этих особенностей позволил выделить в качестве одного из главных условий, обеспечивающих успешность формирования элементарных математи­ческих представлений у старших дошкольников, разработку и внедрение ком­плекса логико-математических игр.

Игра – ведущий вид деятельности в дошкольном возрасте, которая обла­дает большим педагогическим потенциалом для личностного развития дошколь­ников и достижения образовательных результатов по всем образовательным об­ластям дошкольного образования, в том числе – и по формированию элементар­ных математических представлений. Сущность игры – обучение, воспитание и развитие детей. В существующих сегодня классификациях виды игр для до­школьников разнообразны: сюжетные, дидактические, подвижные, театрализо­ванные, досуговые и так далее. Каждый вид имеет свои особенности, отличается условиями организации, целью и задачами. Роль игр в формирование математи­ческих представлений у детей старшего дошкольного возраста состоит в том, что они способствуют сенсорному развитию детей, которое выступает основой ум­ственного воспитания дошкольников.

Игры с логико-математическим содержанием предусматривают обучение детей счету, освоению свойств и отношений, формирование логических приемов мышления, совершенствование речи, развитие умений ориентироваться во вре­мени и пространстве. По видам эти игры разнообразны: наглядно-печатные, сло­весные, конструкторские, подвижные. Их применение в процессе формирования элементарных математических представлений у детей старшего дошкольного возраста предполагает, что они должны содержать элемент новизны, формиро­вать новые для детей математические представления и умения; воспитатель на первых этапах руководит этими играми и принимает в них активное участие.

Исследование включало констатирующий, формирующий и контрольный этапы. В нем принимали участие 20 детей старшой   группы в возрасте 5-6 лет.

В практической части работы описан диагностический инструментарий для выявления уровней сформированности математических представлений у де­тей старшего дошкольного возраста.

Он включает пять критериев и соответствующие им показатели, уровневые характеристики, диагностические методики и задания по каждому критерию:

–     количественные представления и счет;

–     величина и ее измерение;

–     геометрические фигуры;

–     пространственные представления;

–     временные представления. эти критерии соответствуют требованиям об­разовательной программы по математическому образованию детей 5-6 лет.

В результате констатирующего этапа исследования было установлено, что у детей старшего дошкольного возраста преобладающим является средний уро­вень сформированности математических представлений. Такой результат не яв­ляется удовлетворительным, так как, имея этот уровень, дошкольники обладают не вполне полными (соответствующими программным требованиям), осознан­ными, обобщенными представлениями, не умеют применять их на практике в новых и нестандартных ситуациях.

Это сделало актуальным разработку и использование комплекса логико-математических игр по формированию математических представлений у детей старшего дошкольного возраста. Этот комплекс разработан с учетом требований ФГОС ДО, образовательной программы по математическому развитию детей подготовительной к школе группы, учета возрастных психологических особен­ностей детей данного возраста. Он основан на принципах личностно-ориентиро­ванного обучения, системности и целенаправленности, от простого к сложному, поддержки активности, самостоятельности и инициативы детей. Логико-матема­тические игры подобраны с учетом возрастных особенностей, возможностей и интересов детей старшего дошкольного возраста, для их использования в группе детского сада была создана эффективная развивающая предметно-простран­ственная среда.

Результаты контрольного этапа показали положительную динамику уровня сформированности математических представлений у старших дошколь­ников. Это дает  основание для вывода о том, что  логико-математические игры являются важным условием для успешного формирования математических пред­ставлений у детей старшего  дошкольного возраста,  эффективны для формиро­вания количественных, числовых, геометрических, пространственных, времен­ных представлений и представлений о форме, величине предметов и способах их измерений.

Таким образом, цель работы достигнута, задачи полностью решены, гипо­теза подтвердилась

 

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

 

1     Аванесова В.Н. Дидактические игры и занятия в самостоятельной де­я-тельности детей // Сенсорное воспитание в детском саду / Под ред. Н.Н. Под-дьякова, В.Н. Аванесовой. М.: Просвещение, 2021. С. 84-103.

2     Агапова И.А. Театральные занятия и игры в детском саду: развиваю­щие упражнения, тренинги, сценарии. М.: Лада, 2021. 224 с.

3     Арапова-Пискарева Н.А. Формирование элементарных математиче­ских представлений в детском саду: программа и метод. рекомендации: для занятий с детьми 2-7 лет. М.: Мозаика-Синтез, 2019. 243 с.

4     Белошистая А.В. Диагностика математического развития детей до­школьного возраста. М.: Владос, 2017. 135 с.

5     Белошистая А.В. Обучение математике в дошкольных образователь­ных организациях. М.: Инфра-М, 2019. 320 с.

6     Белошистая А.В. Развитие логического мышления у дошкольников. М.: Инфра-М, 2019. 300 с.

7     Белошистая А.В. Развитие математического мышления ребенка до­школьного и младшего школьного возраста в процессе обучения. М.: Инфра-М, 2018. 234 с.

8     Белошистая А.В. Тесты для проверки математических способностей де­тей 6-7 лет. М.: Айрис-Пресс, 2019. 24 с. 

9     Белошистая А.В. Формирование и развитие математических способ­но­стей дошкольников.  М.: Владос, 2021. 400 с.

10     Богуславская 3.М. Развивающие игры для детей младшего дошколь­ного возраста. М.: Просвещение, 2021. 207 с.

11     Богуславская З.М. Психологические особенности познавательной дея­тельности дошкольников в условиях дидактической игры // Психология и педа­гогика игры дошкольника: материалы симпозиума / Под ред. А.В. Запо­рожца, А.П. Усовой. М.: Просвещение, 2016. С. 23-31.

12     Бондаренко А.К. Дидактические игры в детском саду. М.: Просвеще­ние, 2017. 160 с.

13     Воронина Л.В. Теория и технологии математического образования де­тей дошкольного возраста. Екатеринбург: Урал. гос. пед. ун-т, 2020. 282 с.

14     Выготский Л.С. Педагогическая психология. М.: АСТ, 2018. 671 c.

15     Гальперин П.Я. Введение в психологию. М.: Апрель, 2016. 331 с.

16     Гурова Л.Л. Психология мышления. М.: ПЕР СЭ, 2021. 136 с.

17     Давыдов В.В. Теория развивающего обучения. М.: ИНТОР, 2018. 544 с.

18     Данилова В.В. Обучение математике в детском саду / Авт.-сост.         В.В. Данилова, Т.Д. Рихтерман, З.А. Михайлова. М.: Академия, 2018. 160 с. 

19     Детство: пример. образоват. программа дошкол. образования / Авт.-сост. Т.И. Бабаева, А.Г. Гогоберидзе, О.В. Солнцева. СПб.: Детство-Пресс, 2021. 321 с.

20     Дидактические игры и упражнения по сенсорному воспитанию до­школьников / Под ред. Л.А. Венгера. М.: Просвещение, 2018. 96 с.

21     Дидактические игры, направленные на развитие логического мыш­ле­ния у дошкольников: [Электронный ресурс]. URL: https://nsportal.ru/detskiy-sad/raznoe/2012/-02/15/didakticheskie-igry-napravlennye-na-razvitie-logicheskogo-myshleniya-u (дата обращения 27.12.2022).

22     Запорожец А.В. Избранные психологические труды: в 2 т. Т. 1. М.: Пе­дагогика, 2018. 516 с.

23     Ивакина И.О. Руководство творческими сюжетно-ролевыми играми до­школьников. Пенза: ПГПУ, 2020. 64 с.

24     Игра дошкольника / Под ред. С.Л. Новоселовой. М.: Просвещение, 2019. 286 с.

25     Игры на развитие логического мышления для детей 5-6 лет в детском саду: [Электронный ресурс]. URL: http://ped-kopilka.ru/igry-konkursy-razvleche-nija/razvivayuschie-igry-dlja-doshkolnikov/igry-na-razvitie-logicheskogo-myshlenija-dljadetei-5-6-let-v-detskom-sadu.htm (дата обращения 27.12.2022).

26     Калиниченко А.В. Развитие игровой деятельности дошкольников. М.: Айрис-Пресс, 2021. 112 с.

27     Касаткина Е.И. Игра в жизни дошкольника. М.: Дрофа, 2010. 176 с.

28     Колесникова Е.В. Обучение решению арифметических задач. М.: ТЦ Сфера, 2018. 64 с.

29     Комарова О.А. Наполнение развивающей среды ДОО в соответствии с образовательными областями // Справочник старшего воспитателя. 2020. №8.    С. 41-43.

30     Концепция развития математического образования в Российской Фе­де­рации: утв. распоряжением Правительства Рос. Федерации от 24 дек. 2013 г. №2506-р.: [Электронный ресурс]. URL: http://www.firo.ru/wpcontent/uploads/ 2014/12/Concept_mathematika.pdf (дата обращения 27.12.2022).

31     Корнеева Г.А. Методика формирования элементарных математиче­ских представлений у детей. М.: Просвещение, 2019. 56 с.

32     Кудыкина Н. В. Дидактические игры и занимательные задания для пер­вого класса четырехлетней начальной школы. Киев: Радян. шк., 2019. 300 с.

33     Лебеденко Е.Н. Формирование представлений о времени у дошколь­ни­ков. СПб.: Детство-Пресс, 2018. 320 с.

34     Леонтьев А.Н. Психологические основы дошкольной игры // Избран­ные психологические произведения: в 2 т. Т. 1. М.: Педагогика, 2019. 580 с.

35     Леушина А.М. Теория и методика формирования элементарных ма­те­матических представлений у детей дошкольного возраста. М.: Просвещение, 2021. 368 с.

36     Макарова И.В. Общая психология: крат. курс лекций. М.: Юрайт, 2018. 382 c.

37     Маневцова Л.М. Формирование системных знаний о сезонных изме­не­ниях в жизни животных у детей старшего дошкольного возраста. СПб.: СПбГУ, 2019. 279 с.

38     Математика до школы / Сост. А.А. Смоленцева, А.В. Пустовойт,        З.А. Михайлова, Р.Л. Непомнящая. СПб.: Акцидент, 2017. 189 с.

39     Михайленко Н.Я. Игра с правилами в дошкольном возрасте. М.: Акад. Проект, 2022. 260 с.

40     Мусейибова Т.А. Формирование некоторых пространственных ори­ен­таций // Теория и методика развития элементарных математических пред­ставле­ний у дошкольников: хрестоматия: в 6 ч. Ч. 4-6 / Сост. 3.А. Михайлова,                Р.Л. Непомнящая. СПб.: Питер, 2018. С. 35-49.

41     Мухина В.С. Возрастная психология: феноменология развития. М.: Академия, 2020. 656 с.

42     Нищева Н.В. Игры для формирования представлений о времени у де­тей дошкольного возраста. СПб.: Детство-Пресс, 2020. 32 с.     

43     Носова Е.А. Логика и математика для дошкольников. СПб.: Акци­дент, 2016. 79 с.

44     Об образовании в Российской Федерации: федер. закон № 273-ФЗ: [принят Гос. Думой 21 дек. 2012 г.  одобрен Советом Федераций 26 дек. 2012 г.]: [Электронный ресурс]. URL: http://www.consultant.ru/document/-cons_doc_ LAW_140174/ (дата обращения 06.03.2023).

45     Обухова Л.Ф. Возрастная психология. М.: Юрайт, 2019. 460 с.

46     От рождения до школы: основ. общеобразоват. программа дошкол. об­разования / Под ред. Н.Е. Вераксы. М.: Мозаика-Синтез, 2014. 304 с.

47     Павлова Л.И. Теория и методика развития математических представ­ле­ний у дошкольников. М.: МПГУ, 2017. 106 с. 

48     Палочки Кюизенера: [Электронный ресурс]. URL: https://razvivashka. online/metodiki/-palochki-kyuizenera (дата обращения 26.04.2023).

49     Педагогика / Под ред. Л.С. Подымовой, В.А. Сластенина. М.: Юрайт, 2018. 246 с.

50     Перова М.Н. Дидактические игры и упражнения по математике для ра­боты с детьми дошкольного и младшего школьного возраста. М.: Просвеще­ние, 2018. 144 с.

51     Поддьяков Н.Н. Новые подходы к исследованию мышления до­школь­ников // Вопросы психологии. 2020. № 2. С. 18-26.

52     Помораева И.А. Формирование элементарных математических пред­ставлений: система работы в подгот. к шк. группе дет. сада. М.: Мозаика-Син­тез, 2019. 176 с.

53     Радуга: пример. основ. образоват. программа дошкол. образования / Авт.-сост. С.Г. Якобсон, Т.И. Гризик, Т.Н. Доронова. М.: Просвещение, 2018.  232 с.

54     Развитие мышления и умственное воспитание дошкольника / Под ред. Н.Н. Поддьякова, А.Ф. Говорковой. М.: Педагогика, 2019. 200 с.

55     Рихтерман Т.Д. Формирование представлений о времени у детей до­школьного возраста. М.: Просвещение, 2021. 183 с.

56     Рубинштейн С.Л. Основы общей психологии. СПб.: Питер, 2019. 705 с.

57     Сенсорное воспитание в детском саду / Под ред. Н.Н. Поддьякова,    В.Н. Аванесовой. М.: Просвещение, 2021. 192 с.

58     Столяр А.А. Давайте поиграем: математические игры для детей 5-6 лет. М.: Просвещение, 2021. 84 с.

59     Тарабрина Т.И. Детям о времени. Ярославль: Академия развития, 2016. 237 с.

60     Тарунтаева Т.В. Развитие элементарных геометрических представле­ний дошкольников. М.: Просвещение, 2017. 64 с.

61     Теории и технологии математического развития детей дошкольного возраста / Авт.-сост. З.А. Михайлова, Е.Д. Носова, А.А. Столяр. СПб.: Дет­ство-Пресс, 2018. 376 с.

62     Теория и методика развития элементарных математических пред­став­лений у дошкольников: хрестоматия: в 6 ч. Ч. 1 / Сост. 3.А. Михайлова,               Р.Л. Непомнящая. СПб.: Питер, 2018. 234 с.

63     Тимофеева Е.А. Подвижные игры с детьми дошкольного возраста. М.: Просвещение, 2019. 120 с.

64     Тихеева Е.И. Игры и занятия малых детей. СПб.: Питер, 2019. 103 с.

65     Тихомиров О.К. Психология мышления. М.: Академия, 2017. 287 с.

66     Урунтаева Г.А. Детская психология. М.: Академия, 2018. 336 с.

67     Фаусек Ю. Детский сад Монтессори. М.: Карапуз-Дидактика, 2017.   240 с.

68     Федеральный государственный образовательный стандарт дошколь­ного образования. М.: Аспект-плюс, 2017. 38 с.

69     Формирование элементарных математических представлений у до­школьников / Под ред. А.А. Столяра. М.: Просвещение, 2018. 302 с.

70     Шадриков В.Д. Общая психология. М.: Юрайт, 2016. 411 c. 

71     Шапарь В.Б. Новейший психологический словарь. Ростов-н/Д.: Фе­никс, 2015. 806 с.

72     Щербакова Е.И. Методика обучения математике в детском саду. М.: Академия, 2020. 272 с.

73     Щербакова Е.и. Теория и методика математического развития до­школьников. М.: Изд-во Моск. психол.-социал. ин-та; Воронеж: МОДЭК, 2019. 392 с.

74     Эльконин Д.Б. Детская психология. М.: Академия, 2017. 384 с.

75     Эльконин Д.Б. Психология игры. М.: Владос, 2019. 360 с.

ПРИЛОЖЕНИЕ А

(справочное)

 

Диагностический инструментарий для оценки уровней сформированности математических представлений у детей старшего дошкольного возраста

(6-7 лет)

 

Критерий 1. «Количественные представления и счет».

Задание 1

Цель: выявить умение соотносить количество с числом в пределах от 1      до 8.

Форма проведения – индивидуальная.

Материал: карточки с изображением 8 кругов и 7 квадратов.

Методика проведения. Воспитатель просит ребенка сосчитать, сколько на карточке изображено кругов (8 кругов расположены в беспорядке). Потом сосчи­тать, сколько на другой карточке квадратов (7 квадратов, расположены в ряд) и ответить на вопрос: «Где фигур больше; там, где 8, или там, где 7»?

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который самостоятельно и правильно сумел соотнести количество с числом в пределах от 1 до 8;

–     средний уровень (1 балл) получает ребенок, у которого с первого раза не получилось правильно соотнести количество с числом в пределах от 1 до 8, по­требовалась помощь воспитателя;

–     низкий уровень (0 балл) получает ребенок, который не умеет соотносить количество с числом в пределах от 1 до 8.

Задание 2

Цель: определить умение производить порядковый и обратный счет в пре­делах 10.

Форма проведения – индивидуальная.

Материал: карточка с изображением 9 кругов, 12 кубиков.

Продолжение приложения А

 

Методика проведения. Воспитатель просит ребенка положить на стол ку­биков на 1 больше, чем кружков на карточке (кружков на карточке 9). После этого просит ребенка сосчитай кубики в прямом порядке, а потом в обратном.

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который правильно счи­тает по порядку и производит обратный счет в пределах 10;

–     средний уровень (1 балл) получает ребенок, который допускает1-2 ошибки в порядковом и обратном счете в пределах 10;

–     низкий уровень (0 балл) получает ребенок, который допустил 3 и более ошибок в порядковом и обратном счете в пределах 10.

Задание 3

Цель: выявить умение оценивать количественную характеристику видоиз­меняющейся конструкции (без изменения количества элементов).

Форма проведения – индивидуальная.

Материал: 4 счетные палочки, из которых выложен квадрат.

Методика проведения. Воспитатель дает ребенку инструкцию: «Верхнюю палочку переложим вот так (верхнюю сдвигает палочку вниз, чтобы она оказа­лась посередине вертикально лежащих палочек). Скажи, изменилось ли количе­ство палочек? Почему не изменилось?». (Палочку переставили, но не убрали и не добавили).

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который правильно оцени­вает количественную характеристику видоизменяющейся конструкции;

–     средний уровень (1 балл) получает ребенок, которому понадобилась по­мощь воспитателя при оценивании количественной характеристики видоизменя­ющейся конструкции;

–     низкий уровень (0 балл) получает ребенок, который не умеет оценивать количественную характеристику видоизменяющейся конструкции.

Продолжение приложения А

 

Критерий 2. «Величина и ее измерение»

Задание 1

Цель: выявить умение сравнивать предметы по величине и строить упоря­доченный ряд.

Форма проведения – индивидуальная.

Материал: 6 полосок одинаковой ширины, но различные по длине и цвету.

Методика проведения. Воспитатель просит ребенка:

–     сравнить полоски по длине и разложи их одну под другой – от самой короткой до самой длинной, чтобы получилась лесенка;

–     сказать, какого цвета самая длинная полоска, какого цвета самая корот­кая.

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который самостоятельно правильно сравнивает предметы (полоски по длине), знает названия цветов, строит упорядоченный ряд (лесенки из полосок разной длины);

–     средний уровень (1 балл) получает ребенок, у которого не получается самостоятельно сравнить полоски по длине, допускает 1-2 ошибки в названии цветов и построении упорядоченного ряда;

–     низкий уровень (0 балл) получает ребенок, который не умеет сравнивает предметы (полоски по длине), не знает названия цветов, не может построить упо­рядоченный ряд.

Задание 2

Цель: определить умение измерять величину с помощью условной мерки.

Форма проведения – индивидуальная.

Материал: условная мерка – палочка длиной 10 см; стол.

Методика проведения. Воспитатель задает ребенку вопросы: «Скажи, как определить длину предметов?», «Скажи, чем можно измерить ширину (длину)?». Затем дает ребенку задание: измерить длину стола этой меркой. (Дает ребенку

Продолжение приложения А

 

палочку, которая уложится в длине стола без остатка).

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который имеет четкие и правильные представления о том, как можно измерить величину предметов и 95 самостоятельно производит эти измерения с помощью условной мерки;

–     средний уровень (1 балл) получает ребенок, который неуверенно отве­чает, как можно измерить величину предметов и у которого не получается са­мому измерить длину стола с помощью условной мерки, ему нужна помощь взрослого;

–     низкий уровень (0 балл) получает ребенок, который не имеет представ­лений о том, как можно измерить величину предметов и не может даже при по­мощи взрослого произвести такие измерения.

Задание 3

Цель: выявить умение измерять массу.

Форма проведения – индивидуальная.

Материал: крупа в мешочке; вода в пластмассовом графине, пластмассо­вые стаканчики для измерения.

Методика проведения. Воспитатель задает ребенку вопросы: «Скажи, чем можно измерить крупу в мешочке? А воду в графине?». Затем просит ребенка сделать эти измерения.

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который имеет четкие, осо­знанные и правильные представления о том, как можно измерить массу предме­тов и самостоятельно производит эти измерения с помощью условной мерки;

–     средний уровень (1 балл) получает ребенок, который имеет нечеткие и неосознанные представления о том, как можно измерить массу предметов и из­меряет массу только с помощью взрослого;

–     низкий уровень (0 балл) получает ребенок, который не представляет, как

Продолжение приложения А

 

можно измерить массу предметов и не может измерить массу даже при помощи взрослого.

Критерий 3. «Геометрические фигуры»

Задание 1

Цель: выявить представления о геометрических формах (квадрат и тре­угольник), умение сравнивать геометрические фигуры по указанным признакам.

Форма проведения – индивидуальная.

Материал: карточка с контурным изображением квадрата, треугольника, четырехугольника и пяти угольника.

Методика проведения. Воспитатель просит ребенка обвести по контуру каждую фигуру. Сосчитать, сколько углов в каждой фигуре. Отметить квадрат одной галочкой, а треугольник – двумя галочками. Оставшиеся фигуры раскра­сить в синий цвет.

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который имеет полные и осознанные представления о геометрических формах (квадрат и треугольник), умеет их сравнивать по указанным признакам;

–     средний уровень (1 балл) получает ребенок, у которого имеются непол­ные и не вполне осознанные представления о геометрических формах (квадрат и треугольник), нуждается в помощи взрослого для сравнения 96 геометрических фигур по указанным признакам;

–     низкий уровень (0 балл) получает ребенок, который имеет неправильные и неосознанные представления о геометрических формах (квадрат и треуголь­ник), не умеет их сравнивать по указанным признакам.

Задание 2

Цель: определить умения сравнивать и классифицировать геометрические фигуры по форме.

Форма проведения – индивидуальная.

Продолжение приложения А

 

Материал: рисунок с изображением 10 четырехугольников, среди которых 5 совершенно одинаковых квадратов и 5 четырехугольников, немного отличаю­щихся от квадратов: вертикальные стороны чуть длиннее горизонтальных, или наоборот, какой-либо из углов четырехугольника меньше или больше прямого угла.

Методика проведения. Воспитатель просит ребенка найти и показать все одинаковые фигуры (квадраты, у которых все стороны и углы равны).

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который отыскал 4-5 квад­ратов;

–     средний уровень (1 балл) получает ребенок, который нашел 2-3 квад­рата;

–     низкий уровень (0 балл) получает ребенок, который указал 1 квадрат или не нашел ни одного квадрата.

Задание 3

Цель: выявить умение сравнивать и классифицировать предметы по форме, размеру и цвету. Форма проведения – индивидуальная.

Материал: набор из 6 фигур – пять кругов (синие: большой и два малень­ких, зеленые: большой и маленький), маленький красный квадрат.

Методика проведения. Воспитатель раскладывает перед ребенком фигуры в беспорядке и просит определить, какая из фигур в этом наборе лишняя (квад­рат) и почему (все остальные круги). Потом воспитатель убирает квадрат и про­сит ребенка разделить на группы оставшиеся круги и объяснить, почему он их так разделил (по размеру и по цвету).

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который самостоятельно умеет сравнивать и классифицировать предметы по форме, величине и цвету;

–     средний уровень (1 балл) получает ребенок, который допускает 1-

Продолжение приложения А

 

2 ошибки, не вполне уверенно и с помощью взрослого сравнивает и классифици­рует предметы по форме, величине и цвету;

–     низкий уровень (0 балл) получает ребенок, который не умеет сравнивать и классифицировать предметы по форме, величине и цвету даже при помощи взрослого.

Критерий 4. «Пространственные представления»

Задание 1

Цель: выявить понимание пространственных отношений (вверху, внизу, впереди, сзади, слева, справа и так далее).

Форма проведения – индивидуальная.

Материал: не требуется.

Методика проведения. Воспитатель просит ребенка встать на середину групповой комнаты и назвать предметы, которые он видит вверху, внизу, впе­реди, слева, справа от себя по словесному образцу: «Вверху я вижу… . Внизу я вижу… и так далее».

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который правильно без по­мощи взрослого называет нахождение предметов в пространстве по словесному образцу с использованием наречий, обозначающих место;

–     средний уровень (1 балл) получает ребенок, который затрудняется без помощи взрослого назвать нахождение предметов в пространстве по словесному образцу; путает наречия «справа» и «слева»;

–     низкий уровень (0 балл) получает ребенок, который не может назвать нахождение предметов в пространстве по словесному образцу, допускает 3 и бо­лее ошибок.

Задание 2

Цель: определить умение ориентироваться на листе бумаги.

Форма проведения – индивидуальная.

Продолжение приложения А

 

Материал: лист бумаги формата А, разделенный на 25 квадратов (5 – по вертикали и 5 – по горизонтали), на котором в левом верхнем углу нарисован мяч, в правом нижнем углу – звезда, в правом верхнем углу – треугольник, в левом нижнем углу – квадрат; посредине в квадрате стоит крестик.

Методика проведения. Воспитатель дает ребенку восемь заданий:

1     Покажи, что нарисовано в левом верхнем углу?

2     Покажи, что нарисовано в правом нижнем углу?

3     Покажи, что нарисовано в правом верхнем углу?

4     Скажи, в каком углу нарисован квадрат?

5     Поставь над крестиком точку.

6     Нарисуй слева от крестика кружок.

7     Нарисуй справа от крестика треугольник.

8     Под крестиком проведи волнистую черту.

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который самостоятельно ориентируется на листе бумаги и выполнил все задания верно, без ошибок;

–     средний уровень (1 балл) получает ребенок, который допустил 1-2 ошибки при выполнении восьми заданий;

–     низкий уровень (0 балл) получает ребенок, который допустил 3 и более ошибок при выполнении восьми заданий.

Задание 3

Цель: выявить умение передвигаться в пространстве, ориентируясь на план-схему.

Форма проведения – индивидуальная.

Материал: план-схема групповой комнаты, предварительно нарисованная воспитателем, на котором изображены 5-6 предметов реальных (находящихся в данный момент в этой комнате) мебели (вид сверху) – столы – в виде кругов, шкафы – в виде прямоугольников, стулья – квадраты и так далее. На этом плане

Продолжение приложения А

 

стрелками изображен путь движения, который должен пройти ребенок, чтобы найти спрятанную игрушку. Место ее расположения обозначено на плане кре­стиком. Обязательное правило: нужно по порядку пройти весь путь. Нельзя сразу направиться к тому месту, где спрятана игрушка.

Методика проведения. Воспитатель просит ребенка внимательно рассмот­реть план движения и, передвигаясь по стрелкам, которые указывают нужное направления комментировать свои действия словесно. Например, ребенок дол­жен говорить: «Сначала от этого стола я пройду прямо до стула, который стоит посредине комнаты. Оттуда поверну направо и дойду до стола, потом поверну налево и так далее».

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который самостоятельно и правильно умеет передвигаться в пространстве, ориентируясь на план-схему, по­стоянно комментирует свои передвижения;

–     средний уровень (1 балл) получает ребенок, у которого не получается передвигаться в пространстве по плану-схеме без дополнительной помощи взрослого и который затрудняется выражать словесно направление своих пере­движений;

–     низкий уровень (0 балл) получает ребенок, который не умеет передви­гаться в пространстве, ориентируясь на план-схему, и не может рассказать о своих передвижениях даже при помощи взрослого.

Критерий 5. «Временные представления»

Задание 1

Цель: выявить знание названий частей суток, их последовательности и умение определить часть суток по деятельности человека.

Форма проведения – индивидуальная.

Материал: картинки с изображением человека (ребенка) спящего в тем­ноте, делающего зарядку, спящего при дневном свете, смотрящего вечернюю пе-­

Продолжение приложения А

 

редачу.

Методика проведения. Педагог дает ребенку инструкцию: «Посмотри на картинки. В какое время суток это происходит? Разложи их по порядку».

Оценивание результатов:

–     высокий уровень (2 балла) получает ребенок, который все карточки раз­ложил правильно, по порядку, ошибок в назывании частей суток нет;

–     средний уровень (1 балл) получает ребенок, у которого последователь­ность карточек правильная, но есть ошибки в назывании частей суток или наобо­рот;

–     низкий уровень (0 балл) получает ребенок, который неправильно разло­жил карточки, части суток не назвал.

Задание 2

Цель: выявить знание названий дней недели и их последовательности.

Форма проведения – индивидуальная.

Материал: карточки со знаками-символами занятий или режимных процес­сов в детском саду, относящихся к тому или иному дню недели.

Методика проведения. Педагог дает ребенку задание и задает вопросы: «Посмотри на эти значки. Каждый значок обозначает занятия, которые проходят у нас в определенные дни недели: краски – рисование; цифры – математика; буквы – обучение грамоте; мяч – физкультура; музыкальные инструменты – му­зыка; две пустых карточки – выходные дни (суббота и воскресенье). Разложи их по порядку с начала до конца недели. Назови, в какой день недели проходит это занятие».

Оценивание результатов:

–     высокий уровень (3 балла) получает ребенок, который последовательно назвал все дни недели и разложил все карточки-символы занятий в детском саду;

–     средний уровень (2 балла) получает ребенок, который допустил 2-              3 ошибки при определении последовательности дней недели и раскладыванию

Окончание приложения А

 

карточек-символов;

–     низкий уровень (1 балл) получает ребенок, который не смог назвать все дни недели в нужной последовательности и допустил 4-5 ошибок при расклады­вании карточек-символов.

Задание 3

Цель: выявить умения определять время по часам и выставлять нужное время на часах.

Форма проведения – индивидуальная.

Материал: модель циферблата часов.

Методика проведения. Педагог кладет перед ребенком часы и просит по­смотреть на них внимательно. Задает ребенку вопросы и дает задания: – Скажи, который час показываю часы? Что ты делаешь в 9 утра, например, в детском саду? – Поставь стрелки часов так, чтобы на них было 4 часа. Что ты делаешь в детском саду или дома в 4 часа дня?

Оценивание результатов:

–     высокий уровень (3 балла) получает ребенок, который по часам пра­вильно определил, который час и поставил время, которое требуется; правильно ответил на все вопросы педагога;

–     средний уровень (2 балла) получает ребенок, который по часам пра­вильно определил, который час, но не смог поставить время, которое требуется или наоборот; на вопросы педагога отвечал неуверенно, пользовался помощью взрослого;

–     низкий уровень (1 балл) получает ребенок, который по часам непра­вильно определил, который час, и не смог поставить время, которое требуется; затруднялся отвечать на вопросы, отвечал неправильно, не смог воспользоваться помощью взрослого.

ПРИЛОЖЕНИЕ Б

(справочное)

 

Результаты диагностики начального уровня сформированности математических представлений у детей старшего дошкольного возраста

 

Таблица Б – Протокол 1. Результаты диагностики начального уровня сформированности математических представлений у детей старшего дошкольного возраста

 

Ребенок	Критерии																									Сумма баллов	Уровень
	количественные представления и счет					величина и ее измерение					геометрические фигуры					пространствен­ные представления					временные представления
	задание 1	задание 2	задание 3	сумма баллов	уровень	задание 1	задание 2	задание 3	сумма баллов	уровень	задание 1	задание 2	задание 3	сумма баллов	уровень	задание 1	задание 2	задание 3	сумма баллов	уровень	задание 1	задание 2	задание 3	сумма баллов	уровень
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
Ребенок 1	1	1	2	4	С	2	0	1	3	С	1	1	1	3	С	1	2	1	4	С	1	0	0	1	Н	15	С
Ребенок 2	2	2	1	5	В	2	2	2	6	В	1	2	2	5	В	2	1	1	4	С	2	1	2	5	В	25	В
Ребенок 3	1	2	0	3	С	1	1	1	3	С	1	2	0	3	С	1	0	1	2	С	0	1	2	2	Н	14	С
Ребенок 4	0	1	0	1	Н	0	0	0	0	Н	1	1	0	2	С	0	1	0	1	Н	0	0	0	0	Н	4	Н
Ребенок 5	1	2	1	4	В	1	1	0	2	С	1	1	1	3	С	1	0	1	2	С	1	1	2	4	С	15	С
Ребенок 6	2	2	2	6	В	1	2	2	5	В	1	1	2	4	С	2	1	2	5	В	1	2	1	4	С	24	В
Ребенок 7	2	1	1	4	С	2	1	1	4	С	1	1	0	2	С	1	1	0	2	С	1	1	0	2	С	14	С
Ребенок 8	1	1	0	2	Н	0	1	0	1	Н	1	1	1	3	С	0	0	0	0	Н	0	0	1	1	С	7	Н
Окончание приложения Б
Окончание таблицы Б
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
Ребенок 9	1	1	0	2	Н	1	1	1	3	С	1	0	1	2	С	1	2	1	4	С	1	1	2	4	С	15	С
Ребенок 10	2	1	1	4	С	1	0	1	2	С	1	2	1	4	С	1	1	0	2	С	1	1	1	3	С	16	С
Ребенок 11	2	1	1	4	С	0	1	1	2	С	1	2	0	3	С	1	1	1	3	С	1	1	1	3	С	15	С
Ребенок 12	2	1	1	4	С	0	1	1	2	С	1	2	0	3	С	1	1	1	3	С	1	1	1	3	С	15	С
Ребенок 13	1	1	2	4	С	1	1	0	2	С	2	1	1	4	С	1	2	1	3	С	1	1	0	2	С	16	С
Ребенок 14	1	2	0	3	С	1	1	2	4	С	1	1	1	3	С	1	1	0	2	С	2	1	1	4	С	16	С
Ребенок 15	1	1	1	3	С	1	1	1	3	С	1	2	1	4	С	2	1	1	4	С	1	1	1	3	С	17	С
Ребенок 16	2	2	2	6	В	2	2	2	6	В	2	1	2	5	В	2	2	2	6	В	2	2	1	5	В	28	В
Ребенок 17	1	1	2	4	С	1	1	0	2	С	1	2	1	4	С	1	1	1	3	С	1	1	0	2	С	15	С
Ребенок 18	1	0	0	1	Н	1	0	1	2	С	0	0	0	0	Н	0	1	0	1	Н	0	1	0	1	Н	5	Н
Ребенок 19	1	1	1	3	С	1	2	1	4	С	1	0	1	2	С	1	1	1	3	С	1	0	1	2	С	14	С
Ребенок 20	2	2	2	6	В	1	2	1	4	С	2	2	1	5	В	2	1	2	5	В	2	1	2	5	В	25	В

 

Обозначения:

–     В – высокий уровень;

–     С – средний уровень;

–     Н – низкий уровень.

ПРИЛОЖЕНИЕ В

(обязательное)

 

Комплекс логико-математических игр на формирование

математических представлений у детей 5-6 лет

 

1 Логико-математические игры на формирование количественных пред­ставлений и счетной деятельности «Сколько?»

Цель: формировать количественные и счетные представления, развивать умения задавать вопросы и выделять свойства предметов.

Вариант 1

Материал: 8-10 карточек с изображениями предметов.

Ход игры: на доске закрепляется карточки с различным количеством пред­метов.

Ведущий говорит: «Сейчас я загадаю загадку. Тот, кто ее отгадает, пере­считает предметы на карточке и покажет цифру. Слушайте загадку. Сидит де­вица в темнице, а коса на улице». Играющие догадавшиеся, что это морковь, пе­ресчитывают, сколько морковок нарисовано на карточке, и показывают, напри­мер, цифру 4. Кто быстрее поднял цифру, становится ведущим. Вместо загадок можно давать описание предмета. Например: «Это животное ласковое и доброе, оно не разговаривает, но знает свое имя, любит играть с мячом, клубком ниток, пьет молоко и живет вместе с людьми. Кто это? Сосчитайте сколько».

Вариант 2

Материал: логические фигуры – логические блоки Дьенеша.

Ход игры: придумывание вопросов, начинающихся со слова «сколько».

Описание игры: Дети делятся на две команды. Воспитатель раскладывает логические фигуры в любом порядке и предлагает детям придумать вопросы, начинающиеся со слов «Сколько...». За каждый правильный вопрос и ответ – фишка. Выигрывает команда, набравшая большее количество фишек.

Варианты вопросов: «Сколько больших фигур?» «Сколько красных фигур

Продолжение приложения В

 

в первом ряду?» (по горизонтали), «Сколько кругов?» и так далее.

«Найди пару»

Цель: формировать количественные и счетные представления, умение со­относить количество и число.

Вариант 1

Материалы: карточки с цифрами от 3 до 10 и карточки с изображением разного количества однородных предметов.

Ход игры: на подносе изображением вниз лежат карточки с цифрами от 3 до 10 (по одной на каждого игрока). На столе изображением вверх лежат число­вые карточки и с изображением разного количества однородных предметов. По сигналу играющие берут по одной карточке с цифрой, проходят вдоль стола, находят «свою пару», то есть отыскивают числовые карточки и картинки, соот­ветствующие цифре на своей карточке, и направляются в «домик» (место на ковре, «очерченное» толстым шнуром).

Вариант 2

Цель: закрепить умение соотносить цифру с количеством.

Материалы: цифры и карточки с таким же количеством точек.

Ход игры: дети по желанию делятся на две команды. У каждой свой стол, на одном столе в беспорядке лежат перевернутые цифры, на другом – карточки с таким же количеством точек. Дети бегают по комнате. По сигналу берут кар­точки со столов и отыскивают свою пару, то есть к каждой карточке подбирают цифру, соответствующую количеству точек на карточке.

«Бьют часы»

Цели: упражнять в правильном составлении последовательности чисел; учить сопоставлять количество предметов с числом, закреплять навыки и пра­вила счета; развивать внимание, быстроту реакции на сигнал, зрительную ори­ентировку при нахождении цифр.

Материалы: часы, нарисованные на большом листе бумаги, силуэты цифр,

Продолжение приложения В

 

маленькие фигурки (по количеству цифр на циферблате).

Ход игры: попав на бал, Золушка забывает о времени, так как часы закол­дованы и вместо цифр на них нарисованы предметы. Фея просит расколдовать часы, посчитав количество предметов на каждом делении часов и поставив нуж­ную цифру.

Стрелки спешат, стоять не велят,

Предметы считай, цифры вставляй.

Дети бегут по кругу, на сигнал быстро останавливаются.

Названный ребенок считает предметы возле того деления, напротив кото­рого остановился, соблюдая правила счета, ищет за кругом нужную цифру и накладывает ее на предметы.

 Игра заканчивается, когда все цифры будут стоять на своих местах. Счет до 12.

Правила: напомнить детям правила счета хаотично расположенных пред­метов. Научить быстро осуществлять остановку на сигнал, проверять последова­тельность расположения цифр посредством счета.

«Домино»

Цель: развивать счетные умения, внимание.

Ход игры: детям раздают по 6 карточек домино, предлагают назвать цифры и количество предметов на карточках. Первый ребенок делает ход и называет, какие у него предметы, сколько их и какая изображена цифра.

Следующий ребенок кладет такую же цифру и называет ее. Выигрывает тот, у кого быстрее закончатся карточки.

«Математическое лото»

Цель: формировать у детей количественные представления, умение счи­тать, развивать представления о цифрах.

Ход игры: каждому ребенку раздают карточку, разделенную на 6 частей с разным количеством предметов. Детям показывают разрезанные карточки и

Продолжение приложения В

 

предлагают найти на своем листе такое же количество предметов.

Уточняем, почему ребенок выбрал именно эту карточку. Выигрывает тот, кто раньше всех заполнил свою карточку.

«Веселый счет»

Цель: учить прямому и обратному порядковому счету в пределах десяти.

Материалы: карточки с изображением животных – 10 штук, карточка с изображением парусника – 1 штука.

Ход игры: воспитатель читает рассказ «Веселый счет», где козленок пооче­редно считает животных. Вместе с детьми помочь козленку посчитать животных, показывая их картинки. Определить цель счета (для чего считал козленок живот­ных). Помочь животным сойти на берег (упражнять детей в обратном счете).

Домино «Веселая зарядка»

Цель: учить прямому, обратному, смешанному (вразнобой) счету в преде­лах десяти. Развивать внимание, логическое мышление.

Материал: карточки-фишки.

Ход игры: так же, как и в игре «Домино». Только вместо цифр – картинки. Дети находят соответствующую картинку и таким образом игра продолжается.

Домино «Белоснежка и семь гномов»

Цель: учить прямому, обратному, смешанному (вразнобой) счету в преде­лах десяти. Развивать внимание, логическое мышление.

Материал: карточки-фишки.

Ход игры: так же, как и в игре «Домино». Только вместо цифр – картинки. Дети находят соответствующую картинку и таким образом игра продолжается.

«Мои первые цифры»

Цель: учить количественному счету до 10.

Материал: карточки – цифры – 10 штук, карточки – животные –10 штук.

Ход игры: воспитатель раздает карточки с цифрами детям (5-6 человек), карточки с животными лежат на столе. Тот, кто быстрее подберет к карточкам

Продолжение приложения В

 

цифрам, карточки с разным количеством животных в соответствии с заданной цифрой, тот и выиграл.

2 Логико-математические игры на формирование представлений о величи­нах и способах их измерения

«Построй лестницу»

Цель: формировать у детей представление о величинах.

Материал: палочки Кюизенера.

Ход игры: детям предлагалось выстроить из брусочков сначала большую лестницу для великана, потом – маленькую для гнома, сосчитать, сколько пало­чек в каждой из этих лестниц, найти самую длинную и самую короткую палочку, назвать их цвет. Аналогично ребенок может построить домик, кроватки, столы, стулья разных размеров.

«Состав восьмерки»

Цель: формировать у детей представление о величинах и способах их из­мерения.

Материал: палочки Кюизенера.

Ход игры: игра проводилась, когда дети уже были знакомы с составом чи­сел от 2 до 7, умели присчитывать по одному, по два, по три.

Методика проведения игры: воспитатель кладет перед ребенком палочку-восьмерку и просит ребенка выложить по всей ее длине палочки-единички и со­считать, сколько их получилось. Ребенок делает вывод о том, что в одной длин­ной палочке содержится восемь маленьких. Потом ребенку предлагается соста­вить восьмерку из других палочек, используя комбинации из двух, трех и четы­рех палочек, например, 4 и 4, 1 и 7, 5 и 3; 2, 2 и 4, 1 и 2 и 3 и 2 и так далее. Каждый раз ребенок делает вывод о том, сколько и каких палочек включает в себя па­лочка-восьмерка. Эта игра подготавливает ребенка к арифметическим действиям сложения.

Продолжение приложения В

 

«Коричневая лестница»

Цель: формировать у детей представление о величинах и способах их из­мерения.

Материал: логические блоки Дьенеша.

Ход игры: десять деревянных призм с квадратным основанием (длина каж­дой 20 см); размер бокового ребра каждой призмы уменьшается от 10 до 1 см. Детям дается задание – построить лестницу. В ходе игры призмы прикладыва­ются друг к другу в определенной последовательности – от самой толстой к са­мой тонкой так, чтобы толщина каждой последующей была на 1 см меньше предыдущей. В результате получается лестница, равномерность ступенек кото­рой можно легко увидеть или ощутить руками. В этой игре используется алго­ритм построения упорядоченного, сериационного ряда.

«Измерим ленту»

Цель: учить измерять длину предмета с помощью условной мерки.

Материалы: лента (60 см), мерка – полоска (20 см), счетные палочки.

Ход игры: на доске горизонтально прикреплена лента.

Воспитатель. Посмотрите, какая красивая лента на доске. Из нее мы сде­лаем бантики вот такой длины (показываю мерку). Интересно, сколько бантиков получится? Как узнать?

Инструкция по измерению:

–     начать измерять от самого края;

–     отметить конец мерки;

–     после того как мерка уложится полностью, положить палочку (чтобы не

–     запутаться);

–     перенести мерку и продолжить измерение.

–     Сколько бантиков получиться? Как узнать? (Пересчитать палочки).

«Весовые качели»

Цели: развивать умение сравнивать и обобщать; научить ребенка в разных

Продолжение приложения В

 

ситуациях приходить к выводу, что вес продуктов, длина предметов не зависят от их количества; закрепить представления об измерении длины и веса с помо­щью общепринятой меры.

Материалы: плюшевые игрушки (медведь, белочки, тигры), мольберт, ка­рандаши.

Ход игры: смотритель зоопарка (воспитатель) просит детей помочь ему взвесить двух медвежат; так как те очень любят качаться на качелях, смотритель придумал, как их развлечь, а заодно и измерить вес. На одну сторону качелей он сажает медведя, а на другой просит расположить других животных, пока качели не уравновесятся. Дети делятся на команду белочек и команду тигров. По сиг­налу команда белочек большими прыжками в длину поочередно будет сажать на качели белочек, а команда тигров бегом на четвереньках – тигрят.

Игра закончится, когда качели будут в горизонтальном положении, то есть уравновесятся.

Вопросы:

–     Как мы измеряли медведей? (Уравновешивали качели).

–     Сколько весит медведь в белочках? (5).

–     Сколько в тиграх? (3).

–     Чей вес больше – медведя в белочках или медведя в тиграх, ведь 3 тигра

–     меньше, чем пять белочек? Можно ли ответить на этот вопрос? Почему? (Разные мерки).

–     Что же лучше делать – пересчитывать вес в предметах или измерять?

–     Какой должна быть мерка, чтобы сравнить вес двух предметов? (Одина­ковой).

Дети измеряют вес медведей только в белочках или только в тиграх, срав­нивают, чей вес больше, и ставят знаки «больше», «меньше».

Педагог приводит детей к выводу, что вес предметов лучше измерять на весах, чем пересчитывать.

Продолжение приложения В

 

«Как измерить пшено в кастрюльках?» (с подгруппой 5 человек)

Цель: формировать у детей умение определять объем с помощью мерок

Материал: две баночки с пшеном (баночки разной формы). Разные пред­меты: квадраты, палочки, линейка, стаканчик, коробочка и так далее.

Ход игры: в двух баночках разной формы насыпано пшено, рядом на столе находятся различные предметы (квадраты, палочки, линейка, стаканчик, коро­бочка и так далее).

Вопросы к детям:

–     Скажите, в какой баночке пшена больше?

–     Что нужно сделать, чтобы это узнать?

–     Что может быть мерой для пшена?

–     Пшено можно палочкой измерить?

–     Не получается!

–     Можно ли измерить квадратиком? Яша пытается измерить квадратиком.

–     Нет, не получается, что же делать?

–     Как же нам измерить?

–     А я попробую кружечкой

–     Сколько мерок пшена в этой баночке?

–     Что у нас было меркой?

–     Как вы узнали, что пшена поровну?

В результате обсуждения педагог подводит детей к правильной технике отмеривания: наполнять мерку надо «по край».

«В каком стакане больше гороха?»

Цель: сформировать понятие о сохранении дискретных количеств.

Материал: пластмассовая баночка с горохом и два одинаковых прозрачных стаканчика.

Ход игры: перед ребенком стоят: пластмассовая баночка с горохом и два одинаковых прозрачных стаканчика. Предлагаю ребенку взять в каждую руку по

Продолжение приложения В

 

горошине и одновременно опускать их в прозрачные стаканчики.

После того как часть стаканчиков заполнится горохом ребенок прекращает работу.

Воспитатель спрашивает:

–     Скажи, в каком стаканчике горошин больше?

–     Поровну, я в каждую руку брала по одной горошинке и складывала их по стаканчикам, а стаканчики одинаковые. Далее воспитатель пересыпает горо­шины из одного стаканчика в другой, узкий и высокий.

–     Где горошин больше?

–     В этом стакане и в этом горошин одинаково, потому что не одну горо­шину не убирали и не прибавляли.

–     А почему здесь так высоко горошинки поднялись?

–     Он узенький и высокий, а этот стаканчик низкий и широкий, а горошин одинаково, потому что не брали горошины и не прибавляли».

3 Логико-математические игры на формирование представлений о геомет­рических фигурах

«Чей домик?»

Цель: формирование представлений о геометрических формах и умения их сравнивать.

Материал: картинки с изображением героев мультфильма; пять домиков разной формы и величины.

Ход игры: воспитатель сообщает игровые правила: «Надо всех героев раз­местить по домикам. Кто больше всех? Кто меньше всех? Что ты можешь сказать про слоненка? Поместится ли слоненок в дом попугая? А поместится ли попугай в домик обезьянки? ...»). Как вы думаете, кто и в каком домике живет слоненок, мартышка, обезьянка, попугай, удав? (На магнитики в домики прикрепляются герои мультфильма). У удава – широкий и низкий, у мартышки – прямоуголь­ный, но выше, чем у попугая; у попугая – узкий, но ниже, чем у мартышки; у

Продолжение приложения В

 

слона высокий квадратный; у мартышки – прямоугольник высокий; попугай – узкий, но низкий, удав – длинный, но узкий. Дома героев мультфильма – это гео­метрические фигуры. Назовите их.

«Почини ковер-самолет»

Цели: учить находить одинаковые геометрические формы, устанавливая между ними равенство.

Материалы: гимнастический коврик с отверстиями в виде геометрических фигур, геометрические фигуры.

Ход игры: гном дарит детям ковер-самолет, но для того, чтобы он полетел, необходимо залатать в нем «дыры», имеющие форму геометрических фигур, найдя и соединив две одинаковые по форме, цвету и размеру геометрические фи­гуры необычным способом (разными частями тела.)

Вопросы: назовите формы, которые вы соединили. Почему они равны?

Далее гном просит детей посчитать все геометрические фигуры заплатки на ковре:

–     Сколько здесь квадратов? (6)

–     А прямоугольников? (11).

–     Сколько кругов? (5).

–     Сколько треугольников? (7).

«Магазин»

Цель: формировать представления о форме предметов, умение сравнивать, считать до 5; развивать умения выявлять и абстрагировать свойства, умения рас­суждать, аргументировать свой выбор.

Материалы: товар (карточки с изображением предметов – логические блоки Дьенеша).

Ход игры: дети приходят в магазин, где представлен большой выбор игру­шек. У каждого ребенка 5 логических фигур – «денежек». На одну «денежку» можно купить только одну игрушку. Правила покупки: купить можно только та­-

Продолжение приложения В

 

кую игрушку, в которой есть хотя бы одно свойство логической фигуры «де­нежки», которая есть у ребенка. Правило можно усложнить выбор игрушки по двум свойствам (например, большой квадрат, синий квадрат и так далее).

«Какой фигуры не хватает?»

Цель: формировать представления о форме предметов, умения сравнивать, классифицировать геометрические фигуры по форме, выявлять и абстрагировать свойства, умения рассуждать, аргументировать свой выбор.

Материалы: карточка с недостающей фигурой (знак вопроса), в правой ча­сти которой нарисованы 6 фигур, из которых нужно выбрать недостающую фи­гуру (пример на рисунке В1).

 

 

Рисунок В1 – Какой фигуры не хватает

 

Ход игры: из 9 фигур, изображенных, нужно выбрать ту, которую надо по­местить на место недостающей в третьем ряду. Поиск фигуры осуществляется на основе анализа рядов фигур по горизонтали или вертикали. В рядах фигур скрыты 3 закономерности: количество прямых линий; положение прямоуголь­ника; форма фигуры внутри прямоугольника.

Продолжение приложения В

 

«Непересекающиеся множества»

Цель: формировать представления о форме предметов, умения сравнивать, классифицировать геометрические фигуры по форме, величине и цвету.

Оборудование: программно-аппаратный комплекс «Колибри» или интер­активная доска.

Ход игры: детям предлагается: в красный круг собрать все красные фи­гуры; в желтый – все желтые (рисунок В2). После выполнения практической части проводится беседа с детьми по следующим вопросам (рисунок В3):

–     Какие фигуры лежат в желтом круге? (Все желтые).

–     Какие в красном круге? (Все красные).

–     Почему у вас оказались фигуры, которые не попали ни в один

круг? (Они не желтые и не красные).

 

 

Рисунок В2-3 – Непересекающиеся множества

Продолжение приложения В

 

«Пересекающиеся множества»

Цель: формировать представления о форме предметов, умения сравнивать, классифицировать геометрические фигуры по форме, величине и цвету.

Оборудование: программно-аппаратный комплекс «Колибри» или интер­активная доска.

Вариант 1

Ход игры: детям предлагается разложить фигуры следующим образом: в красный круг собрать все красные фигуры, а в желтый круг поместить все тре­угольники. Красные треугольники должны попасть в пересечение кругов, так как эти фигуры обладают сразу двумя свойствами: они и красные, и треугольные (рисунок В4).

После выполнения практической задачи проводится беседа по следующим вопросам (рисунок В5):

 Какие фигуры в красном круге? Какие фигуры в желтом круге? Почему есть фигуры, которые попала в пересечение кругов? Почему есть фигуры, кото­рые лежат вне кругов? (Они не красные и не треугольные).

Аналогично можно выполнять классификацию по цвету и размеру, по форме и размеру.

«Три кольца»

Цель: формировать представления о форме предметов, умения сравнивать, классифицировать геометрические фигуры по форме, величине и цвету.

Оборудование: программно-аппаратный комплекс «Колибри» или интер­активная доска.

Ход игры: детям предлагается выполнить классификацию следующим об­разом: в желтое кольцо собрать все треугольники, в красное – все красные фи­гуры, а в зеленое – все маленькие фигуры. После выполнения практической за­дачи дети отвечают на вопросы:

–     Какие фигуры в желтом кольце? (Все треугольники).

Продолжение приложения В

 

–     Какие фигуры в красном кольце? (Все красные).

–     Какие фигуры в зеленом кольце? (Все маленькие).

–     Какие фигуры лежит внутри желтого, красного и зеленого колец? (Крас­ный маленький треугольник.)

–     Какие фигуры лежат внутри желтого и зеленого колец, но вне красного? (Маленький зеленый треугольник, (маленькие треугольные, но не красные).

–     Какие фигуры лежат внутри желтого и красного колец, но вне зеленого? (Большой красный треугольник. Красные, треугольные, но не маленькие).

–     Какие фигуры лежат внутри красного и зеленого колец, но вне желтого? (Красный, маленький круг (красные, маленькие, но не треугольные).

–     Какие фигуры лежат вне желтого, красного и зеленого колец? (Не крас­ные, не треугольные и немаленькие).

 

 

Рисунок В4 – Пересекающиеся множества

Продолжение приложения В

 

 

Рисунок В5 – Пересекающиеся множества

 

«Три обруча»

Цель: формировать представления о форме предметов, умения сравнивать, классифицировать геометрические фигуры по форме, величине и цвету.

Оборудование: программно-аппаратный комплекс «Колибри» или интер­активная доска.

Ход игры: детям предлагается разместить в красном обруче все треуголь­ники и круги, в зеленый обруч поместить все зеленые фигуры, а в желтый все геометрические фигуры, у которых есть углы.

После выполнения практической задачи дети отвечают на вопросы (рису­нок В6):

Какие фигуры в желтом обруче? (Все геометрические фигуры с углами).

Какие фигуры в красном обруче? (Все треугольники и круги).

Какие фигуры в зеленом обруче? (Все зеленые фигуры).

Какие фигуры лежит внутри желтого, красного и зеленого обруча? (Зеле­ный треугольник).

Продолжение приложения В

 

Какие фигуры лежат внутри желтого и зеленого обруча, но вне красного? (Зеленые фигуры, имеющие углы).

Какие фигуры лежат внутри желтого и красного обруча, но вне зеленого? (Все треугольники, но не зеленые).

Какие фигуры лежат внутри красного и зеленого обруча, но вне желтого? (Зеленый круг).

Какие фигуры лежат вне желтого, красного и зеленого обруча? (Все овалы, но не зеленые).

 

 

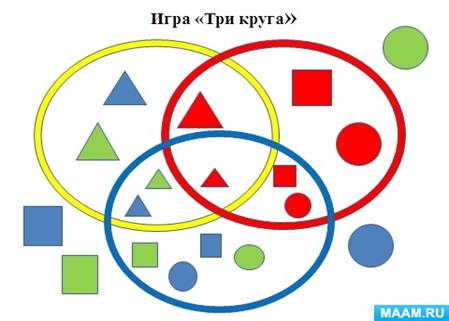
Рисунок В6 – Три обруча

 

4 Логико-математические игры на формирование пространственных представлений

«Рисуем фигуры»

Цель: формирование умения ориентироваться на листе бумаги.

Материалы: листы бумаги и карандаши на каждого ребенка.

Ход игры: воспитатель предлагает детям отгадать, какая фигура нарисо­-

Продолжение приложения В

 

вана на листе бумаги, лежащем в конверте. Для этого дети должны правильно выполнить задание по словесной инструкции: «От точки слева направо прове­дите линию длиной в три клетки, затем сверху вниз проведите еще одну линию длиной в три клетки, потом проведите справа налево 3 клетки и, наконец, снизу вверх 3 клетки».

– Какая фигура получилась? (воспитатель показывает карточку с изобра­жением квадрата).

За это задание вы получаете от Незнайки букву «С».

«Геометрический диктант»

Цель: формирование умения ориентироваться на листе бумаги.

Материалы: перед детьми лежит лист бумаги и набор геометрических фи­гур.

Ход игры: воспитатель дает инструкции, а дети должны выполнять в быст­ром темпе:

Нарисуйте в прямоугольнике:

–     в правом верхнем углу – квадрат;

–     в левом нижнем углу – шарик;

–     в правом нижнем углу – треугольник;

–     в левом верхнем углу – круг;

–     в середине –овал.

Воспитатель:

–     Где нарисовали шарик? (В левом нижнем углу).

–     Где нарисовали квадрат? (В правом верхнем углу).

–     Где нарисовали овал? (В середине прямоугольника).

После выполнения задания дети могут проверить правильность выполне­ния: у воспитателя заготовлен заранее лист с нарисованными геометрическими фигурами соответственно диктанту.

Продолжение приложения В

 

«Я еду на машине»

Цель: закрепление умения ориентироваться на листе бумаги.

Материалы: перед каждым ребенком лист бумаги (А3) и маленькая ма­шинка.

Ход игры: дети, слушая инструкции воспитателя, передвигают машинку в нужном направлении.

Например, в правом нижнем углу листа – гараж, оттуда мы поедем по ниж­ней стороне листа в школу. Она находится в левом нижнем углу, а после школы мы поедем в зоопарк, который находится в правом верхнем углу, и так далее.

«Синхронное плавание»

Цель: формировать умение передвигаться в пространстве, ориентируясь на словесную инструкцию.

Ход игры: дети стоят на ковре на одинаковом расстоянии друг от друга.

Воспитатель дает инструкции по передвижению в пространстве одновре­менно всем детям, иногда изменяя их направление относительно друг друга. Например, все сделали шаг вперед, шаг вправо, два шага влево, повернулись вправо, сделали шаг назад и так далее.

«Новая походка»

Эту игру можно проводить с 2-3 детьми на прогулке.

Ход игры: воспитатель говорит детям, что сейчас они будут ходить так, как она скажет – сначала по прямой линии, а потом изменяя движение в разные сто­роны. Дает детям команды: два шага вперед, один шаг вправо, или шаг назад, два шага вперед. При усложнении игры ребенок должен не только контролировать свою «походку», но и повернуть корпус так, чтобы прийти к определенной цели.

«Преодолей лабиринт и проведи друзей»

Цели: развивать пространственную ориентировку; закреплять умение практически дифференцировать пространственные отношения в различных за­даниях, понимать направление движения по план-схеме.

Продолжение приложения В

 

Материалы: карточки с цифрами, карточки с точками, обручи, скакалки, куб, вырезанные из картона круги.

Ход игры: дети строятся в одну или две колонны (в зависимости от наличия оборудования и места проведения). Педагог сообщает, что им надо преодолеть препятствия, которые встречаются на их пути, чтобы добраться до форта, пока­зывает им карту, по которой дети будут двигаться, соблюдая направление дви­жения. Но для того, чтобы быстро пройти лабиринт, надо расставить точки с цифрами последовательно, согласно карте (их расставляет капитан, дети помо­гают ему советами). На них они будут ориентироваться, а капитан группы дол­жен запомнить двигательные упражнения:

–     обежать озеро (большой обруч) с правой стороны;

–     выполнить прыжки правым боком через маленькие ручейки

–     (скакалки);

–     проползти тоннель;

–     обежать слева гору (конус);

–     перейти болото, прыгая по кочкам с правой стороны (круг);

–     обежать могучий дуб с левой стороны (куб).

Воспитатель определяет время по песочным часам, если дети уложились в 3 минуты, вручает им второй золотой ключ.

Правила: напомнить детям, что выполнять любое движение необходимо за капитаном по расставленным цифрам, соблюдая направление (справа или слева) согласно плану, не ошибаться, не задерживать друзей.

Если при движении дети ошиблись в направлении, то задание выполняется вновь, при этом теряется время.

5 Логико-математические игры на формирование временных представле­ний

«Что бывает только днем»

Оборудование: 9 картинок с изображениями состояния природы – по три

Продолжение приложения В

 

картинки на каждую часть суток (утро, день, вечер и ночь):

–     первая картинка – положение солнца на горизонте;

–     вторая картинка – тень от предметов;

–     третья картинка цветы днем – полностью раскрыли свои лепестки;

–     вечером – лепестки начинают складываться; ночью – лепестки закрыты.

Дети играют парами.

Ход игры: картинки разложены перед детьми. Дети должны выбрать из них только те, на которых изображено состояние природы днем. Дети показывают отобранные картинки и рассказывают, что на них изображено, и почему они счи­тают, что это бывает только днем. Выигрывают те пары детей, которые без оши­бок выполнили задание.

«Помощник Будильник»

Материалы: самодельные будильники с цветными кружками и движу­щейся стрелкой (на циферблате кружки обозначают: красный – утро, желтый – день, фиолетовый – вечер, черный – ночь).

Ход игры: педагог читает загадку, про часть суток, а дети угадывают часть суток и на будильнике поворачивают стрелочку на кружок. Тот, кто допустил ошибку, выбывает из игры, становится рядом с ведущим и становится таким же наблюдателем за остальными, как и ведущий. Победителем становится послед­ний оставшийся в игре, тот, кто не допустил ни одной ошибки.

Загадки

1 Солнце яркое встает,

Петушок в саду поет,

Наши дети просыпаются,

В детский садик собираются. (Утро).

2 Солнце в небе

Ярко светит

На прогулку мы идем,

Продолжение приложения В

 

Песни весело поем. (День).

3 Солнышко лучистое

Село за дома,

Мы пришли с прогулки

Ужинать пора. (Вечер).

4 В небе звездочки горят,

В речке струйки говорят,

К нам в окно луна глядит,

Нашим деткам спать велит. (Ночь).

«Четыре принцессы» – модель частей суток

Материалы: картинки с изображениями принцесс.

Ход игры

Педагог. Сегодня у нас необыкновенные гости. Это четыре принцессы – принцессы безграничной, мистической страны, страны, которой нет на карте, ко­торую нельзя увидеть, но в которой мы все живем. Это страна Времени. Вот эти принцессы (показывает на лица принцесс, которые видны из окон макета замка). А как их зовут, вы сейчас попробуете отгадать. Я прочитаю вам отрывки стихо­творений, а вы ответьте на вопрос: в какое время суток это происходит? Ответ и будет именем.

Медвежонок сонный вышел

И застыл на задних лапах.

И увидел, и услышал,

И учуял теплый запах.

Солнце – ближе, ближе, ближе

Пробирается по чаще,

И все чаще,

И все громче,

Голоса в сосновой чаще. (Л. Мезинов).

Педагог. Ребята, о чем говорится в стихотворении? Правильно, об утре. Так

Продолжение приложения В

 

как зовут первую принцессу? (Вывешивает картинку на доску).

–     Это Утро. В каком она платье и какого цвета у нее волосы? В красном и волосы красного цвета. Почему именно в красном? Потому что утром солнце яр­кое, красное.

–     Теперь отгадайте загадку: вечером умирает, а утром оживает. (День). Как зовут вторую принцессу? День. Какое у нее платье и волосы? Желтые, по­тому что днем самое яркое солнце.

Отгадайте, как зовут третью принцессу

Небо стало розоватым –

Солнце клонится к закату,

Сумрак саду лег на плечи –

Значит, наступает … . (Вечер).

– Вечер. Так зовут третью принцессу. Она в фиолетовом платье.

Осталась последняя принцесса. Вот загадка про нее:

Махнула птица крылом,

Закрыла весь свет одним пером. (Ночь).

– Ночь, эта принцесса в черном платье.

– Принцессы выходит к людям в строгом порядке. Сначала – утро, затем – день, за ней – вечер, а самой последней выходит ночь. Так как у нас на доске (пример картинки на рисунке В7).

 

 

Рисунок В7 – Четыре принцессы: Утро День Вечер Ночь

Продолжение приложения В

 

– Ребята, а как вы узнаете, что на улице утро, день, вечер, ночь.

Расскажите об этом. Дети рассказывают о признаках, по которым они опре­деляют части суток.

«Что перепутал художник?»

Педагог предлагает детям внимательно рассмотреть картинку и найти в ней ошибки в изображении частей суток.

«Радужное лото»

Материалы: конверты с картинками, на которых изображены разные виды деятельности детей в детском саду в разные дни недели (по количеству команд детей); карточки лото с 7 квадратами, раскрашенными в цвета радуги.

Дети играют командами – по 4-5 человек.

Ход игры

Педагог. Я вам предлагаю выполнить задание, которой прислал нам при­дворный звездочет. Давайте вскроем конверты у вас на столах и посмотрим, что там. Ребята, да это же наши занятия. Звездочет хочет, чтобы мы разложили цвет­ные кружочки на карте лото так, чтобы каждый цвет, обозначающий день недели расположился под значком занятия, которое проходит в этот день. Попробуйте все сделать самостоятельно. Вы уже заметили, что дней недели семь и все они идут по порядку. Поэтому звездочет использовал для их обозначения цвета ра­дуги, которых тоже семь и которые тоже идут строго по порядку. Если вы все сделали правильно, то на ваших карточках должна появиться радуга. Заметьте, что этажи у нашего замка тоже радужные. Сравните свою работу и работу прин­цесс.

«Живая неделька»

Ход игры: семь детей построились и пересчитались по порядку.

Первый ребенок слева делает шаг вперед и говорит: «Я – понедельник. Ка­кой день следующий?». Выходит второй ребенок и говорит: «Я – вторник. Какой день следующий?» и так далее. Остальные дети дают задания «дням недели»,

Продолжение приложения В

 

загадывают загадки. Они могут быть самые разные: например, назови день, ко­торый находится между вторником и четвергом, пятницей и воскресеньем, после четверга, перед понедельником и так далее. Назови все выходные дни недели. Назови дни недели, в которые люди трудятся.

Усложнение игры в том, что играющие могут построиться от любого дня недели, например от вторника, до вторника.

«Что сначала, что потом?»

Материал: карточки с цветами радуги и карточки с цифрами от 1 до 7.

Ход игры: играют 2-4 ребенка. Перед детьми лежат карточки с цифрами от 1 до 7, перевернутые цифрами вниз, символизирующие дни недели; и карточки с цветами радуги, перевернутые цветом вниз. Каждый ребенок по очереди берет карточку с цифрой, затем выбирает наугад карточку с цветом. Так каждый участ­ник должен собрать пары: цифра и цвет.

Каждый цвет радуги соответствует цифре, а каждая цифра символизирует день недели. Тот, кто соберет больше всех правильных пар, становится победи­телем.

«Домик дней»

Материал: домик с тремя окошками, разноцветные полоски, подборка сти­хотворений.

Ход игры: педагог предлагает детям рассмотреть домик и говорит, что это «домик дней».

Задания:

–     Как называется день, который уже прошел? (вчера) Он поселился в ниж­нем окошке (вставляем голубую полоску в нижний кармашек).

–     Как называется день, который у нас сейчас, в настоящий момент? (Сего­дня). Он занял среднее окошко (вставляем синюю полоску).

–     Как называются день, который скоро наступит? (Завтра). Он поселился в верхнем окне (вставляем фиолетовую полоску).

Продолжение приложения В

 

–     Сегодня у нас какой день недели? (Например, понедельник). Завтра ка­кой будет? (Вторник). Вчера какой был? (Воскресенье).

Педагог читает стихотворения о вчера, сегодня и завтра (или о воскресенье, понедельнике и вторнике) и предлагает детям «поселить стихотворение» в соот­ветствующее окно.

«Распорядок дня»

Ход игры: дети играют группами – по 4-5 человек.

Каждому ребенку дается карта «Распорядок дня» и задание – дорисовать стрелки на часах так, чтобы часы показывали то время, когда происходили собы­тия, нарисованные на картинках (рисунок В8).

Каждый ребенок показывает свою карточку и называет время, которое он дорисовал на часах. Педагог и другие дети проверяют.

 

 

Рисунок В8 – Распорядок дня

Продолжение приложения В

 

«Часы»

Оборудование: демонстрационная и индивидуальные (для каждого участ­ника) модели часов с подвижными стрелками.

Ход игры: дети рассматривают цифры на циферблате часов, передвигают стрелки. Педагог демонстрирует передвижение короткой стрелки по цифрам, при этом положение длинной стрелки фиксируется на цифре 12. Дети, глядя на модель, называют время с точностью до часа. По заданию педагога они ставят на индивидуальных циферблатах стрелки так, чтобы те показывали 5, 7, 8 и так да­лее часов.

После того, как дети освоят первоначальную азбуку чтения часов, можно переходить к азбуке чтения минут. С этой целью демонстрируется движение ми­нутной стрелки на циферблате макета.

Затем детям предлагаются задания: поставить на индивидуальной модели такое же время, как на демонстрационной, и определить его; расположить стрелки часов так, чтобы они показывали 7 часов; 11 часов 30 минут и тому по­добное.

Детям также можно предложить решить задачу: Перемена началась ровно в 12 часов и длилась четверть часа. Выразите в минутах, сколько длится пере­мена, и покажите на модели.

«Определи, который час»

Ход игры: педагог просит детей по очереди назвать время, которое они ви­дят на часах (рисунок Б9). Потом дети рассказывают, что они в это время обычно делают в двух вариантах: 12 часов дня и ночи, 6 часов утра и вечера, 2 часа дня и ночи, 9 часов утра и вечера и так далее.

 

 

 

Окончание приложения В

 

 

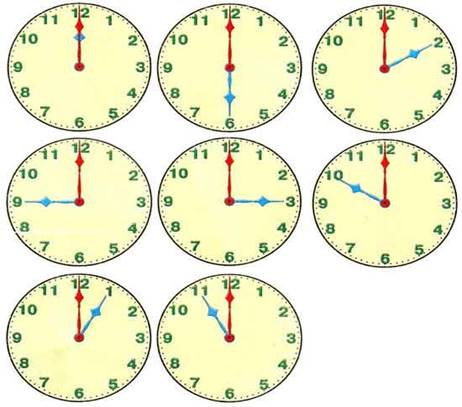
Рисунок В9 – Определи, который час

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ Г

(справочное)

 

Результаты диагностики итогового уровня сформированности математических представлений у детей старшего дошкольного возраста

 

Таблица Г – Протокол 2. Результаты диагностики итогового уровня сформированности математических представлений     у детей старшего дошкольного возраста

 

Ребенок	Критерии																									Сумма баллов	Уровень
	количественные представления и счет					величина и ее измерение					геометрические фигуры					пространствен­ные представления					временные представления
	задание 1	задание 2	задание 3	сумма баллов	уровень	задание 1	задание 2	задание 3	сумма баллов	уровень	задание 1	задание 2	задание 3	сумма баллов	уровень	задание 1	задание 2	задание 3	сумма баллов	уровень	задание 1	задание 2	задание 3	сумма баллов	уровень
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
Ребенок 1	2	1	1	4	С	2	0	1	3	С	2	2	2	6	В	1	2	2	5	В	2	2	0	4	С	22	С
Ребенок 2	2	2	1	5	В	2	2	2	6	В	1	2	2	5	В	2	1	1	4	В	2	1	2	5	В	25	В
Ребенок 3	1	2	1	4	С	1	1	2	4	С	1	2	1	4	С	1	2	1	4	С	2	2	2	6	В	22	С
Ребенок 4	0	0	0	0	Н	1	1	2	4	С	1	1	2	4	С	0	0	0	0	Н	0	0	0	0	Н	8	Н
Ребенок 5	1	2	1	4	В	1	1	2	4	С	1	2	2	5	В	1	2	1	4	С	1	1	2	4	С	20	С
Ребенок 6	2	1	2	5	В	2	2	2	6	В	1	1	2	4	В	2	1	2	5	В	1	2	1	4	В	24	В
Ребенок 7	2	0	2	4	С	2	1	1	4	С	2	0	2	4	С	2	1	2	5	В	1	1	2	4	С	21	С
Ребенок 8	1	1	2	4	С	2	1	1	4	С	1	1	2	4	С	2	2	2	6	В	2	2	2	6	В	24	В
Окончание приложения Г
Окончание таблицы Г
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
Ребенок 9	1	1	2	4	С	1	1	2	4	С	1	2	2	5	В	1	2	1	4	С	1	1	2	4	С	21	С
Ребенок 10	2	1	1	4	С	1	2	1	4	С	1	2	2	5	В	2	1	2	5	В	1	1	2	4	С	22	С
Ребенок 11	2	0	2	4	С	2	1	1	4	С	1	2	1	4	С	2	2	2	6	В	1	1	2	4	С	22	С
Ребенок 12	2	1	1	4	С	2	1	1	4	С	1	2	1	4	С	1	2	1	4	С	1	1	2	4	С	20	С
Ребенок 13	2	2	2	6	В	2	2	2	6	В	2	2	2	6	В	1	2	2	5	В	1	1	2	4	В	27	В
Ребенок 14	1	0	0	1	Н	1	1	2	4	С	0	0	0	0	Н	2	0	2	4	С	2	1	1	4	Н	13	Н
Ребенок 15	1	1	2	4	С	1	1	2	4	С	1	2	1	4	С	2	1	2	5	В	1	1	2	4	С	21	С
Ребенок 16	2	2	2	6	В	2	2	2	6	В	2	1	2	5	В	2	2	2	6	В	2	2	1	5	В	28	В
Ребенок 17	1	1	2	4	С	1	1	2	4	С	1	2	1	4	С	1	1	2	4	С	2	1	2	4	С	22	С
Ребенок 18	1	1	2	4	С	1	2	1	4	С	2	0	2	4	С	2	2	1	5	В	2	1	2	5	В	23	В
Ребенок 19	1	2	1	4	С	1	2	1	4	С	1	2	1	4	С	1	1	2	4	С	1	1	2	4	С	20	С
Ребенок 20	2	2	2	6	В	2	2	2	6	В	2	2	1	5	В	2	1	2	5	В	2	1	2	5	В	27	В

 

Обозначения:

–     В – высокий уровень;

–     С – средний уровень;

–     Н – низкий уровень.

 

Скачано с www.znanio.ru