
ԽԱՉԱՏՈՒՐ ԱԲՈՎՅԱՆԻ ԱՆՎԱՆ ՀԱՅԿԱԿԱՆ ՊԵՏԱԿԱՆ ՄԱՆԿԱՎԱՐԺԱԿԱՆ ՀԱՄԱԼՍԱՐԱՆ

ՖԱԿՈՒԼՏԵՏ__Մաթեմատիկայի, ֆիզիկայի և ինֆորմատիկայի
§ ԲԱԺԻՆ__ֆիզիկա
§ ԿՈՒՐՍ__առաջին
ԱՌԱՐԿԱ— Մագնիսականության դասական տեսություն
ԹԵՄԱ__ Մագնիսական դաշտ
§ ԴԱՍԱԽՈՍ__ Գարիկ Եղիազարյան
§ ՈՒՍԱՆՈՂՈՒՀԻ__Դանիելյան Մարգարիտա
ԵՐԵՎԱՆ 2017թ.
Ներածություն.
Հոսանքն ստեղծում է մագնիսական դաշտ, ուստի՝ կարելի է ենթադրել, որ բնական մագնիսների ստեղծած դաշտերը նույնպես պայմանավորված են որոշակի հոսանքներով: Հիմնվելով Էրստեդի՝ մագնիսական սլաքի վրա հոսանքակիր հաղորդչի ազդեցությունը ցուցադրող փորձերի վրա՝ Ամպերը ենթադրել է, որ Երկրի մագնիսականությունը պայմանավորված է նրա մեջ շրջապտույտ կատարող հոսանքներով: Այնուհետև, ընդհանրացնելով այդ գաղափարը Ամպերն աոաջ է քաշել այն վարկածը, որ ամեն մի մարմնի մագնիսական հատկությունները պայմանավորված է նրա մեջ գոյություն ունեցող տարրական հոսանքներով: Նյութի կաոուցվածքի մասին ժամանակակից պատկերացումները հաստատում են Ամպերի վարկածը: Ատոմի ներսում յուրաքանչյուր էլեկտրոն պտտվելով միջուկի շուրջը, առաջացնում է տարրական շրջանային հոսանք, որն ստեղծում է մագնիսական դաշտ: Մարմնի արդյունարար մագնիսական դաշտը որոշվում է բոլոր այդպիսի տարրական հոսանքների ստեղծած միկրոդաշտերի վերադրմամբ: Եթե տարրական հոսանքների հարթությունները դասավորվում են քաոսային ձեւով, ապա նրանց ստեղծած միկրոդաշտերը միմյանց համակշռում են, եւ մարմինն արդյունարար դաշտ չի ստեղծում:
Արտաքին մագնիսական դաշտում մարմին տեղագրելիս տարրական հոսանքները դասավորվում են որոշակի կարգով, ուստի՝ նրանց միկրոդաշտերի վերադրման հետեւանքով ստեղծված մագնիսական դաշտի ինդուկցիան դառնում է զրոյից տարբեր, նյութը մագնիսանում է:
Արտաքին մագնիսական դաշտում մարմին տեղագրելիս դիտվում են հետեւյալ երեւույթները.
1. Դաշտը մարմնի վրա ազդում է որոշ ուժով կամ մեխանիկական մոմենտով: Անհամասեռ դաշտում մարմինների մի տեսակը (պարամագեւիսակաեւ) տեղափոխվում է դեպի դաշտի լարվածության աճման կողմը, այսինքն ձգվում է դեպի դաշտը: Մարմինների մյուս տեսակը (դիամագնիսական) տեղափոխվում է դեպի դաշտի լարվածության նվազման կողմը, այսինքն վանվում է դաշտից: ձամասեռ դաշտում երկարավուն ձեւ ունեցող մարմինների վրա (ձողերի, սլաքներ) ազդում են 3երկարավուն ձեւ ունեցող մարմինների վրա (ձողերի, սլաքներ) ազդում են մեխանիկական մոմենտներ, որոնք պարամագնիսական մարմիններին կանգնեցնում են դաշտի ուղղությամբ, իսկ դիամագնիսականներիեւ' նրան ուղղահայաց:
2. Դաշտը մագնիսացնում է նյութին, որի հետեւանքով մարմինը ստեղծում է իր սեփական մագնիսական դաշտը, որը վերադրվում է հիմնական (մագնիսացնող) դաշտի վրա: Դիամագնիսական մարմինների համար սեփական դաշտը ուղղված է արտաքին դաշտին հակառակ: Պարամագնիսական մարմինների մոտ սեփական եւ արտաքին դաշտերը ունեն նույն ուղղությունը:Սակայն մագնիսացված մարմնի սեփական մագնիսական դաշտը, ինչպես նրա ներսում, այնպես էլ շրջապատող տարածության մեջ, կախված է ոչ միայն նյութի տեսակից, այլեւ այդ նյութի չափերից եւ ձեւից (գունդ, ձող եւ այլն): Այս պատճառով նյութերի մագնիսական հատկությունները ուսումնասիրելիս ցանկալի է ընտրել այնպիսի մեթոդներ, որոնց մեջ մարմինների ձեւը եւ չափերը հաշվի առնելու անհրաժեշտություն չզգացվի:
Մագնիսական դաշտ
Մագնիսական փոխազդեցությունը կախված չէ հաղորդիչների լիցքերից, այն առաջանում է միայն հաղորդիչներում հոսանքների առկայության դեպքում եւ կախված է այդ հոսանքների մեծությունից: Էլեկտրական հոսանքներն ազդում են մագնիսների վրա, եւ հակառակը, մագնիսներն ազդում են նույն էլեկտրական հոսանքների վրա: Նման ձեւով փոխազդում են եւ երկու հոսանքակիր հաղորդիչներ: Հոսանքների փոխազդեցությունը իրականացվում է մի դաշտի միջոցով, որը կոչվում է մագնիսական: Այս անվանումը առաջացել է այն պատճառով, որ, ինչպես 1820թ. նկատել էր էրստեդը, հոսանքով ստեղծված դաշտը կողմնորոշող ազդեցություն է թողնում մագնիսական սլաքի վրա: Այսպիսով, շարժվող լիցքերը (հոսանքները) փոփոխում են իրենց շրջապատող տարածության հատկությունները' նրա մեջ ստեղծելով մագնիսական դաշտ: Այդ դաշտը դրսեւորվում է այն բանում, որ նրա մեջ շարժվող լիցքերի (հոսանքների) վրա ուժեր են ազդում:
Ինչպես էլեկտրական դաշտը ուսումնասիրելու համար օգտագործեցինք փորձնական կետային լիցք, այնպես էլ մագնիսական դաշտը ուսումնասիրելու համար կիրառենք մի փորձնական հոսանք, որը շրջանառություն է կատարում շատ փոքր չափեր ունեցող հարթ կոնտուրում:
Տարածության մեջ կոնտուրի կողմնորոշումը բնութագրենք այդ կոնտուրի տարած այնպիսի նորմալի ուղղության միջոցով, որը հոսանքի ուղղության հետ կապված է աջ պտուտակի կանոնով: Այդպիսի նորմալը կանվանենք դրական:
Փորձնական կոնտուրը մագնիսական դաշտ մտցնելով, կնկատենք, որ դաշտը կոնտուրի վրա թողնում է կողմնորոշող ազդեցություն՝
դասավորելով նրան իր դրական նորմալի որոշակի ուղղությամբ: Այդ ուղղությունը ընդունենք որպես դաշտի ուղղություն տվյալ կետում: Եթե կոնտուրը շրջենք այնպես, որ նորմալի եւ դաշտի ուղղությունները
չհամընկնեն, ապա կառաջանա մի պտտող մոմենտ, որը կձգտի կոնտուրը վերադարձնել
իր հավասարակշիռ դիրքը: Մոմենտի մեծությունը կախում ունի նորմալի եւ դաշտի
ուղղության միջեւ եղած ![]() անկյունից, ընդ որում իր ամենամեծ
անկյունից, ընդ որում իր ամենամեծ ![]() արժեքին է հասնում, երբ
արժեքին է հասնում, երբ ![]() (
(![]() դեպքում մոմենտը հավասար է զրոյի):
դեպքում մոմենտը հավասար է զրոյի):
Պտտող մոմենտը կախում ունի ինչպես տվյալ կետում դաշտի հատկություններից, այնպես էլ կոնտուրի հատկություններից: Նույն կետում տարբեր փորձնական կոնտուրներ տեղադրելով, կնկատենք, որ ![]() -ի
մեծությունը համեմատական է կոնտուրում եղած
հոսանքի ուժին ու կոնտուրի
-ի
մեծությունը համեմատական է կոնտուրում եղած
հոսանքի ուժին ու կոնտուրի ![]() մակերեսին բոլորովին կախում չունի կոնտուրի ձեւից:
մակերեսին բոլորովին կախում չունի կոնտուրի ձեւից:
Այսպիսով, հոսանքակիր հարթ կոնտուրի վրա մագնիսական դաշտի ազդեցությունը որոշվում է.
![]()
մեծությամբ, որը անվանում են կոնտուրի մագնիսական մոմենտ:
Բացի ![]() հոսանքի ուժից և
հոսանքի ուժից և
![]() մակերեսից,
կոնտուրը բնութագրվում է նաեւ տարածության մեջ իր ունեցած կողմնորոշումով:
Այդ պատճառով մագնիսական մոմենտը պետք է դիտել որպես մի վեկտոր,
որի ուղղությունը համընկնում է դրական նորմալի ուղղության հետ.
մակերեսից,
կոնտուրը բնութագրվում է նաեւ տարածության մեջ իր ունեցած կողմնորոշումով:
Այդ պատճառով մագնիսական մոմենտը պետք է դիտել որպես մի վեկտոր,
որի ուղղությունը համընկնում է դրական նորմալի ուղղության հետ.
![]()
որտեղ ![]() -ը միավոր վեկտոր է:
-ը միավոր վեկտոր է:
![]() -ի
տարբեր արժեքներ ունեցող փորձնական կոնտուրների վրա դաշտի տվյալ կետում ազդում են տարբեր մեծության
-ի
տարբեր արժեքներ ունեցող փորձնական կոնտուրների վրա դաշտի տվյալ կետում ազդում են տարբեր մեծության ![]() պտտող մոմենտներ:
Սակայն
պտտող մոմենտներ:
Սակայն 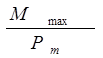 հարաբերությունը բոլոր կոնտուրների համար նույնը կլինի եւ կարող է ընդունվել դաշտը քանակապես բնութագրելու համար:
Այդ հարաբերությանը համեմատական
հարաբերությունը բոլոր կոնտուրների համար նույնը կլինի եւ կարող է ընդունվել դաշտը քանակապես բնութագրելու համար:
Այդ հարաբերությանը համեմատական ![]() ֆիզիկական
մեծությունն անվանում են մագնիսական ինդուկցիա.
ֆիզիկական
մեծությունն անվանում են մագնիսական ինդուկցիա.
![]()
Մագնիսական ինդուկցիան մի վեկտոր է, որի ուղղությունը համընկնում է փորձնական կոնտուրի դրական նորմալի ուղղության հետ' նրա հավասարակշռված դիրքում (այն անվանեցինք դաշտի ուղղություն): (2) բանաձեւը որոշում է ![]() վեկտորի
մեծությունը:
վեկտորի
մեծությունը: ![]() -ն այսինքն բնութագրում է մագնիսական դաշտի ուժային ազդեցությունը
հոսանքի վրա եւ, հետեւաբար էլեկտրական դաշտի
-ն այսինքն բնութագրում է մագնիսական դաշտի ուժային ազդեցությունը
հոսանքի վրա եւ, հետեւաբար էլեկտրական դաշտի ![]() լարվածության նմանակն է, որը բնութագրում է էլեկտրական դաշտի ուժային ազդեցությունը լիցքի վրա:
լարվածության նմանակն է, որը բնութագրում է էլեկտրական դաշտի ուժային ազդեցությունը լիցքի վրա:
Հոսանքի մագնիսական մոմենտ
Այն հոսանքները, որոնց չափերը շատ ավելի փոքր են նրանցից մինչեւ դիտվող կետը եղած հեռավորության համեմատությամբ, այդ հոսանքներին անվանում են տարրական: Նման հոսանքների օրինակ է բոլոր ատոմները, քանի որ նրանցում կան փակ ուղեծրերով պտտվող էլեկտրոններ: Այդ հոսանքներն, ատոմների փոքրության պատճառով, կարելի է ընդունել որպես տարրական հոսանքներ:
Տեսնենք ինչից է կախված տարրական հոսանքի ստեղծած մագնիսական դաշտը:
Ենթադրենք
ունենք ![]() շառավղով
շրջանային
շառավղով
շրջանային ![]() ուժի
հոսանք: Հաշվենք
հոսանքի առանցքի
վրա, նրա կենտրոնից
ուժի
հոսանք: Հաշվենք
հոսանքի առանցքի
վրա, նրա կենտրոնից
![]() հեռավորության
վրա գտնվող ա կետում
դաշտի լարվածությունը:
հեռավորության
վրա գտնվող ա կետում
դաշտի լարվածությունը:
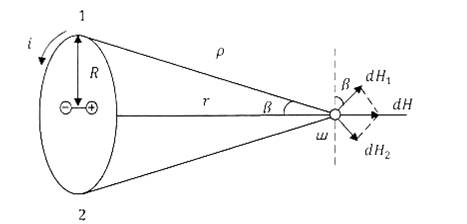
Այս դեպքում
հոսանքի բոլոր
տարրերն ուղղահայաց
են ![]() շառավիղ
վեկտորին եւ այդ
պատճառով
շառավիղ
վեկտորին եւ այդ
պատճառով ![]() բանաձեւում
բանաձեւում![]() : 1 և 2 որեւէ
զույգ տարրերի
ստեղծած
: 1 և 2 որեւէ
զույգ տարրերի
ստեղծած ![]() և
և
![]() մագնիսական
դաշտերը դասավորված
են միեւնույն տրամագծի
վրա և գումարվելով
տալիս են հոսանքի
առանցքի երկարությամբ
ուղղված
մագնիսական
դաշտերը դասավորված
են միեւնույն տրամագծի
վրա և գումարվելով
տալիս են հոսանքի
առանցքի երկարությամբ
ուղղված ![]() դաշտ:
Այդ պատճառով ամբողջ
շրջանային հոսանքի
լրիվ դաշտն էլ
ուղղված է հոսանքի
առանցքով:
դաշտ:
Այդ պատճառով ամբողջ
շրջանային հոսանքի
լրիվ դաշտն էլ
ուղղված է հոսանքի
առանցքով:
Հոսանքի մեկ տարրի ստեղծած դաշտի բաղադրիչը հոսանքի առանցքով կլինի.
![]()
Գումարելով այս արտահայտությունը հոսանքի բոլոր էլեմենտներով, կստանանք.
![]()
որտեղ ![]() հոսանքով
շրջահոսվող մակերեսն
է:
հոսանքով
շրջահոսվող մակերեսն
է:
Եթե հոսանքը
տարրական է, այսինքն,
եթե ![]() , ապա ստացված
բանաձեւում երկրորդ
կարգի փոքրությունների
ճշտությամբ կարելի
է ընդունել
, ապա ստացված
բանաձեւում երկրորդ
կարգի փոքրությունների
ճշտությամբ կարելի
է ընդունել ![]() : Վերջնական
արդյունքը կներկայացվի
հետեւյալ տեսքով.
: Վերջնական
արդյունքը կներկայացվի
հետեւյալ տեսքով.
![]()
որտեղ ![]() ,
իսկ
,
իսկ ![]() -ն մագնիսական
հաստատունն է:
-ն մագնիսական
հաստատունն է:
Եթե ունենայինք
հոսանքի առանցքի
երկարությամբ
ուղղորդված տարրական
էլեկտրական դիպոլ,
ապա նրա ստեղծած
էլեկտրական դաշտն
ուղղորդված կլինի
այնպես, ինչպես
դիտարկված օրինակում
մագնիսական դաշտը,
այսինքն' նույնպես
հոսանքի առանցքով:
Համաձայն ![]() բանաձեւի
այդ դաշտի մեծությունը
(որտեղ անհրաժեշտ
է ընդունել, որ
բանաձեւի
այդ դաշտի մեծությունը
(որտեղ անհրաժեշտ
է ընդունել, որ
![]() ) հավասար
կլիներ
) հավասար
կլիներ
![]()
(2) բանաձեւն ունի
նույն տեսքը, ինչ
որ (1): Այս դեպքում
էլեկտրական դիպոլի
![]() մոմենտի
դերը կատարում
է
մոմենտի
դերը կատարում
է ![]() արտադրյալը,
որը ստացել է հոսանքի
մագնիսական մոմենտ
անվանումը: Դիպոլի
էլեկտրական մոմենտը
վեկտոր է, հոսանքի
մագնիսական մոմենտը
նույնպես վեկտոր:
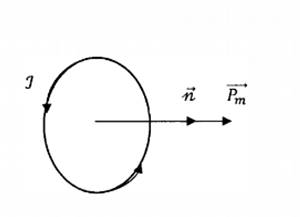
Որպես մագնիսական
մոմենտի ուղղություն
ընդունվում է գալարի
հարթության դրական
նորմալի ուղղությունը:
Եթե
արտադրյալը,
որը ստացել է հոսանքի
մագնիսական մոմենտ
անվանումը: Դիպոլի
էլեկտրական մոմենտը
վեկտոր է, հոսանքի
մագնիսական մոմենտը
նույնպես վեկտոր:
Որպես մագնիսական
մոմենտի ուղղություն
ընդունվում է գալարի
հարթության դրական
նորմալի ուղղությունը:
Եթե ![]() -ը նորմալի
երկարությամբ
միավոր վեկտորն
է, ապա հոսանքի
-ը նորմալի
երկարությամբ
միավոր վեկտորն
է, ապա հոսանքի
![]() մագնիսական
մոմենտը
մագնիսական
մոմենտը
![]()
Հոսանքների մագնիսական Փոխազդեցության օրենքը
(Ամպերի օրենքը)
Ամպերի փորձերում
հաստատվել էր,
որ երկու հաղորդիչների
փոխազդեցությունը
համեմատական է
յուրաքանչյուր
հաղորդչով հոսող
հոսանքի ուժին:
Մագնիսական դաշտ
չի դիտվում այն
դեպքում, երբ հաղորդալարի
մի մասը փաթաթում
ենք մյուսի շուրջը:
Այս արդյունքներից
հետեւում է, որ
հաղորդալարի որեւէ
![]() ,
, ![]() եւ
եւ
![]() տարրեր
համատեղ ստեղծում
են նույնպիսի մագնիսական
ազդեցություն,
ինչպիսին ունի
այդ հատվածները
փակող dl մեկ տարրը:
տարրեր
համատեղ ստեղծում
են նույնպիսի մագնիսական
ազդեցություն,
ինչպիսին ունի
այդ հատվածները
փակող dl մեկ տարրը:
Ասվածից հետեւում
է, որ հաղորդչի
անսահման փոքր
հարվածի մագնիսական
ազդեցությունը
կախված է ![]() արտադրյալից,
որտեղ
արտադրյալից,
որտեղ ![]() ֊ն հոսանքի
ուժն է, իսկ
֊ն հոսանքի
ուժն է, իսկ ![]() -ը հոսանքի
ուղղությունն
ու
-ը հոսանքի
ուղղությունն
ու ![]() հատվածի
երկարությունն
ունեցող վեկտոր
է: Այդ արտադրյալը
անվանում են հոսանքի
տարր:
հատվածի
երկարությունն
ունեցող վեկտոր
է: Այդ արտադրյալը
անվանում են հոսանքի
տարր:
Հոսանքի տարր
հասկացությունը
մագնիսական փոխազդեցության
օրենքներում խաղում
է նույն դերը, ինչ
որ կետային լիցքի
հասկացությունը
էլեկտրական փոխազդեցության
օրենքում: Որեւէ
![]() հոսանքի
տարրի
հոսանքի
տարրի ![]() ուժը,
որով այն ազդում
է մի այլ
ուժը,
որով այն ազդում
է մի այլ ![]() հոսանքի
տարրի վրա, համեմատական
է հոսանքի տարրերից
յուրաքանչյուրին,
այսինքն` նրանց
արտադրյալին.
հոսանքի
տարրի վրա, համեմատական
է հոսանքի տարրերից
յուրաքանչյուրին,
այսինքն` նրանց
արտադրյալին.
![]()
Այդ ուժը կախված
է նաեւ հոսանքի
տարրերի միջեւ
եղած ![]() հեռավորությունից:
հեռավորությունից:
Ամպերը ենթադրեց,
որ այն հակադարձ
համեմատական է
հեռավորության
որեւէ ![]() աստիճանին
եւ փորձերից եզրակացրեց,
որ
աստիճանին
եւ փորձերից եզրակացրեց,
որ ![]()
![]()
Հոսանքի երկու տարրերի փոխազդեցության ուժի մեծությունը եւ ուղղությունը կախված են նաեւ նրանց փոխադարձ կողմնորոշումից: Այդ կախման որոշումն պահանջեց տարբեր գիտնականների մի շարք հետազոտություններ:
Նախ դիտարկենք
այն դեպքը, երբ
հաղորդիչների
![]() եւ
եւ ![]() հատվածները
գտնվում են միեւնույն
հարթությունում
եւ
հատվածները
գտնվում են միեւնույն
հարթությունում
եւ ![]() նշանակենք
առաջին հատվածից
երկրորդը տարված
շառավիղ-վեկտորը:
նշանակենք
առաջին հատվածից
երկրորդը տարված
շառավիղ-վեկտորը:
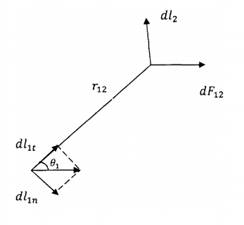
![]() հատվածի
ազդեցությունը
փոխարինենք նրա
հատվածի
ազդեցությունը
փոխարինենք նրա
![]() եւ
եւ ![]() բաղադրիչների
բաղադրիչների
ազդեցությամբ,
որոնցից մեկն ուղղված
է դեպի ![]() շառավիղ-վեկտորը,
իսկ մյուսը' նրան
ուղղահայաց:
շառավիղ-վեկտորը,
իսկ մյուսը' նրան
ուղղահայաց: ![]() հատվածը
չի թողնում ոչ
մի ազդեցություն
հատվածը
չի թողնում ոչ
մի ազդեցություն
![]() -ի վրա,
-ի վրա, ![]() -ի ցանկացած
կողմնորոշման
դեպքում: Հետեւաբար
-ի ցանկացած
կողմնորոշման
դեպքում: Հետեւաբար
![]() վրա ազդող
ուժը համեմատական
է
վրա ազդող
ուժը համեմատական
է ![]() , որտեղ
, որտեղ
![]() -ը
-ը ![]() եւ
եւ
![]() վեկտորների
կազմած անկյունն
է
վեկտորների
կազմած անկյունն
է ![]() :
:
Ընդհանուր
դեպքում հաղորդիչների
![]() եւ
եւ ![]() հատվածները
կարող են գտնվել
միեւնույն հարթության
մեջ: Այդ դեպքում
հատվածները
կարող են գտնվել
միեւնույն հարթության
մեջ: Այդ դեպքում
![]() հատվածը
կարելի է տրոհել
երկու բաղադրիչների,
որոնցից մեկը`
հատվածը
կարելի է տրոհել
երկու բաղադրիչների,
որոնցից մեկը`
![]() -ն գտնվում
է
-ն գտնվում
է ![]() եւ
եւ ![]() պարունակող
հարթության մեջ,
իսկ մյուսը`
պարունակող
հարթության մեջ,
իսկ մյուսը` ![]() -ը ուղղահայաց
է այդ հարթությանը:
-ը ուղղահայաց
է այդ հարթությանը:
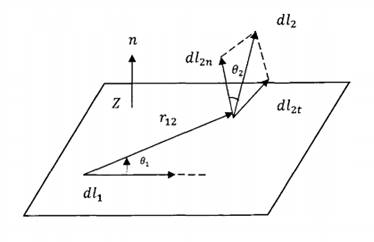
Փորձերը բերում
են այն հետեւության,
որ ի վրա ազդող
ուժը միշտ հավասար
է զրոյի: Հետեւաբար,
![]() -ի վրա ազդող
ուժը համեմատական
է
-ի վրա ազդող
ուժը համեմատական
է ![]() բաղադրիչին,
որտեղ
բաղադրիչին,
որտեղ ![]() -ը անկյունն
է
-ը անկյունն
է ![]() վեկտորի
և
վեկտորի
և ![]() հարթության
հարթության
![]() նորմալի
միջև.
նորմալի
միջև.
![]()
Բոլոր արդյունքները միավորելով մի բանաձեւում կգրենք.
![]()
Այստեղ ![]() -ն համեմատականության
գործակից է եւ
կախված է միավորների
ընտրությունից:
(1) բանաձեւով արտահայտվում
է
-ն համեմատականության
գործակից է եւ
կախված է միավորների
ընտրությունից:
(1) բանաձեւով արտահայտվում
է ![]() ուժի մեծությունը:
Այդ ուժի ուղղությունը
որոշվում է հետեւյալ
կանոնով. հոսանքի
2 տարրի վրա ազդող
ուժը ուղղահայաց
է այդ տարրին եւ
գտնվում է հոսանքի
1 տարր եւ
ուժի մեծությունը:
Այդ ուժի ուղղությունը
որոշվում է հետեւյալ
կանոնով. հոսանքի
2 տարրի վրա ազդող
ուժը ուղղահայաց
է այդ տարրին եւ
գտնվում է հոսանքի
1 տարր եւ ![]() շառավիղ
վեկտոր պարունակող
անկյան մեջ:
շառավիղ
վեկտոր պարունակող
անկյան մեջ:
Ուժի ուղղությունը
ենթարկվում է նաեւ
աջ խցանահանի կանոնին.
եթե աջ ակոսով
խցանահանը պտտենք
այնպես, որ նրա
բռնակը շարժվի
հոսանքի 2 տարրից
դեպի ![]() ուղղահայացը,
ապա խցանահանի
համընթաց շարժումը
համընկնում է
ուղղահայացը,
ապա խցանահանի
համընթաց շարժումը
համընկնում է ![]() ուժի ուղղությանը:
ուժի ուղղությանը:
![]() նորմալի
ուղղությունը
նույնպես որոշվում
է այդ կանոնով,
այն համընկնում
է խցանահանի համընթաց
շարժմանը, եթե
այն պտտում ենք
1 տարրից դեպի
նորմալի
ուղղությունը
նույնպես որոշվում
է այդ կանոնով,
այն համընկնում
է խցանահանի համընթաց
շարժմանը, եթե
այն պտտում ենք
1 տարրից դեպի ![]() շառավիղ-վեկտորը:
շառավիղ-վեկտորը:
Օգտվելով վեկտորային արտադրյալից (1)-ը կգրենք.
![]()
(1)-ը եւ (1') ֊ը բանաձեւերով արտահայտված Ամպերի օրենքը հիմնականն է մագնիսականության մեջ եւ կատարում է այն դերը, ինչ որ Կուլոնի օրենքը էլեկտրաստատիկայում: Օգտվելով այդ օրենքից կարելի է հաշվել փոխազդեցության ուժը հոսանքի այն տարրերի միջեւ, ըստ որոնց կարելի է վերլուծել ցանկացած փակ հաղորդիչները, իսկ գումարելով այդ ուժերը հոսանքի բոլոր տարրերի համար, կարելի է հաշվել նաեւ փոխազդեցության ուժը վերջավոր չափեր ու ցանկացած ձեւ ունեցող կոնտուրների միջեւ:
Եզրակացություն
Այսպիսով
լիցքավորված մասնիկն
իր շուրջը ստեղծում
է էլեկտրական դաշտ,
լիցքավորված մասնիկների
ուղղորդված շարժումն
ստեղծքւմ է էլեկտրական
հոսանք, իսկ լիցքավորված
շարժվող մասնիկն
իր շուջը ստեղծում
է մագնիսական դաշտ,
որը բնութագրվում
է ![]() հոսանքի
էլեմենտով: Հոսանի
էլեմենտների գոյությամբ
և վերադրմամբ են
ստեղծվում մագնիսական
դաշտերը: Մագնիսական
դաշտը կախված է
ոչ միայն դաշտը
ստեղծող հոսանքով,
այլ նաև կախված
է հեռավորությունից
(դիրքից):
հոսանքի
էլեմենտով: Հոսանի
էլեմենտների գոյությամբ
և վերադրմամբ են
ստեղծվում մագնիսական
դաշտերը: Մագնիսական
դաշտը կախված է
ոչ միայն դաշտը
ստեղծող հոսանքով,
այլ նաև կախված
է հեռավորությունից
(դիրքից):
Այն դիրքը, որն ընդունում է հոսանքակիր հաղորդիչը, անվանում են մագնիսական դաշտի ուղղություն:
Դաշտի պարամետրերը ժամանակից կախված չեն փոխվում:
Գրականություն
1. Ս.Բ. Կալաշնիկով «էլեկտրականություն»: « Միտք » հրատ. Երեւան 1968թ.
2. Ի.Վ Սավելև «Ըեւդհաեւուր ֆիզիկայի դա սընթա ց» II հատոր: «Լույս» հրատ. 1977թ.
3. Ռ.Գ. Գևորգյան, Վ Վ Շեպել «Ընդհանուր ֆիզիկայի դասընթաց» Երեւան 1970թ.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.