
Қазақстан Республикасының Білім және ғылым министрлігі
Шығыс Қазақстан облыстық әкімшілігі Білім басқармасының
«Көлік колледжі» коммуналдық мемлекеттік қазыналық кәсіпорын

Жұмыс дәптері №1
Математика пәнінен
Бөлім: Функция, оның қасиеттері және графигі
Дайындаған_________оқытушы: Жумадилова Ж.Ш.
Жұмыс дәптері жалпы білім беру пәндерінің
циклды комиссиясында қарастырылды.
№____ хаттама «___»______ 2021 жыл
Циклды комиссияның төрайымы:____Слямова А.Т.
Семей 2020-2021 оқу жылы
МАЗМҰНЫ.
беті.
КІРІСПЕ............................................................................................. 3
Тақырып 1. Функцияның берілу тәсілдері мен графигі.
Функция графигін түрлендіру арқылы салу............ 4
Тақырып 2. Функция қасиеттері................................................. 9
Тақырып 3. Бөлшек-сызықты функция...................................... 14
Тақырып 4. Күрделі және кері функция ұғымдары.................. 16
Сәйкестендіруге арналған есептер мен тапсырмалар.................. 19
Тақырыпты қортындылауға тест сұрақтары................................. 22
Қолданылған әдебиеттер тізімі ................................................. 24
Кіріспе
Функция аса маңызды математикалық ұғымдардың бірі және де ол заттар мен құбылыстардың өзара байланысын бейнелейді.Бүгінде функцияны анықтаудың әр түрлі жолдары белгілі. Солардың бірінде функция ұғымы бастапқы ұғым ретінде алынады. Бейнелеулер, қатынастар және сәйкестіктер табиғаты әр түрлі жиындарда берілуі мүмкін екендігі белгілі, ендеше олардың дербес түрі болып табылатын функцияның да анықталу облысы мен мәндерінің облысы әр түрлі жиындар бола алады. Ал математика курсында негізінен сандық және нүктелік жиындар қарастырылады, өйткені осы жиындарда функцияның әр түрлі қасиеттерін қарастыру өте қолайлы. Функцияны әр түрлі тәсілмен анықтап береді. Соның ішінде ең көп тарағы – функцияның аналитикалық тәсілмен берілуі, яғни аргументтің мәні бойынша функцияның сәйкес мәнін табу кезінде орындалатын амалдардың жиынтығын көрсететін формула арқылы функцияның берілуі. Сонда функцияның анықталу облысы көрсетіледі. Егер формула арқылы берілген функцияның анықталу облысы айқын түрде көрсетілмесе және ешқанда қосымша шектеулер келтірілмесе, онда функцияның анықталу облысы, айнымалының осы формуланың мән-мағынасы болатындай барлық мәндерінен тұрады. Функцияны аргументтің мәндері және функцияның сәйкес мәндері арасындағы сәйкестік заңын сөз арқылы сипаттаудың келтіруімен де анықтап беруге болады. Осындай функциялар үшін арнайы таңбалардың да енгізілуі орынды. Функцияны, оның графигі деп аталатын, координаттық жазықтың қандай да бір сызығының көмегімен анықтап беруге болады. Жалпы алғанда, әрбір функциямен қандай да бір сызық – осы функциның графигі байланысты. Алайда бұған кері ұйғарым әрдайым тура бола бермейді, өйткені xєX болатын x-тің берілген мәнінде оған сәйкес келктін функцияның бір ғана мәні y бар болады. Сондықтан ордината осіне параллель жүргізілген әрбір түзуде функцияның графигіне тиісті бірден артық болмайтын нүкте ғана жатуы тиіс. Мәселен, шеңбер қанда да бір функциның графигі болып табылмайды, өйткені шеңбердің екі нүктесі жататын ордина осіне параллель түзулер бар. Кейбір жағдайларда, аргументің таңдап алынған мәндерінде функцияның мәндерін табуға мүмкіндік беретіндей кесте құруға болады. Осындай кестелердің мысалдары ретінде сандардың квадраттарының және кубтарының кестелерін, тригонометриялық функциялар мәндерінің кестелерін және т.б. атаған жөн. Әсіресе, X жиыны шектеулі болса, онда анымалылардың сәйкес мәндерінің кестелерін пайдаланған тым қолайлы Бұл жағдайда функция кестелік тәсіл арқылы анықтап берілген болып табылады. Дегенмен функцияның ананлитикалық және графигтік тәсілдермен берілуі оны оқып-үйренуге өте қолайлы. Осыған орай, аналитикалық тәсілмен берілетін нақты функцияларды анықтайық. Біз оларды мынадай ретпен оқып-үйренеміз:а/ қандай да бір функцияға киліктіретін, яғни оны енгізу себепші болатын нақты жағдайларды қарастырамыз;
ә/ функцияның анықтамасын тұжырымдаймыз және оны формуламен анықтап береміз де, осы формуланың құрамындағы параметрлерді зерттейміз;
б/ оқып-үйренетін функцияны график арқылы кескіндеп көрсетеміз;
в/ функцияның кейбір касиеттерін қарастырамыз.
Тақырып 1: Функцияның берілу тәсілдері мен графигі.
Функция графигін түрлендіру арқылы салу.
Анықтама: Егер х-тің әрбір мәніне у-тің
жалғыз ғана мәні сәйкес болса, онда у
айнымалысының х-айнымалысынан тәуелділігі функция деп аталады.х-
айнымалысын тәуелсіз айнымалы немесе аргумент деп, ал у- айнымалысын
тәуелді айнымалы деп атайды. Берілген х-тің мәніне
сәйкес у-тің мәнін функцияның мәні деп аталады.
Тәуелсіз айнымалы қабылдайтын мәндердің бәрі
функцияның анықталу облысын құрайды. ![]() функциясы қабылдайтын
мәндердің бәрі функцияның мәндерін
қабылдайды.
функциясы қабылдайтын
мәндердің бәрі функцияның мәндерін
қабылдайды.
Функцияның берілу тәсілдері:
1. Функцияның аналитикалық берілуі
Функцияны беру үшін аргументтің әрбір мәніне сәйкес келетін функцияның мәнін табуға мүмкіндік беретін тәсілді көрсету керек. Ең көп қолданылатын тәсіл функцияның формула арқылы берілу тәсілі болады.
2.Функцияның кестелік берілуі
Практикада функцияның кестелік берілуі жиі қолданылады. Бұл тәсілде аргументтің белгілі мәндеріне сәйкес функцияның мәндері көрсетілген кесте келтіріледі.
3. Функцияның графиктік берілуі
Функцияның графигі деп координаталық жазықтықтағы абсциссалары функция аргументіне тең, ал ординаталары функцияның сәйкес мәндеріне тең нүктелердің жиынынан тұратын сызбаны айтады.
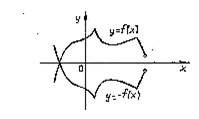
Функция графигін түрлендіру арқылы салу
![]()
![]()
![]() функциясының графигін біле отырып,
қарапайым геометриялық түрдендірулер арқылы
көптеген басқа функциялардың графиктерін салуға болады.
Ең негізгілеріне тоқталып өтейік.
функциясының графигін біле отырып,
қарапайым геометриялық түрдендірулер арқылы
көптеген басқа функциялардың графиктерін салуға болады.
Ең негізгілеріне тоқталып өтейік.
![]()
 1 .
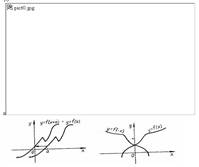
1 . ![]() функциясының графигі
функциясының графигі ![]() функциясының графигінен
функциясының графигінен ![]() осіне қарағанда симметриялы болады
(бұл симметрияда әрбір
осіне қарағанда симметриялы болады
(бұл симметрияда әрбір ![]() нүкте ординатасы
қарама-қарсы
нүкте ординатасы
қарама-қарсы ![]() нүктеге көшеді).
нүктеге көшеді).
2. ![]() функциясының графигі
функциясының графигі![]() функциясының графигін
функциясының графигін ![]() осіне
осіне
![]() қарағанда симметриялы болады
(бұл симметрияда әрбір
қарағанда симметриялы болады
(бұл симметрияда әрбір ![]() нүкте қарама-қарсы
нүктеге көшеді).
нүкте қарама-қарсы
нүктеге көшеді).
 3.
3. ![]() функциясының графигі,
функциясының графигі, ![]() болғанда
болғанда ![]() функциясының графигінің
әрбір нүктесінің ординатасын
функциясының графигінің
әрбір нүктесінің ординатасын ![]() санына көбейту, яғни
санына көбейту, яғни ![]() осіне қарай
осіне қарай ![]() қатынаста сығу арқылы (
қатынаста сығу арқылы (![]() болғанда, ондай сығу
болғанда, ондай сығу ![]() есе созылады). Егер
есе созылады). Егер ![]() болса, ондай да сәйкес түрлендіру
болса, ондай да сәйкес түрлендіру
![]() осіне қарағанда симметриялы
және сол оське қарай
осіне қарағанда симметриялы
және сол оське қарай ![]() қатынасында сығу композициясы
кез-келген ретпен болып табылады.
қатынасында сығу композициясы
кез-келген ретпен болып табылады.
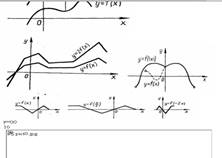
4. ![]() функциясының графигі
функциясының графигі ![]() ,
,![]() ,
, ![]() болғанда графиктері келесідей болады.
болғанда графиктері келесідей болады.
 5 .
5 . ![]() функциясы графигінің әрбір
нүктесінің ординатасын бір ғана
функциясы графигінің әрбір
нүктесінің ординатасын бір ғана ![]() шамаға арттырсақ,
шамаға арттырсақ, ![]() функциясы графигі шығады. Сонымен,
функциясы графигі шығады. Сонымен,
![]() функциясының графигі
функциясының графигі ![]() функциясы графигінін
функциясы графигінін ![]() осі бойымен
осі бойымен ![]() шамаға параллель көшіру
арқылы, яғни
шамаға параллель көшіру
арқылы, яғни![]() координаталары
қашықтыққа көшіру арқылы
координаталары
қашықтыққа көшіру арқылы
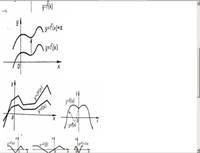 табылады, ал
табылады, ал ![]() функциясы графигі
функциясы графигі![]() қашықтыққа
көшіру арқылы табылады.
қашықтыққа
көшіру арқылы табылады.
6. ![]() функциясы графигі бойынша
функциясы графигі бойынша ![]() функциясы графигін
функциясы графигін ![]() координаталарын
координаталарын ![]() осі бойымен параллель көшіру
арқылы, ал
осі бойымен параллель көшіру
арқылы, ал ![]() функциясының графигін
функциясының графигін![]() координаталарын
координаталарын ![]() осі
осі
бойымен параллель көшіру арқылы табылады.
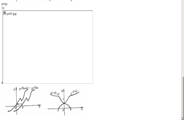 7. Функцияның
7. Функцияның ![]() болғанда графигі
болғанда графигі ![]() функциясы графигінің
функциясы графигінің ![]() осінен жоғары орналасқан (ол
үшін
осінен жоғары орналасқан (ол
үшін ![]() бөлігі мен
бөлігі мен ![]() қалған бөлігінің
қалған бөлігінің ![]() осіне
осіне  қарағандағы симметрияда
шығатын бейнесінің бірігуінен тұрады).
қарағандағы симметрияда
шығатын бейнесінің бірігуінен тұрады).
8 . Мына функцуияның ![]() графигін салу үшін
графигін салу үшін ![]() функциясы графигінің
функциясы графигінің ![]() осінің оң жағында
жатқан бөлігі мен осы бөліктің
осінің оң жағында
жатқан бөлігі мен осы бөліктің ![]() осіне қарағандағы
симметрияда шығатын бейнесін біріктіру керек.
осіне қарағандағы
симметрияда шығатын бейнесін біріктіру керек.
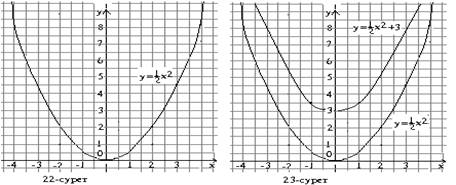
![]() функциясының графигі 22-суретте
кескінделген.
функциясының графигі 22-суретте
кескінделген.
Аргументтің осы мәндеріне арналған ![]() функция мәндерінің кестесін
құру үшін
функция мәндерінің кестесін
құру үшін ![]() функциясының табылған
мәндеріне 3-ті қосу жеткілікті . Координатала-ры естеде берілген
нүктелерді қоссақ,
функциясының табылған
мәндеріне 3-ті қосу жеткілікті . Координатала-ры естеде берілген
нүктелерді қоссақ, ![]() +3 функциясының графигін аламыз (23
–сурет)
+3 функциясының графигін аламыз (23
–сурет) ![]() функциясының графигі
функциясының графигі ![]() функциясының графигін жогары қарай
жылжыту нәтижесінде алынган парабола.
функциясының графигін жогары қарай
жылжыту нәтижесінде алынган парабола.
Жалпы алғанда, ![]() функциясының грфигі
функциясының грфигі ![]() функциясының графигінен у осінің
бойымен ( егер n>0 болса ) n бірлік жоғары қарай немесе ( егер
n<0 болса) n бірлік төмен қарай параллель көшіру
арқылы алуға болады.
функциясының графигінен у осінің
бойымен ( егер n>0 болса ) n бірлік жоғары қарай немесе ( егер
n<0 болса) n бірлік төмен қарай параллель көшіру
арқылы алуға болады. ![]() функциясының графигі
функциясының графигі ![]() функциясының графигінен х осінің
бойымен оңға қарай mбірлік (мұндағы m>0)
немесе солға қарай m бірлік (мұндағы m<0 ) параллель
көшіру арқылы алынады. Мысалы,
функциясының графигінен х осінің
бойымен оңға қарай mбірлік (мұндағы m>0)
немесе солға қарай m бірлік (мұндағы m<0 ) параллель
көшіру арқылы алынады. Мысалы, ![]() функциясын қарастырайық. Ол
үшін
функциясын қарастырайық. Ол
үшін ![]()
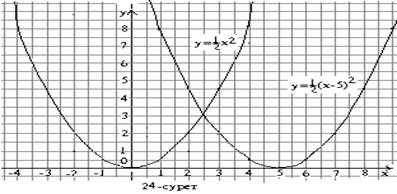
![]() функциясының графигін саламыз (24-
сурет). Осыдан кейін
функциясының графигін саламыз (24-
сурет). Осыдан кейін ![]() функциясының мәндерінің
кестесін құрып, графигін саламыз.
функциясының мәндерінің
кестесін құрып, графигін саламыз. ![]() және
және ![]() функцияларының графигін бір
координаталық жазықтыққа саламыз (24-сурет).
функцияларының графигін бір
координаталық жазықтыққа саламыз (24-сурет).
![]() функциясының графигі
функциясының графигі ![]() функциясының графигін оңға
қарай жылжыту нәтижесінде алынған парабола.
функциясының графигін оңға
қарай жылжыту нәтижесінде алынған парабола.
![]() функциясының графигі екі параллель
көшіру арқылы х осі бойымен оңға қарай m бірлік
(m>0 болса) немесе солға қарай –m бірлік (m<0 болса)
және у осібойымен жогары қарай n бірлік (n>0болса) немесе
төмен қарай – n бірлік (n>0 болса ) жылжыту арқылы
функциясының графигі екі параллель
көшіру арқылы х осі бойымен оңға қарай m бірлік
(m>0 болса) немесе солға қарай –m бірлік (m<0 болса)
және у осібойымен жогары қарай n бірлік (n>0болса) немесе
төмен қарай – n бірлік (n>0 болса ) жылжыту арқылы ![]() функциясының графигінен алынатын парабола.
Мысалы,
функциясының графигінен алынатын парабола.
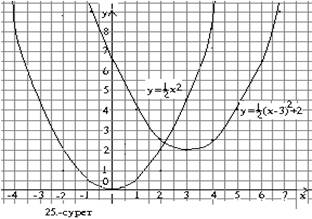
Мысалы, ![]() функциясының графигін екі паралльл
көшіру арқылы:
функциясының графигін екі паралльл
көшіру арқылы:![]() параболасын 3бірлік оңға
қарай және 2 бірлік жоғары қарай жылжыту арқылы
алуға болады.(25-сурет).
параболасын 3бірлік оңға
қарай және 2 бірлік жоғары қарай жылжыту арқылы
алуға болады.(25-сурет).
Тапсырмалар:
Жоғарыда берілген мысалдарға ұқсас функцияның графигін салуға арналған есептер жеткілікті берілген. Тақырыпты тиянақты және толық меңгеруге арналған күрделірек есептерді шығарыңыз.
1.![]() функциясының
графигін пайдаланып, мына функциялардың графигін салыңыз?
функциясының
графигін пайдаланып, мына функциялардың графигін салыңыз?
а) ![]() ;
;
б) ![]() .
.
2.![]() функциясының графигін пайдаланып, мына
функциялардың графигін салыңыз:
функциясының графигін пайдаланып, мына
функциялардың графигін салыңыз:
а) ![]() ;
;
б) ![]() ?
?
3.y=x3 функциясының графигін қолданып, y=f(x) функциясының графигін салыңдар:
а) f(x)=x3+4
ә) f(x)=-x3-3
б) f(x)=-2x3+1
в)f(x)=2(x-1)3-5
4.y=2(3+x)2-5 функциясының графигін y=x2 функциясының графигінен қандай түрлендірулер жүргізу арқылы алуға болады? Графигін салыңдар.
y=x2-2x және y= -1
5. Берілген функциялардың графиктерінің ортақ нүктелері болатынын графиктің көмегімен көрсетіңдер.
y=x2-5x+4 және y= -3/x
Тақырып 2: Функция қасиеттері.
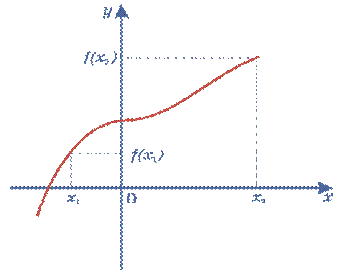
2-сурет
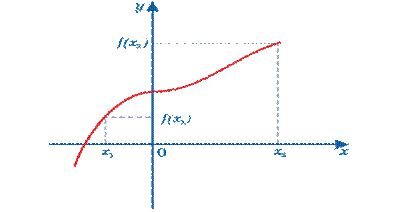
Ықшамдалған 1-анықтаманы келесі тәсілдердің бірімен түсіндіруге болады (2-сурет):
-
аргументтің үлкен мәніне функцияның үлкен
мәні сәйкес келеді;
- егер х өссе, онда у те өседі;
- x артқан сайын, f(x) те артады.
2-анықтама: Қандай да бір аралықтан алынған кез-келген x1 және x2 сандары үшін, x2>x1 болғанда, f(x2)≥f(x1) тереңдігі орындалса, онда осы аралықта у=f(x) функциясы кемімейтін функция деп аталады.
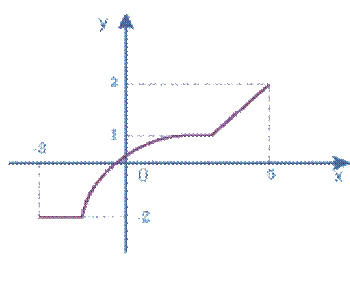
3-сурет
Қандай да бір аралықтан алынған кез-келген x2 және x1 сандары үшін, x2>x1болғанда, f(x1)>f(x2) тереңдігі орындалса, онда осы аралықта у=f(x) функциясы кемімелі функция деп аталады.
Кемімелі функция анықтамасының ықшамдалған түрі:
– аргументтің үлкен мәніне
функцияның кіші мәні сәйкес келеді;
– егер х өссе, онда у кемиді.
– х артқан сайын, f(x) кемиді.
4-ші және 5-ші суреттерде тек қана
кемімелі және өспелі функцияларға сәйкес мысалдар
келтірілген.
Біз ары қарай анықталу облысы сан түзуі немесе
олардың бірігуі болатын функцияларды қарастырамыз (кесінділер жайлы
дәлірек оқулықтың соңында «Сан
түзуінің жиындары» жалы берілген қосымшадан қарай
аласыздар).
Бізге алдағы уақытта
төмендегі анықтама өте қажет.
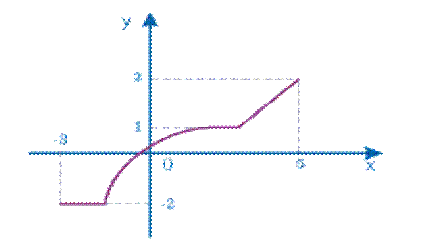
4-сурет
5-анықтама Функцияның анықталу облысы кесінді немесе кесінділердің бірігуі болсын. Егер саны анықталу облысындағы кесіндіге немесе кесінділердің бірігуіне тиісті болып, бірақ осы кесінділердің ешқайсыларының ұштары болмаса, ол ол анықталу облысының ішкі нүктесі деп аталады.
5-сурет
10-суреттегі функцияның анықталу
облысы кесіндісі. –4 және 4 сандары кесіндінің ұштары, олар
анықталу облысының ішкі нүктелері бола алмайды.
қалған барлық нүктелері анықталу облысының
ішкі нүктелері болып табылады.
Бізге берілген функциялардың өсу аралықтары, кему
аралықтары табылатын
болсын делік.
Бізге берілген функциялардың өсу аралықтары, кему аралықтары табылатын
болсын делік.
Локальді минимум және локальді максимум
нүктелерді локальді экстремум нүктелер деп аталады.
«Локальді минимум», «локальді максимум», «локальді экстремум»
сөздерінің орнына тек қана «минимум», «максимум», «экстремум»
сөздерін пайдалануға болады.
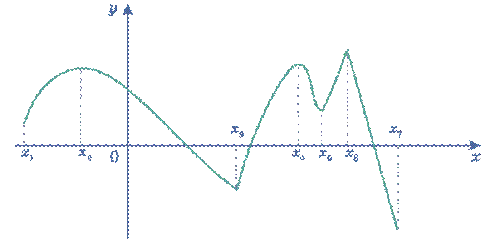
[x1;x7] кесіндісінде анықталған қандай да бір f(x) функциясының графигін қарастырамыз (6-сурет). х1, х7 нүктелері экстремум нүктелері болмайды өйткені олар [x1;x7] жиынының ішкі нүктелері емес. х2, х4, х6 – нүктелері локальді максимум нүктелері, ал х3, х5 – локальді минимум нүктелері болады.
6-сурет
f(x)=x2-|x| функциясы жұп болып табыладыма?
Есептің шартында анықталу облысы жайында еш нәрсе айтылмағандықтан, наұты анықталу облысы, яғни х2-|x|өрнегінің ММО(мүмкін мәндер облысы) алынады. Берілген өрнекте х тің мүмкін мәндер облысында ешқандай шектеу қойылмаған , сондықтан , яғни f(x) функциясының анықталу облысы барлық нақты сандар
жиыны болып табылады. Нөл нүктесі симметрия центрі болады. Жұп функция анықтамасының 1- шарты орындалады.енді 2- шартын тексерсек , кез келген х үшін мына шарт орындалды:
F(-x)2=|-x|=x2-|x|=f(x) - таңбасын дұрыс жазу керек.
Шешімі : жиыны нолге қатысты симметриялы. Кез келген х үшін f(-x)=f(x) теңдігі орындалады. Шынында да f(-x)=(-x)2-(-x)=x2-|x|=f(x)
Жауабы: f(x)=x2-|x| жұп функция болады
Есепті басқа тәсілмен – оның
графигін салу арқылы шешуге болады (12-сурет):
Бұл өте қарапайым мысал, бірақ бұл функцияның
қарастырылып отырған анықталу облысы, функцияның
қасиеттеріне айтарлықтай әсер ететінін көрсететін
көрнекі иллюстрация болып табылады. Бірдей аналитикалық формуламен
берілген, бірақ әртүрлі анықталу облыстарында
қарастырылатын функциялардың әртүрлі функциялар
болатынын ескерген жөн. Егерде мысалдағы (–2;1) жиынын кез келген
(–a;a), a > 0 жиынына өзгертсек, онда функция жұп болар еді.
Енді тақ функцияларға тоқталайық.
2-анықтама:Егер төменгі екі шарт орындалса, f(x) функциясы тақ функция деп аталады:
1) D(f) анықталу облысынан алынған кез келген х саны үшін табылған –x саны да D(f)-ке тиесілі болады.
2) кез келген x∈D(f) саны үшін f(–х)=–f(x) теңдігі орындалады.
1) шарт D(f) жиынының координаттар басына қатысты симметриялы екенін білдіреді. Басқаша айтқанда, Ох осіндегі қарама-қарсы абсцисеалары бар кез-келген жұбындағы екі сан да D(f) анықталу облысында жатады, немесе екеуі де D(f) анықталу облысында жатпайды. Екінші жағдайда, осы нүктелердегі функцияның мәндері қарама-қарсы сандар болады. Бұл, егер қандай да бір (x0, y0) нүктесі координаттар жазықтығындағы тақ функцияның графигіне тиесілі болса, онда (–x0, –y0) нүктесі де осы функцияның графигіне тиесілі болады дегенді білдіреді.
Мұндай нүктелер жұбы бір-біріне O(0;0) нүктесіне қатысты симметриялы. Демек, координаттар басы кез келген тақ функция графигінің симметрия центрі болады.
Функция тақ па, жұп па ?
1. у=5х2+3х4
2. у=2х3-7х5
3. у=3х2+cosx
4. Анықталу облысын табыңдар:
f(x)=1/x-1
A) x=2 B) x=1 C) x≠1 Д) x1 E) x
5. 2) Функцияның жұп, тақ екенін анықта:
у=х3-х5+2х
6. А) жұп В) тақ С) периодты Д) периодсыз Е) жұп та, тақ та емес
Берілген функцияға кері функцияны табыңдар:
у=5/x+1
А) у=4х В) у=х-2 С) у=2х+5 Д) у=5/x-1 Е) у=4-х/2
7. Функцияның берілген нүктедегі мәнін табыңдар:
f(x)=√x2-3x+1 f(0) - ?
Тақырып 3: Бөлшек-сызықты функция.
Анықтама: 𝒚=![]() функциясы берілсе,
мұндағы a,b,c,d- нақты сандар (c ≠ 0 немесе 𝑎𝑐≠𝑏𝑑), онда
мұндай функцияларды бөлшек-сызықтық функция деп атайды.
функциясы берілсе,
мұндағы a,b,c,d- нақты сандар (c ≠ 0 немесе 𝑎𝑐≠𝑏𝑑), онда
мұндай функцияларды бөлшек-сызықтық функция деп атайды.
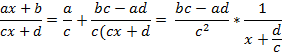
α=-![]() β=
β=![]() 𝑘=
𝑘=![]() деп алсақ,
онда
деп алсақ,
онда ![]() =𝛽+
=𝛽+![]()

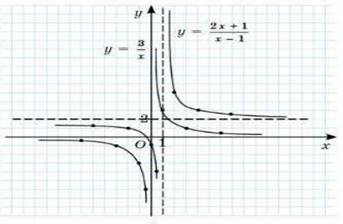
y=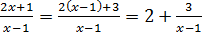 түріне келтіреміз , онда у=
түріне келтіреміз , онда у=![]() функцияның графигін у=
функцияның графигін у=![]() функциясының графигін Ох бойымен 1 бәрлікке
оңға және Оу бойымен 2 бірлікке жоғары параллель
көшіру арқылы алуға болады төмендегі графикте
көрсетілген.
функциясының графигін Ох бойымен 1 бәрлікке
оңға және Оу бойымен 2 бірлікке жоғары параллель
көшіру арқылы алуға болады төмендегі графикте
көрсетілген.
 =
=
=

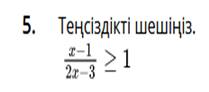
Тақырып 4. Күрделі және кері функция ұғымдары.
Анықтама.y=f(u) функциясы берілсін. Анықталу облысы u € U, ал функция мәндерінің жиыны Y болсын. Айнымалы u өз кезегінде айнымалы х-ке тәуелді функция болса, яғни u = g(x), x € X, онда y = f(g(x)) функциясы х-аргументі бойынша Х жиынында анықталғанкүрделі функция болады.
Демек, күрделі функцияның жалпы түрі: y = f(g(x)).
Егер y=f(u) функциясының u нүктесінде, ал u = g(x) функциясының х нүктесінде туындылары бар болса, онда күрделі функцияның х аргументі бойынша туындысы бар болып және ол туынды келесі y’=f’(g(x)) * g’(x)
формуласымен анықталады.
y=f(g(x)) – күрделі функция
g(x) – ішкі функция
f(t) – сыртқы функция
Күрделі функция-
екі және одан да көп функциялар композициясы
1. Кері функция
![]() түрінде берілген функция
күрделі функция деп аталады.
түрінде берілген функция
күрделі функция деп аталады.
Анықталу
облысы ![]() ,
мәндер жиыны Е болатын
,
мәндер жиыны Е болатын ![]() функциясы
берілсін. Егер
функциясы
берілсін. Егер ![]() мәніне
мәніне ![]() жалғыз
мәні сәйкес келсе анықталу облысы
жалғыз
мәні сәйкес келсе анықталу облысы ![]() ,
мәндер жиыны
,
мәндер жиыны ![]() болатын
болатын ![]() функциясы
анықталған. Осылай анықталған
функциясы
анықталған. Осылай анықталған ![]() функциясы
функциясы ![]() функциясына
кері деп аталып,
функциясына
кері деп аталып, ![]() түрінде
жазылады.
түрінде
жазылады. ![]() және
және ![]() түріндегі
функцияларды өзара кері деп аталады.
түріндегі
функцияларды өзара кері деп аталады. ![]() функциясына
кері
функциясына
кері ![]() функциясын
табу үшін х-ке қатысты
функциясын
табу үшін х-ке қатысты ![]() теңдеуін
шешу
теңдеуін
шешу
жеткілікті болады (егер мүмкін болса). Кері функция анықтамасы бойынша,
![]() функциясының
кері функциясы болады, сонда тек қана сонда егер
функциясының
кері функциясы болады, сонда тек қана сонда егер ![]() функциясы
функциясы
![]() және
және ![]() жиындарының
арасында өзара бірмәнді
жиындарының
арасында өзара бірмәнді
сәйкестік орнатса. Осыдан әрбір қатаң монотонды функцияның кері функциясы болатының шығады. Егер функция өссе (кемісе), кері функция да
өседі (кемиді).

Мысалдар
1. У1=((х6+6)2)1 =12х5(х6+6)
2. У1=((2х3-5)6)1= 36х2(2х3-5)
3.У1 = ((2х −7)8) = 16 (2х−7)7
4.У1 = ((9х+5)5)1 =45(9𝑥+5)4
1. Функциялардың берілген аралықтағы кері функцияларын табыңыздар:
a) y = 4x – 2 𝑥 ∈[−1;2]
b) 𝑦=5𝑥−1 𝑥 ∈[ 1; ∞)
c) 𝑦=(𝑥−3)2+2 𝑥 ∈[ 3; ∞)
d) 𝑦=1+ √𝑥−2 𝑥 ∈[−2;∞)
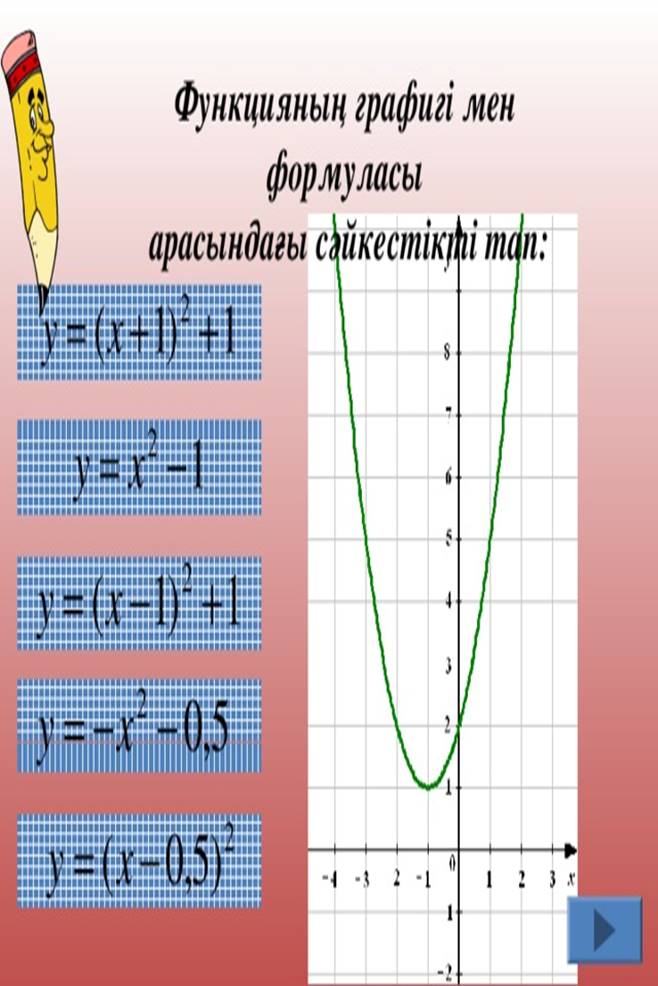
1. Берілген функциялар мен олардың кері функциялары арасындағы сәйкестікті анықтаңыз:
1. f(x) =2x+1 A. 𝑔(𝑥)=1−𝑥2
2. f(x) =1 - 2x B. 𝑔(𝑥)=𝑥−12
3.𝑓(𝑥)=1𝑥+2 𝐶.𝑔(𝑥)=1𝑥−2
4.𝑓(𝑥)=12−𝑥 𝐶. 𝑔(𝑥)=2𝑥−2
5. 𝑓(𝑥)=2𝑥+2 𝐶. 𝑔(𝑥)=2−1𝑥


Бұл тестте функция,оның қасиеттері және графигі туралы сұрақтар болады.
Бағалау шкаласы : 5 бал
Тест
1 сұрақ
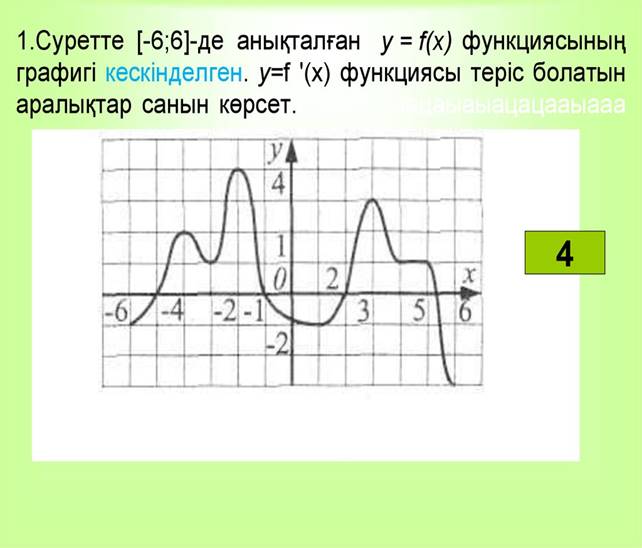
 Графигі бойынша функцияның қанша экстремум нүктесі бар екенін
анықта:
Графигі бойынша функцияның қанша экстремум нүктесі бар екенін
анықта:
Жауап нұсқалары
· 3
· 5
· 8
· 6
2 сұрақ
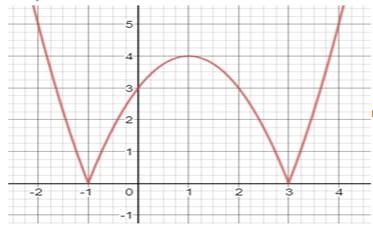
Графигі берілген функцияның экстремумдарын тап:
Жауап нұсқалары
· x max=1,x min=-1,x min=3
· y max=1,y min=-1,y min=3
· y max=0,y min=4
· y min=0,y max=4
 3
сұрақ
3
сұрақ
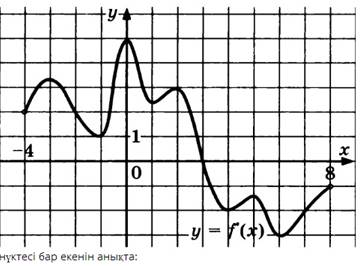
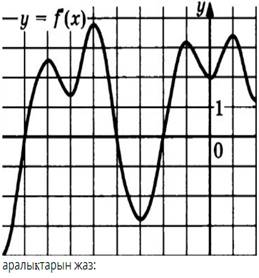
Графигі берілген функцияның өсу аралықтарын жаз:
Жауап нұсқалары
· [-1;0]
· [-3;-1]
· [-5; -3]
· [-7;-6]
· [1;+∞)
· [0;1]
· [-6;-5]
· (-∞;-7]
4 сұрақ
Жұп функцияны анықта: f(x)=x8-2x
1)f(x)=x4-x2+3x
2)f(x)=cos(x)-2IxI
3)f(x)=x4-x2+3IxI
4)f(x)=sin(x)+x
Жауап нұсқалары.
· 1
· 2
· 3
· 4
· 5
5 сұрақ
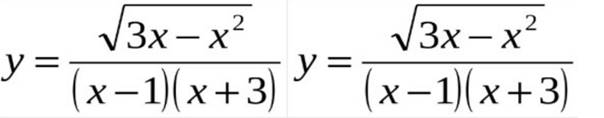 Функцияның анықталу облысын
тап:
Функцияның анықталу облысын
тап:
Жауап нұсқалары.
· (-∞;0)U(0;3)U(3;+∞)
· (-∞;-3)U(-3;0)U(0;1)U(3;+∞)
· (-∞;-3)U(-3;0)U(0;1)U(1;3)U(3;+∞)
· (-∞;-3)U(-3;0]U[0;1)U(1;3]U[3;+∞)
Әдебиеттер:
А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жұмағұлова Алгебра және анализ бастамалары: Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10-сыныбына арналған оқулық, 1-2 бөлім
А.И.Шыныбеков, Д.Ә.Шыныбеков, Р.Н.Жұмабаев Алгебра және анализ бастамалары: Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10-сыныбына арналған оқулық
А.И.Шыныбеков, Д.Ә.Шыныбеков, Р.Н.Жұмабаев Алгебра және анализ бастамалары: Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11-сыныбына арналған оқулық, 1-2 бөлім
А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жұмағұлова Алгебра және анализ бастамалары: Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11-сыныбына арналған оқулық
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.