Материал к конспекту урока по теме «Медиана», 7 класс

Материал к конспекту урока по теме «Медиана», 7 класс

Числовой набор (массив) – это конечная неупорядоченная последовательность чисел.

Среднее арифметическое – это число, равное сумме всех чисел множества, делённой на их количество.

Выбросы – это значения в наборе данных, которые значительно отличаются от остальных значений и могут быть результатом ошибок измерения или наличия редких и необычных событий. Они могут искажать статистические показатели, такие как среднее значение и стандартное отклонение, поэтому обычно их исключают из анализа данных.

Порядок действий для нахождения среднего арифметического:

Среднее арифметическое вычисляется путем сложения всех значений в наборе чисел и деления суммы на количество значений.

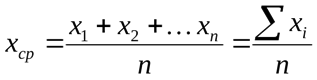, где - значения набора, n – количество элементов набора.

Пример. Пусть у нас есть следующий набор баллов за тестирование 28, 12, 28, 19, 15. Среднее арифметическое = (28 + 12 + 28 + 19 + 15) / 5 = 20,4.

Медиана – это значение признака, находящееся в середине ранжированного (упорядоченной по возрастанию или убыванию) набора чисел. Медиана делит изучаемый набор на две равные части – хотя бы у половины единиц набора значение признака не меньше медианы, и хотя бы у половины единиц - значение признака не больше медианы.

Порядок действий для нахождения медианы:

Медиана – это серединное значение в упорядоченном наборе (вариационном ряде) данных. Если количество значений нечетное, медиана – это серединное значение.

Пример 1. В наборе баллов: 28, 12, 28, 19, 15 медиана – это 19, так как после сортировки они идут в следующем порядке: 12, 15, 19, 28, 28.

Если количество значений четное, медиана – это значение равное среднему арифметическому двух серединных значений.

Пример 2. В наборе баллов 28, 12, 19, 15 медиана – это 17, так как после сортировки они идут в следующем порядке 12, 15, 19, 28 и

(15 + 19) / 2 = 17.

Для отработки знаний п8 учебника 1 част, №№ 54-57