

![]()
 1. Дан правильный
восьмиугольник. Докажите, что если его вершины последовательно соединить
отрезками через одну, то получится квадрат. В равностороннем треугольнике ABC точки M, N,
1. Дан правильный
восьмиугольник. Докажите, что если его вершины последовательно соединить
отрезками через одну, то получится квадрат. В равностороннем треугольнике ABC точки M, N,
В окружности с центром O
K — середины сторон АВ, ВС, проведены две равные хорды KL и
СА соответственно.
MN. На эти хорды опущены
Докажите, что ВMKN — ромб. перпендикуляры OH и OS. Докажите,
что OH и OS равны.
Окружности с центрами в точках M и N пересекаются в точках S и T, причём точки M и N лежат по одну сторону от прямой ST. Докажите, что прямые MN и ST перпендикулярны.
Окружности с центрами в точках M и N пересекаются в точках S и T, причём точки M и N лежат по одну сторону от прямой ST. Докажите, что прямые MN и ST перпендикулярны.
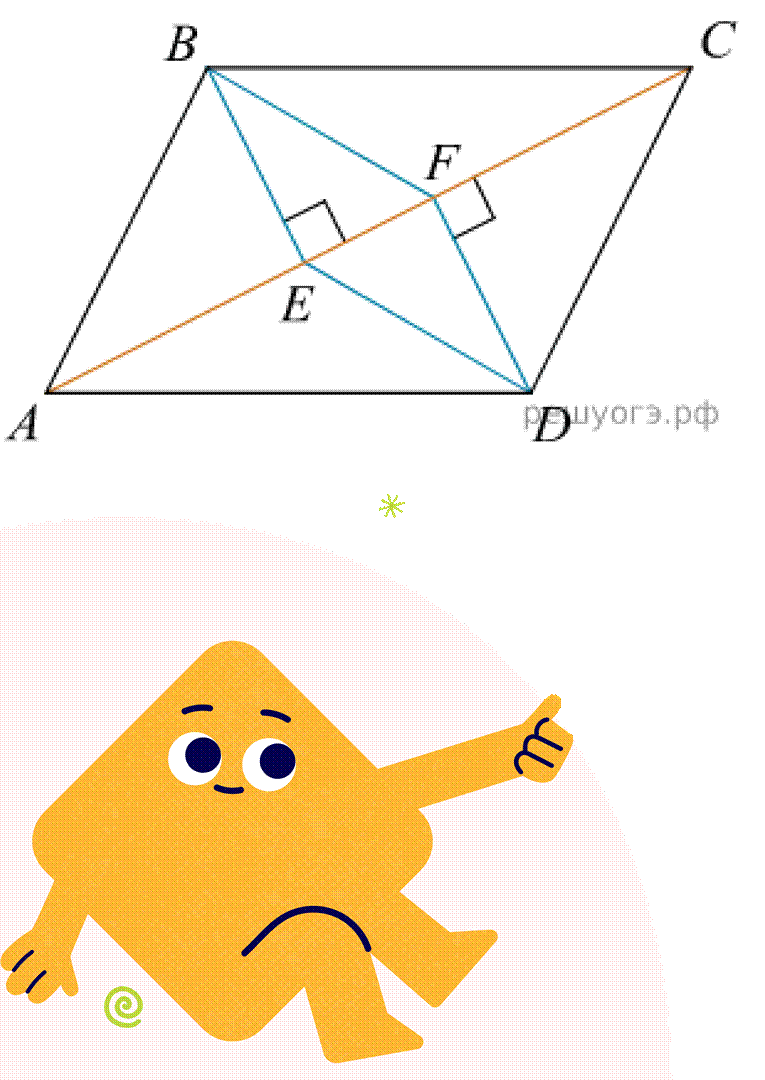 В параллелограмме АВСD проведены
перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ —
параллелограмм.
В параллелограмме АВСD проведены
перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ —
параллелограмм. ![]()
![]()
![]()
 |
 В
треугольнике ABC с
тупым углом ACB проведены
высоты AA
1 и BB
1 . Докажите,
что треугольники A 1
CB 1 и ACB подобны.
В
треугольнике ABC с
тупым углом ACB проведены
высоты AA
1 и BB
1 . Докажите,
что треугольники A 1
CB 1 и ACB подобны. 

 |


![]()
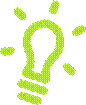 В
параллелограмме ABCD точка E
— середина стороны AB
. Известно, что EC=ED
. Докажите, что данный параллелограмм — прямоугольник.
В
параллелограмме ABCD точка E
— середина стороны AB
. Известно, что EC=ED
. Докажите, что данный параллелограмм — прямоугольник.

 Домашнее задание
Домашнее заданиеВ выпуклом четырёхугольнике ABCD углы BCA и BDA
равны. Докажите, что углы ABD и ACD также равны.
Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.
Дана равнобедренная трапеция ABCD. Точка M лежит на основании AD и равноудалена от концов другого основания.
Докажите, что M — середина основания AD.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.