Материалы для проведения экзамена по дисциплине "Математика"

Вариант 1

Часть 1

B1. Билет на автобус стоит 15 рублей. Какое максимальное число билетов

можно будет купить на 100 рублей после повышения цены билета на 20%?

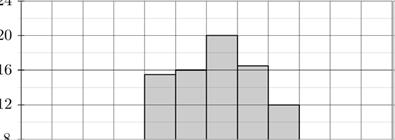
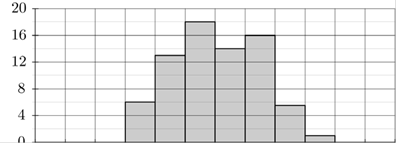
B2.  На диаграмме показана среднемесячная температура воздуха в Минске за  каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько  в 2003 году было месяцев, когда среднемесячная температура была положительной.

В3. В треугольнике ABC угол C равен 90°, АВ=20, cosA = 0,25. Найдите АС.

В4. Найдите корень уравнения:

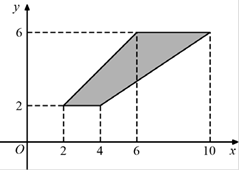
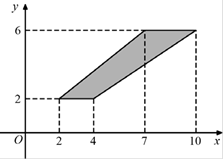
В5. Найдите площадь трапеции, изображённой на рисунке.

В6. Вычислите

В7. Решите неравенство: 

В8. Найдите cosx, если sinx = , 0 < х < .

В9. В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

В10.  Найдите первообразную функции f(x) = 5x + x², график которой проходит через точку (0;3).

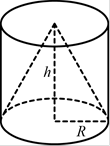
B11.  Цилиндр и конус имеют общее основание и общую высоту. Вычислите объём цилиндра, если объём конуса равен 17.

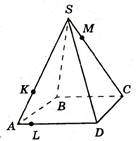
В.12 Точки K, L, M принадлежат ребрам изображенной на рисунке пирамиды. SABCD. Скопируйте рисунок и отметьте точку N на ребре CD так, чтобы отрезки KN  и LM и имели общую точку.

Часть 2

С1.  Прямоугольный треугольник , гипотенуза которого равна 17см, а один из катетов равен 8 см, вращается вокруг своего большего катета. Найдите площадь поверхности тела вращения..

С2. В правильной четырехугольной пирамиде высота равна 3 см, площадь боковой поверхности равна 80 см². Найдите объем пирамиды.

С3. Решите уравнение:    

С4.  Найдите наибольшее значение функции    f(x) = 1+8x-x² на промежутке  

Вариант 2

Часть 1

B1. Флакон шампуня стоит 190 руб. Какое наибольшее число флаконов можно купить на 1000 руб. во время распродажи, если скидка составляет 35%?

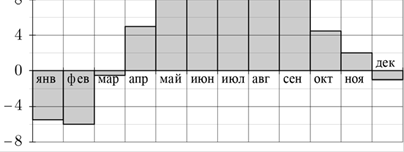
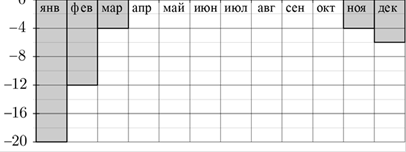
В2. На диаграмме показана среднемесячная температура воздуха в Екатеринбурге

(Свердловске) за каждый месяц 1973 года. По горизонтали указываются

месяцы, по вертикали — температура в градусах Цельсия. Определите по

диаграмме, сколько было месяцев с положительной среднемесячной

температурой.

В3. В треугольнике АВС угол С равен 90°, АВ=5, cosA=0,4. Найдите АС.

В4. Найдите корень уравнения    

В5. Найдите площадь трапеции, изображённой на рисунке.

В6. Вычислите

В7. Решите неравенство

В8. Найдите sin x, если cos x = 0,6,

В9. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.

В10. Найдите первообразную функции f(x) = 3x²-5, график которой проходит через точку (2;10).

В11. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объём

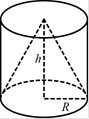цилиндра, если объём конуса равен 19.

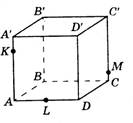
В. 12  Точки  K, L, M расположены на ребрах куба. Скопируйте рисунок и изобразите точку N, принадлежащую ребру CD, так, чтобы отрезки KN  и LM имели общую  точку.

Часть 2

С1. Квадрат  со стороной 3 см вращается вокруг своей диагонали.  Найдите  площадь поверхности тела вращения.

С2. В правильной четырехугольной пирамиде сторона основания равна 6 см, площадь боковой поверхности в два раза больше площади основания. Найдите объем пирамиды.

С3. Решите уравнение:    4^х - 3•2^х = 4

С4. Найдите наименьшее значение функции     у=2х³+3х²-12х-1 на отрезке .