Материалы к урокам физики

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Ю.Д. Корнюшкин

ОСНОВЫ СОВРЕМЕННОЙ ФИЗИКИ

(Квантовая механика, физика атомов и молекул, физика твердого тела, ядерная физика)

Учебное пособие

Санкт-Петербург

2005

Корнюшкин Ю.Д. Основы современной физики (квантовая механика, физика атомов и молекул, физика твердого тела, ядерная физика) / Учебное пособие. СПб: СПбГУ ИТМО, 2005. 326 с.

Пособие составлено в соответствии с программой по физике для технических вузов. В нем в доступной форме изложены ос- новы квантовой механики, атомной физики, физики твердого тела, физики атомного ядра. Автор, по возможности, стремился изложить основные достижения физики двадцатого века.

В основе пособия лежат лекции, прочитанные автором в тече- ние ряда лет для студентов СПбГУ ИТМО. Главное внимание в пособии уделено обсуждению физического смысла и содержа- ния основных законов природы в области микромира, а также физике твердотельного состояния.

Учебное пособие предназначено, в первую очередь, для сту- дентов младших курсов. Однако оно может быть полезным и студентам старших курсов, а также аспирантам и преподавате- лям различных специальностей.

Рецензент – Е.П. Григорьев, профессор Санкт-Петербургского государственного университета

© Санкт-Петербургский государственный университет информационных технологий, механики и оптики,

2005

© Корнюшкин Ю.Д.,

2005

Юрий Дмитриевич Корнюшкин

ОСНОВЫ СОВРЕМЕННОЙ ФИЗИКИ

(квантовая механика, физика атомов

и молекул, физика твердого тела, ядерная физика)

Учебное пособие

Редакторы К.К. Боярский, А.В. Сечкарев, С.К. Стафеев, Н.А. Ярышев

Редакционно-издательский отдел Санкт-Петербургского университета информационных технологий, механики и оптики

Лицензия № 00408 от 05.11.99.

Зав. РИО Н.Ф. Гусарова Подписано к печати 05.02.2005.

Заказ № 806.

Тираж 100 экз.

Содержание

ПРЕДИСЛОВИЕ....................................................................................................... 6

ПРЕДИСЛОВИЕ АВТОРА........................................................................................ 7

ГЛАВА 1.  ЗАКОНЫ КВАНТОВОЙ МЕХАНИКИ                                    9

           ВОЛНА ДЕ БРОЙЛЯ......................................................................................... 9

           ОПЫТ ДЭВИССОНА - ДЖЕРМЕРА............................................................... 13

           ВОЛНОВАЯ ФУНКЦИЯ.................................................................................. 19

           ФИЗИЧЕСКИЙ СМЫСЛ ВОЛНОВОЙ ФУНКЦИИ.......................................... 21

           СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ................................................... 26

           УРАВНЕНИЕ ШРЕДИНГЕРА......................................................................... 34

           ЭЛЕКТРОН В ПОТЕНЦИАЛЬНОЙ ЯМЕ......................................................... 40

                 Линейный гармонический осциллятор......................................... 41

а) Классический осциллятор....................................................................... 41

б). Квантовый осциллятор........................................................................... 44

                 Движение электрона в потенциальной яме с плоским дном...... 47

                 Движение электрона над потенциальной ямой............................. 54

                 Движение электрона над потенциальным барьером.................. 57

1.7.5 Движение электрона в направлении потенциального

барьера конечной толщины............................................................................ 60

1.7.6. Автоэлектронная эмиссия................................................................... 64

ГЛАВА 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ                                           66

            ОСНОВНЫЕ ПОНЯТИЯ.................................................................................. 66

           ОПЕРАТОР МОМЕНТА ИМПУЛЬСА............................................................. 67

           АТОМ ВОДОРОДА......................................................................................... 71

           СНЯТИЕ ВЫРОЖДЕНИЙ СОСТОЯНИЙ В АТОМЕ ВОДОРОДА................... 75

4.1. Снятие вырождения состояний по магнитному

квантовому числу.......................................................................................... 75

4.2 Снятие вырождений по орбитальному квантовому числу........ 78

           СПЕКТРАЛЬНЫЕ СЕРИИ АТОМА ВОДОРОДА............................................ 81

           СПЕКТРАЛЬНЫЕ СЕРИИ АТОМОВ ЩЕЛОЧНЫХ МЕТАЛЛОВ.................... 83

            ФИЗИЧЕСКАЯ ПРИЧИНА ВОЗНИКНОВЕНИЯ ТОНКОЙ СТРУКТУРЫ В СПЕКТРЕ АТОМОВ ЩЕЛОЧНЫХ И ЩЕЛОЧНОЗЕМЕЛЬНЫХ

ЭЛЕМЕНТОВ.................................................................................................. 89

           ЭНЕРГИЯ СПИН-ОРБИТАЛЬНОГО ВЗАИМОДЕЙСТВИЯ............................ 96

           РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ В АТОМЕ ПО СЛОЯМ

И СОСТОЯНИЯМ.......................................................................................... 100

               ДВУХАТОМНАЯ МОЛЕКУЛА.................................................................. 102

ГЛАВА 3. ОСНОВЫ ФИЗИКИ ТВЕРДОГО ТЕЛА                              114

            КЛАССИФИКАЦИЯ ТВЕРДЫХ КРИСТАЛЛИЧЕСКИХ ТЕЛ....................... 114

                 Ионные кристаллы.......................................................................... 117

                 Ковалентные кристаллы.............................................................. 118

                 Металлические кристаллы........................................................... 119

                 Молекулярные кристаллы............................................................. 120

            ОСНОВНЫЕ ОСОБЕННОСТИ КЛАССИЧЕСКОЙ И КВАНТОВОЙ СТАТИСТИКИ....................................................................... 120

           ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ФЕРМИ-ДИРАКА...................................... 125

           КВАЗИЧАСТИЦЫ В КРИСТАЛЛИЧЕСКОМ ТВЕРДОМ ТЕЛЕ.................... 131

               Фононы кристаллической решетки............................................. 131

               Квазиэлектроны кристаллической решетки............................ 137

           РАСПРЕДЕЛЕНИЕ СВОБОДНЫХ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ............. 139

           ЯВЛЕНИЕ СВЕРХПРОВОДИМОСТИ........................................................... 145

           СВОБОДНЫЕ ЭЛЕКТРОНЫ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ

ТВЕРДОГО ТЕЛА......................................................................................... 152

               Адиабатическое приближение..................................................... 152

               Приближение самосогласованного поля.................................... 153

               Приближение почти свободных электронов............................ 154

               Приближение сильной связи.......................................................... 155

           ЗОННАЯ ТЕОРИЯ ТВЕРДЫХ ТЕЛ............................................................... 156

            ЭФФЕКТИВНАЯ МАССА КВАЗИЭЛЕКТРОНА В ТВЕРДОМ ТЕЛЕ............ 161

               ДЫРОЧНАЯ ПРОВОДИМОСТЬ................................................................. 164

             ЭЛЕКТРОХИМИЧЕСКИЙ ПОТЕНЦИАЛ В СОБСТВЕННЫХ ПОЛУПРОВОДНИКАХ............................................................................... 167

               ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ......................................................... 171

               ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ................................... 175

                   Собственный полупроводник...................................................... 176

                   Примесные полупроводники........................................................ 178

               КОНТАКТ ДВУХ ПОЛУПРОВОДНИКОВ.................................................. 179

               ФИЗИЧЕСКИЕ ОСОБЕННОСТИ КОНТАКНОГО СЛОЯ

В p-n ПОЛУПРОВОДНИКЕ.......................................................................... 182

               КОНТАКТ МЕТАЛЛ - ПОЛУПРОВОДНИК................................................ 187

               СООТНОШЕНИЕ ЭЙНШТЕЙНА............................................................... 191

               ВЫПРЯМЛЯЮЩЕЕ ДЕЙСТВИЕ p-n ПЕРЕХОДА..................................... 193

               ТРАНЗИСТОРЫ......................................................................................... 199

               ВНУТРЕННИЙ ФОТОЭФФЕКТ В ПОЛУПРОВОДНИКАХ........................ 203

                   Фоторезисторы (фотосопротивления).................................. 204

                   Фотодиоды, фотоэлементы....................................................... 206

               ФИЗИЧЕСКИЕ ОСНОВЫ РАБОТЫ ЛАЗЕРОВ........................................... 211

                   Время жизни атома в возбужденном состоянии................. 211

                   Принцип детального равновесия............................................... 214

                   Основные принципы работы лазеров....................................... 217

                   Гелий -неоновый лазер................................................................... 218

                   Полупроводниковые лазеры......................................................... 221

               ЭМИССИОННЫЕ ЯВЛЕНИЯ..................................................................... 229

                   Термоэлектронная эмиссия из металлов................................. 230

                   Полевая электронная эмиссия.................................................... 236

                   Фотоэлектронная эмиссия......................................................... 237

Фотоэлектронная эмиссия из металлов                   239

Фотоэлектронная эмиссия из полупроводников     241

ГЛАВА 4.  ОСНОВЫ ФИЗИКИ АТОМНОГО ЯДРА                           242

            ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ..................................................................... 242

              Основные свойства элементарных частиц............................... 244

               Кварковая структура адронов..................................................... 247

           СТРОЕНИЕ АТОМНОГО ЯДРА................................................................... 250

           ЭНЕРГИЯ СВЯЗИ ЯДРА............................................................................... 251

           ЯДЕРНЫЕ СИЛЫ......................................................................................... 255

           СТРОЕНИЕ АТОМНЫХ ЯДЕР..................................................................... 261

               Модель жидкой капли..................................................................... 265

           ФОРМУЛА ВЕЙЦЗЕККЕРА......................................................................... 265

           МЕЗОННАЯ ТЕОРИЯ ЯДЕРНЫХ СИЛ......................................................... 268

           МОДЕЛЬ ЯДЕРНЫХ ОБОЛОЧЕК................................................................. 272

           НАПРАВЛЕННОСТЬ РАДИОАКТИВНЫХ ПРЕВРАЩЕНИЙ....................... 278

               РАДИОАКТИВНОСТЬ............................................................................... 283

                   Закон радиоактивного распада................................................. 284

                   a- распад.......................................................................................... 288

                   b- распад........................................................................................... 296

               ЯДЕРНЫЕ РЕАКЦИИ................................................................................. 299

               ЭФФЕКТИВНОЕ СЕЧЕНИЕ ЯДЕРНОЙ РЕАКЦИИ.................................... 303

               ДЕЛЕНИЕ ТЯЖЕЛЫХ ЯДЕР ПРИ ЗАХВАТЕ НЕЙТРОНА......................... 304

            ПРОДУКТЫ ДЕЛЕНИЯ УРАНА ПОД ДЕЙСТВИЕМ ТЕПЛОВЫХ НЕЙТРОНОВ............................................................................ 311

               ЦЕПНАЯ ЯДЕРНАЯ РЕАКЦИЯ.................................................................. 314

               РЕАКЦИИ СИНТЕЗА ЛЕГКИХ ЯДЕР......................................................... 319

                   Термоядерные реакции................................................................. 319

                   Термоядерные источники энергии Солнца.............................. 324

Предисловие

Автор предлагаемого учебного пособия, кандидат технических наук, доцент Юрий Дмитриевич Корнюшкин более полувека проработал на кафедре физики СПБГУ ИТМО. Все годы Великой Отечественной войны вплоть до Победы он провел на фронте, выполнял тяжелые во- енные обязанности рядового, автоматчика, артиллериста, а после войны закончил инженерно-физический факультет и аспирантуру. В течение многих лет он проводил все виды занятий, включая полный лекционный цикл по курсу общей физики, участвовал в составлении ряда учебно-методических пособий.

Ю.Д. Корнюшкиным написан и опубликован обширный цикл работ по физической электронике.

До последнего времени он проявлял неизменный интерес к совер- шенствованию учебно-лабораторного практикума, постановке новых современных лабораторных работ.

Предлагаемая читателю книга – последний труд Ю.Д. Корнюшкина, закончить который помешала его внезапная кончина в канун 80- летнего юбилея.

Сотрудники кафедры, ознакомившись с содержанием рукописи (проф. А.В. Сечкарев – гл. 1, 2; проф. С.К. Стафеев и доц. К.К. Бояр- ский – гл. 3; проф. Н.А Ярышев – гл. 4), считают, что данное учебное пособие по своему содержанию значительно превышает тот объем заключительной части лекционного курса физики, который читается в последние годы на инженерных факультетах нашего университета. Рецензенты кафедры не пытались вносить в содержание и структуру пособия существенные дополнения, о которых сказано в авторском предисловии, а ограничились лишь исправлением замеченных неточ- ностей, сохраняя авторский стиль изложения. Учтено также большин- ство замечаний, сделанных рецензентом рукописи д.ф.-м.н., профес- сором Е.Г. Григорьевым.

Считаем, что данное пособие будет полезным дополнением к имеющимся учебникам и позволит студентам младших и старших курсов расширить кругозор в области современной физики.

Зав. кафедрой физики,

д.т.н., профессор                                             С.К. Стафеев

Предисловие автора

Одна из главных задач преподавания физики в вузе состоит в том, чтобы объяснить студенту основные законы природы, развить у него навыки использования полученных знаний, а также выработать осно- вы логики физического мышления, особенностью которого является умение не только оперировать идеальными моделями изучаемого яв- ления, но и соотносить эти модели с реальной действительностью.

Физика - быстро развивающаяся наука. И то, что ранее казалось ее новыми достижениями, через некоторое время на поверку оказывается либо устаревшими, либо общепринятыми представлениями. При  этом, однако, старые достижения не становятся неверными: развитие физики лишь определяет границы их применимости.

Настоящее учебное пособие предназначено для студентов, обучаю- щихся по программе 2-го курса технического университета, но, тем не менее, некоторые его разделы могут быть полезными студентам стар- ших курсов, аспирантам и преподавателям.

В главе 1 формулируются основные законы квантовой механики в наиболее доступной для понимания студентами 2-го курса форме. В ней рассмотрено движение электрона в потенциальной яме конечной глубины. В результате полная энергия электрона оказывается завися- щей от ширины и глубины потенциальной ямы, плотность уровней полных энергий в пределах потенциальной ямы распределена нерав- номерно.

Глава 2 посвящена физике атомов и молекул. В ней, в частности, объясняется физическая причина вырождения состояний в атоме во- дорода по орбитальному и магнитному квантовым числам. При анали- зе двухатомной молекулы вводится понятие обменного взаимодейст- вия. Обсуждается физическая природа спин-орбитального взаимодей- ствия и влияния его на особенности спектров атомов щелочных ме- таллов.

В главе 3 излагаются основы физики твердого тела. Значительный акцент сделан на физике сверхпроводников 2-го рода как наиболее перспективных в настоящее время сверхпроводников. Подробно об- суждается внутренний фотоэффект в полупроводниках. Объясняются физические принципы работы фотосопротивлений, фотодиодов, фото- элементов, оптронной пары. Сформулированы физические принципы создания гетеропереходов. Объяснена физика лазерного излучения.

В главе 4 обсуждаются основы физики атомного ядра. В отличие от общепринятого подхода, изложение основ физики атомного ядра на- чинается с обзора физических свойств элементарных частиц. Теория α-распада доводится до количественного расчета энергии вылетевших из ядра α-частиц.

Следует заметить, что распределение изложения по отдельным гла- вам довольно неравномерно. Наибольший объем приходится на 3-ю главу, и это не случайно: именно этот раздел физики во второй поло- вине 20 века получил наибольшее развитие, именно в этой области были сделаны наиболее выдающие достижения и открытия.

Основой учебного пособия являлись лекции, прочитанные автором в течение многих лет в Ленинградском институте точной механики и оптики на дневном отделении. Пособие охватывает все основные раз- делы современной физики, а именно, элементы квантовой механики, физики атомов и молекул, физики твердого тела, физики атомного ядра и элементарных частиц. Автор по возможности пытался на дос- тупном для студентов уровне изложить основные идеи современной физики, объяснить явления и законы в области микромира.

Как правило, изложение ведется с использованием математического аппарата, известного студентам 2-го и старших курсов.

Автор в пособии сознательно широко использовал математику, счи- тая, что только на ее основе можно строго объяснить основные законы природы. Это, в первую очередь, относится к применению теории дифференциальных уравнений, используемых при анализе некоторых конкретных задач с целью выявления количественных физических закономерностей в изучаемых явлениях природы.

Применение доступного для студентов математического аппарата имеет несомненное достоинство, так как позволяет описать законы природы не только качественно, но и количественно. В тех же случа- ях, когда для описания физического процесса необходимо применять специальный математический аппарат, выходящий за пределы сту- денческой программы, используется лишь качественный подход с ука- занием основных идей в проводимых физических рассуждениях. Та- кой подход, в частности, осуществлен при описании явления сверх- проводимости.

Пособие называется "Основы современной физики". Оправданием такому названию является то, что в нем фактически охвачены важ- нейшие открытия в физике, начиная с 1923 года по 2000 год. Не все разделы физики в пособии в равной степени отражены достаточно подробно, некоторые из них вообще опущены. Это связано с тем, что

одни находятся в стадии интенсивного формирования, другие – из-за того, что их содержание выходит за пределы программы 2-го  курса, по которой автор составлял настоящее пособие. Автор при отборе ма- териала был ограничен объемом учебного пособия, и поэтому некото- рые важные разделы физики, такие, как явление сверхтекучести, эф- фекты Мессбауэра, Джозефсона и некоторые другие, не нашли своего отражения.

Автор надеется, что учащийся, изучивший настоящее пособие, бу- дет хорошо ознакомлен с основами современной физики, с ее дости- жениями и проблемами. Автор уверен, что знание основ современной физики в дальнейшем позволит студенту, уже находясь на старших курсах, более успешно овладевать многими специальными техниче- скими дисциплинами.

Глава 1. ЗАКОНЫ КВАНТОВОЙ МЕХАНИКИ

             Волна де Бройля

Из предыдущих разделов физики нам известно, что такие процессы природы, как тепловое и рентгеновское излучения, фотоэффект и др., хорошо объясняются на основе использования корпускулярных пред- ставлений. С другой стороны, интерференция, дифракция, поляриза- ция света объясняются на основе волновых представлений, согласно которым свет есть электромагнитные волны. Таким образом, свет, в широком понимании этого слова, представляет своеобразное сочета- ние волновых и корпускулярных свойств материи. В одних условиях эта материя наиболее четко проявляет волновые свойства, в других – корпускулярные. Одним из критериев применимости того или иного подхода является величина поперечного сечения цуга волн: если по- перечное сечение цуга волны сравнимо с размерами частиц вещества, то свет, электромагнитная волна проявляют корпускулярные свойства и электромагнитное излучение можно рассматривать как поток свето- вых частиц, если же поперечное сечение цуга волн значительно боль- ше размера частиц, то свет следует рассматривать как поток электро- магнитной волны.

Таким образом, свет как материя обладает двойственной природой. Пусть на границу раздела двух сред падает плоская электромагнит-

ная волна.

Рис. 1.1.1. Изменение скорости частицы у поверхности раздела сред без учета преобразования полей

Из рис. 1.1.1 следует, что v_1x = v_2x или

v sin i

= v sin i ;

n = c , n

= c ;

sin i 1

= v1  =  n 1 . = 1 ,

1              1           2

2              1                       2

1                        2

sin i  2     v2   n 2                  n

n = n 2 – абсо-

n 1

лютный показатель преломления, i₁, i₂ – углы падения и преломления. Применив корпускулярный подход, мы получили закон, обратный закону преломления. Таким образом, хотя для оптических явлений корпускулярный подход применим, но он дает неверный результат. Причина несоответствия корпускулярной теории опыту состоит в том, что для описания этого процесса необходим иной подход, при кото- ром учитываются взаимодействия множества световых частиц с ато- мами вещества. Математической основой описания такого процесса

является кинетическое уравнение переноса.

В 1923 г. французский ученый де Бройль высказал предположение, что двойственная природа материи должна проявляться не только у электромагнитного излучения. Он предположил, что электроны при определенных условиях должны проявлять волновые свойства. Он писал: "В оптике в течение столетия слишком пренебрегали корпус- кулярным способом рассмотрения явлений по сравнению с волновым. Не делалось ли в теории материи обратной ошибки? Не думали ли мы слишком много о картине частиц и не пренебрегали ли чрезмерно кар- тиной волн?" В 1929 г за эту работу ему была присуждена Нобелев- ская премия.

Де Бройлю было 30 лет, когда он высказал свою гипотезу о волно- вых свойствах материи и вывел формулу, с помощью которой можно вычислить длину волны, связанную с движущимся электроном. К мысли о том, что электрон должен обладать волновыми свойствами, де Бройля привели следующие факты и соображения. В природе су- ществует аналогия между геометрической оптикой и механикой. Ос- новные законы этих двух разделов физики можно сформулировать в тождественно математической форме. Это значит, что вместо того чтобы рассматривать движение заряженной частицы в электрическом

поле с потенциалом

j(r ) , можно рассматривать распространение по-

тока частиц в пространстве с абсолютным показателем n(r ) .

Заметим, что рассматриваемая аналогия в настоящее время охва- тывает все разделы физики и в ряде случаев бывает очень полезной. Покажем это на конкретном примере.

Допустим, имеется две контактирующие между собой среды. По- тенциал электрического поля в верхней среде φ₁, а потенциал в ниж-

ней среде φ₂. На границе раздела происходит постепенное изменение потенциала. Тогда напряженность электрического поля в пограничном слое можно представить в виде (см. рис. 1.1.2):

r      dj r       r

Если φ₁> φ₂ ,

E = -

dy

j = Ey j.

dj <

r      r,

0,   E ­­ j

dy

и в пределах пограничного слоя на электрон будет действовать сила

Fy = eE,

e < 0,

направленная вниз, а в направлении координатной оси 0Х сила дейст- вовать не будет, так как E_x=0. Следовательно,

F1x  = F2 x  = 0,

sin i1

sin i2

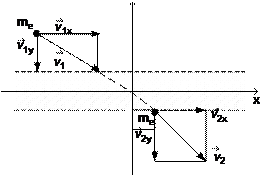y

v1x = v2 x ;

= v2 .

v1

Fy ­¯ j.

(1.1.1.)

Рис. 1.1.2. Изменение скорости частицы у поверхности раздела сред с учетом преобразования полей

Электрон, проникая в пространство с потенциалом φ₁, приобретает кинетическую энергию

m v²

k1 = e 1 = eDj1

2

Тогда в пространстве с потенциалом φ₂ его кинетическая энергия будет

Значит,

m v²

k2 = e 2 = eDj 2.

2

1

v2 ⎛ Dj2 ⎞ 2

(1.1.2)

Подставляя полученное выражение (1.1.2) в (11.1.), имеем:

1

sin i1

sin i 2

⎛        ⎞

⎜ Dj 1 ⎟

(1.1.3)

⎝        ⎠

Формула (1.1.3) является математической записью закона прелом- ления в электронной оптике.

Закон преломления в геометрической оптике формулируется в виде

n   = n 2 = sin i 1 .

(1.1.4)

1

sin i 2

Из сравнения выражений (1.1.3) и (1.1.4) можно получить относи- тельный показатель преломления в электронной оптике:

1

⎛ Dj2 ⎞ 2

(1.1.5)

n21 = ⎜ Dj ⎟

⎝     1 ⎠

В случае электромагнитных волн плоская электромагнитная волна представляет собой пучок параллельных лучей, для которых волновой фронт – плоскость, перпендикулярная направлению распространения лучей, а волновая поверхность – система параллельных поверхностей

с колебаниями векторов E и H в одной и той же фазе

r                            r     r

r          2p  r    r

E = E0 cos(wt - k x) × j ,

H = H 0 cos(wt - k x) × k ,

k = l , k = r .

Однако, если принять корпускулярную точку зрения, то плоскую электромагнитную волну можно рассматривать как поток световых частиц, перемещающихся в пространстве параллельно (рис. 1.1.3) или даже связать ее с отдельно движущимся фотоном.

Если в пространстве существует поток свободных, не взаимодей- ствующих между собой электронов (на эти электроны не действуют внешние силы), то в таком потоке электроны должны перемещаться параллельно. Эта картина верна, если пользоваться корпускулярными представлениями. Но если воспользоваться волновыми представле- ниями, т.е. применить понятие волны материи, то с таким потоком частиц можно связать некий волновой процесс, и описание движения электронов с волновой точки зрения должно быть аналогично описа- нию плоской электромагнитной волны. Следовательно, такой волно- вой процесс также можно изобразить в виде плоской волны. Поэтому де Бройль предположил, что между волновыми и корпускулярными

характеристиками электрона должна существовать точно такая же взаимосвязь, как и между соответствующими характеристиками фо- тона. И, кроме того, де Бройль предположил, что корпускулярное опи- сание движения свободного электрона должно быть подобно корпус- кулярному описанию фотона, волновое описание свободного электро- на должно быть подобно волновому описанию потока фотонов в элек- тромагнитной волне (рис. 1.1.3).

mф   c

mф   c

mф   c

фотоны

y                                                                 y

E E E

фронт                                                                                                                               x

волны

E = E0 cos(w t - k x) × j

j = j0 cos(wt - k x)

а                                                    б

Рис. 1.1.3. Модель плоской волны для фотонов (а)

и для электронов (б)

По определению импульс фотона и энергия фотона соответственно равны

Значит,

pф = mф c,

e = mф

c² = pф с,

e = hn,

ν = c .

l

p      e    hn     h             h

(1.1.6)

ф = c =  c   =  l ;    pф  = l ,

где λ – длина электромагнитной волны, h – постоянная Планка, p_ф – импульс фотона. Таким образом, уравнение (1.1.6) связывает между собой как корпускулярные, так и волновые характеристики света во- едино, а коэффициентом связи является постоянная Планка.

Де Бройль предположил, что уравнение (1.1.6) можно применять не только для фотонов, но и для электронов. А так как импульс элек- трона p_e=p=m_ev, то длина волны некоторого волнового процесса, свя- занного с движущимся электроном, будет определяться из уравнения

p = h  = m v.

l       e

Отсюда

И если

l =

mev²

h .

mev

K =         = eU £ 10 кэВ, 2

то масса электрона m_e = m₀, т.е. практически не отличается от массы покоя. Тогда в соответствии с законом сохранения энергии можем за- писать:

mev²

1

⎛ 2eU ⎞ 2

(1.1.7)

eU =

;   v = ⎜        ⎟ . 2                ⎝ me ⎠

После подстановки найденного выражения для скорости имеем

⎛ 2eU ⎞ 2

или

m⎜        ⎟

⎝  me ⎠

U 2

м = 12,3 Å, [U]=В.

Пусть U = 100 B. Тогда  λ = 0,12  нм.  Если  же  U = 10000  B,  то  λ= 0,012 нм.

Таким образом, длина волны свободного электрона, двигающегося со скоростью v, соответствует длине волны рентгеновского излучения. На это обстоятельство мы обратим внимание в дальнейшем. Такое совпадение, разумеется, носит случайный характер.

             Опыт Дэвиссона - Джермера

Любая гипотеза, как бы она ни была привлекательна и правдопо- добна, остается гипотезой до тех пор, пока она не подтвердится опы- том. Только прямые опыты, в которых отчетливо проявлялись бы вол- новые свойства частиц, могли бы подтвердить правильность идеи де Бройля.

В 1922 г. по заказу американской фирмы "Белл-телефон" Клинтон Джозеф Дэвиссон (1881–1958) и его сотрудник Кансмен изучали от- ражение электронов от поверхности металла и при этом обнаружили какие-то аномалии. В 1925 г. Дэвиссон, находясь в Европе, показал

свои графики Максу Борну, Джеймсу Франку (аспиранту Борна) в Геттингене и Дугласу Хартри в Оксфорде.

Все они признали, что аномалии на графиках свидетельствуют о проявлении волновых свойств электронов, т.е. волн де Бройля, хотя и не убедили в этом Дэвиссона. Вскоре после возвращения в Америку в экспериментальной установке Дэвиссона во время работы случилась авария: треснула вакуумная трубка, и нагретый в это время поликри- сталлический Ni под действием кислорода воздуха окислился. После восстановления установки и прокаливания образца в вакууме иссле- дования совместно с Лестером Альбертом Джермером (1896–1971) были продолжены. Вскоре выяснилось, что спектр отраженных элек- тронов имеет отчетливо выраженные интерференционные максиму- мы. В результате к концу 1927 г. они убедились в реальности сущест- вования волн материи. Но еще в 1925 г. студент М. Борна Вальтер Эльзассер, получив задание разобраться с этим явлением, предполо- жил, что аномалии на графиках Дэвиссона объясняются электронны- ми волнами де Бройля. Он послал в журнал краткую заметку, в кото- рой объяснил результаты опытов Дэвиссона и Кансмана дифракцией волн материи. Однако на эту заметку тогда никто не обратил внима- ние.

Схема экспериментальной установки Дэвиссона представлена на рис. 1.2.1.

Рис. 1.2.1. Схема установки Девиссона

Если теперь при заданном значении угла скольжения θ и полярно- го угла менять энергию первичных электронов, то график должен иметь вид, изображенный на рис.2.2.2.

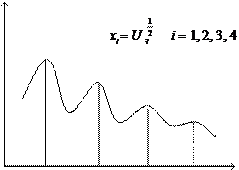I

Рис. 1.2.2. Интерференция картины электронов

1         2

Рис. 1.2.3. Модель интерференции волн в кристалле

Известно, что монокристалл Ni можно представить в виде сис- темы кристаллографических плоскостей. Если принять, что отражение волн материи происходит от кристаллографических плоскостей, то в результате интерференции волн максимум отраженной волны будет возникать в случае разности хода лучей, кратной длине волны (рис. 1.2.3). Из рис. 1.2.3 следует, что разность хода у интерферирующих лучей 1 и 2

D = 2d sin q .

Отсюда

2d sin q = ml,    m = 1, 2, 3, ... ,                 (1.2.1)

где d – межплоскостное расстояние, θ – угол скольжения. Если счи- тать, что гипотеза де Бройля правильна, то длина волны

и после подстановки в (1.2.1) получаем:

12,3 ×10^-10

12,3 ×10^-10

2d sin q = m

⎛ U 2 ⎞ 2

;

1

⎛ U3 ⎞ 2

= mc1 ,

1

⎛ U 4 ⎞ 2

c1 =

2d sin q ;

⎜     ⎟

⎝ U1 ⎠

= 2 ;

⎜     ⎟

⎝ U1 ⎠

= 3 ;

⎜     ⎟

⎝ U1 ⎠

= 4 .

Таким образом, возникновение максимумов на экспериментальных графиках следует рассматривать как результат интерференции волн неизвестной пока природы, которые связаны с движущимся электро- ном в пространстве. Значит, движение электронов в пределах кри- сталлической решетки можно рассматривать как волновой процесс.

Наличие экспериментально наблюдаемых максимумов и миниму- мов и их правдоподобное объяснение является доказательством пра- вильности гипотезы де Бройля о наличии в природе волн материи. Как оказалось впоследствии, волновыми свойствами обладают не только электроны, но и любые микрочастицы.

             Волновая функция

Итак, несомненно, поток электронов обладает и волновыми, и корпускулярными свойствами. Это значит, что двигающемуся элек- трону соответствует какой-то волновой процесс неизвестной пока природы. Де Бройль также не понимал физическую природу этого волнового процесса и поэтому предложил описать его с помощью функции, которую он назвал волновой функцией, т.е. функцией, кото- рая описывает движение частиц с волновой точки зрения. Но при этом он считал, что при таком описании должна сохраниться аналогия с описанием волнового процесса в оптике.

Мы знаем, что движение фотонов в виде пучка параллельных лу- чей описывается плоской электромагнитной волной. Следовательно, и движение свободных электронов, перемещающихся в пространстве параллельно и прямолинейно, также должно описываться в виде пло- ской волны, образованной волновой функцией.

Введение волновой функции, ее конкретный вид проще всего вы- яснить на примере использования знакомых нам явлений.

Уравнение плоской электромагнитной волны имеет вид

E = E0 cos(wt - k x),    H = H 0 cos(wt - k x).

Запишем теперь это же уравнение так, чтобы в него вошли как корпускулярные, так и волновые характеристики материи. Для этого перейдем от ω и k, характеризующих процесс с волновой точки зре- ния, к энергии кванта ε и импульсу кванта p, характеризующим тот же процесс с корпускулярной точки зрения:

w = 2pν = 2p hn =  2p e = e ;   h =   h ;

h           h       h           2p

k = 2p = 2p h  = 2p p =  p  ;

l      h  l     h        h

здесь p – импульс фотона. Тогда, заменив ω и k в уравнении плоской электромагнитной на ε и p, получим:

0           ⎜                ⎟              ₀      ⎜               ⎟

Аналогичное выражение получается, если плоскую волну выразить не через косинус, а через синус. Поэтому в общем случае эти две три- гонометрические функции можно объединить и записать уравнение плоской электромагнитной волны в более общем виде:

E = E0 e

- i (e t - p x )

h              ,

H = H0 e

- i (e t - p x )

h             .

При такой форме записи мы видим, что в уравнении плоской элек- тромагнитной волны отображаются и волновые, и корпускулярные свойства материи. Волновые свойства здесь проявляются в том, что эти уравнения записаны в виде волны, а корпускулярные свойства проявляются в том, что параметрами электромагнитной волны явля- ются энергия фотона e и импульс p фотона, причем под e здесь пони- мается полная энергия фотона или других микрочастиц, если подоб- ные рассуждения проводить для них. Если же движение фотона про- исходит в произвольном направлении, то в общем случае уравнение плоской электромагнитной волны с учетом корпускулярных свойств материи будет

E = E e h

p r                                                        p r

,    H  = H e  h                   ,

0                                                  r  0  r       r      r

E0 = const, H 0 = const, r = x i  + y j + z k .

Де Бройль в своих физических рассуждениях исходил из предвзя- той, но очень плодотворной идеи. Он считал, что законы природы и уравнения, при помощи которых описываются эти законы как с вол- новой, так и с корпускулярной точек зрения, во всех физических явле- ниях должны быть едины и поэтому должны иметь тождественный

вид. Поэтому де Бройль предложил воспользоваться аналогичным вы- ражением для описания волновых свойств электрона, только вместо векторов E и H , имеющих ясный физический смысл в случае свето- вого потока, ввести некоторую волновую функции ψ, записав с помо-

щью этой функции уравнение плоской волны:

- i (e t - px)

y = y0e h                 ,

(1.3.1)

где в случае плоской волны ψ₀ = const.

Не надо думать, что волновая функция, которая здесь была введе- на по аналогии, является характеристикой только электрона. Нет! При помощи этой функции можно также описать распространение света в пространстве как с волновой, так и с корпускулярной точек зрения. Но только физический смысл волны де Бройля будет отличаться от физи- ческого смысла электромагнитной волны. Введение волновой функ- ции ψ есть новая математическая формулировка одного из законов природы, который проявляет свое действие в микромире.

На приведенном примере мы вновь убеждаемся в том, что матема- тическая формулировка основных законов природы не выводится, а постулируется, о них догадываются. Поскольку введенная волновая функция есть закон природы, отображающий объективную реаль- ность, и поскольку ее аналитическое выражение получено путем ис- пользования аналогии, т.е. по существу по догадке, то все рассужде- ния, связанные с постулированием вида волновой функции, являются яркой иллюстрацией того, что, как правило, фундаментальные законы природы являются обобщением результатов эксперимента в виде кон- кретных аналитических формул.

Итак, на примере волновой функции ψ мы проследили все этапы открытия волновой функции для свободного электрона, мы как бы проанатомировали само открытие волновой функции, при помощи которой можно описать движение электрона с волновой точки зрения. Де Бройль считал, что уравнение (1.3.1) описывает движение сво- бодного электрона с полной энергией e = m_ec² и импульсом p = m_ev. Предположим, что в пространстве существуют такие точки и такие моменты времени, для которых фаза колебаний всегда постоянная.

Тогда для свободного электрона, у которого e = const, p = const,

e                                dx

dx     e     c²

t - px = const,

e - p     = 0;

dt

vфаз = dt = p = v

> c.

Следовательно, фазовая скорость волны де Бройля не совпадает со скоростью движения частицы, поскольку она больше скорости света в вакууме. Поэтому фазовая скорость определяет всего лишь скорость

перемещения фазы в пространстве некоторого колебательного про- цесса, описывающего движение электрона с волновой точки зрения и не больше. Это указывает на то, что волновая функция не может непо- средственно описать движение электронов в пространстве, она имеет иной более сложный физический смысл.

Итак, оказывается, что фазовая скорость свободного электрона больше скорости света в вакууме. С этой скоростью частицы в про- странстве перемещаться не могут. Если же ввести в рассмотрение та- кие гипотетические частицы, как тахионы, то окажется, что они в про- странстве могут перемещаться со скоростью больше скорости света в вакууме, но это уже будут не реально существующие в природе час- тицы. Нечто подобное имеет место в оптике, когда при рассмотрении распространения света в анизотропных средах мы вынуждены приме- нять такие понятия, как фазовая и лучевая скорости, имеющих разный физический смысл.

Иначе обстоит дело с групповой скоростью волн де Бройля. Из- вестно, что для любого волнового процесса

v       = dw =  de .

груп    dk       dp

mv²

Подставляя сюда

e = e0 +

2

и p = mv, где e₀ – энергия покоя, m

– масса, v – скорость частицы (полагаем v<<с), получим

vгруп= v.

То есть движению частицы в пространстве отвечает групповая ско- рость волны, иными словами – скорость перемещения волнового па- кета.

             Физический смысл волновой функции

Физический смысл волновой функции раскроем на примере опти- ческого явления, последовательно рассматривая его с волновой и кор- пускулярной точек зрения.

Допустим, что экран освещается пучком параллельных лучей мо- нохроматического света. Площадь поверхности экрана равна S. Пусть на поверхность экрана за 1 с попадает N квантов.

Из уравнений Максвелла для электромагнитных волн следует, что энергия электромагнитных волн в равной степени определяется вели- чиной электрической и магнитной составляющей волны. Но при энер- гетическом взаимодействии потока электромагнитной волны с веще-

ством существенную роль играет лишь ее электрическая составляю- щая. Поэтому уравнение плоской электромагнитной волны будет иметь вид

E = E0e

- i (e t - p x)

h                  .

Ф = a

1E ² = N × hn.

(1.4.1)

Разделим (2) на (1):

DФi = a i E ²

= n i hn.

(1.4.2)

DФ    a E ²   n  hn      n

=   1    0i  =    i          = i .

(1.4.3)

Ф      N hn     N hn     N

Отношение n_i/N есть отношение числа благоприятных случаев, со- стоящих в попадании n_i квантов за 1с на выделенный элемент площа- ди ∆s_i, к общему числу наблюдаемых случаев, состоящих в том, что на всю поверхность экрана S за 1с попадает N квантов. Как известно из курса  высшей  математики,   это   отношение   (строго   говоря,   при ni ® 0 ) представляет собой вероятность осуществления данного со-

N

бытия. Так как n_i << N, то это отношение обозначим

dw = ni  << 1.

N

Тогда с учетом (1.4.3) имеем

dw = a E ² ,

2     0i

a   =    a1  .

2 N hn

Отсюда видно, что квадрат напряженности электрического поля в электромагнитной волне пропорционален вероятности попадания n _i квантов за 1 с на выделенный участок поверхности ∆s_i, т.е. мы при- шли к новой физической интерпретации амплитуды напряженности электрического поля электромагнитной волны.

Теперь воспользуемся понятием волновой функции. Вспомним, как мы ввели это понятие. Это понятие нами было введено на основе ана- логии, существующей между оптическими и электрическими явле- ниями, на основе существующей аналогии движения между потоком фотонов в пучке параллельных лучей и потоком свободных электро- нов. Для фотонов можем записать:

Ei = E0ie

-  i (e t - p x )

h                  ,

y = y0e

-  i (e t - p x )

h                  .

Из  сравнения  этих  двух  функций  мы  можем  заключить,  что ψ₀

но применить не только к электронам, но и к фотонам, то примени- тельно к фотону E_0i² также аналогична ψ₀². Исходя из сказанного, мо- жем записать E_0i = a₃ψ₀ .

Тогда для фотонов имеем:

dw = a E ² = ay ² .

Но, кроме того, dω = a₄ds.

2    0i                 0

Заметим, амплитуда волновой функции ранее никак не была опре- делена, поэтому можно перейти от знака пропорциональности к знаку равенства, записав dω = ψ₀² ds.

y = yy* = y0e

-  i (e t - px)

h

× y0e

-  i (e t - p x )

h

= y².

y ² = dw.

ds

Итак, квадрат модуля волновой функции пропорционален вероят- ности попадания одного фотона на единицу площади участка облу- чаемой поверхности.

Очевидно, точно такой же физический смысл должна иметь волно- вая функция не только при описании потока фотонов, но и при описа- нии потока электронов и других микрочастиц. Подобное статистиче-

ское толкование волновой функции было предложено М. Борном (1882–1970) в 1926 г. И лишь в 1954 г. за статистическую интерпрета- цию волновой функции ему была присуждена Нобелевская премия.

Если теперь провести подобные рассуждения для пространствен- ного случая, т.е. поставить вопрос о том, какое число фотонов или других микрочастиц может находиться в микрообъеме dV в течение какого-то промежутка времени, то вероятность местонахождения микрочастицы в указанном микрообъеме dV будет определяться вы- ражением

dw = y ²dV ,

(1.1.4)

где dV = dxdydz, этот объем охватывает изменение координат от x до

x+dx, от y до y+dy, от z до z+dz.

Следовательно, в общем случае,

y ² = dw .

dV

(1.1.5)

Таким образом, |ψ|² есть плотность вероятности распределения микрочастиц в пространстве, это есть вероятность местонахождения микрочастицы в единице объема геометрического пространства. |ψ|² есть плотность вероятности.

Тогда вероятность найти микрочастицу в объеме V, как следует из

(1.4.5), равна

V

w = ò y 2 dV .                              (1.1.6)

0

И если известна ψ-функция, соответствующая данному состоянию частицы, то вероятности различных процессов определяются одно- значно, что дает возможность судить о поведении множества частиц с вероятностной точки зрения, т.е. описать их поведение методами тео- рии вероятности.

Если считать, что местонахождение микрочастицы в пространстве

- событие достоверное, т. е.  частица все время находится в объеме V,

то вероятность такого события всегда равна единице. Поэтому

V

ò y ² dV = 1.

0

(1.1.7)

Условие (1.1.7) называется условием нормировки, поскольку это условие накладывает определенные ограничения на величину ампли- туды волновой функции ψ₀ . Условие нормировки по существу есть иная форма записи закона сохранения полного числа микрочастиц в пространстве. Так как ψ=ψ(x, y, z, t), то условие нормировки должно

выполняться для любого момента времени, в противном случае оно не имеет физического смысла.

Знание волновой функции позволяет описать процессы природы вероятностным способом, а также позволяет определить средние зна- чения физических величин, например, среднее значение координаты, среднее значение скорости и др.:

При определении средних значений других физических величин часто используют операторную форму записи:

V

e  = òy^*eˆ ydV ,

0

V

òy²dV = 1.

0

0

ˆ

r

r

где e – оператор полной энергии, p – оператор импульса.

Среднее значение энергии при переходе из состояния m в состоя- ние n тогда записывается следующим образом (рис. 2):

V

ò m         n

e  =  y^* eˆy dV =  m eˆ n .

0

0

em

en

Рис. 2. Квантовый переход между двумя скачками

Допустим, микрочастица некоторое время находится в объеме

V=hs. Тогда

V

ò y ² dV < 1.

0

Это обстоятельство следует учитывать, например, при определе- нии вероятности взаимодействия электронов с веществом в процессе облучения вещества потоком электронов. Допустим, облучаемое ве- щество представляет собой металлическую пленку.

Рис. 1.4.2. Модель облучения пленки электроном

Объем облучаемой пленки   изображен на   рис. 1.4.2. А так как часть потока электронов проходит через пленку, то

V1

ò y ² dV < 1.

0

Следовательно, условие нормировки для волновой функции в этом конкретном случае должно иметь вид:

0

ò y1

-¥

h

0

¥

2 dx + ò

h

y ²dx = 1.

⎛ h *

⎞    ⎛ h

2 ⎞ .

e  = ⎜òy eˆy ⎟

⎜ò y

dx ⎟

⎜

⎝ 0

Обобщим сказанное.

⎟     ⎜               ⎟

⎠    ⎝ 0                  ⎠

1.  Волновая функция сама по себе не выражает физического смыс- ла, физический смысл имеет лишь ее квадрат модуля – он равен плот- ности вероятности местонахождения микрочастицы в единице объема геометрического пространства в пределах выделенного микрообъема dV .

2.   В квантовой механике параметры состояния микрочастицы, на-

пример,  e, p , определяются вероятностным способом, точное  значе-

ние полной энергии и импульса, а также других параметров опреде- лить невозможно, точно можно определить лишь их средние значения.

             Соотношения неопределенностей

Итак, мы видели, что свет можно рассматривать и как поток свето- вых частиц, фотонов, и как электромагнитную волну. То же самое можно сказать и об электронах и других микрочастицах. Например, в

опыте по отражению от монокристалла Ni поток электронов проявля- ет волновые свойства; однако во всех типах электроннолучевых тру- бок, например, в кинескопах телевизоров, поток электронов проявляет корпускулярные свойства, ведет себя как поток отрицательно заря- женных частиц. Подчеркнем еще раз, что подобная двойственность имеет место и у других микрочастиц, а именно, всегда в природе имеются явления, в которых частицы проявляют волновые свойства, и имеются явления, в которых эти же частицы проявляют корпускуляр- ные свойства.

Из анализа многочисленных опытов с микрочастицами с учетом волновых и корпускулярных свойств вытекает принцип неопределен- ности Гейзенберга, который, в сущности, представляет один из фун- даментальных законов природы в микромире. С одной стороны, этот принцип имеет большое философское значение, а с другой – он нахо- дит практическое применение при выполнении некоторых конкретных расчетов. Физическая причина наличия этого закона заключается в двойственной природе материи.

Открытие закона соотношения неопределенностей связано с име- нем Вернера Гейзенберга. Весной 1925 г. по приглашению Н. Бора из города Геттинген (Германия) в город Копенгаген прибыл В. Гейзен- берг. Там он сразу попал в обстановку научных споров, в среду лю- дей, для которых физика была главным делом их жизни. Основной вопрос, который обсуждал Гейзенберг, состоял в следующем: почему в атоме электрон не подчиняется законам электродинамики, почему в процессе движения электрон не падает на ядро и даже не излучает, если атом не возбужден? В конце концов, после многих раздумий и обсуждений со своими коллегами по работе он пришел к выводу, что понятие траектории электрона в атоме не имеет физического смысла, оно к электрону в атоме неприменимо.

Рассмотрим на примере наиболее понятных нам световых явлений физическую причину возникновения соотношения неопределенности.

Пусть в пространстве на плоский экран I со щелью падает пучок параллельных лучей. После экрана поместим линзу, в фокальной плоскости которой расположен другой экран (рис. 1.5.1).

Тогда, как мы знаем, на втором экране будет возникать интерфе- ренционная картина, соответствующая дифракции от одной щели. Дифракционная картина будет особенно четко видна, если ширина входной щели сравнима с длиной волны света.

Условие минимума в случае дифракции от одной щели

a sin j = kl,

где a – ширина щели, k = 1, 2, 3, . . . , l – длина волны,  Тогда угловая ширина дифракционного максимума

k < a / l .

Dj =

l

a cos j

, Dk = 1.

И если

a >> l , то

Dj << 1 , если

a << l , то

Dj > 90° , и дифракция

как в первом, так и во втором случаях наблюдаться не будет. Значит, для наблюдения четкой дифракционной картины необходимо, чтобы  a » l . Это обстоятельство мы используем в дальнейшем, когда будем более подробно рассматривать физическую причину возникновения соотношений неопределенностей.

a

II

Рис. 1.5.1. Возможная схема наблюдения интерференции волн при рассеянии на щели

Если к анализу результата опыта применить корпускулярный под- ход, то можно считать, что после прохождения через щель поток све- товых частиц, фотонов, отклоняется от первоначального направления на величину угла дифракции j . Причину такого отклонения можно

видеть во взаимодействии фотонов с веществом экрана I и возникаю- щем в результате этого рассеянии.

Положение одного фотона в потоке световых частиц в направлении оси Оx можно определить лишь с точностью, равной ширине щели a . Таким образом, неточность в определении координаты x любого из падающих фотонов будет Dx = a , поскольку в нашем распоряжении нет приборов, при помощи которых без нарушения условий исходного

опыта можно более точно определить координату фотона x. Наряду с этим существует еще и неопределенность положения фотона в преде- лах дифракционного максимума, который образован потоком рассе- янных фотонов. Вероятность углового распределения дифрагирован- ных фотонов не одинакова для различных углов дифракции: имеются направления, в которых фотоны отклоняются с большей вероятно- стью, и имеются направления, в которых фотоны практически не от- клоняются, т.е. вероятность их дифракции в этом направлении прак- тически равна нулю. Этим и объясняется наличие на экране II участ- ков с максимальной и минимальной освещенностями. Стало быть, не- определенность в определении направлении движения фотона обу- словлена конечной шириной максимума, величину которого обозна- чим Dj .

Итак, фотон в пространстве летит где-то в пределах угла

Dj , но

где именно – мы не знаем, у нас нет способа, при помощи которого можно уточнить положение фотона без нарушения условий исходного опыта. Стало быть, неопределенность углового положения фотона бу- дет равна Dj .

Фотон распространяется со скоростью света  c . Масса покоя фото-

на  m0ф = 0 , это означает, что в природе нет такой системы отсчета,  в

Заметим, что понятие релятивистской массы не является общепри- нятым. Однако "безмассовость" фотона не противоречит наличию у

него импульса

pф = e / c

Импульс фотона ось Ох будет равна

p = mфc , а проекция импульса на координатную

px = mфcx .

Тогда неточность в определении проекции импульса на ось Ох бу- дет равна

Dpx = mфDcx .

Из рис. 1.5.1 видно, что cx = c sin j, Dcx = c cosjDj , поэтому

Dp  = m c cos jDj = h cos jDj .

x             ф                                   l

Таким образом, угловой неопределенности движения фотона Dj

соответствует неопределенность величины проекции импульса Dpx .

Составим теперь произведение

Dp  Dx = h cos jDj × a = h a cosjDj .                   (1.5.1)

x                l                    l

До сих пор мы использовали корпускулярный подход к объясне- нию явления дифракции от одной щели. Применим теперь волновые представления о свете.

Известно, что условие минимума дифракции от одной щели имеет вид:

a sin j = kl,     k = 1,2,3,... < a / l .

Тогда разность углов между двумя соседними минимумами, кото- рая, собственно, и определяет угловую ширину максимума, может быть найдена из выражения:

a cosjDj = lDk = l,

и после подстановки в (1.5.1) получаем

k = 1,

DpxDx = h .                                 (1.5.2)

Из (1.5.2) следует: чем точнее задана координата фотона, т.е. чем меньше ∆x, чем меньше ширина входной щели a , тем менее точно

можно определить проекцию импульса

Dpx . И наоборот, чем точнее

известна проекция импульса, т.е. чем меньше угловая ширина макси- мума, тем менее точно может быть определена координата микрочас- тицы. Это предельная точность определения координаты, ее величина не зависит от особенностей постановки опыта, так как она вытекает из закона природы.

Полученное в результате проведенных рассуждений уравнение (1.5.2) соответствует идеальному случаю, когда измерение отдельных параметров движения микрочастицы проводилось без учета ошибок эксперимента и побочных дифракционных механизмов. На самом деле

погрешность опыта всегда увеличивает как

Dpx , так и

Dx . Поэтому

уравнение (1.5.2) следует заменить неравенством

DpxDx > h .                                 (1.5.3)

Далее, можно показать, что для направления вдоль оси Оy

Rl³

Dpy Dy = a4 cos j h,

где R – радиус дуги окружности экрана II . Но

a » l,cosj » 1, R >> a,

Поэтому

DpyDy > h .                                 (1.5.4)

Итак, в общем случае с учетом (1.5.3) и (1.5.4) имеем:

DpxDx > h ,

DpyDy > h ,                                 (1.5.5)

DpzDz > h .

Система неравенств (1.5.5) и представляет собой соотношения не- определенностей Гейзенберга. Мы получили их на примере дифрак- ции света, однако они выполняются для любых микрочастиц. Соот- ношения неопределенностей, записанные в виде системы неравенств (1.5.5), выполняются только для проекций импульсов и координат на одноименные координатные оси. Поэтому для проекций на разно- именные координатные оси правая часть неравенств (1.5.5), в частно- сти, может быть равна нулю, например,

DpxDy ³ 0, DpzDx ³ 0.

В этом случае проекцию импульса и координату вдоль разноимен- ных направлений в мысленном опыте можно определить одновремен- но с любой точностью. Так, можно совершенно точно определить и

проекцию импульса на ось Оx и координату y. В этом случае

Dy = 0 .

Dpx = 0 ,

Из системы неравенств (1.5.5) для проекций импульса и радиуса вектора на соответствующие координатные оси можно получить еще одно неравенство, связывающее между собой неопределенность вели- чины полной энергии микрочастицы с неопределенностью момента времени, когда частица имеет указанную полную энергию. Покажем это на примере фотона.

Пусть r есть направление, вдоль которого фотон движется со скоро- стью c . Для направления r запишем соотношение неопределенности:

Энергия фотона

DpDr > h, DpDr > h.

eф = mфc² = pc.

(1.5.6)

Импульс и координата фотона в момент времени t :

p = e , r = ct.

c

Тогда неопределенность значения импульса и неопределенность значения координаты фотона соответственно равны

Dp = De , Dr = cDt.

c

и после подстановки найденных значений в (1.5.6) получаем

DeDt > h .                                     (1.5.7)

Установленное неравенство (1.5.7) справедливо не только для фо- тонов, но и для иных микрочастиц.

Физический смысл неравенства (1.5.7) следующий: чем точнее из- вестен момент времени, когда была определена энергия микрочасти- цы, тем менее точно может быть определена ее полная энергия, и на- оборот. А применительно к свойствам самой системы его можно сформулировать так: чем меньше длительность некоторого энергети- ческого состояния системы, тем больше неопределенность в знании ее полной энергии.

Так как

px = mvx ,

то

Du  Dx > h .                                 (1.5.8)

x                m

Неравенство (1.5.8) позволяет установить границу применения классической и квантовой механик. Так, если координата микрочас-

тицы определяется настолько  точно,  что неопределенность  Dx ее по-

ложения в пространстве меньше характерного линейного размера час- тицы, то при анализе ее движения можно применять корпускулярный подход, если же эта неопределенность больше ее характерного разме- ра, то для описания движения необходимо использовать волновую функцию. (Характерным размером может быть, например, размер атома или молекулы).

Допустим, нам известен способ, с помощью которого можно опре-

делить скорость электрона в атоме с точностью

Dvx = 1мм/с. Тогда из

(1.5.8) следует, что

Dx » 0,7м. В этом случае

Dx >> R, где R – радиус

ядра атома. Такой электрон в процессе движения проявляет только волновые свойства. Если же эта скорость определена, допустим, в ки- нескопе телевизора, то электрон следует рассматривать как частицу.

Таким образом, движение электрона в атоме, в кристаллической решетке твердого тела может быть описано с помощью волновой функции, его положение в пространстве определяется величиной плотности вероятности.

Соотношение неопределенностей не отрицает возможность одно- временного определения координаты и импульса микрочастицы, их одновременное измерение возможно лишь с определенной точностью. В этом утверждении заключается отказ от некоторых представлений, укоренившихся в физике того времени. Так, в классической физике

широко пользуются понятием траектории движения материальной точки, траектории движения частицы, причем под траекторией пони- мается зависимость координаты, определяющей положение матери- альной точки в пространстве, от времени. Знание траектории предпо- лагает знание с любой точностью и координаты, и скорости (коорди- наты и импульса). В классической механике координата и скорость материальной точки в любой момент времени в принципе могут быть определены одновременно с любой точностью, это значит, что движе- ние материальной точки, движение центра масс в пространстве проис- ходит по определенной траектории. В квантовой механике одновре- менное абсолютно точное определение координаты и импульса мик- рочастицы в принципе невозможно. Поэтому понятие траектории движения отсутствует, оно не имеет физического смысла. Мы, конеч- но, можем указать путь, пройденный электроном, но тогда ничего не можем сказать о том, в какой момент времени электрон будет зани- мать то или иное положение в пространстве. В классической механике всегда имеется возможность однозначно предсказать будущее по прошедшему. В квантовой механике однозначность предсказания за- меняется вероятностью предсказания.

Из соотношений неопределенности вытекает принцип дополни- тельности. Он был сформулирован Н. Бором в виде следующего ут- верждения: координату и импульс микрочастицы нельзя абсолютно точно измерить не только одновременно, но и с помощью одного и того же прибора.

В самом деле, чтобы измерить импульс атома и при этом не очень сильно его изменить в результате воздействия на атом самого прибо- ра, необходим очень легкий подвижный датчик, способный переме- щаться вместе с атомом в процессе измерения. Но такая подвижность приведет к тому, что его положение в пространстве окажется весьма неопределенным. Для измерения координаты необходим прибор с очень большой массой датчика. Поэтому при попадании частицы в такой датчик положение датчика в пространстве меняться не будет. Таким образом, в природе всегда существуют две сопряженные физи- ческие величины, одновременное измерение которых в принципе не- возможно. Такими сопряженными величинами, в частности, являются координата и импульс частицы, потенциальная и кинетическая энер- гии и т.д. Гносеологическая причина несовместимости дополнитель- ных понятий заключается в двойственной природе материи. Этот за- кон является универсальным и охватывает все без исключения явле- ния природы.

             Уравнение Шредингера

Уравнение Шредингера является основным законом квантовой ме- ханики, его роль является такой же, какую второй закон Ньютона иг- рает в классической механике.

Эрвин Шредингер (1887–1961) в 1911 г. окончил Венский универ- ситет. В 1925 г. он стал профессором Цюрихского университета. Шредингер знал, что в природе существует оптико-механическая ана- логия, которую впервые установил Гельмгольц. Но Гельмгольц дока- зал ее лишь для геометрической оптики, в которой не учитываются волновые свойства света. Шредингер же предположил, что оптико- механическая аналогия сохраняется и в волновой оптике. Это значит, что любое движение частиц можно рассматривать как распростране- ние некоторой волны.

Квантовая механика – это раздел физики, описывающий движение микрочастиц в пространстве с учетом волновых и корпускулярных свойств материи. Квантовая механика рассматривает движение только тех объектов, которые в процессе движения проявляют волновые свойства. Поэтому квантовая механика движение макротел вообще не описывает. Критерий, с помощью которого можно указать границу применимости квантовой механики, определяют соотношения неоп- ределенностей.

Если

Dx ³ z

или

Dvx ³ vx , где z – характерный размер частицы, то

для решения задачи следует применять квантовую механику. Если же

Dx << z

или

Dvx << vx , то движение микрочастицы можно рассматри-

вать без учета ее волновых свойств, и следует применять классиче- скую механику.

Слово "механика" в термине "квантовая механика" как бы подчер- кивает, что эта наука изучает законы движения микрочастиц, а не их природу. Подобно тому, как классическая механика занимается изу- чением движения объектов, не вдаваясь в объяснение природы этих объектов, так и квантовая механика объясняет движение электронов вокруг ядер атомов на основе тех и только тех свойств ядер и электро- нов, которые важны для решения данной конкретной задачи.

Теоретическое объяснение законов теплового излучения, явления фотоэффекта, природы и свойств рентгеновских лучей, гипотеза де Бройля о волнах материи – все это были важнейшие этапы в развитии теоретических основ физики атома, молекул, твердого тела. Однако эти результаты явились лишь предварительным этапами при обосно- вании уравнения, описывающего движение электрона с учетом его

двойственной природы – волновой и корпускулярной. Решающий шаг в этом направлении сделал Шредингер в 1926 г., когда получил урав- нение, с помощью которого оказалось возможным описать движение электрона и других микрочастиц с учетом волновых и корпускуляр- ных свойств. Это уравнение отображает один из основных законов природы в области микромира. И подобно тому, как все основные за- коны природы не выводятся, а постулируются, устанавливаются по догадке, так и это уравнение не выводится, а постулируется, устанав- ливается на основе физической аналогии с использованием некоторой доли физической интуиции.

В физике до сих пор мы знали два закона природы, отображающих корпускулярные и волновые свойства материи.

1.  Второй закон Ньютона:

dt 2

Решением уравнения (1.6.1) является уравнение траектории мате- риальной точки в пространстве. Ограничимся пока одномерным дви- жением вдоль координаты x.

2.  Волновое уравнение для напряженности электрического поля:

¶2E =

¶x2

1  ¶2E .                           (1.6.2)

Решением уравнения (1.6.2) является уравнение электромагнитной волны

(1.6.3)

0                                           0        ⎢⎣                    h              ⎥⎦

Если теперь сравнивать между собой уравнения (1.6.1) и (1.6.2), то уравнение Шредингера является как бы промежуточным уравнением, в котором учтены и волновые, и корпускулярные свойства микрочас- тиц, оно играет точно такую же роль, какую в классической играет второй закон Ньютона, а в электродинамике – волновое уравнение.

Отметим, что в квантовой механике понятия силы, кинетической энергии, траектории не используются, так как здесь они не имеют фи- зического смысла. Объясняется это тем, что наличие силы позволяет из (1.6.1) определить траекторию движения микрочастицы. Но само понятие траектории в квантовой механике отсутствует, поэтому должно отсутствовать и понятие силы.

Рассмотрим теперь те соображения, которые могут привести к ус- тановлению уравнения Шредингера. Наши рассуждения проведем на примере свободного электрона. Как и раньше, будем исходить из того,

что волновые свойства электрона описываются волновой функцией y в виде плоской волны, введенной по аналогии с плоской электромаг- нитной волной (3).

Волновая функция свободного электрона по своей структуре по-

добна уравнению плоской электромагнитной волны, поэтому Шре- дингер предположил, что в природе должно существовать такое вол- новое уравнение, решением которого является волновая функция y :

¶²y =

¶x²

1  ¶2y ,                             (1.6.4)

где vф – фазовая скорость волны, описывающая движение свободного электрона с вероятностной точки зрения.

Таким образом, Шредингер, как и де Бройль, при формулировке

основного уравнения квантовой механики использовал метод анало- гии. Так как исходное уравнение (1.6.4) является волновым, то и сама квантовая механика также еще называется волновой механикой.

Однако уравнение (1.6.4) не является окончательным, а представ- ляет лишь некоторый промежуточный результат в процессе формули- ровки основного уравнения, поскольку в записанном виде это уравне- ние характеризует движение микрочастицы лишь с волновой точки зрения.

Учтем теперь ее корпускулярные свойства. Ранее мы нашли выра- жение для фазовой скорости волновой функции, описывающей дви- жение свободного электрона в пространстве:

v   = dx  =  e ,

ф     dt       p

Здесь ε – полная энергия электрона, p – импульс электрона. Вол- новая функция свободного электрона

-  i (et - px)

Поэтому

¶²y

y = y0e h

p2 ⎛    e2

.

⎞       p2

.                    (1.6.5)

⎜-

⎝ h2

y⎟ = -     y

Кинетическая энергия свободного электрона

p2

K =

2m

или

p2 = 2mK.

Подставим полученное выражение для квадрата импульса в (1.6.5):

¶²y = - 2m

(1.6.6)

¶x²

h Ky.

Уравнение (1.6.6) справедливо лишь для частного случая движения свободного электрона. Попробуем теперь уравнение (1.6.6) видоизме- нить так, чтобы оно было справедливым не только для свободного электрона, но и для электрона в поле других консервативных сил. В этом случае кинетическая энергия электрона

K = e - U (x),

где U (x) – потенциальная энергия электрона.

Следовательно, в общем случае,

p² = 2mK = 2m(e - U (x)).

Подставим найденное выражение в (1.6.6):

(1.6.7)

или

¶x²

U (x)

h2

)y =

.                         (1.6.8)

¶x²     h²

U (x)        0

Уравнение 1.6.8) и есть основное уравнение квантовой механики для микрочастицы в поле внешних консервативных сил, причем в случае свободного электрона потенциальная энергия электрона U = 0 . Так как в уравнение (1.6.8) время явным образом не входит, то его решение будет одним и тем же для любого момента времени. Поэтому

уравнение (1.6.8) называется стационарным уравнением Шредингера.

При выводе уравнения Шредингера была допущена физическая неточность: в (1.6.7) кинетическая энергия K была выражена через потенциальную энергию U, что противоречит соотношению неопре- деленности. Действительно, из физического смысла уравнения (1.6.7) следует, что в одном и том же опыте одновременно известны две фи- зически сопряженные величины – кинетическая и потенциальная энергии, т.е. в одном и том же опыте можно определить и точное зна- чение импульса, и точное значение координаты, что в принципе не- возможно. Единственным оправданием для Шредингера является то, что при составлении своего уравнения Шредингер не знал закона – соотношения неопределенности, этот закон был опубликован позднее. В общем случае, для реального пространства трех измерений, ста-

Dy + 2m (e -

h2

r )       ,                         (1.6.9)

где D – оператор Лапласа,

D =

¶2

¶x2

+  ¶2

¶y2

¶2

+ ¶z2 .

Перейдем к формулировке нестационарного уравнения Шрединге- ра. Так как волновая функция свободного электрона

- i (et - px)

y = y0e h                 ,

или

¶y = -

¶t

h ey0e

- i (et - px)

h

= - i ey

h

Из (1.6.9) находим εψ :

ih ¶y = ey.

¶t

(1.6.10)

ey = - h2 Dy +

2m

Тогда с учетом (1.6.10) имеем:

r

U (r )y

¶ψ       h²              r

(1.6.11)

¶t        2m ψ

U (r )ψ,

Уравнение (1.6.11) – нестационарное уравнение Шредингера. За- пишем его в иной форме:

¶y    ⎛   h²            r ⎞

(1.6.12)

ih ¶t

= ⎜-     D + U (r ) ⎟y.

2m

⎝                      ⎠

В квантовой механике каждой физической величине соответствует свой оператор. При этом для операторов физических величин в кван- товой механике обычно сохраняются соотношения, характерные для самих величин в классической механике. В уравнении (1.6.12) выра- жение в круглых скобках есть математическая операция, она называ- ется оператором Гамильтона:

Hˆ  = -

h2 D + uˆ

(1.6.13)

уравнение Шредингера в операторной форме записи:

ih¶y = Hˆy.

¶t

(1.6.14)

Из (1.6.10) и (1.6.14) получаем стационарное уравнение Шредин- гера в операторной форме записи:

Hˆy = ey,

(1.6.15)

где e – собственное значение, ψ – собственная функция оператора H .

¶y =

¶x

то

h pxy0e

- i (et - px)

h

= h pxy,